注重有效生成，培养数学能力

江苏省睢宁县第二中学 张新尚

注重有效生成，培养数学能力

江苏省睢宁县第二中学 张新尚

教学过程是师生交往、互动的过程，课堂教学不应当是一个封闭系统，也不应拘泥于预先设定的固定不变的模式，要鼓励学生在互动中大胆超越和即兴创造，针对教学实际进行灵活调整，追求动态生成，让学生的思维在生成中有效激活、提高，在生成中提高探究能力，从而让数学课堂在预设与生成的融合中焕发生命活力。下面笔者结合在课堂教学中的体验谈谈一点认识和体会。

一、思维能力在课堂生成中激活

课堂教学中，充分利用生成，找准时机，用恰当的引问、追问，适当的点拨，能够有效地激活学生的思维，点燃思维的火花。

【案例1】 “中点四边形”的课堂教学片段。

这是发生在笔者执教的初三（1）班一个常态下的教学课的真实场景，学生在探索中点四边形的过程中意外生成的问题打乱了笔者的教学预设。

师：刚才我们研究了对于一个任意四边形，顺次连接四边中点得到的四边形一定是平行四边形，我们把这个平行四边形称之为中点四边形。你还能提出一个什么样的特殊四边形，让同学们来研究它的中点四边形的形状呢？

生1（李佳慧）：顺次连接梯形的中点，得到的四边形是什么形状？（我的预设是学生会先提出：顺次连接平行四边形的中点得到的四边形是什么形状，然后再提出矩形、菱形、正方形的情况）

师：此“李佳慧问题”，由谁来解决？

生众（笑）：李佳慧回答。

师：难道只有李佳慧会解决？

学生们开始动手画图探索，我预想学生会说梯形的中点四边形是平行四边形，结果学生生成了3种答案。

生2认为是菱形，生3认为是平行四边形（正如我所愿），生4认为是矩形，其实学生都是根据画图猜想的，只不过生3画了一个一般的梯形，生2正好画了一个等腰梯形，生4无意中画了一条对角线互相垂直的梯形。

此时我没有马上充当裁判员的角色，而是顺势抛给了同学们一个问题：这三位同学的答案怎么不一样呢？你同意谁的结论？为什么？

众生齐说：生3，因为梯形本身就是四边形。

师追问：那生2说是菱形，可能吗？

学生们思考片刻后开始了交流探索。

生5：我们小组通过研究发现，只要梯形的对角线相等，得到的中点四边形就是菱形。

师追问：此时这是什么梯形？

生众：等腰梯形。

师追问：生4说是矩形，有可能吗？

部分学生：有可能。

师：什么情况下？

生6：只要对角线互相垂直。

这时生7又冒出了一个结论：我认为梯形的中点四边形还有可能是正方形，满足的条件是此梯形的对角线相互垂直且相等。

此时，笔者的内心感到非常欣慰，课堂上学生的思维已被成功激活了。

在课堂上，教师面对的是一群存在着不同差异的孩子，他们有着不同生活经历，有着自己的想法，也正因为如此，课堂才有着不断的变化、丰富多彩的“意外”。因此教师要适应这种变化，及时处理课堂上的生成，有效激发学生的思维，课堂教学效率才是高效的。虽然这样的过程（或场面）有时有点复杂，但精彩的生成也会伴随其中，这种生成说不定就是本课最大的亮点。

二、思维能力在课堂生成中培养

学生学习是一个生动活泼的、主动的和富有个性的过程，除接受学习外，动手实践、自主探索与合作交流也是数学学习的重要方式。课堂上的数学探究活动是自主探索、合作交流的过程，也是一个师生互动、生生互动、不断生成的过程，更是培养学生思维能力的过程。因此，在探究活动中，教师应随时关注学生活动中的生成，做好组织者、引导者的角色，合理利用生成使探究得以继续并不断深化。

【案例2 】 “全等三角形的判定条件” 课堂教学片段。

师：通过刚才的学习，我们已经知道用“边角边”可以判定两个三角形全等。当这里的角不是两边的夹角，而是其中一边的对角时，两个三角形还是全等的吗？

学生开始在自己的作业纸上画图、尝试，并与同桌交流。

很快大家纷纷表示这种方法不能判定两个三角形全等，突然有一学生大声道：是全等的！

师：你说说看。

生1：我是利用我作业本的拐角来画的（如图1）， 让AC=DF，AB=DE，这样画了几次都是全等的。

师：是吗？我们都来利用作业本的拐角来试试，好不好？学生通过画图、剪拼验证，发现所画的两个三角形还真是全等的。

师：那是不是说这种方法可以判断两个三角形全等？

图1

生2：我觉得不能，刚才画出来的都是直角三角形，只能说明在直角三角形中是成立的，而我画的是一个钝角三角形，一个锐角三角形，满足刚才的条件，但它们不是全等的。

师：不错，我们这样画得到的确实都是直角三角形，那至少我们可以说有两边和其中一边的对角对应相等的两个直角三角形全等。我们不妨顺着这个思路大胆想下去，如果两个三角形都是锐角三角形，或者都是钝角三角形，“边边角”还能说明全等吗？学生继续操作，发现结论都是成立的。

生3：我知道了，如果是同类的两个三角形满足“边边角”，就能判定它们是全等的。

师：对。如果没有指明两个三角形是哪类三角形，就不能用“边边角”说明三角形全等了。

在这个案例中，本来按照教师的教学预设，只需让学生动手得到用“边边角”可以画出两个不全等的三角形，从而得到不能用“边边角”来判断两个三角形全等即可。但是学生1的“不按套路”操作改变了教师对探索的预设——得到了全等三角形！教师及时抓住了这个宝贵的生成，决定调整原来的预设，非常自然地让学生探索在什么情况下是成立的，在什么情况下是不成立的，使得课堂的探索有了深度，学生对三角形全等的判定也有了更深刻的认识。

三、探究能力在生成中提高

课堂上的生成是丰富多彩的，而学生在解题过程中的生成又是教师常常遇到的，如果教师能够认识到这种生成的价值，并充分利用它来加强对学生思维的培养，往往可以起到良好的效果。在解题教学中，教师若给学生创建生成的空间和时间，并努力利用生成促进新的生成，必然会让学生在这一个个精彩的生成中充分张扬个性、发展思维。

【案例3】 题目：如图2，边长为4的正方形ABCD中，点E是边AB上的任意一点，以BE为边在正方形的外部再作一个正方形EFGB，连接AC、AF、CF。求△AFC的面积。

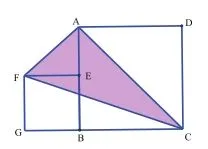
图2

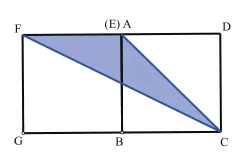
图3

图4

教师和学生共同分析后，利用常规解法（解法略），求出△AFC的面积是8，一切都在教师的预设中。

师：同学们还有什么疑问吗？

生1：老师，我有更简单的方法．因为点E是边AB上任意一点，如果把点E移动到点A处，这两个正方形就是全等的（如图3），△AFC的面积=4×4÷2=8。

师：位置特殊化为我们解决问题提供了一种简明的方法，我们班的同学真是聪明啊！

生2：他能把点E移动到点A处，我也可以把点E移动到点B处（如图4），这样△AFC的面积就是△ABC的面积，即正方形ABCD面积的一半。

生3：老师，这些方法都麻烦，其实△AFC的面积只与正方形ABCD的边长有关，与四边形EFGB的边长没有一点关系！（真是一鸣惊人，全班顿时安静下来，大家都感到很惊奇）

生3：如图5，连接BF，可得BF∥AC,所以△AFC的面积=△ABC的面积=正方形ABCD面积的一半。

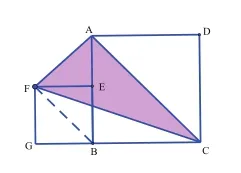
图5

在这个教学过程中，教师在课前也是精心备课，研究了一些解法的，所以当大部分学生的解题思路和课前预设相同时，教师只有按照课前的备课思路朝下进行即可。教师的一句“同学们还有什么疑问吗”给学生的生成提供了展示的机会，学生1的解法确实精彩，教师在教学中追求生成的开放态度，让教师自己和其他学生欣赏了一种新的解法，而教师毫不吝啬的赞美和学生1的精彩解法也刺激了其他学生，当思维被激活以后，前面的生成又促成了学生2的生成。学生1和学生2的解法实质上没有什么区别，但正是学生1的精彩思维激活了其他学生的思维，体现了生成的价值。在这样的教学氛围中，师生在一个个生成中展示自我，欣赏他人。

没有预设，就没有教学，但没有生成的课，也不能说是一堂好课。课堂教学不应当是一个封闭系统，不应拘泥于预先设定的固定不变的程式。传统课堂把“生成”看成一种意外收获，而新课则把“生成”当成一种价值追求，教师应该在精心预设的前提下，努力去追求充满生成的生机勃勃的课堂，并在正确应对生成的过程中实现我们的高效教学，培养和提高学生的数学能力。当然，在课堂上教师要具有一双慧眼，对价值不大的信息和问题要及时排除和处理，使课堂教学回到预设和有效的轨道上来，以保证教学的正确方向；而对那些有价值的生成，教师在教学中要将其视为重要的课程资源，充分加以利用，为自己的教学目标和学生的发展服务。

[1]《全日制义务教育数学课程标准（实验稿）》.北京师范大学出版社，2001（7）.

[2]邹振兴.追求“预设”与“生成”的和谐统一[M].中学数学教学参考，2007.1-2.