让学生在数学实验中自主地获取知识和经验——《“做”菱形之矩形中的菱形问题》课堂教学实录与思考

江苏省苏州工业园区星海实验中学 高 铭

让学生在数学实验中自主地获取知识和经验
——《“做”菱形之矩形中的菱形问题》课堂教学实录与思考

江苏省苏州工业园区星海实验中学 高 铭

一、知识背景

在课堂教学中，尤其是在数学实验的教学中，教师要引导学生自主探究，让学生经历从多角度认识问题、多种形式表达问题、多种策略思考问题的活动，发展其创新意识和应用意识，提高解决问题的能力，感受数学创造的乐趣，增进学好数学的信心，获得对数学较为全面的体验与理解。在此理念指导下，实验教学一定要倡导学生自主学习，强调学生通过观察、实验和探索等切身体验来体会数学探究过程的乐趣，感受数学知识的魅力。

二、师生目标

1.学生达成目标

（1）解决在矩形中做菱形的一般思路和常规方法。

（2）进一步发展学生的推理论证能力。

2.教师达成目标

让学生在实践中自主、愉快学习，创造研究性学习的氛围，引导学生进行深刻的思考，渗透从特殊到一般的数学思想。

三、课前热身

1.题目

如右图，在矩形ABCD中，将△ABD沿着对角线BD翻折，与BC边交于点E，求证：△BED是等腰三角形。

【设计思路】从简单题入手激发学生的兴趣，同时教会学生通过折叠可以产生相等的边或角，再加上平行，可以得到等腰三角形。

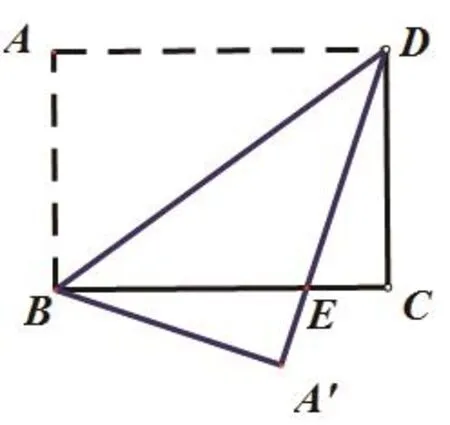
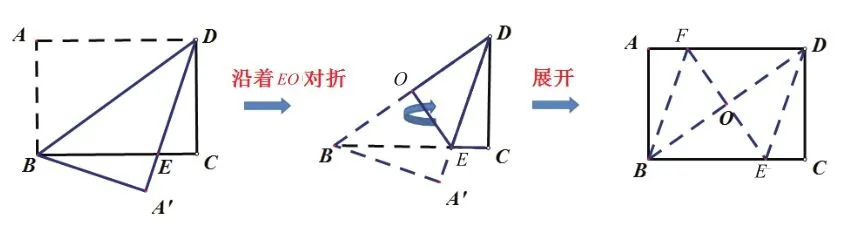
2.追问

按如此折叠的图形展开后，四边形BEDF是一个菱形吗？

【设计思路】引入课题“做菱形”，激发学生去思考，不需要学生马上作答，让学生带着思考进入课堂（板书课题）。此题一方面是为了之后引导学生如何找到矩形的对称中心，从而找到一种折菱形的方式准备，另一方面，也是为后面先折叠产生等腰三角形，进而得到菱形做准备的。

四、课堂操作

（一）课堂操作一：将一张矩形纸片先折叠，再剪一刀，展开，得到一个菱形。

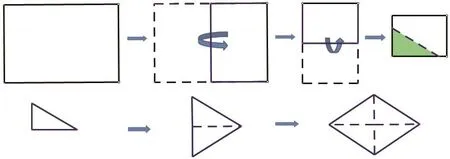
【设计思路】通过较为简单的“剪”的方式，让学生轻松上手。请学生展示成果并说明理由，从而得到对角线互相垂直平分的四边形是菱形，即菱形的一种判定方法。（板书）

（二）课堂操作二：若只通过折叠，你能折出一个菱形吗？

【设计思路】收起剪刀，只通过折叠得到菱形，学生需要思考一定的时间，方法也很多，但是想先通过从一些特殊的方式入手，再回归到一般情况，让学生探索出其中奥妙。

方法1：通过两次对折，找到各边中点，连接各中点折出菱形。

实际课堂交流中，发现不少同学能够找到此方法。

方法2：课前热身的方法。

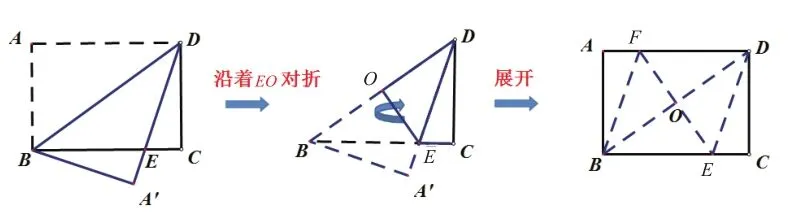
【设计思路】课前热身中已经提出问题，在此让学生先自己折叠，发现原因，给出证明。有前两题做铺垫，学生可以很快证出。本题在此出现的设计意图在于引导学生深刻思考： “为什么这样折叠是菱形？这几种方式有什么共同的特点？”从而带领学生回顾出菱形的一种判定方法：对角线互相垂直的平行四边形是菱形。（板书）

在之前试课时，我发现很少有学生能够发现其共同点：两条对角线都经过矩形的对称中心，所以在正式上课时，笔者给学生做了引导：“前两次的折叠方法中的两次对折之后，两条对角线的交点有什么特点？”这样学生很快就发现了它们的共性。接着又提出问题：“是不是只要两条互相垂直的对角线都经过矩形对称中心，这样构成的四边形就一定是菱形呢？”提出这个问题后，先让学生动手折纸，再请几位同学分别展示成果并作简要证明。在交流过程中，学生一般有以下两种情况：

生1：

生2：

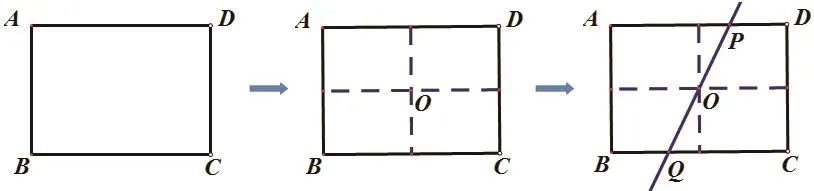
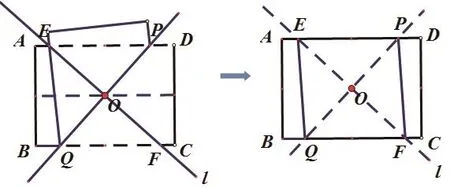
在这里，我们用从特殊到一般的数学思想揭示了本课的第一条主线，即矩形折菱形的第一种一般方法——对角线互相垂直平分。

（三）课堂操作三。

师：之前有位同学发现了一种折菱形的方法，但是他不会证明，请大家帮忙，看看他的折法是否正确？（设置悬念）

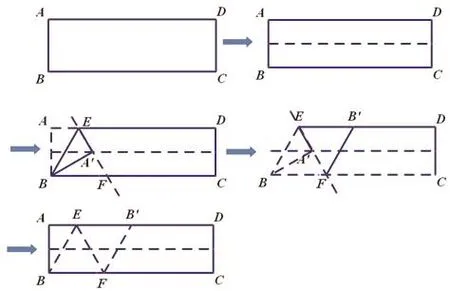
【设计思路】在试课时，我们发现学生按如图方式折叠是没有困难的，但是要他们给出证明，却存在着很大的困难，所以在正式上课时，我们对这个问题进行了重点解析，采用了笔者带着学生一起折叠，一边折，笔者一边提出问题，学生思考并回答。本质意图在于引导学生发现其内在联系，最终做出菱形。

具体过程：

第一步折叠：将矩形对折，展开得到一条折痕。

师：这条折痕对矩形的边AB有何特点？

生：这条折痕是对称轴，进而得到这条折痕是线段AB的垂直平分线。

(3)使用化合物灌浆。化合物灌浆法的原理是堵塞含水层中的孔隙空间，井眼附近含水层中的沙粒与化合物混合后固化并变得密实，此后钻井可以继续进行。可采用的化合物为丙烯酸酯单体配方(AMS)，这种配方适用于温度为50～200 ℃的井下。

师：垂直平分线的性质是什么？

生：垂直平分线上的点到线段两端点的距离相等。

第二步折叠：将矩形的顶点A叠在折痕上，同时所产生的折痕经过点B。

师：这次折叠后，点A落在刚才的垂直平分线上，由垂直平分线的性质我们可以得到什么结论？

生：AA′=BA′。

师：除此之外，可以得到哪些深层次的结论？

（在此要得到一系列的结论，需要一步步慢慢证明，环环相扣，层层递进）

生：△ABA′是等边三角形，∠ABE=∠A′BE=30°，∠AEB=∠A′EB=60°，∠BED=60°。

做好铺垫后，继续追问。

师：EA′所在直线与BC交于点F，你们还有什么发现？

生：△BEF是等边三角形。

第三步折叠：将△BEF沿着EF翻折，再将剩余部分沿边BE折叠，产生折痕，最后展开。

师：将△BEF沿着EF翻折后，点B一定会落在边AD上吗？为什么？

生：由之前得到的结论∠A′EB=60°，∠BED=60°，可知两角相等，所以点B一定会落在边AD上。

师：为什么这些折痕构成的四边形是菱形？

生：由一组对边平行且相等得到平行四边形，再加上一组邻边相等，变成菱形。

（板书：有一组邻边相等的平行四边形是菱形）

师：这个菱形我们可以看作是将等边三角形BEF沿着边EF翻折而成的，那么一般的等腰三角形也沿着它的某条边翻折，也能得到菱形吗？另外，沿着翻折的这条边有什么要求？

【设计思路】学生思考问题的同时，也让学生动手折。先让学生尝试着折等腰三角形，引导学生回到课前热身的问题。课前热身中已经证出△BED是等腰三角形，所以可以从这种熟悉的折法入手。在实际上课中，的确有学生用这种方法。再让学生来证明得出结论：一般的等腰三角形沿着它的底边翻折，也能得到菱形。

师：此种折法中有一个特殊的元素：BD。BD既是菱形的对角线，也是原来矩形的对角线，这很特殊。那么，如果不依托于原来矩形的对角线，你能折出等腰三角形，进而得到菱形吗？

【设计思路】此处将问题再次升级，从特殊到一般，同时也将学生对问题的认识带上一个新境界。

如何不依托于BD就能折出等腰三角形呢？

学生小组讨论后，并没有找到方法，于是笔者带领学生一起折。在折的过程中，学生不仅仅要关注折的“动作”，更重要的是思考折的“道理”，所以在每折一步时，教师都向学生提出问题，引发学生思考。最后学生能够证出菱形并且归纳得到结论：只要将等腰三角形沿着底边翻折，就一定可以折出菱形。

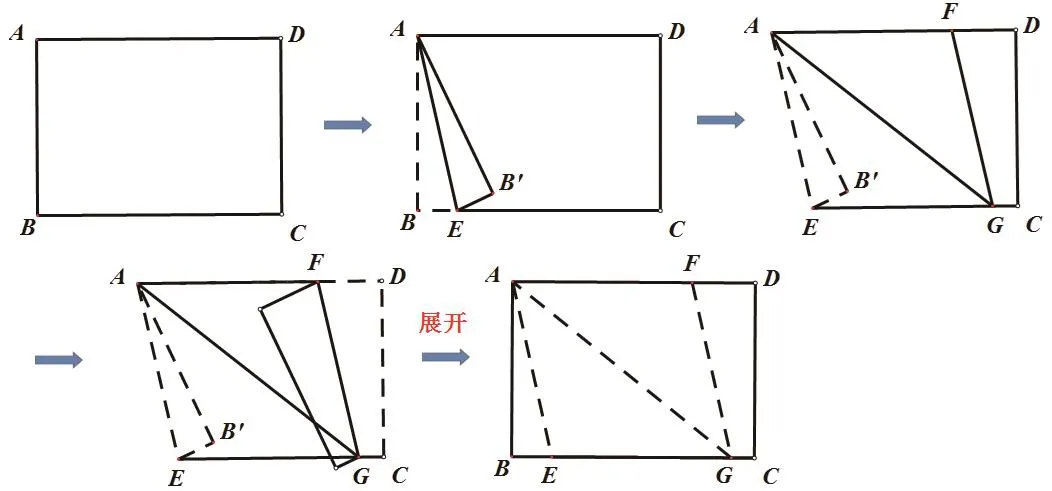
在这里，我们用从特殊到一般的数学思想揭示了本课的第二条主线，即矩形折菱形的另一种一般方法——有一组邻边相等的平行四边形是菱形。

五、课后拓展

请你改造一个矩形，构造一个面积与之相等的菱形。可用工具：剪刀。

【设计思路】这个问题留给学生课后思考，仍然以矩形为载体来构造菱形。学生在已经掌握做菱形的关键之后再来完成此题，学会融会贯通，举一反三。

在课堂实验交流过程中，笔者意外发现了同学折纸作品有许多再创造的现象，我们同时也感受到许多同学有着十分强烈的创造意识。这节课中，课堂交流的气氛异常活跃。

回顾整个实验操作过程，本堂从课前预习题的设计与布置，从儿时的折纸游戏课堂导入开始，逐层递进地向学生提出了矩形中有关折纸的问题。用不同的形式，不同的问题情境呈现了数学问题的研究的不同方向。学生在老师的引导下，用特殊到一般的思想复习巩固数学知识，不断地体验了几何的变化，不断地让学生在变化的过程中体验数学实验的其乐无穷。