基于最弱t-模的飞机起落架模糊故障树分析

刘洪健，姚军，李佩昌

（北京航空航天大学可靠性与系统工程学院，北京100191）

基于最弱t-模的飞机起落架模糊故障树分析

刘洪健，姚军，李佩昌

（北京航空航天大学可靠性与系统工程学院，北京100191）

目的针对飞机起落架部件失效的模糊性以及传统模糊故障树分析中采用扩展原理或区间运算而导致模糊积累的缺点，提出了一种基于最弱t-模的飞机起落架模糊故障树分析新方法。方法采用梯形模糊数表示飞机起落架部件模糊失效概率，给出最弱t-模的模糊运算法则，并利用最弱t-模法则进行模糊故障树分析。结果得到了飞机起落架系统的模糊失效概率以及部件的重要度。结论与传统模糊故障树分析方法比较，该方法具有更加灵活适用的优点，为飞机起落架可靠性评估奠定了基础。

模糊故障树分析；最弱t-模；飞机起落架；模糊数；可靠性评估

飞机起落架作为飞机的重要组成部分，对于飞机的安全起降发挥着至关重要的作用。据研究资料统计，由于起落架结构引起的事故占到飞机结构事故的2/3以上[1]。美国国家运输安全委员会统计，1993—2003年10年内，各类飞机因起落架系统故障引起的飞行不正常事故占不正常飞行事故总数的15%，而其中因起落架收放系统故障引起的事故就占到了23%[2]。飞机起落架的安全性与可靠性受到广泛关注，众多研究者针对飞机起落架的故障分析开展了相关工作，并取得了一定的成果[3—5]。故障树作为广泛使用的系统可靠性分析方法，成功应用于飞机起落架可靠性分析中[6—8]。

在现实中，飞机起落架的故障现象、故障状态以及故障原因等存在大量不确定性。不确定性主要包括随机性和模糊性。基于随机性的不确定性问题通常采用概率论理论进行分析，而模糊性主要是由于信息和认知的缺乏而造成的，包括数据的缺失或不足、故障定义的含糊不清以及环境的改变等[9—10]。为解决模糊性问题，Zadeh[11—12]在1965年开创性提出了模糊集合，采用模糊集定量化描述模糊问题，并于1968年提出了模糊算法。Tanaka等[13]首次将模糊集理论引入故障树分析中，用梯形模糊数来表示基本事件的模糊失效概率，并利用扩展原理计算顶事件的失效概率区间值。在此基础上，众多研究者开展了模糊故障树相关研究，文献[14—17]采用不同模糊运算方法来分析系统模糊可靠性。Huang等[18]基于posbist可靠性理论，提出了一种posbist故障树分析方法，该方法对于历史数据缺失或失效概率很低情形下的可靠性评估具有优势。随着模糊算法的不断发展，模糊故障树分析方法也开始应用于飞机起落架模糊可靠性分析。李瑰贤等[19]采用模糊故障树方法分析了直升机液压系统可靠性，丰世林[20]针对民航运输机刹车系统，采用模糊故障树方法进行了模糊可靠性分析。

以上模糊故障树分析方法都是基于最小边界（sup-min）的评估方法，而这种可靠性评估方法会导致模糊累积。为缓解模糊的积累，Hong and Do[21]采用t-模边界（sup-t-norm）代替最小边界，提出了一种基于最弱t-模的模糊运算法则，并利用L-R型表示部件发生概率。近年来，基于最弱t-模的模糊运算方法受到广泛关注，并成功应用于医疗器械[22]、印刷电路板[23]等众多领域。

基于上述原因，文中采用梯形模糊数表示飞机起落架部件模糊失效概率，给出最弱t-模的模糊运算法则，并利用最弱t-模法则进行模糊故障树分析，从而得到飞机起落架系统的模糊失效概率。与传统模糊故障树分析方法比较，该方法具有更加灵活适用的优点，为飞机起落架可靠性评估奠定了基础。

1 飞机起落架模糊故障树

1.1 最弱t-模模糊运算

实际工程中，许多系统的故障状态、故障现象与故障原因之间存在着大量的不确定性，这种不确定性现象主要表现在随机性和模糊性两方面。对于随机性问题，基于概率统计的方法被广泛采用。对于模糊不确定性，一直以来困扰着广大科研工作者，直到1965年，Zadeh[11]开创性提出模糊集合概念。

最常用的模糊数包括三角模糊数、梯形模糊数和高斯模糊数。早期的模糊运算方法主要是基于扩展原理或区间理论，而这些模糊算法会导致模糊累积现象，进而造成计算结果误差较大。为解决这一问题，t-模被引入到模糊运算中。

t-模是单位区间[0,1]×[0,1]→[0,1]的二元函数T，函数T满足交换律、结合律、单调性和边界条件。

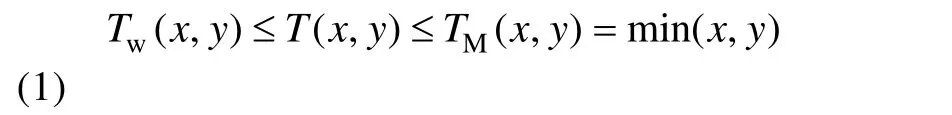
表1 基于Tw的模糊运算

对于两个模糊数，基于TM和Tw的模糊加法和减法运算均可保持原有模糊数的形状。对于模糊乘法运算，基于TM的模糊运算无法保持模糊数原有的形状，而基于Tw的模糊运算则可以保持其形状不变。另一方面，基于Tw的模糊运算方法可以缓解模糊扩展现象，有助于提高计算精度。

1.2 基于最弱t-模的模糊故障树分析(FFTA)

故障树分析作为一种重要的系统可靠性分析方法，主要依赖于基本事件的失效概率及其失效关系。实际工程中，由于数据的缺乏、环境变化等原因，难以获得基本事件的失效概率精确值。为解决这类不确定性问题，采用模糊数来代替精确值的模糊故障树分析被提出。模糊故障树分析的关键在于基本事件间逻辑关系的模糊运算。

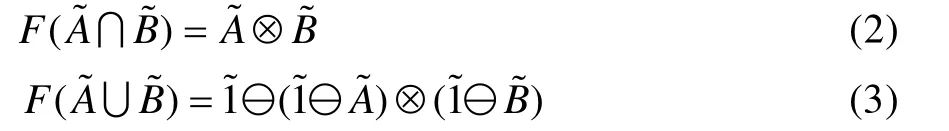
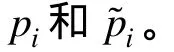
表2 不同方法下的逻辑门输出失效概率

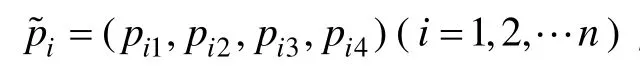
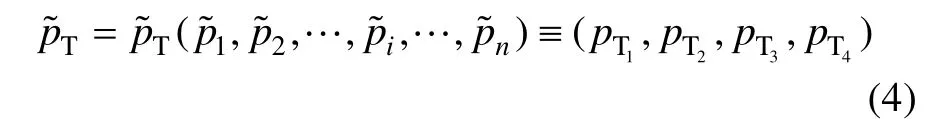
式中：(pT1,pT2,pT3,pT4)为梯形模糊数。

若假定底事件i的失效概率为0，则顶事件的模糊失效概率变为：

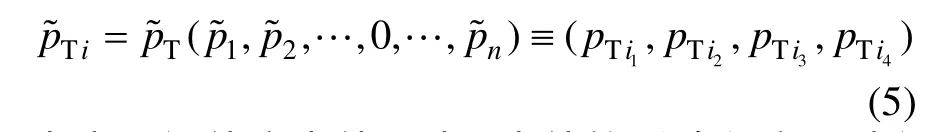
为定量评估底事件i对顶事件的影响程度，引入一种新的重要度定义：

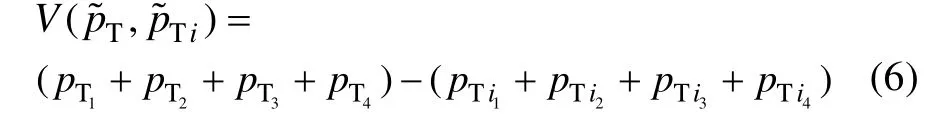
1.3 飞机起落架故障树建立

起落架作为飞机的起降装置，包括缓冲系统、收放系统、机轮刹车系统等，主要用于承受飞机自身重力和着陆时的冲击载荷，吸收并消耗撞击能量和飞机滑跑过程中颠簸产生的能量，保证飞机处于平稳状态。因此，起落架的工作性能对于飞机起飞降落的安全性具有至关重要的作用。由于飞机起降周期较短，起落架的使用相对频繁，而且起落架工作环境恶劣、受力复杂，导致飞机在寿命周期内发生故障的概率高于其他结构。

以某型舰载机为例，对飞机起落架的结构功能进行分析，并收集统计相关故障信息，参考文献[8]，得到飞机起落架的主要失效模式。

对于缓冲系统而言，其主要故障包括减震支柱故障、扭力臂故障、斜撑杆故障以及轮胎故障。其中减震支柱的主要故障包括减震支柱出现渗油、减震支柱断裂、活塞杆和外筒磨损、密封装置受损；扭力臂的主要故障包括轴接头磨损、螺栓磨损甚至断裂；斜撑杆的主要故障包括螺杆的裂纹、衬套的磨损；轮胎的主要故障是轮胎的磨损。

对于收放系统而言，其包括主收放系统（液压收放系统）和备用收放系统（机械收放系统）。液压收放系统的主要故障包括收放锁机构故障、收放作动筒故障以及液压装置故障。其中收放锁机构的主要故障包括连接部位的磨损、锁弹簧的断裂；收放作动筒的主要故障包括收放作动筒渗油、活塞杆变形断裂；液压装置的主要故障包括液压泵故障、液压管路泄漏。机械收放系统的主要故障是应急收放机构故障，包括应急开关无法开启，应急作动筒断裂以及上位锁无法开启等。

对于机轮刹车系统而言，其主要包括机轮故障和刹车组件故障，其中机轮故障主要包括机轮半轴磨损断裂、轴承磨损以及轮胎磨损。

综合以上飞机起落架故障分析，建立了飞机起落架的故障树，如图1所示。

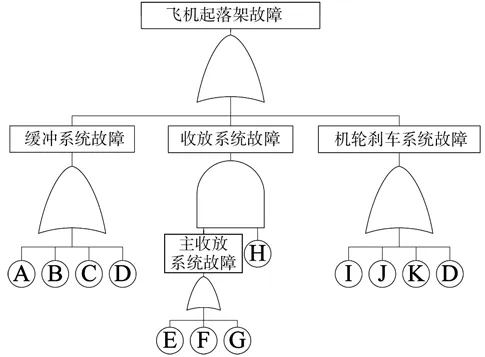
图1 飞机起落架故障树

根据文献[7—8]提供的起落架失效概率或失效率信息，得到了故障树中底事件在100 h工作时间下的失效概率。该失效概率由于飞机样本问题、故障界限不够明确、环境因素变化等问题，导致其数据存在一定的模糊不确定性。因此，根据其近似失效概率，通过梯形模糊数相关准则，仿真得到模糊失效概率，其数据见表3。

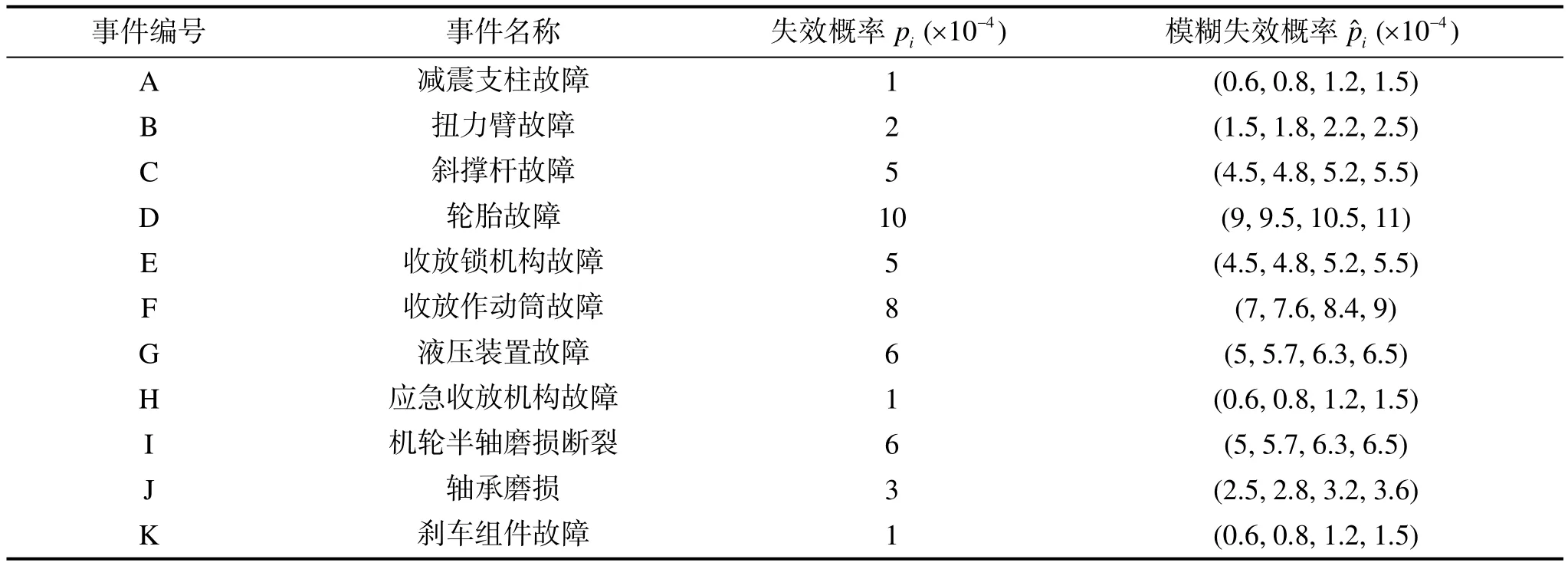
表3 底事件故障概率

2 飞机起落架的模糊可靠性评估

对图1中故障树进行分析，由布尔运算可得顶事件为：

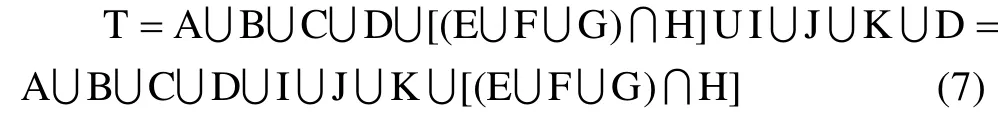
采用不同的可靠性评估方法对飞机起落架的可靠性进行分析评估。

2.1 系统模糊可靠度计算

1）传统故障树分析方法。传统故障树分析依赖于基本事件失效概率精确值以及基本事件间的逻辑关系。由表2和式（7）可知飞机起落架的失效概率为：

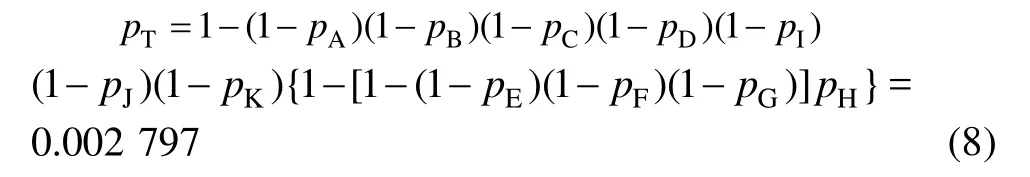
因此，飞机起落架在100 h工作时间下的可靠度为0.99720。

2）Huang方法。当历史数据缺失或失效概率很低时，Huang提出的posbist故障树分析方法对于系统可靠性评估具有较大优势。由于飞机起落架失效概率很低，因此采用该方法对飞机起落架进行可靠性评估。

缓冲系统故障概率：

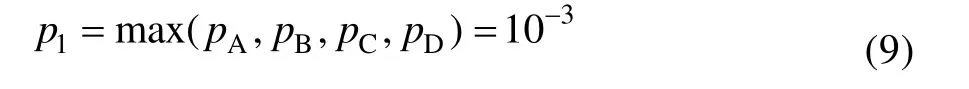
主收放系统故障概率：

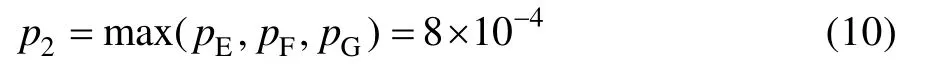
收放系统故障概率：

机轮刹车系统故障概率：

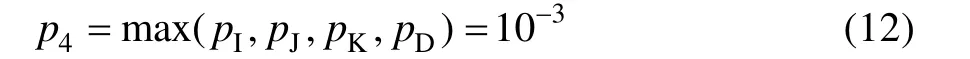
顶事件故障概率：

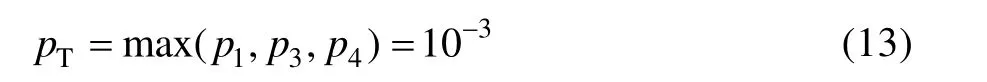
因此，在100 h工作时间下，飞机起落架失效概率为10-3，其可靠度为0.999。

3）Tanaka方法。Tanaka首次将模糊理论引入故障树分析中，利用扩展理论进行模糊逻辑运算，进而得到顶事件的模糊发生概率。综合表2和式（7），可得飞机起落架的模糊失效概率为：

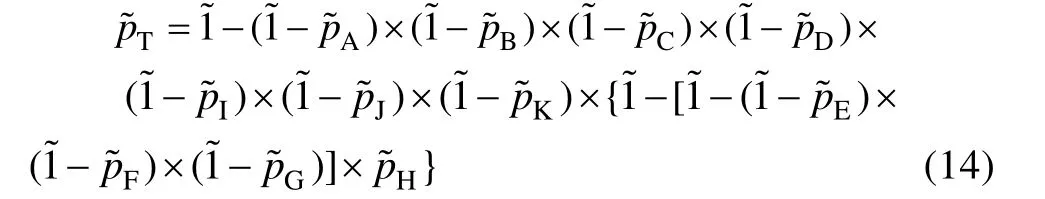
4）文中方法。文中将基于最弱t-模的模糊故障树分析应用于飞机起落架系统，对飞机起落架进行可靠性评估。结合表2最弱t-模运算法则以及式（7），可知飞机起落架的模糊失效概率：

四种方法得到的飞机起落架模糊失效概率的隶属度函数如图2所示。

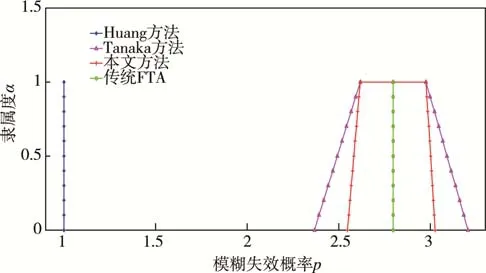
图2 不同方法下的飞机起落架模糊失效概率

由图2可知，文中方法能有效缓解模糊累积现象。考虑到隶属度的置信水平α，不同置信水平下飞机起落架模糊失效概率见表4。

2.2 重要度分析

重要度分析是确定基本事件对顶事件影响显著程度的有效方法。利用式（6）方法得到各基本事件的重要度见表5。

分析表5可知，轮胎和机轮半轴重要度最大，其对飞机起落架可靠性影响最显著。因此，在飞机维修保养中，应重点关注轮胎的损伤以及机轮半轴的疲劳磨损，以保证飞机的安全起降。

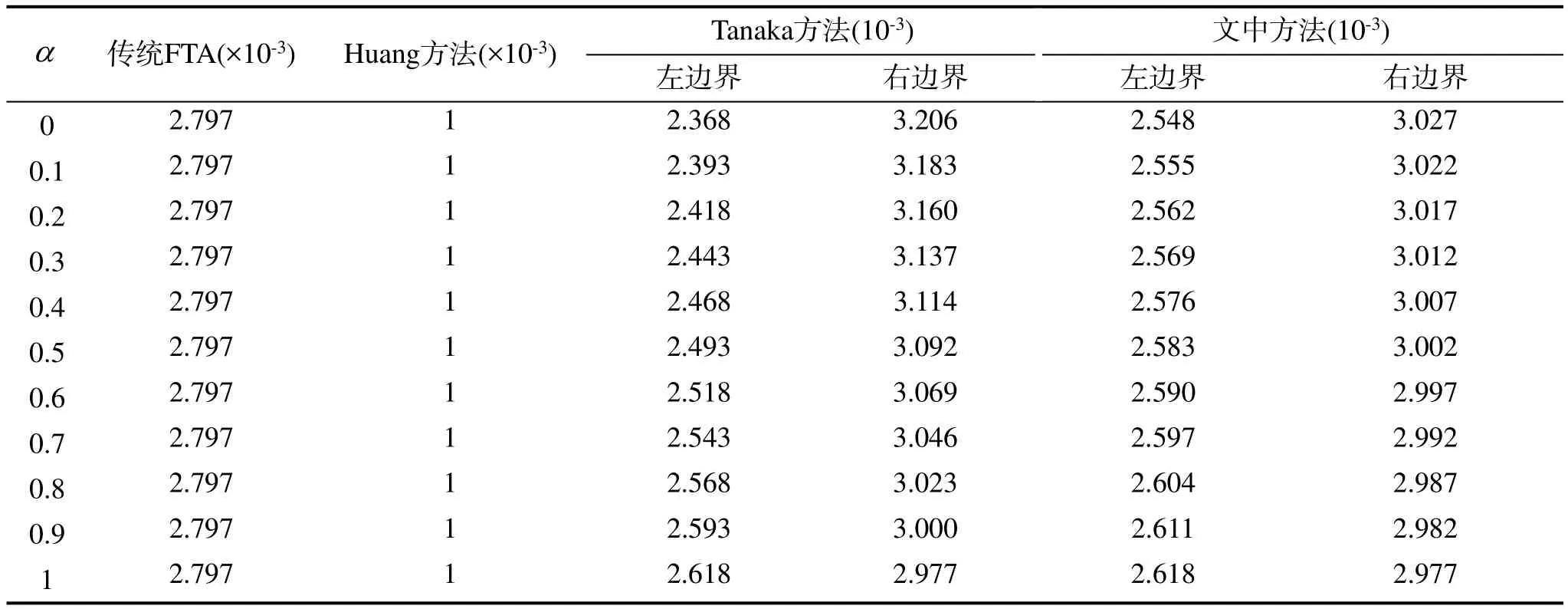
表4 不同方法下飞机起落架α-割集模糊失效概率

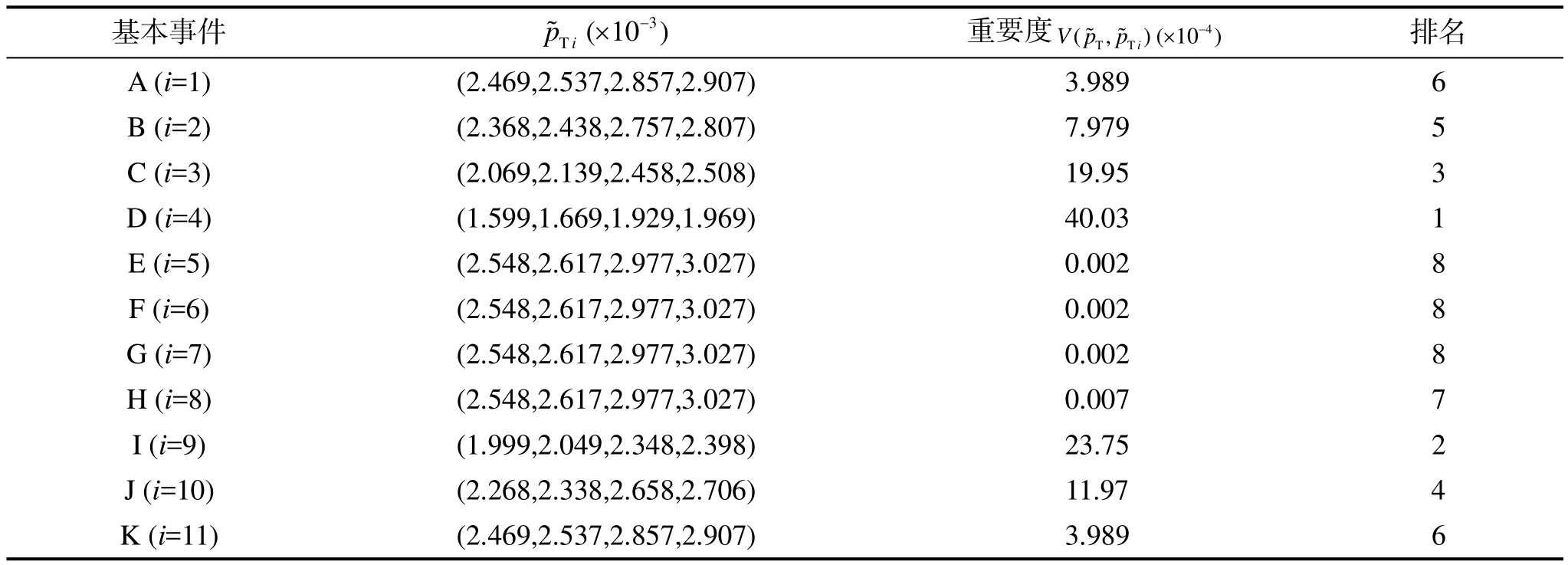
表5 基本事件重要度

3 结论

1）提出了基于最弱t-模的飞机起落架模糊故障树分析方法，解决了飞机起落架故障数据存在不确定性时的可靠性评估问题。

2）与传统模糊故障树分析方法的对比结果显示，文中方法能有效缓解模糊扩展理论和区间运算导致的模糊累积现象，说明了该方法在模糊分析中具有灵活适用的优点。

3）给出了不同置信水平下，飞机起落架系统的失效概率，并确定了飞机起落架部件的重要度，为飞机起落架的部件选用、结构改进以及确定防范措施的顺序提供了依据。

参考文献：

[1]NIE Hong.Fatigue Life Prediction of Aircraft Landing Gear Based on Multi-body System Simulation and Local Strain Method[C]//Fatigue 2000,Proceedings of the Fourth International Conference of the Engineering Integrity Society.Cambridge,England,2000:407—414.

[2]DUPOW H,BLOUNT G.A Review of Reliability Prediction[J].Aircraft Engineering and Aerospace Technology,1997,69(4):356—362.

[3]LEE H C,HWANG Y H,KIM T G.Failure Analysis of Nose Landing Gear Assembly[J].Engineering Failure Analysis,2003,10(10):77—84.

[4]OSSA E A.Failure Analysis of a Civil Aircraft Landing Gear[J].Engineering Failure Analysis,2006,13(7): 1177—1183.

[5]BAGNOLI F,DOLCE F,COLAVITA M,et al.Fatigue Fracture of a Main Landing Gear Swinging Lever in a Civil Aircraft[J].Engineering Failure Analysis,2008, 15(6):755—765.

[6]张峰,徐廷学,赵建忠,等.舰载直升机起落架收放系统事故树的定性分析[J].航空科学技术,2009(5):18—20.

[7]张峰,路坤,徐廷学.事故树的定量分析在某型舰载直升机起落架收放系统中的应用[J].飞机设计,2010, 30(1):64—68.

[8]李佩昌.某型飞机起落架的可靠性分析[D].哈尔滨:哈尔滨工程大学,2010.

[9]ZIO E.Reliability Engineering:Old Problems and New Challenges[J].Reliability Engineering and System Safety, 2009,94(2):125—141.

[10]SURESH P V,BABAR A K,RAJ V V.Uncertainty in Fault Tree Analysis:A Fuzzy Approach[J].Fuzzy Sets and Systems,1996,83(2):135—141.

[11]ZADEH L A.Fuzzy Sets[J].Information and Control, 1965,8(65):338—353.

[12]ZADEH L A.Probability Measures of Fuzzy Events[J]. Journal of Mathematical Analysis and Applications,1968, 23(2):421—427.

[13]TANAKA H,FAN L T,LAI F S,et al.Fault-Tree Analysis by Fuzzy Probability[J].IEEE Transactions on Reliability,1983,R-32(5):453—457.

[14]SINGER D.A Fuzzy Set Approach to Fault Tree and Reliability Analysis[J].Fuzzy Sets and System,1990, 34(2):145—155.

[15]MON D L,CHENG C H.Fuzzy System Reliability Analysis for Components with Different Membership Functions[J].Fuzzy Sets and Systems,1994,64(2): 145—157.

[16]CHEN S M.Fuzzy System Reliability Analysis Using Fuzzy Number Arithmetic Operations[J].Fuzzy Sets and Systems,1994,64(1):31—38.

[17]MON D L,CHENG C H.Fuzzy System Reliability Analysis for Components with Different Membership Functions[J].Fuzzy Sets and Systems,1994,64(2): 145—157.

[18]HUANG H Z,TONG X,ZUO M J.Posbist Fault Tree Analysis of Coherent Systems[J].Reliability Engineering and System Safety,2004,84(2):141—148.

[19]李瑰贤,于广滨,马良.基于模糊故障树直升机起落架液压系统的故障诊断方法研究[J].机床与液压,2007, 35(5):214—216.

[20]丰世林.基于模糊故障树的民航运输机着陆防滞刹车系统故障诊断研究[J].液压与气动,2010(5):77—80.

[21]HONG D H,DO H Y.Fuzzy System Reliability by the Use of Tw the Weakest t-norm on Fuzzy Number Arithmetic Operations[J].Fuzzy Sets and Systems,1997, 90(3):307—316.

[22]KOMAL.Fuzzy Fault Tree Analysis for Patient Safety Risk Modeling in Healthcare under Uncertainty[J]. Applied Soft Computing,2015,37:942—951.

[23]KUMAR M.Applying Weakest t-norm Based Approximate Intuitionistic Fuzzy Arithmetic Operations on Different Types of Intuitionistic Fuzzy Numbers to Evaluate Reliability of PCBA Fault[J].Applied Soft Computing,2014,23(5):387—406.

[24]HONG D H.Fuzzy Measures for a Correlation Coefficient of Fuzzy Numbers under Tw(the Weakest tnorm)-based Fuzzy Arithmetic Operations[J].Information Sciences,2006,176(2):150—160.

Fuzzy Fault Tree Analysis of Aircraft Landing Gear Based on Weakest T-norm

L IU Hong-jian,YAO Jun,L I Pei-chang
(School of Reliability and System Engineering,Beihang University,Beijing 100191,China)

ObjectiveAccording to disadvantages of fuzziness on failure of landing gear components and application of extension principle and interval arithmetic in traditional fuzzy fault tree analysis leading to accumulation of fuzziness,this paper aims to propose a new analysis method for fuzzy fault of aircraft landing gear based on the weakest t-norm.MethodsThe fuzzy failure probability of aircraft landing gear components was represented by trapezoidal fuzzy number, and the fuzzy operation rules of the weakest t-mode were given,and the fuzzy fault tree analysis was carried out with the weakest T-norm rule.ResultsThe fuzzy failure probability of aircraft landing gear system and the importance of components were obtained.ConclusionCompared with the traditional fuzzy fault tree analysis method,the proposed method is more flexible and applicable,which lays a foundation for the reliability assessment of aircraft landing gear.

fuzzy fault tree analysis;weakest t-norm;aircraft landing gear;fuzzy number;reliability assessment

10.7643/issn.1672-9242.2017.07.021

TJ85；TG405

A

1672-9242(2017)07-0103-06

2017-03-18；

2017-04-06

刘洪健（1990—），男，河北人，硕士,主要研究方向为可靠性与环境试验技术。

姚军（1976—），男，北京人，高级工程师，主要研究方向为可靠性与环境试验技术。