习题设计与思维培养

刘建宁 / 本溪市化学工业学校

习题设计与思维培养

刘建宁 / 本溪市化学工业学校

本文通过对习题的精心设计，从四个方面来阐述如何培养学生的思维能力，启迪学生的智慧。

变式设问；深刻性；一题多解；广阔性；变换习题；创新性；多变习题；变通性

培养学生的思维能力是数学教学的目的之一，在数学教学中思维能力的培养有赖于对数学问题的解决，而数学问题一般表现为习题形式，所以习题教学是培养学生思维能力的重要途径。在习题教学中，习题设计是数学教师的经常性工作，习题设计技巧的高低不仅直接影响着学生的积极性，而且关系到学生创造性思维的训练和培养。因此应重视习题设计技巧即重视编拟设计一些训练学生创造思维品质的习题，以促进学生多想、多疑、启迪学生的智慧。本文就通过习题设计有效 地培养学生思维谈一些具体做法，供参考。

一、变式设问，培养思维的深刻性。

案例一：如图1线段AB（｜AB｜=2a）的两个端点A、B分别在x轴、y轴正半轴上滑动，求△AOB的最小面积。

变式1：如图1直线过点p（2,1）分别交x轴、y轴正半轴A、B两点。探讨①求△AOB的面积何时最小？②△AOB的周长何时最小？③线段AB的长何时最短？

变式2：如图2线段AB（｜AB｜=2a）的两个端点A、B分别在两射线了L1：2x-y=0（x≥0），L2：2x=y=0（x≥0）上滑动，求△AOB的最小面积。

变式3：如图3直线过点p（2,1）分别交两射线L1：2x-y=0（x≥0），L2：2x=y=0（x≥0）A、B，求△AOB的最小面积。

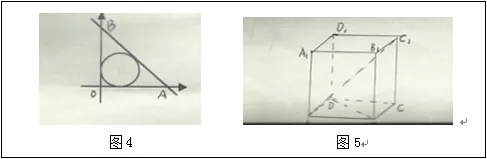
变式4：如图4已知与圆C：（x-r）2+(y-r)2=r2相切的直线交x轴、y轴正半轴A、B两点，O为原点。当切线L绕圆C转到时你觉得那些问题值得我们去探索？（提出开放性问题）探讨①△AOB的面积有无最值？是最大值还是最小值？②△AOB的周长有无最值？是最大值还是最小值？③线段AB的长有无最值？是最大值还是最小值？④｜OA｜+｜OB｜有无最值？是最大值还是最小值？⑤AB中点的轨迹。设问：中点的轨迹是什么？渐近线方程是什么？过中点作渐近线的平行线所围成平行四边形是常数吗？

变式5：（扩展）如果我们把圆扩展到椭圆或双曲线，上述哪些性质还可以延续？哪些性质有所变化？

二、一题多解，灵活运用，培养思维的广阔性。

案例二：如图5在正方体中，求证：AC1⊥BD。设问：1.A C1与BA1的关系如何？2.AC1与DA1的关系如何？3. AC1与面BDA1的关系如何？4.AC1还与哪个面垂直？5. 四面体C1-ABC中有多少个直角三角形？

三、变换习题，培养思维的创新性。

学生思维的创新性主要表现在学习数学过程中善于独立思考和分析问题，善于发现矛盾，提出问题，有探索和猜想的创新精神。

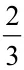
四、多变习题，培养思维的变通性。

设计多变型习题是指教师在习题教学中不要就题论题，要在原题的基础上不断变换问题情境，使之变为更多的有价值、有新意的新问题。使更多的知识得到应用，从而获得“一题多练”“一题多得”的效果，使学生思维的变通性得到培养和发展。

案例四：求曲线y2=-4-2x上与原点距离最近的点的坐标。答案（-2,1）抛物线的顶点。

变式1：求曲线y2=4-2x上与原点距离最近的点的坐标。答案（1，±）此点不是抛物线的顶点，抛物线对称轴上的点到抛物线最近距离不一定在抛物线的顶点处。学生可能会用图像法直接观察出该点在顶点处。此题设计目的是通过辨析，揭示问题的实质，培养思维的准确性。

变式2：求曲线y =-4-2x上与A（a,0）距离最近的点的坐标。答案a≥-3时（-2,0），a＜-3时（a+1，±）本题实际上是前两题的归纳和总结。

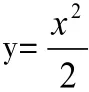
在数学习题教学中如何进行创造教育是一个较大的理论课题，又是我们每个数学教师所面临的最紧迫的实际问题。需要我们去领会和研究，本文只是对该课题的研究作出一个初步的尝试，所提出的也只是很小一部分，还有待于深入地进行理论研究和探讨。

最后，用美国数学家波利亚的话作为结束语：“一个专心备课的教师能拿一个有意义的但不太复杂的题去帮助学生发掘问题的各个方面，使得通过这道题就好象通过一道门户，把学生引入一个完整的理论领域。”

[1]《数学》（全日制普通高级中学教科书）.人民教育出版社中学数学室编著.

刘建宁（1967.12—）女，辽宁本溪人，从事数学教学工作，讲师。