基于Kalman固定点平滑的综合校正陀螺漂移误差评估方法

徐英蛟

（91851部队葫芦岛125000）

基于Kalman固定点平滑的综合校正陀螺漂移误差评估方法

徐英蛟

（91851部队葫芦岛125000）

由于长航时惯导系统进行综合校正后陀螺漂移的补偿效果缺乏直接评估的方法，论文提出一种利用Kalman固定点平滑的校正后陀螺漂移误差定量评估方法。结合综校后惯导系统的输出信息，通过引入高精度的差分GPS和天文导航信息，以速度、位置、姿态构造复合观测量进行匹配滤波平滑，实现校正后残留陀螺常值漂移的精确定量估计。仿真结果表明，该方法可以在40min内有效地估计出综合校正结束时刻的陀螺漂移误差，估计误差在10%之内，且在姿态重调精度较高时，估计的速度与精度均有所提升。

惯导系统；综合校正；陀螺漂移；Kalman固定点平滑

Class NumberU666.1

1 引言

为了抑制惯导误差发散，惯导系统必须依靠外界信息进行定期的综合校正，重调导航误差参数，并对惯性器件误差进行估计和补偿［1］。部分学者利用间断获取的外部参考位置、速度信息进行综合校正，计算等效陀螺漂移并进行补偿［2］。部分学者研究了综合校正中误差补偿所引起的超调抑制方法，实现了综合校正过程的平滑过渡［3］。就各种校正方法的性能而言，现有研究都是对导航参数误差进行间接表征［4～5］，并没有直接评估校正性能的方法，特别是缺乏对校正结束时刻校正效果的定量分析方法。因此开展对校正完成时刻的陀螺漂移余留误差评估方法有着重要的实际意义。

本文采用最优估计中的平滑算法，引入差分GPS系统（DGPS）的速度、位置以及天文导航系统（CNS）提供的姿态信息，与惯导信息进行“速度+位置+姿态”匹配滤波，并利用Kalman固定点平滑算法估计出校正完成时刻的陀螺漂移。方程为

2 惯导系统的误差模型

选用地理坐标系作为惯导的导航坐标系n系，舰船载体坐标系记为b系，地心惯性坐标系记为i系，下面给出动基座下惯导系统误差方程。

2.1 姿态误差方程

结合式（1）、式（2），通过忽略二阶小项，可得到惯导的姿态误差方程为

2.2 速度误差方程

已知捷联式惯导系统的速度基本方程为

则惯导系统速度误差δV的微分方程为

2.3 位置误差方程

位置误差的微分方程为

式中，φ为纬度，λ为经度，分别用δφ、δλ表示纬度、经度误差；RM为子午圈曲率半径，RN为卯酉圈曲率半径。

考虑与滤波过程中外部位置信息观测量统一，采用位置误差的非经纬度描述微分方程，即需要将经纬度转换为东向、北向位置误差δPx、δPy，转换

3 Kalman固定点平滑算法

依据惯导参数一段时间内的观测值，可用Kalman平滑的方法估计出初始时刻的惯导系统误差，这也是对惯导误差进行精度评估的主要思想［6］。R-T-S固定区间平滑算法，需存储滤波过程产生的4个矩阵数据，在滤波结束后再进行平滑［7～8］。然而，高维的数学模型以及较快的解算频率使得需快速存储大量的数据，将有可能造成数据实时性的问题，因此本文采用可以实时递推解算的固定点平滑算法。

设离散系统的状态空间描述为

式中，Xk为系统状态变量，Φk，k-1为系统一步转移矩阵，Wk-1为系统噪声，Zk为量测量，Hk为量测矩阵，Vk为量测噪声。

基于Kalman滤波方程，利用扩充状态变量的方法，将扩充与滤波状态变量一一对应的平滑状态量，可推得固定点平滑方程［9］。Kalman固定点平滑算法的解算步骤为

1）完成滤波值与平滑值的初始化：

式中，m表示状态变量的维数。

2）依据状态方程进行一步预估计，并计算一步预估计协方差阵：

3）计算滤波增益矩阵，并结合量测量修正一步预估计值，得到滤波值：

4）计算平滑增益矩阵，并结合量测量修正上一步平滑值，得到固定点平滑值：

5）计算滤波协方差阵与平滑协方差阵：

4 滤波器设计

4.1 状态变量

设置待估计的13维状态变量X为

4.2 状态方程

考虑对校正后陀螺漂移量的高精度平滑，选用较为精确的惯导数学模型描述，其状态方程为［10，11］

4.3 量测方程

作为评估用的惯导外部参考基准源，其精度必须比相应的惯导信息高一个或几个数量级。本文选择能够提供精确位置、速度信息的DGPS，及能提供精度达到10″量级姿态信息的CNS，构建组合观测基准［12］。量测方程可表示为

5 仿真条件设置

5.1 仿真时间设置

仿真时长为2400s，仿真步长为0.1s。

5.2 误差参数设置

陀螺常值漂移为0.004°/h，陀螺随机噪声为0.001°/h；加速度计零偏为10-4g，加速度计随机噪声为0.5×10-4g；初始速度误差0.01m s，初始北向位置误差为5m、初始东向位置误差为8m； DGPS系统速度量测噪声为0.01m s，天文导航系统姿态量测噪声10″。

5.3 载体运动设置

初始纬度45.7796°，初始经度126.6705°。运动方式：沿北偏东45°航向作匀速直线运动，速度为4节。摇摆方式：

纵摇：周期3s，幅值3°，初值0°；横摇：周期5s，幅值5°，初值0°；航向：周期7s，幅值2°，初值45°。

5.4 滤波器初始值设置

6 仿真结果及分析

以上述仿真条件，分别在初始姿态误差为0°、2″及10″时，分别进行10组仿真后平均结果如表1～表3所示。

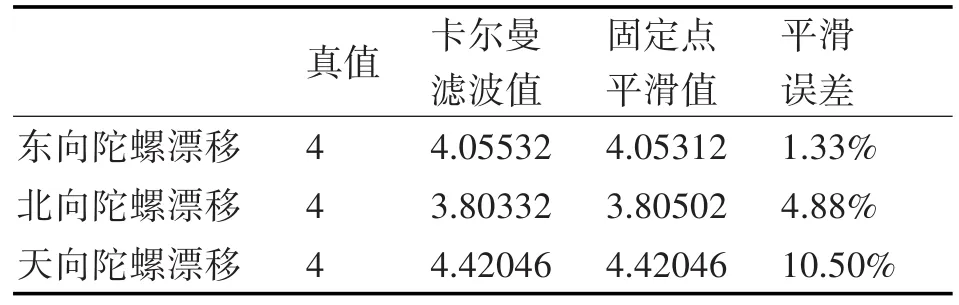
表1 初始姿态误差0°为时的仿真结果（单位：10-3°/h）

陀螺漂移的固定点平滑仿真结果如图1所示。

图1陀螺漂移的固定点平滑仿真曲线

陀螺漂移的固定点平滑仿真结果如图2所示。陀螺漂移的固定点平滑仿真结果如图3所示。

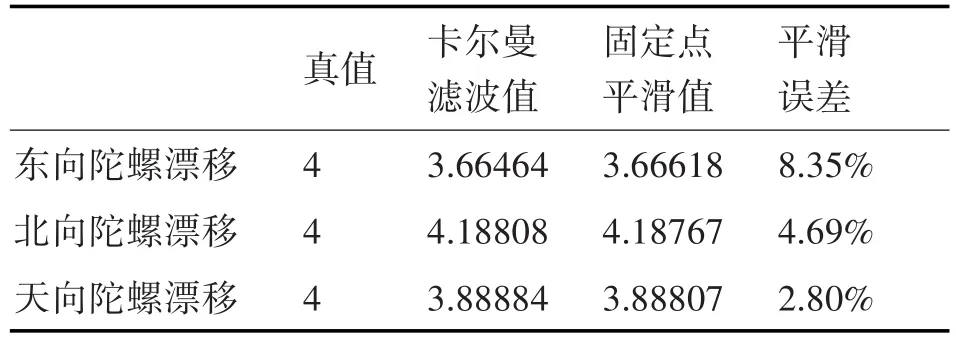
表2 初始姿态误差为1″时的仿真结果（单位：10-3°/h）

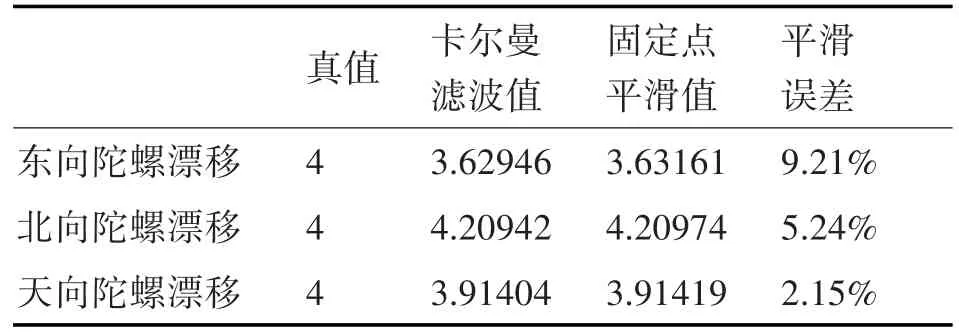
表3 初始姿态误差为10″时的仿真结果（单位：10-3°/h）

由表1～表3可知，经过约40min的匹配滤波可以精确平滑出校正结束时刻的陀螺漂移，平滑误差均在10%之内，只有表1中天向陀螺漂移的平滑精度在10%左右。而陀螺漂移的平滑精度受平滑开始时刻的系统初始姿态误差影响较大，对比图2、图3可知其特征表现为：当初始姿态误差较大时，东向、北向陀螺漂移的平滑精度下降，收敛速度变慢，图3在30min时已基本收敛，而图2约需40min；而天向的陀螺漂移则与之相反，在初始姿态误差较大时，可获得较好的平滑精度，这主要是由于天向陀螺漂移所激励的导航信息误差受初始姿态误差的影响，更大程度地在惯导误差中得到了体现。然而，过大的初始姿态误差也将使导航信息过快的发散，成为产生导航参数误差的主要误差源，且表现为明显的振荡，此时若进行长时间的匹配滤波平滑没有多大的实际意义。因此，为了在有效观测时间段内有效地平滑出惯导系统的陀螺漂移，应在综合校正环节尽可能的实现高精度的姿态重调。

图中固定点平滑曲线与滤波估计曲线几乎重合，这主要是由于较小的陀螺漂移使一步预测误差协方差阵Pk，k-1趋近于奇异阵，导致固定点平滑增益矩阵与滤波增益矩阵Kk几乎相等，从而使两者的曲线趋于重合。

7 结语

本文针对舰船惯导综合校正性能的定量评估问题，提出了一种利用Kalman固定点平滑算法的陀螺漂移精度评估方法。仿真结果表明：该方法可实现对综合校正后的惯导系统陀螺漂移的精确平滑，结合综校中的陀螺漂移补偿量，可以定量地评估综合校正的性能，并重点分析了综校重调后初始姿态误差对陀螺漂移平滑精度的影响，指出提高姿态重调精度是提升陀螺漂移平滑性能的有效措施。

［1］高钟毓.惯性导航系统技术［M］.北京：清华大学出版社，2012：401.

［2］冯培德，李魁，王玮等.一种新的舰载惯导系统综合校正方法［J］.中国惯性技术学报，2011，19（2）：427-435.

［3］程建华，郝燕玲，孙枫等.自动补偿技术在平台式惯导系统综合校正中的应用研究［J］.哈尔滨工程大学学报，2008，29（2）：40-44.

［4］Grewal M S.Application of Kalman filtering to the calibration and alignment of inertial navigation systems［J］. IEEE Trans.Automat Control（S0191-2216），1991，6（11）：3325-3334.

［5］Z F Syed，P Aggarwal，C Goodall，et al.A new multi-position calibration method for MEMS inertial navigation systems［J］.Meas.Sci.Technol，2007（18）：1897-1907.

［6］Kain J.E，Cloutier J.R．Rapid Transfer Alignment for Tactical Weapon Applications［C］//Proceedings of the AIAA Guidance Navigation and Control Conference，Boston，1989：1290-1300.

［7］Watanabe K．A new forward-pass fixed-interval smoother using the UD information matrix factorization［J］.Auto-matica，1986，22（4）：465-475.

［8］宫晓琳，张蓉等.固定区间平滑算法及其在组合导航系统中的应用［J］.中国惯性技术学报，2012，20（6）：687-693.

［9］刘建业，袁信.GPS/INS组合导航系统的平滑滤波应用研究［J］.航天控制，1995（4）：36-42.

［10］徐景硕，秦永元，顾冬晴.惯导系统动基座对准精度评估方法［J］.火力与指挥控制，2005，30（4）：20-23.

［11］杨艳娟，金志华，田蔚风，等.R-T-S平滑算法在捷联惯性导航系统初始对准精度事后评估中的应用［J］.上海交通大学学报，2004，38（10）：1744-1747.

［12］Titterton D H，Wseton J L.Strapdown Inertial Navigation Technology［M］.Second Edition.United Kingdom：Institution of Electrical Engineerings，2004：387-393.

Evaluation Method of Integrated Calibration Gyroscope Drift Error Based on Kalman Fixed Point Smoothing

XU Yingjiao
（No.91851 Troops of PLA，Huludao125000）

In order to directly evaluate the compensation effect of gyroscope drift in the comprehension calibration of long-term shipborne inertial navigation system（INS），a quantitative evaluation method based on Kalman fixed-point smooth algorithm is presented.In this paper，with the output of INS after calibration，high precision information of differential GPS and celestial navigation system are introduced.Accordingly，the velocity，location and attitude errors of INS are involved as the muti-observations which are used in matched filtering and smoothing，achieving the accurately quantitative evaluation of gyroscope drift which is residual after calibration.The simulation result shows that by this method residual gyroscope drift after calibration can be estimated within 40 minutes and the estimation error is less than 10%.Moreover，if the attitude could have been well re-adjusted，the performance of evaluation method will be advanced both in the estimated rapidity and precision.

INS，comprehensive calibration，gyroscope drift，Kalman fixed-point smooth

U666.1

10.3969/j.issn.1672-9730.2017.07.024

2017年1月17日，

2017年2月20日

徐英蛟，男，硕士研究生，助理工程师，研究方向：组合导航。