基于有限元—统计能量数值混响室法的声学包设计与优化
2017-08-05杨德庆石嘉欣郁扬
杨德庆,石嘉欣,郁扬
1高新船舶与深海开发装备协同创新中心,上海200240 2上海交通大学海洋工程国家重点实验室,上海200240 3上海交通大学船舶海洋与建筑工程学院,上海200240
基于有限元—统计能量数值混响室法的声学包设计与优化
杨德庆1,2,3,石嘉欣1,2,3,郁扬1,2,3
1高新船舶与深海开发装备协同创新中心,上海200240 2上海交通大学海洋工程国家重点实验室,上海200240 3上海交通大学船舶海洋与建筑工程学院,上海200240
[目的]为解决传统声学包设计法耗时、耗资高的问题,[方法]利用有限元—统计能量(FE-SEA)数值混响室法在全频段进行声学包的设计与优化。设计空气层声学包及无空气层声学包这2种类型共8种声学包,计算其隔声量。采用遗传算法,以达到最大隔声量值为目标对每一种声学包的材料层厚度进行优化。[结果]研究表明,有空气层存在的声学包的隔声量值较无空气层声学包的高2~6 dB,且与原始设计相比,优化后的声学包的隔声性能得到大幅提高。[结论]所得研究成果对实际工程中船舶声学包设计有重要的指导价值。
声学包;优化;FS-SEA数值混响室法;隔声量
0 引 言
随着新能源及绿色船舶设计技术的发展,噪声作为影响舒适性的重要因素,越来越受到人们的重视。国际海事组织和各国船级社也陆续出台了严格的船舶噪声规范,降噪成为船舶行业的技术热点。声学包作为解决降噪问题的新技术和新产品,受到广泛关注。所谓声学包,是指将阻尼材料、吸声材料、隔声材料以及防火材料等通过装饰面板、衬板或封装面板,制作成一定形状的层合结构,以实现降低指定频段范围内一定量级噪声及振动的声学处理元件。汽车行业是较早开始采用声学包技术来提升汽车声学环境舒适性的一个领域[1-4]。本文拟利用数值模拟手段研究声学包的设计和优化方法,探索声学包在船舶领域的应用。数值模拟是声学包设计的重要手段,可规避实验测试的成本高、周期长等问题,在理论研究及产品开发阶段更能缩短设计周期,适于产品多样性设计。范明伟[5]和高处[6]利用统计能量(SEA)数值混响室法进行了声学包设计,这种方法的缺点在于单板及两侧声腔子系统在低频段(100 Hz以下)不满足SEA法对子系统单位带宽模态数大于5的要求,其计算结果在低频段不精确、不可信。在声学包的优化方面,苏朝勇[7]利用SEA数值混响室法对声学包进行了优化设计,但在低频段仍然存在计算结果不可信的问题。常规声学包主要用于中、高频的降噪,但在降噪设计中声学包的低频性能也是需要考虑的,不能总是忽略不计。在有些情况下,需要在声学包内加入阻尼材料来进行低频减振降噪设计,这时就需进行低频段计算,所以未来的声学包设计不应仅针对中、高频,还需覆盖全频段。
本文将采用适用于全频段的有限元—统计能量(FE-SEA)数值混响室法进行声学包的设计[8],将其作为评价声学包性能的参数,得到声学包的隔声量。FE-SEA数值混响室法可以很好地解决低频域声学包材料单位带宽模态数不够的问题,从而得到较精确的声学包全频段的隔声量。此外,还将利用遗传算法对含空气层与不含空气层这2种类型的声学包进行优化设计,提升声学包的性能,达到更佳的降噪效果。同时,分别探讨在约束声学包整体厚度情况下声学包的优化效果。所得结果用于为实际工程设计提供参考。
1 声学性能数值分析理论与方法
声学包的声学性能是指在某一频段声学包可以实现的降噪指标或振动衰减量,如隔声量或插入损失。声学包声学性能评定的常规手段是声学实验测试,如混响室法和驻波管法。本文采用FE-SEA数值混响室法代替声学实验测试,具体原理如下。
1.1 FE-SEA耦合声学分析原理
FE-SEA耦合分析方法将声场分为直接场和混响场,前者定义为由入射波产生的声场,后者指经过一次以上反射形成的声场。结构响应q可以写为以下形式[9-10]:
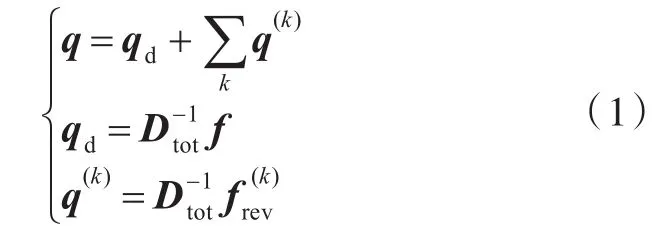
子系统j输入到直接场的平均功率为:

以上式中:ω为圆频率;Pin,j为子系统j输入到直接场的平均功率;为外载荷输入到子系统j的功率;Pout,j为子系统j输出到混响场的平均功率;Sqq为响应q的互谱矩阵,系统有限元模型的动力刚度矩阵;Sff为外载荷的互谱矩阵;D(k)dir为有限元与统计能量模型连接处的动力刚度矩阵;Dd,rs为系统有限元模型的动力刚度矩阵;Ek,nk分别为子系统k的振动能量和模态密度;ηj为子系统j的损耗因子;ηjk为统计能量模型的耦合损耗因子;ηd,j为有限元模型计算的损耗因子;下标rs为随机子系统j确定性边界上的自由度。其中式(7)和式(8)是FE-SEA混合分析理论的主要方程。
1.2 FE-SEA数值混响室法
FE-SEA数值混响室法[8]简称为FS数值混响室法,是通过建立构件的有限元模型,在构件的一侧建立半无限流场(SIF)并与构件联接来模拟声学及结构特性。在构件另一侧,施加混响激励以模拟实际声学边界条件,并在有限元构件处施加简支边界条件。试件尺寸可根据实际结构设置,若无具体要求,在评价某材料声学性能时建议选取测试件大小为350 mm×220 mm的长方形结构,半无限流场与待测试件之间的距离建议取为500mm。作为入射声源的混响声源的声压值,应在各测试频率下均相同且稳定,建议取为1 Pa(等效于94 dB)。求解该FE-SEA耦合模型,通过入射声源激励和半无限流场处的声压值,可以得到待测试件的隔声量。上述算法实现及模型建立是采用VA One 2013软件完成的,原理如图1所示。
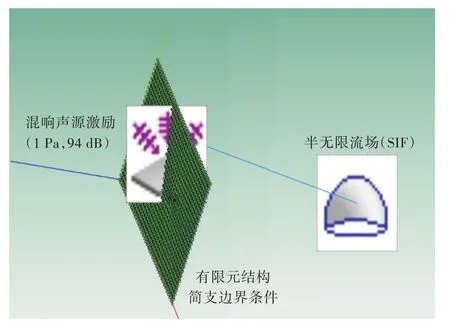
图1 FS数值混响室法示意图Fig.1 Schematic of FS numerical reverberation method
2 声学包隔声量的FE-SEA数值混响室法计算
2.1 FE-SEA耦合声学分析算例
建立如图1所示的FS数值混响室法模型,构件为铝板,尺寸为350 mm×220 mm×1 mm,弹性模量为71.0 GPa,泊松比为0.33,密度为2.81×103kg/m3,阻尼损耗系数为0.1%。半无限流场距铝板500 mm,混响声源强度的取值为1 Pa(等效于94 dB)。结构约束边界条件为简支,计算频率16~125 Hz。低频段(125 Hz以下)FS数值混响室法与瑞利李兹理论解法的隔声量结果[8]如图2所示。
计算结果表明,125 Hz以下FS数值混响室法得到的铝板的隔声量与瑞利李兹理论计算方法所得结果吻合较好。而有关125 Hz以上该模型的准确性,文献[11]已进行了验证,证明其隔声量计算结果与实验结果吻合较好,FS数值混响室法可用于全频段隔声量的精确计算。
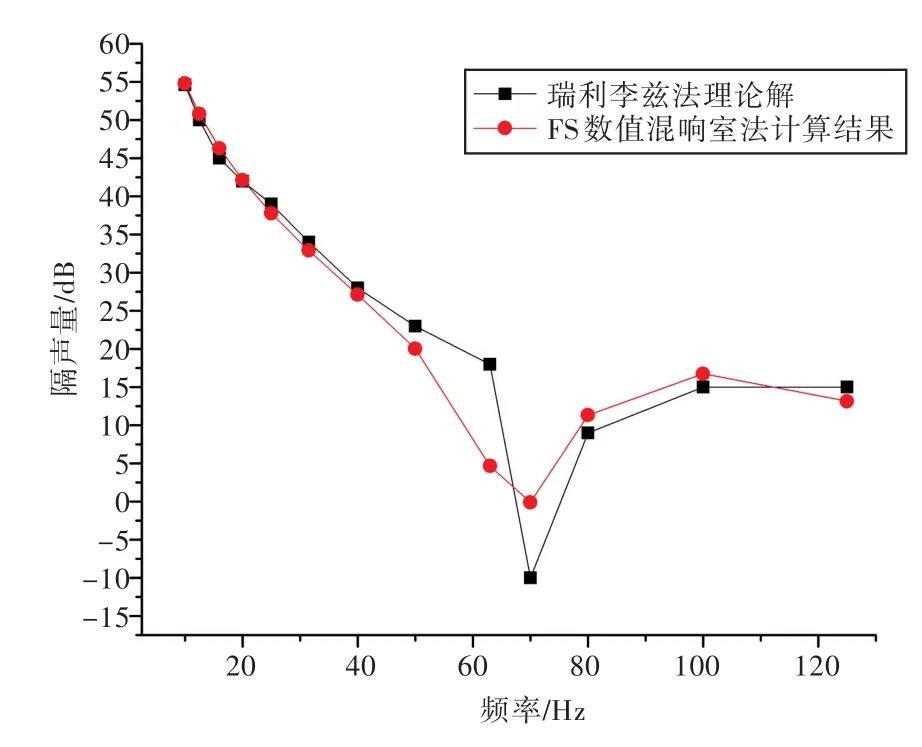
图2 低频段(125 Hz以下)FS数值混响室法模型验证Fig.2 The modal validation of FS numerical reverberation method(below 125 Hz)
2.2 舱室降噪声学包设计与性能评估
采用1.2节所述的FS数值混响室模型进行声学包性能分析。本文设计的声学包主要用于船舶舱室降噪,选用钢板作为衬板,尺寸为350 mm×220 mm×7 mm,弹性模量为210.0 GPa,泊松比为0.3,密度为7.8×103kg/m3,损耗系数为0.1%。半无限流场距衬板500 mm,混响声源强度取为1 Pa,声学包边界条件为四边简支约束。鉴于船舶降噪设计的主要频段为中、高频,因此计算频段取为63~8 000 Hz。分别设计8种声学包(Case 1~Case 8),声学包假设设计为7层(Layer 1~Layer 7),其材料参数和结构参数分别如表1及表2所示[12]。计算得到的8种声学包的隔声量曲线及总隔声量(Transmission Loss,TL)如图3和图4所示。
其中,Case 1和Case 2,Case 3和Case 4,Case 5和Case 6,Case 7和Case 8两两为一组,其材料设置均相同,差别在于后者在层间插入了5 mm厚的空气层。也即Case 1,Case 3,Case 5和Case 7为未加空气层的声学包;Case 2,Case 4,Case 6和Case 8为加入了空气层的声学包。
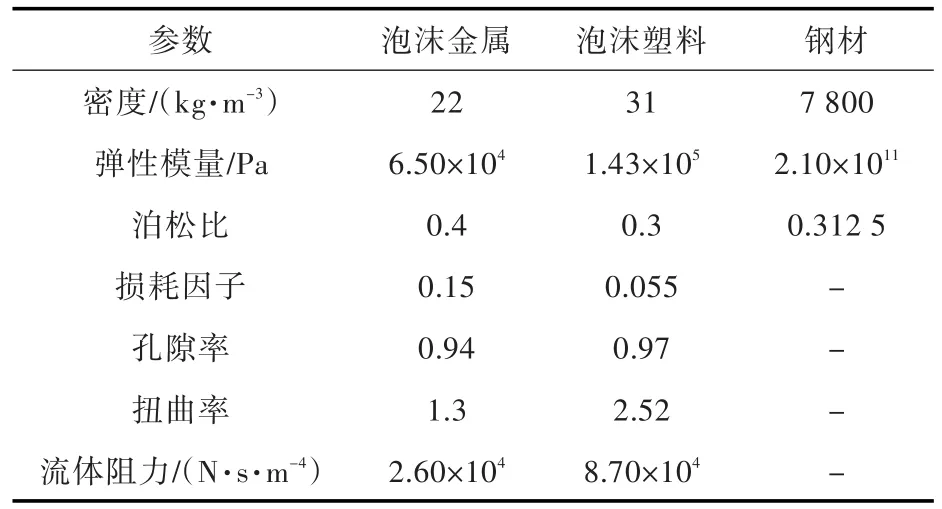
表1 8种声学包设计方案的材料特性参数Table 1 Material characteristic parameters of eight sound packages
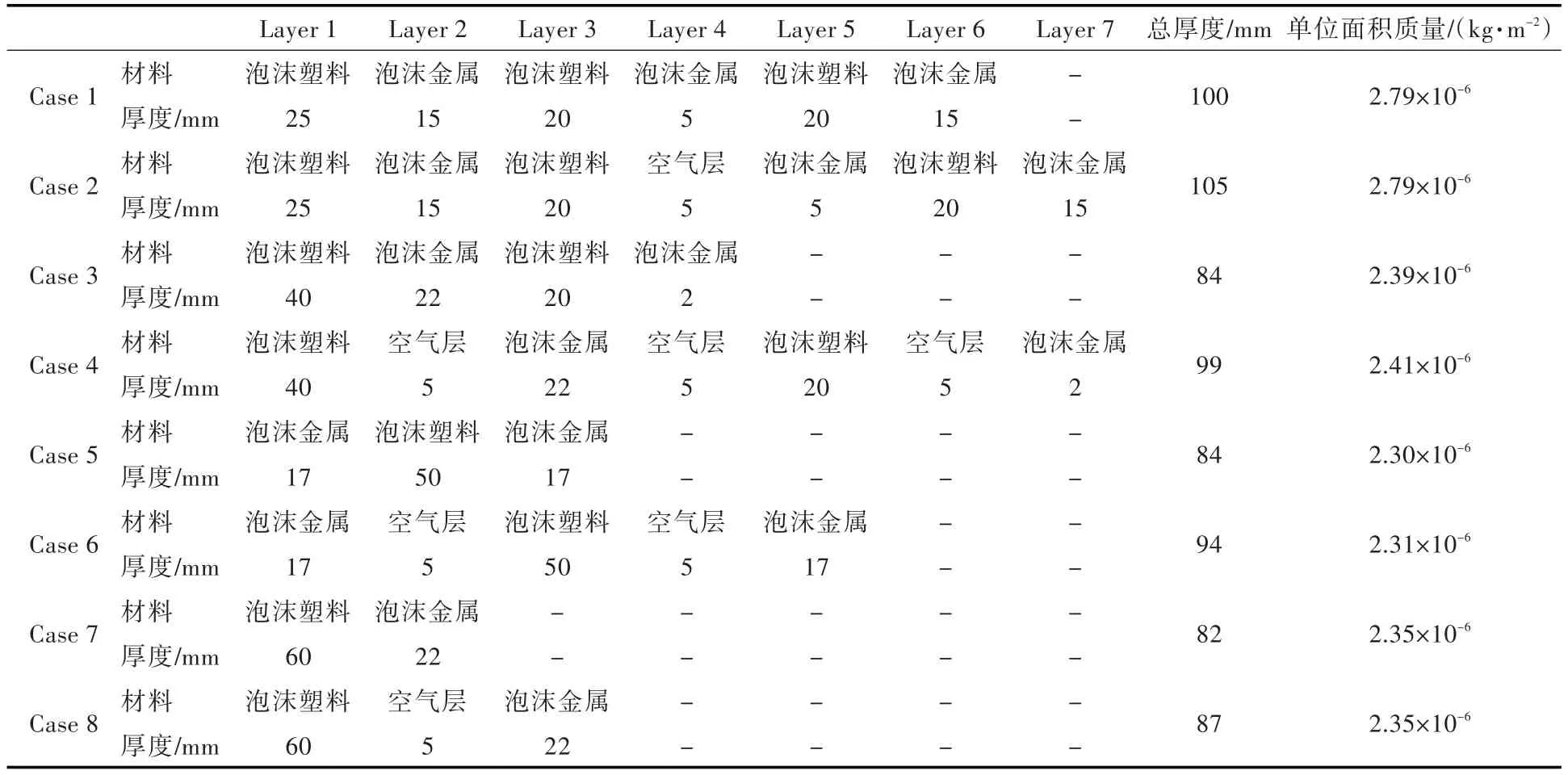
表2 8种声学包设计方案的结构参数Table 2 Structural characteristic parameters of eight sound packages
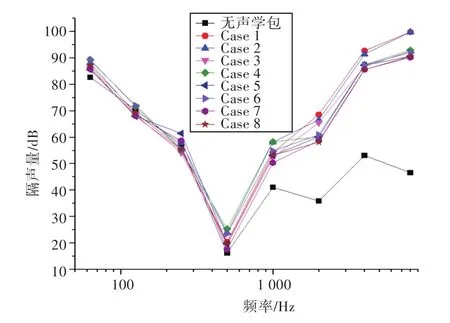
图3 8种声学包的隔声量曲线Fig.3 The TL curves of eight sound packages
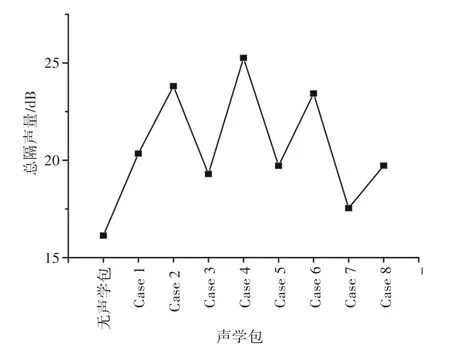
图4 8种声学包总隔声量曲线Fig.4 The overall TL values of eight sound packages
计算表明:8种声学包均可将总隔声量再提高1.5~9 dB,其中Case 4的隔声量最大,性能最佳。
3 声学包声学性能优化设计
以2.2节中的8种声学包为对象,采用遗传算法进行优化。以获得最大隔声量为优化目标,约束条件为材料层(即声学包)总厚度,声学包的材料层厚度为设计变量,变量下限为0,上限为整个声学包的厚度。按照约束条件的不同,分2种情况进行计算:优化算例1,约束设定为优化后声学包总厚度不大于原始设计厚度;优化算例2,优化后声学包总厚度不大于150 mm。
3.1 优化算例1
优化时,要求声学包的总厚度不大于原始设计的厚度。各方案优化前、后的参数对比如表3所示,优化前、后隔声量曲线的对比结果如图5所示。
表3和图5共同表明,在控制声学包厚度的基础上:
1)Case 1优化后,总隔声量上升了1.55 dB,总厚度减小了0.5mm,总重量减小了0.36×10-6kg/m2;Case 2优化后,总隔声量整体上升了22.56 dB,和初始设计相比提高了94.8%,总厚度减小了3.1 mm,重量降低为原始设计的34%;Case 3优化后,总隔声量整体上升了1.38 dB,厚度减小了0.41 mm,重量与初始设计时的基本相同;Case 4优化后,总隔声量整体上升了18 dB,和原始设计相比提高了71%,厚度减小了0.1 mm,重量降低为原始设计的34.8%;Case 5优化后,总隔声量整体上升了1.23 dB,厚度减小了7.32 mm,重量减小了0.4×10-6kg/m2;Case 6优化后,总隔声量整体上升了20.36 dB,和原始设计相比提高了86.9%,厚度减小了5.21 mm,重量变为原来的34%;Case 7优化后,总隔声量整体上升了1.68 dB,厚度减小了0.75 mm,重量和原始设计相比略有增重;Case 8优化后,总隔声量整体上升了19.87 dB,和原始设计相比提高了100%,厚度减小了9.87 mm,重量变为原始设计的22.5%。
2)不含空气层声学包(Case1,Case 3,Case 5和Case 7)优化后,隔声量平均上升了1.46 dB,厚度略有减小,重量与原始设计相比大致持平,说明不含空气层声学包的声学性能会有一定的提升,但提升的潜力较小。
3)含空气层的声学包(Case2,Case 4,Case 6和Case 8)优化后,隔声量平均上升20 dB以上,和原始设计相比平均提升了88%,厚度平均减小了4.57 mm,并且由于空气层厚度的增加,使得声学包重量大幅下降,平均降低为原始设计的31.3%。由此可见,含空气层声学包的性能提升较大。
4)从优化后的结果来看,含空气层声学包(Case2,Case 4,Case 6和Case 8)在优化后空气层的厚度会大幅增加,由此可见空气层在提升声学包性能方面具有重要作用。
3.2 优化算例2
要求声学包的总厚度不大于150 mm。各方案优化前、后参数的对比如表4所示,优化前、后隔声量曲线的对比结果如图6所示。
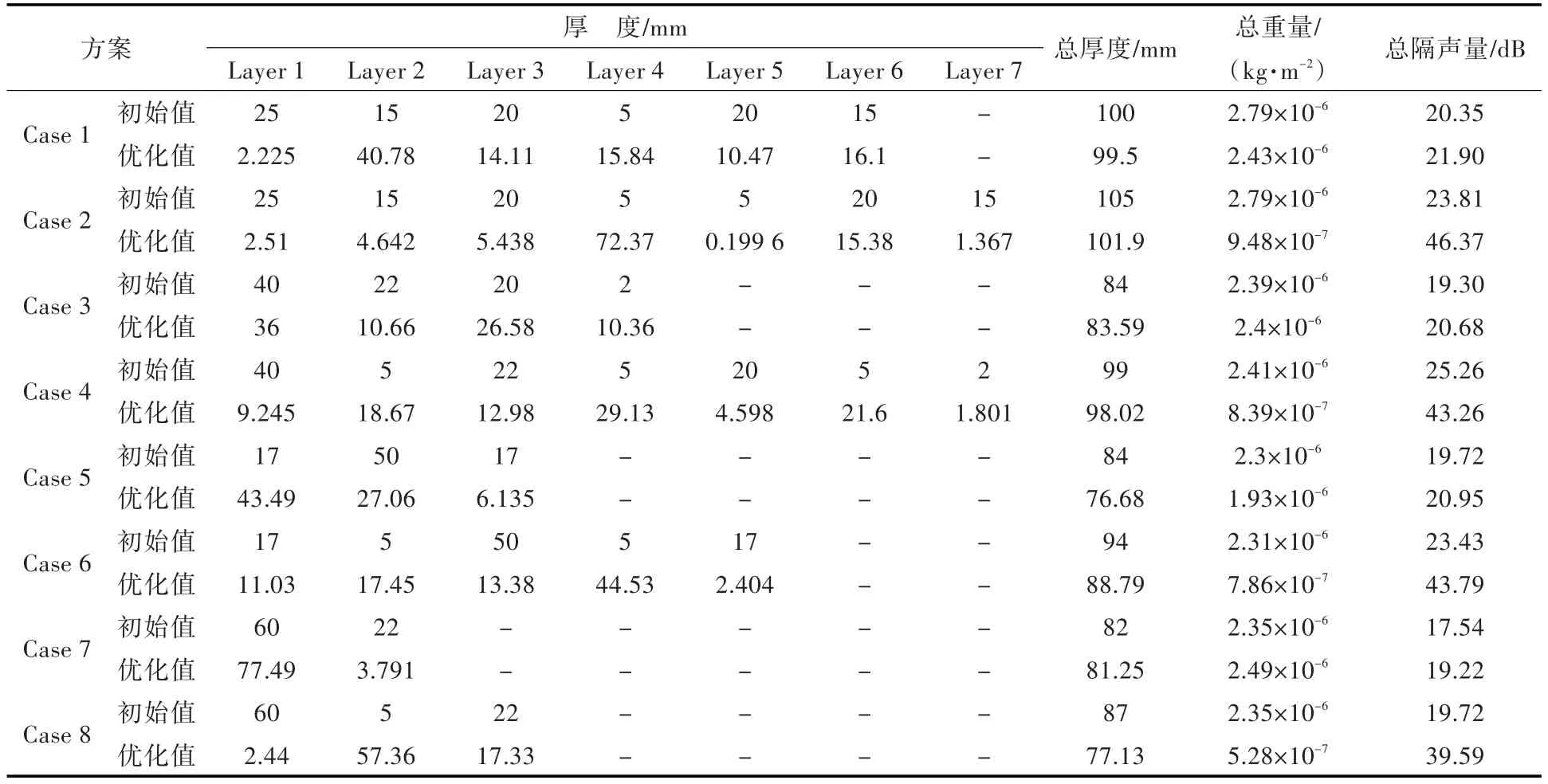
表3 Case 1~Case 8优化前后变量值对比(算例1)Table 3 Comparison of parameters before and after optimization of Case 1~Case 8 in example 1
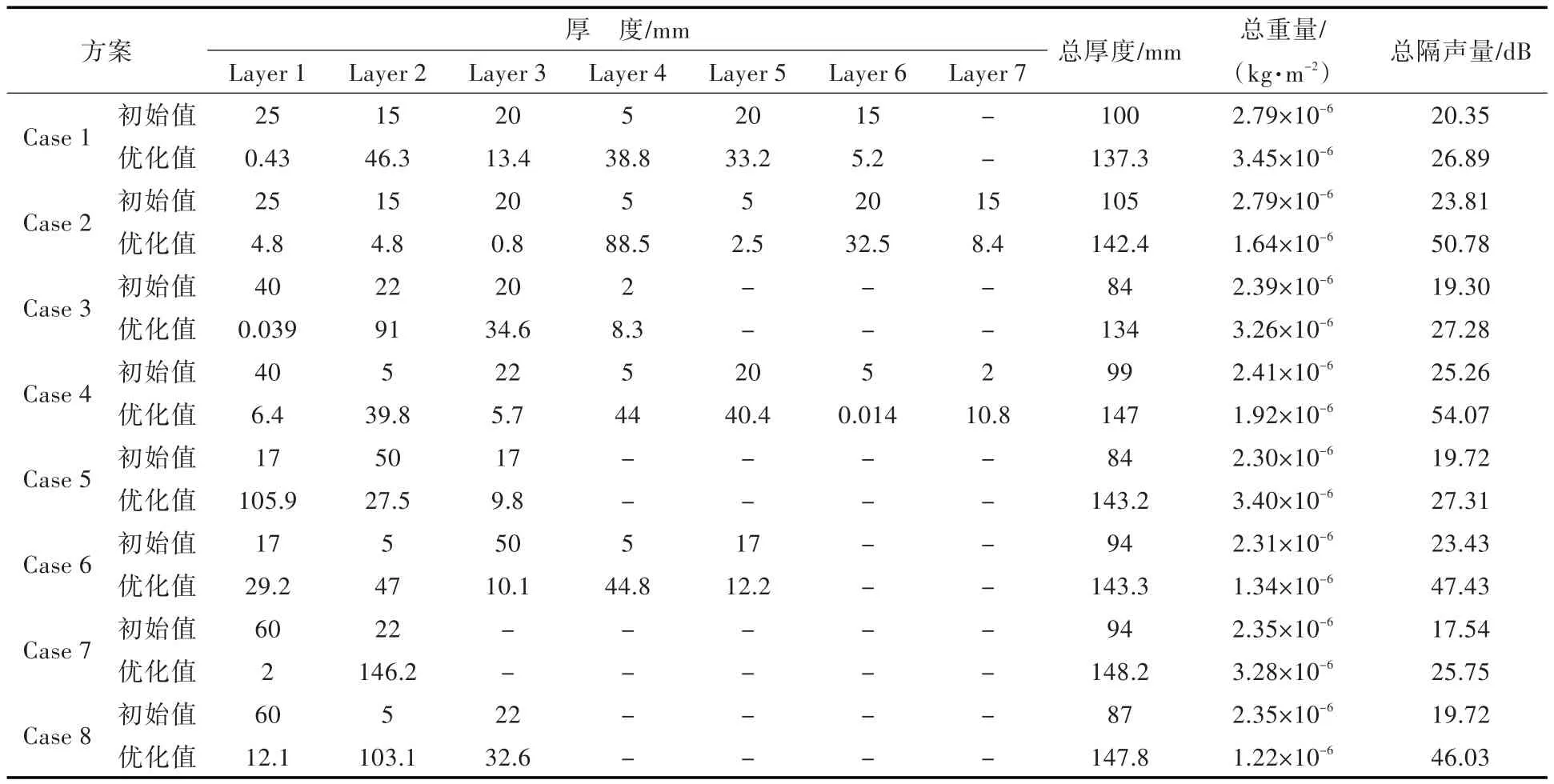
表4 Case 1~Case 8优化前后变量值对比(算例2)Table 4 Comparison of parameters before and after optimization of Case 1~Case 8 in example 2
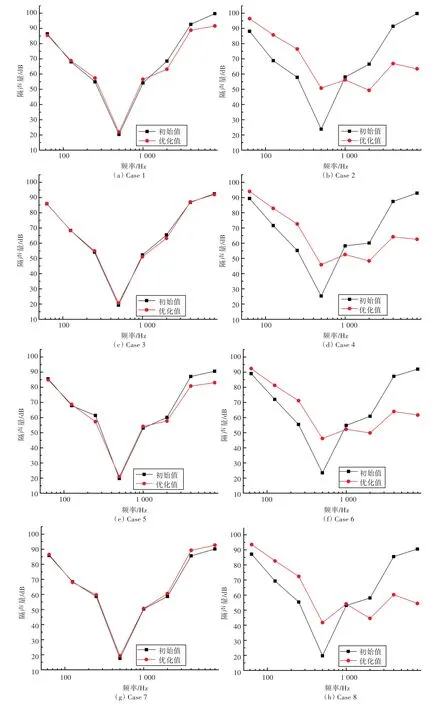
图5 Case 1~Case 8优化前后隔声量曲线对比(算例1)Fig.5 Comparison of TL curves before and after optimization of Case 1~Case 8 in example 1
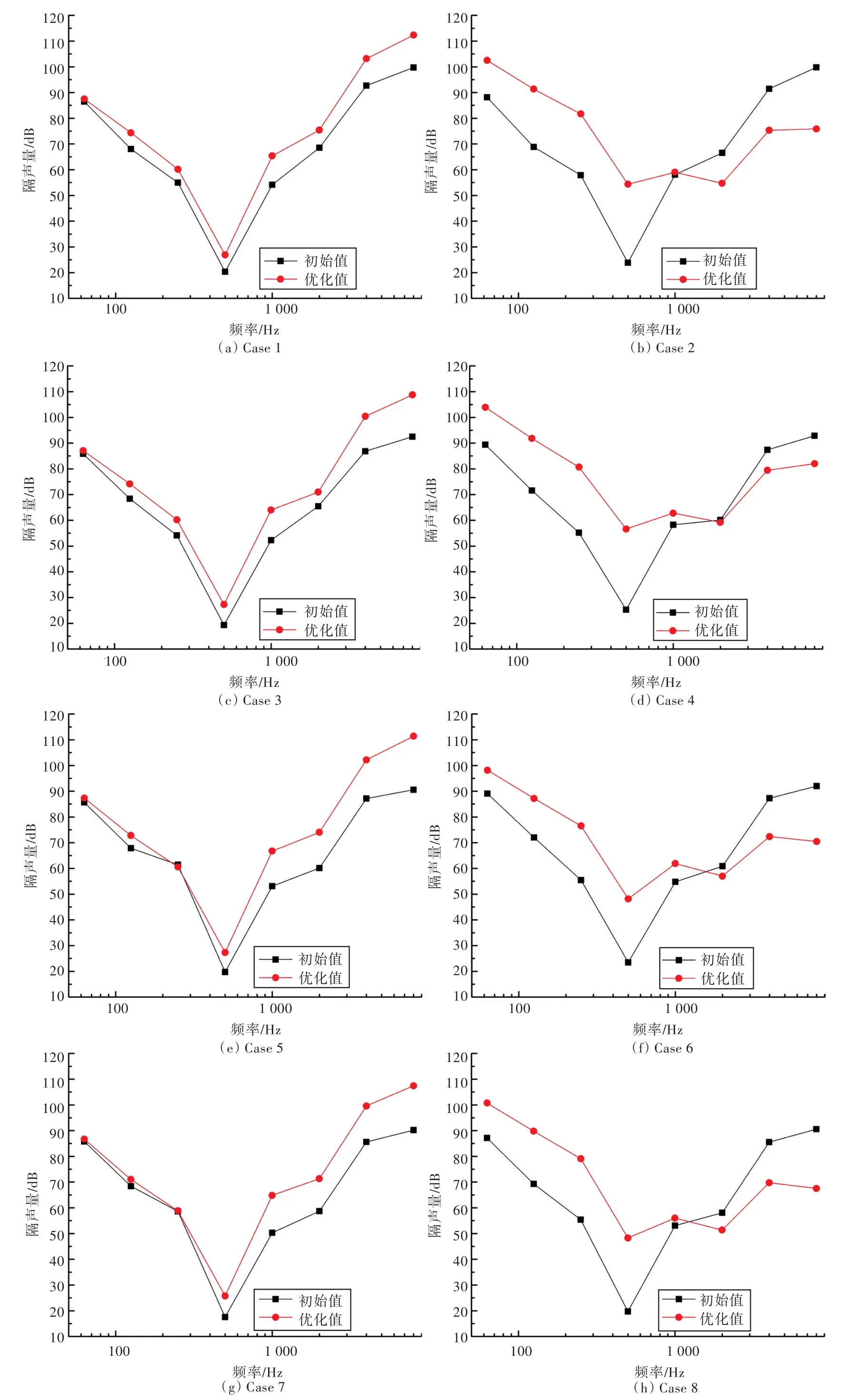
图6 Case 1~Case 8优化前后隔声量曲线对比(算例2)Fig 6 Comparison of TL curves before and after optimization of Case 1~Case 8 in example 2
表4和图6共同表明,声学包厚度控制在150 mm以内时:
1)Case 1优化后总隔声量上升了6.5 dB,厚度增加了37.3 mm,相比于初始设计重量增加了23.7%。Case 2优化后总隔声量整体上升了27 dB,厚度增加了37.4 mm,重量降低为原始设计的58.8%。Case 3优化后总隔声量上升了8 dB,厚度增加50 mm,重量和原始设计相比增加了36.4%。Case 4优化后总隔声量整体上升了28.8 dB,厚度增加48 mm,重量下降为原始设计的79.7%。Case 5优化后总隔声量整体上升了7.6 dB,厚度增加59.2 mm,重量和原始设计相比增加了47.8%。Case 6优化后总隔声量整体上升了24 dB,厚度增加49.3 mm,重量降低为初始设计的58%。Case 7优化后总隔声量整体上升了8.2 dB,厚度增加54.2 mm,相比于原始设计重量增加了39.6%。Case 8优化后总隔声量整体上升了26.3 dB,厚度增加60.8 mm,重量降低为原始设计的51.9%。
2)不含空气层的声学包(Case 1,Case 3,Case 5和Case 7)优化后,隔声量平均上升了7.6 dB,最高(Case 7)可提高8.21 dB,厚度平均增加50 mm,重量相对原始设计平均增加了36.9%。这说明当声学包厚度增加时,不含空气层声学包的性能会进一步提升;与3.1节中数据进行对比可以看出,隔声量虽然上升了约6.2 dB,但厚度增加了50 mm左右,重量增加也超过原始设计的35%以上,说明更好的声学性能是以牺牲厚度和重量为代价的。
3)含空气层的声学包(Case 2,Case 4,Case 6和Case 8)在优化后,隔声量平均上升了26.5 dB以上,最高(Case 4)可达28.81 dB,厚度平均增加了48.9 mm,但声学包的重量平均降低为原始设计的62.2%。由此可见,放开厚度约束,含空气层声学包的性能还有进一步提升的潜力。与3.1节中数据进行对比可以看出,含空气层声学包的隔声量在上升6.5 dB的同时厚度增加了48.9 mm以上,重量变为原始设计的60%以上,也是控制厚度(3.1节优化算例1)优化后重量的两倍,这说明含有空气层声学包声学性能的进一步提升也需要以牺牲厚度和重量来达到。
不同的是,相比于3.1节中的优化结果,重量有所上升,但相比于原始设计,其重量还是有大幅减小,因此当主要任务为提升性能而可以适当增加厚度时,这种优化约束也是适用的。
4 结 论
本文采用FE-SEA数值混响室法评价各声学包设计的隔声量;使用遗传算法对声学包各层材料厚度进行优化,在给定约束条件下获得声学包最优的声学性能。将算例声学包分为含空气层4种设计方案和不含空气层4种设计方案进行了性能分析及优化。研究表明:
1)当控制优化后声学包的厚度不增加时,不含空气层声学包的隔声量约可提升1.4 dB,而含空气层声学包的隔声量可提升20 dB以上,并且重量有大幅度的下降,说明含空气层声学包的性能更好。
2)当设计条件允许加大声学包厚度值时,两种类型声学包的隔声量均会进一步增加,但其厚度和重量也会上升,因此使用时需要综合考虑隔声量、厚度、重量以及造价等一系列因素。
3)FE-SEA数值混响室法可应用于全频段声学包的优化。本文给出的声学包计算分析与优化设计方法简单易行,对实际应用具有一定的参考价值。
[1]王世明.绿色船舶的现状和发展前景分析[J].中国造船,2008,49(增刊 1):48-57.WANG S M.The analysis on present situation and de⁃velopment prospect for green ship[J].Shipbuilding of China,2008,49(Supp 1):48-57(in Chinese).
[2]中国船级社.船舶及产品噪声控制与检测指南[M].北京:中国船级社,2013.China Classification Society.Guidance on noise control and testing of ships and products[M].Beijing:China Classification Society,2013(in Chinese).
[3]康洪军,蒋维钢.声学包仿真技术在高速综合检测列车降噪设计上的应用与实践[J].铁道车辆,2012,50(4):17-21.KANG H J,JIANG W G.Application and practice of the sound package simulation technology in the noise reduction design of the high speed comprehensive in⁃spection trains[J].Rolling Stock,2012,50(4):17-21(in Chinese).
[4]SAHA P.Future trends in the automotive sound pack⁃age industry[J].The Journal of the Acoustical Society of America,2001,109(5):2368.
[5]范明伟.高速船舱室噪声的统计能量分析与降噪优化研究[D].武汉:武汉理工大学,2012.FAN M W.Prediction and optimization of cabin noiseof high-speed ship based on statistical energy analysis method[D].Wuhan:Wuhan University of Technology,2012(in Chinese).
[6]高处.船舶舱室声学优化设计理论与方法研究[D].上海:上海交通大学,2015.GAO C.Optimization theory and methods of ship cab⁃ins acoustics design[D].Shanghai:Shanghai Jiao Tong University,2015(in Chinese).
[7]苏朝勇.基于VA One的声结构优化系统的二次开发[D].大连:大连理工大学,2009.SU Z Y.Secondary development of structural vibra⁃tion-acoustic optimization based on VA One[D].Da⁃lian:Dalian University of Technology,2009(in Chi⁃nese).
[8]石嘉欣,杨德庆,郁扬.隔声量计算的边界元—有限元—统计能量法[J].噪声与振动控制,2016,36(6):62-66.SHI J X,YANG D Q,YU Y.BEM/FEM/SEA hybrid method for sound transmission loss calculation of acoustic materials[J].Noise and Vibration Control,2016,36(6):62-66(in Chinese).
[9]COTONI V,SHORTER P,LANGLEY R.Numerical and experimental validation of a hybrid finite ele⁃ment-statistical energy analysis method[J].The Jour⁃nal of the Acoustical Society of America,2007,122(1):259-270.
[10]LANGLEY R S,CORDIOLI J A.Hybrid determinis⁃tic-statistical analysis of vibro-acoustic systems with domain couplings on statistical components[J].Jour⁃nal of Sound and Vibration,2009,321(3/4/5):893-912.
[11]应申舜,卢奂采,姜伟.多孔橡胶材料声传递损失性能分析:模型描述[J].轻工机械,2013,31(6):1-4.YING S S,LU H C,JIANG W.Sound transmission loss analysis of porous rubber material:descriptions of model[J].Light Industry Machinery,2013,31(6):1-4(in Chinese).
[12]SGARD F C,ATALLA N,NICOLAS J.A numerical model for the low frequency diffuse field sound trans⁃mission loss of double-wall sound barriers with elas⁃tic porous linings[J].The Journal of the Acoustical Society of America,2000,108(6):2865-2872.
Design and optimization of sound package using FE-SEA numerical reverberation method
YANG Deqing1,2,3,SHI Jiaxin1,2,3,YU Yang1,2,3
1 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China 2 State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China 3 School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China
To solve the low efficiency problem of the conventional sound package,the FE-SEA numerical reverberation method is applied in the design and optimization of sound packages in the whole frequency domain.Two types of sound package with and without air layers are designed and optimized.The FE-SEA numerical reverberation method is used to calculate sound transmission loss.The thicknesses of the air layers of the sound packages are defined as design variables.The optimization results reveal that the sound package with air layer has better acoustic performance than the one without air layers,and the sound transmission loss can be raised 2-6 dB after optimization.The research results have important guiding values for ship sound package design in actual engineering.
sound package;optimization;FE-SEA numerical reverberation method;transmission loss
U661.44
A
10.3969/j.issn.1673-3185.2017.04.005
http://kns.cnki.net/kcms/detail/42.1755.TJ.20170727.1027.028.html期刊网址:www.ship-research.com
杨德庆,石嘉欣,郁扬.基于有限元—统计能量数值混响室法的声学包设计与优化[J].中国舰船研究,2017,12(4):26-34.
YANG D Q,SHI J X,YU Y.Design and optimization of sound package using FE-SEA numerical reverberation method[J].Chinese Journal of Ship Research,2017,12(4):26-34.
2017-03-10< class="emphasis_bold">网络出版时间:
时间:2017-7-27 10:27
国家高技术船舶科研计划资助项目(2012-533);国家自然科学基金资助项目(51479115)
杨德庆(通信作者),男,1968年生,博士,教授,博士生导师。研究方向:船舶结构减振降噪理论与方法。E-mail:yangdq@sjtu.edu.cn
