3Dmax中纳米材料微观形貌模型的构建
2017-08-02袁优
袁优
摘 要:利用先进的计算机科学技术辅助材料科学研究可帮助科学工作者更好地展示自己的科研成果,让一些深刻的知识科研形象地表现出来便于理解。本文利用3D max中一些简单的建模技术,实现了空心球壳、小球组大球、六角碳骨架等结构,是科研工作中十分常用的图形。这些方法不仅仅使用于构筑以上一些结构,还可以移植到类似的结构或几种结构进行复合的情况,具有广泛的通用性。这将有利于推进计算机建模技术在构建纳米材料微观形貌模型中的更多应用。
1 引言
材料学是一门丰富且具体的学科,关于材料的微观形貌表征也是其中一块很重要的部分,这可以为探索其性质提供一些指导。常见的微观形貌表征方法有光学显微镜、电子显微镜等,这些手段已经可以较好地展现出材料的微观形貌。随着计算机技术的不断进步,更加具体形象的图形构建技术已经得到实现,使得采用计算机进行绘制各种奇异的微观形貌成为可能。
目前在各类学术论文中,通过绘制微观形貌来展现实验流程或合成产物是一种有效地表现手段。一些双层或者中空结构,利用这种3D建模的方法可以获得很好的呈现效果。另外,许多管状结构内外部的纳米材料分布情况,也可以采用这种绘制的微观形貌示意图来展现,这些为科研工作的迅速向前推进提供了一些直观、丰富的驱动力。
所以,通过利用计算机软件3D max设计和构建材料的微观形貌,从而获得更好的理解,对于科学研究的进步是很有意义的。
2 建模基本方法
三维建模的基本手段很多,在这里,我们主要想利用一些常用的复合图形的方法,将3D max中常见的几何体进行加、减及差集、并集等操作。本文想介绍的主要是一些复合或者含有空缺的结构的设计与绘制,如空心球壳,小球组大球,六角碳材料结构等等。利用到的3D max中的一些基本手段包括以下几个:
1)布尔运算
布尔运算是3D max的一种常用工具,用来将两个重合的模型去交集、并集或补集,在做模型时需要挖去或接上一部分的时候一般都用布爾运算。
2)散布
这一功能能够将两个形状各异的物体(一般是一大一小),进行无缝衔接,且小物体可通过几种不同的方式有规律地分散在大物体表面。这对于构建点缀式几何体或者由小物体组建大物体十分有效。
3)阵列
阵列其实就是让同一物体或同一组物体在某一方向或某一角度循环重复相应的次数,得到一队整齐排列的图形组。这对于构建微观结构中的大规模阵列模型十分有效
3 实例
接下来,本文通过几个实例,来具体阐述,如何利用3D max中的以上方法,来构建出不同类型的材料微观形貌,本论文采用的3D max为2012版的,其他版本的操作思路也都是相似的。
1)空心球壳结构
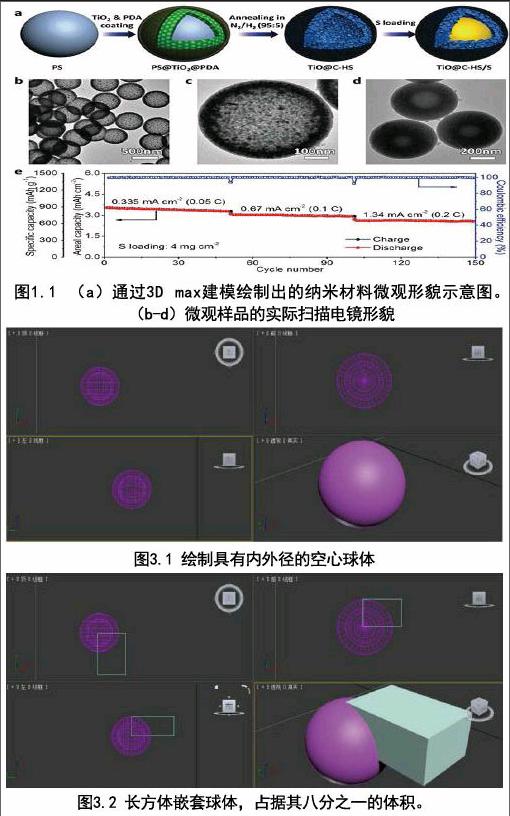
我们通过布尔运算的差集来进行绘制空心球,利用的元素都比较简单。首先我们需要做一个球体(中空),大小可以自己把握,如图3.1。这里值得注意的是,需要使用修改器中的“壳”这一工具,才能实现具有内外径的球体,即中空的球体。
接下来,我们利用一个长方体,来占据该球体右上角的八分之一的空间,实现两个几何体的有效嵌套,如图3.2所示。
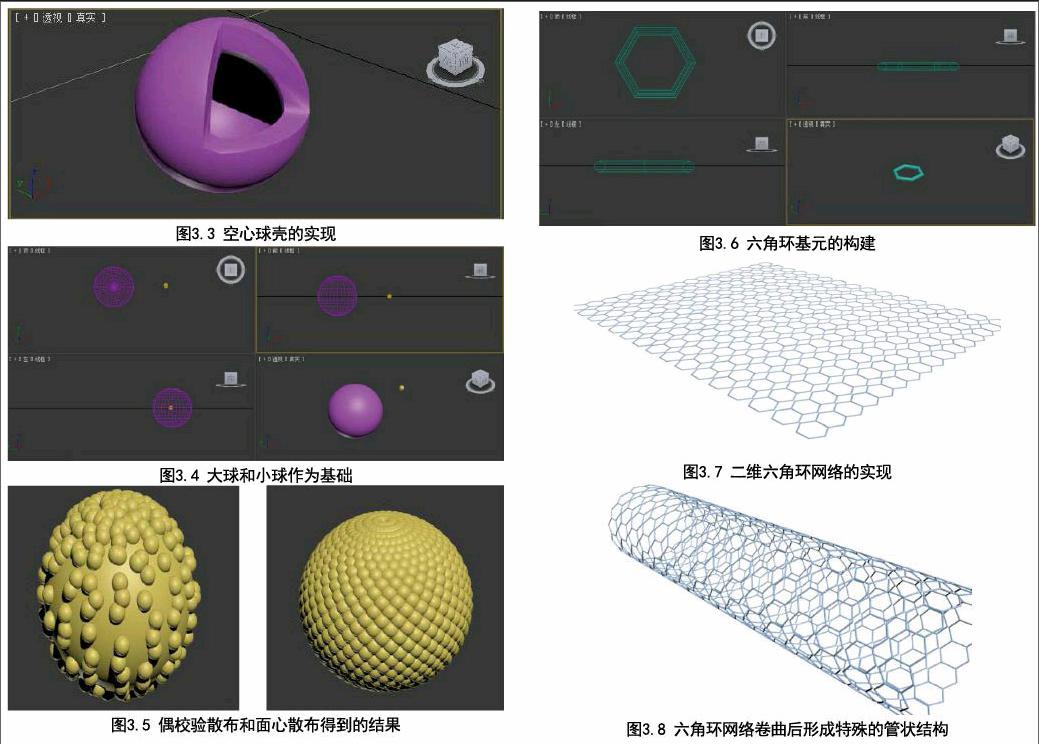
随后是最关键的一步,我们需要利用几何体对象中的复合对象,选取布尔,先选中长方体,然后拾取球体作为对象,找到差集运算,球体可以实现几何上削减去两个几何体重合的部分,如此,则可实现图3.3效果,如下图。这与文献中的示意图基本没有差别了。
2)小球组建大球结构
利用小的颗粒堆成大的几何形状是十分有趣的微观形貌,在材料科学研究过程时常出现。这里我们介绍一种比较简单的小颗粒组大颗粒的模型的构建方法,即小球组建大球的结构。
首先我们先做一个大球和小球作为基础,如下图3.4所示。
接下来,我们利用小球作为散布的基本原子,利用几何体复合对象中的散布命令,拾取大球作为对象,设置散布对象的数量及模式,将小球随机或均匀地分布在大球表面,如下图3.5。
如此我们即可构建出各种各样小尺寸几何体组成大尺寸几何体的图形,这种方法也适用于构建其他类似结构的形貌。
3)六角环组成的碳结构(如石墨烯,碳纳米管等)
碳骨架结构的六角环蜂窝煤结构,是广大科研工作者十分欣赏的一种结构,如何将该结构做大做强,实现各种热点形貌(如管状的碳纳米管等)是大家都十分关心的。
我们采用多边形绘制基础的六角环碳骨架基元,如下图3.6所示,可需要将多边形渲染选项中的“在渲染中启用”及“在视口中启用”选中,以适当调整六角环的厚度,使得立体感更强烈。
接下来,我们利用单个基元的六角环,通过阵列工具,调整x,y方向的位移距离及各自阵列重复的数目,实现二维六角环网络的构建,这也就是我们常说的单层石墨烯的结构,如下图3.7所示。
当然,我们也可以把这个网络卷起来,利用修改器中的弯曲命令,对整体进行指定方向的360°弯曲,则可实现我们常说的碳纳米管结构,如下图3.8。
4 结论
本文利用3D max中一些常用的复合工具,实现了几种常见纳米材料微观形貌的模型构建,主要有:
1)利用布尔运算实现空心球壳结构。
2)利用散布功能实现小球构建大球结构
3)利用整列的方法获得六角环网络石墨烯结构及进一步提升为管状的六角环结构。
值得一提的是,这些方法在各种形状的几何体操作中均为通用的,可根据科研工作者自己的需要和纳米材料实际的微观形貌进行适当调整即可。这是利用计算机建模技术实现丰富多彩的科学成果展示的一个有趣的尝试。endprint
