Bootstrap和Jackknife的初步认识

乔汭熙

摘要：本文总结了Bootstrap和Jackknife的相关理论知识与已有研究；利用R语言进行模拟，设计复杂抽样方案并进行抽样，对Bootstrap和Jackknife的部分性质进行了验证与解释。除此之外，本文还对Bootstrap和Jackknife估计量的性质进行了简要的介绍，并对方法的改进进行了讨论。

关键词：复杂抽样；Bootstrap；Jackknife；估计

一、发展历史与研究现状

Jackknife是由Quenouille（1949）引入的一种方法，又称刀切法。Jackknife方法的思想是，通过从原始数据集中每次删除一个数据并利用其余数据重新计算估计量，根据得到的一组估计值，可以对待估参数及其他性质进行估计。

Quenouille在1949年提出，可以通过将样本划分为两个半样本的方式，以减少序列相关的估计量的偏差。在其1956年的研究中，提出将样本量为n的样本划分为g组大小为h的样本的方法，并讨论了这种方法的可行性[1][2]。

Jackknife方法在对残差的估计（P.S.R.S Rao and J.N.K.Rao，1970）、区间估计（Tukey）、极大似然估计（Fryer，1970）等方面优良性质均已被证明[1]。

对于多元的Jackknife，Dempster在其1966的研究中，提出了一种改进的Jackknife方法，用于处理典型相关问题。Layard（1972）指出，当传统正态方法对两个协方差矩阵相等性的检验不稳健时，Jackknife方法可以很好的处理。Lachenbruch和Mickey[1]提出了U方法（实际是Jackknife方法的应用）进行判别分析。

L.B.Jaeckel提出一种无穷细分的刀切法，虽然此方法不如原始Jackknife方法实用，但却在Jackknife和稳健估计量之间建立了桥梁（1972）。

Jackknife在其他领域的应用也极为广泛。有研究者将Jackknife与自适应加权相结合，提高了多传感器有关数据处理的精确性和稳健性[3]。还有研究者将Jackknife用于测算准备电位启始时间点[4]。

Bootstrap，又被称为自举法、自助法，是由美国斯坦福大学统计系的Efron（1979）提出的一种重抽样的方法。它以原始数据为基础，即可用于参数估计，又可用于非参数估计，在进行参数估计时只依赖于已有的观测信息，是利用小样本信息构造先验分布的最理想的方法之一。

1979年Efron提出Bootstrap之初，曾因太简单而被杂志拒收，后其发表在《The Annals of Statistics》上[2]。Bootstrap方法提出之后，统计学家争相对其进行研究扩展：Hall对Bootstrap进行了Edgeworth展开；Efron和Tibshirani对Bootstrap的性质与估计方面进行了详细的理论推导与证明，讨论了其在各种复杂数据结构、回归分析、交叉验证等方面的应用；Lahiri介绍了Bootstrap在非独立数据中的应用；Shao和Tu将Bootstrap与Jackknife进行了系统的介绍与对比。

Bootstrap对独立同分布数据的研究是最早发展的一部分，Singh在此情形证明了在某些条件下Bootstrap近似比传统正态近似的收敛速度快。

对于非独立的数据，可以用块状的Bootstrap来处理，也可以使用基于变换的Bootstrap。对于块状的Bootstrap方法，主要思想是将具有相依关系的数据放在同一个单元进行重抽样，该方法由Ktinsch与Liu和Singh首先提出。Hall等人对于块状Bootstrap样本区间的划分进行了讨论。对于基于变换的Bootstrap，其思想是对非独立的数据进行变换，使其转换为独立（或近似独立）数据，其中，最常用的变换是傅里叶变换。

Bootstrap理论的基本思想、历史发展及其若干比较前沿的研究方向包括：独立同分布数据、基于模型、带有块结构、Sieve、基于变换、Markov过程、长期相依和空间数据的Bootstrap理论等[3]。现如今Bootstrap方法已广泛地应用于统计学的各个领域，成为当下最受欢迎的重抽样方法之一。

除此之外，Bootstrap方法也被广泛应用于各个领域。黎光明[5]等人在其研究中，以心理學为背景，对于正态分布、二项分布、多项分布和偏态分布的数据，对Bootstrap 方法进行校正，作点估计和方差估计，发现校正的Bootstrap 方法优于未校正的Bootstrap 方法；有学者将Bootstrap方法应用于森林系统的抽样调查，提高了初始样本的精度[6]；有学者利用Bootstrap方法，计算了考试成绩的均值、标准差、偏度与峰值，刻画了考试成绩前四阶核密度函数曲线，对各个班级学生的考试成绩情况进行了研究[7]；还有学者将Bootstrap方法应用于过度分散的泊松模型中，得到了未决赔偿准备金的预测均方误差，进一步通过随机模拟得到了预测分布，为保险业进行准备金评估提供了新思路[8]。

二、模拟仿真与结果分析

（一）模拟

本文利用R语言，采取模拟的方法进行研究，共进行1000次模拟。首先，进行二阶段抽样，第一阶段采用PPS抽样，第二阶段采用简单随机抽样，且简单随机抽样抽取的样本量相同。其次，进行分层二阶抽样，将所有的初级抽样单元按规模分层，在每一层内进行二阶段抽样。分别利用传统方法、Bootstrap和Jackknife的方法对两种方法抽取得到的样本方差进行估计和比较。对1000次模拟的结果进行汇总、比较。结果如下。由上表可见，根据Bootstrap和Jackknife的方法对抽样误差进行估计，其效果明显好于利用传统方法进行估计。而就Bootstrap和Jackknife来说，对于本研究中所使用的两种抽样方法，Jackknife方法的效果较好，Bootstrap对抽样误差估计并不是总优于传统方法。

（二）结果分析

在一致性方面，Jackknife分布估计量在非常弱的条件下是一致的。

Jackknife无法获得样本分位数方差的一致估计，但Bootstrap却可以通过选择适当的底层分布F来获得，这也是Bootstrap相对于Jackknife最大的优势之一。Jackknife无法对分布进行估计，但Bootstrap却可以。除此之外，Jackknife分布估计量的收敛率也不如Bootstrap的分布估计量那样好。

Jackknife是非参数方法，它利用的是原数据集的子集。因此，Jackknife可能不如Bootstrap估计量效率高，但是，Jackknife对模型假设的变化更加稳健。Jackknife采用比Bootstrap更系统的取样方法。因此，对于Jackknife会有更有效的计算方法。

对于方差估计，当底层分布F拖尾时，Bootstrap估计量 即使对光滑的都可能是不一致的。Bootstrap方差估计量通常向下偏的。

另外，现有的结果表明 的一致性并不涵盖广泛的统计量。 的计算通常比 更复杂。因此，对于 是光滑时的方差估计量，综合考虑理论和计算，Jackknife比Bootstrap的效果要好，且Jackknife可以很容易地扩展到多变量的情况。推荐使用Bootstrap来处理更复杂的问题，例如估计抽样分布和建立置信度等。

事实上，由于样本来自于不同的正态分布，研究利用传统方法进行估计已没有意义，无论估计的数值大小如何，均无法说明总体的情况。在这种情况下，Bootstrap和Jackknife估计的结果更为可信。本文的模拟是对均值的方差（标准差）进行的估计，无论是从渐近性、一致性还是稳健性考虑，Jackknife效果都更好，模拟的结果也与该结论相一致。

三、Bootstrap与Jackknife的缺陷

（一）Bootstrap的缺陷

（1）在对经验分布函数进行抽样时，Bootstrap样本来自于原样本，若原样本样本量很小，Bootstrap样本中必然会出现重复的样本点，多次抽样后会使概率分布集中于少数点，从而导致计算的结果远远偏离真实结果，使估计出现偏差。

（2）在分布连续的情况下，我们只能获得观测点处的分布情况，对于非观测点处的分布并无了解，据此推断出的分布很有可能偏离真实分布。

（3）在使用Bootstrap方法时，无法对分位数进行估计，对最大次序统计量、最小次序统计量自然也无法进行估计。

（二）Jackknife的缺陷

通常情况下，Jackknife方差估计量是一致的，但在一些情况下Jackknife方差估计量会出现不一致的情况。不一致性的出现主要是因为样本函数的不平滑。

（三）模拟

（1）对Bootstrap的改进

选用的均值为2、标准差为5的正态分布对Bootstrap的改进进行模拟。对最大统计量和最小统计量进行邻域的扩充并进行抽样，方法为：，。选取不同的m值，各进行1000次模拟。结果如下。

“compare”代表了在1000次模拟中，改进后的方法更优的次数。由于模拟采取小样本，所以m值应当取大一些。可以看到，随着m的增大，改进后的方法效果越来越好。模拟结果符合已有结论。

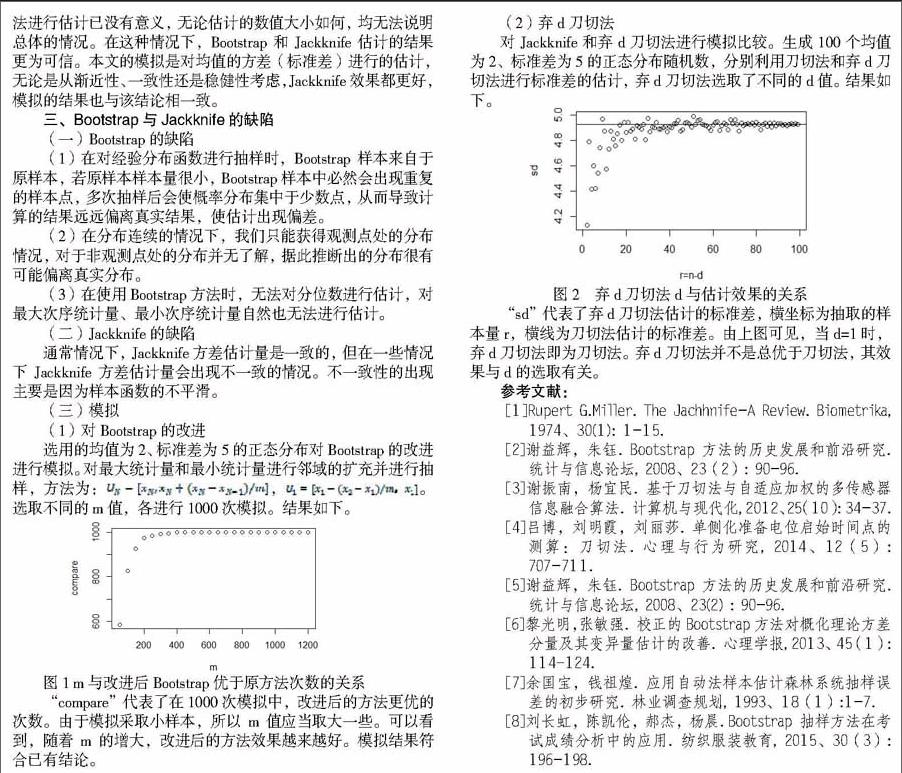
（2）弃d刀切法

对Jackknife和弃d刀切法进行模拟比较。生成100个均值为2、标准差为5的正态分布随机数，分别利用刀切法和弃d刀切法进行标准差的估计，弃d刀切法选取了不同的d值。结果如下。

“sd”代表了弃d刀切法估计的标准差，横坐标为抽取的样本量r，横线为刀切法估计的标准差。由上图可见，当d=1时，弃d刀切法即为刀切法。弃d刀切法并不是总优于刀切法，其效果与d的选取有关。

參考文献：

[1]Rupert G.Miller. The Jachhnife-A Review. Biometrika， 1974、30（1）： 1-15.

[2]谢益辉，朱钰. Bootstrap方法的历史发展和前沿研究. 统计与信息论坛， 2008、23（2）： 90-96.

[3]谢振南，杨宜民. 基于刀切法与自适应加权的多传感器信息融合算法. 计算机与现代化， 2012、25（10）： 34-37.

[4]吕博，刘明霞，刘丽莎. 单侧化准备电位启始时间点的测算：刀切法. 心理与行为研究， 2014、12（5）： 707-711.

[5]谢益辉，朱钰. Bootstrap方法的历史发展和前沿研究. 统计与信息论坛， 2008、23（2） ： 90-96.

[6]黎光明，张敏强. 校正的Bootstrap方法对概化理论方差分量及其变异量估计的改善. 心理学报， 2013、45（1）： 114?124.

[7]余国宝，钱祖煌. 应用自动法样本估计森林系统抽样误差的初步研究. 林业调查规划， 1993、18（1）：1-7.

[8]刘长虹，陈凯伦，郝杰，杨晨. Bootstrap 抽样方法在考试成绩分析中的应用. 纺织服装教育， 2015、30（3）： 196-198.