GPS与全站仪数据联合平差方法研究

李邱林，杜全维

（1.四川电力设计咨询有限责任公司，四川 成都 610016）

GPS与全站仪数据联合平差方法研究

李邱林1，杜全维1

（1.四川电力设计咨询有限责任公司，四川 成都 610016）

GPS与全站仪技术被广泛应用于各种测量控制网的建立中，研究同一个控制网中两种不同类型数据（GPS与全站仪观测数据）的平差问题十分必要。结合工作期间参加的精密工程测量项目，围绕联合平差中的若干问题展开了研究。利用参考椭球面上联合平差相关的理论和方法，运用C#语言编写了GPS与全站仪数据在参考椭球面上的联合平差数据处理软件，并通过实例论证了软件的可靠性。

GPS；全站仪；联合平差；数学模型

在高速铁路隧道（洞）CPII导线测量中，由于隧道内无法接收卫星信号，只能通过逐级布网的方式进行测量：在洞口布设加密CPI控制点，通过GPS联测CPI控制点平差计算得到坐标成果；洞内CPII导线控制点用TS30全站仪进行测量，并用GPS测量得到的加密CPI成果约束洞内CPII导线，得到CPII导线成果数据。该方法先用GPS测量加密GPI成果，再对CPII导线网进行平差计算，为了保证精度，只能提高洞外加密CPI控制点的精度等级；但若将洞外GPS测量数据与洞内CPII导线数据进行联合平差，则削弱了逐级平差带来的误差，精度更高。

对于含有GPS与全站仪两类数据控制网的平差处理，理论上有两种模式：逐级平差和联合平差。逐级平差模式，受原始数据误差影响，将降低全网精度，平差结果真实性受到影响；联合平差模式可以解决逐级平差模式中的问题，数据处理的自动化程度更高。逐级平差模式中GPS与全站仪数据采用两次平差：独立定权和分配偶然误差。联合平差模式中两类数据采用赫尔默特方差分量估计方法定权，权的确定更为科学，精度评定更为客观。联合平差的关键问题是平差方法的研究和数学模型的建立。

1 联合平差的数学模型

1.1 概述

目前，利用地球重力场模型求得的大地水准面差距N精度有限，很难获得满意结果。鉴于此，工程测量中，为了避免求取高精度的大地水准面差距N，联合平差多数在二维坐标系中进行[1-2]，既可在高斯平面（或某种工程施工坐标平面）上，也可在参考椭球面上进行。高斯平面的坐标系，适用于小范围联合平差；参考椭球面适用于高精度、大范围联合平差[3-5]。

借鉴高斯平面上联合平差的思路，本文参考椭球面上联合平差的思路为：首先按照一定数学关系式将联合平差的观测数据归算到参考椭球面上，在参考椭球面上建立联合平差观测量的误差方程和固定量约束方程，再确定其随机模型，最后进行平差和精度评定，得到适宜工程测量需要的成果。

1.2 数学模型推导

将空间网和地面网观测值统一到同一参考椭球面上，建立联合平差数学模型，主要是将地面全站仪观测元素归算为参考椭球面上的对应元素[6-8]。

1.2.1 GPS基线向量观测值误差方程

GPS基线向量观测值误差方程与三维参心大地坐标系的关系式相同。固定大地高为H，从而将GPS基线向量三维网(B,L,H)转化成只有(B,L)的二维网。

约束条件为：

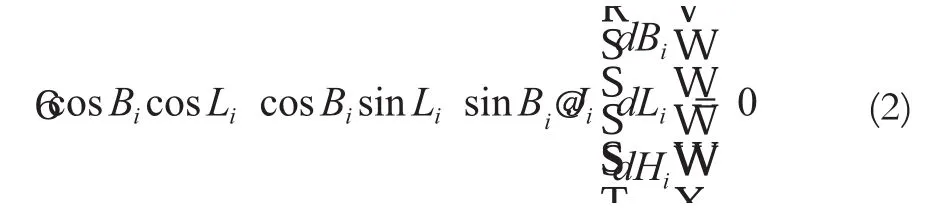
1.2.2 全站仪观测值误差方程

能够表示大地线两端的大地坐标(Bi,Li)，(Bj,Lj)，正反方位角Aij、Aji，大地线长S的微分函数关系式—赫尔默特第一类微分公式为：

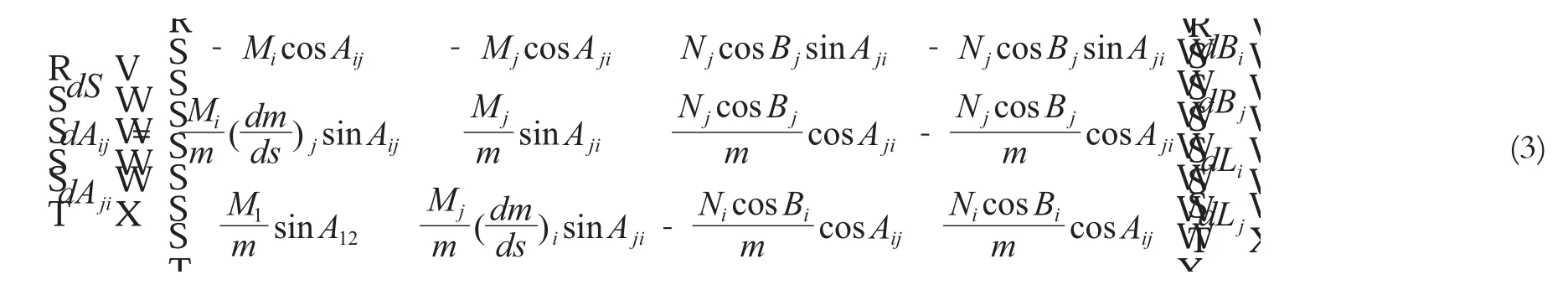
将式（3）应用于GPS基线向量网与全站仪地面网联合平差的计算，其精度是能够保证的。通过三差改正、长度归算将地面观测值归算至椭球面上。

水平方向的误差方程式为：

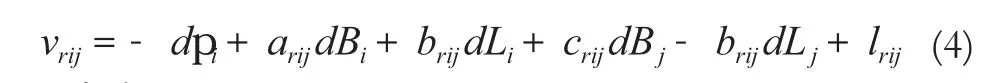
参考椭球面上的误差方程为：

综上所述，式（1）、式（2）、式（4）、式（5）为GPS与地面全站仪观测数据在参考椭球面上联合平差模型。

1.3 随机模型的确定

GPS和全站仪在参考椭球面上进行联合平差处理时，观测值种类繁多，主要包括3种： GPS基线向量观测值、全站仪角度观测值和全站仪距离观测值。联合平差时，对各类数据的定权尤为重要，定权不科学将会导致单位权方差产生偏差，并对参数估计产生影响。合理的定权不仅可以使平差结果和精度得到正确反映，对于平差模型的检验也很重要[9]。

赫尔默特简化公式为：

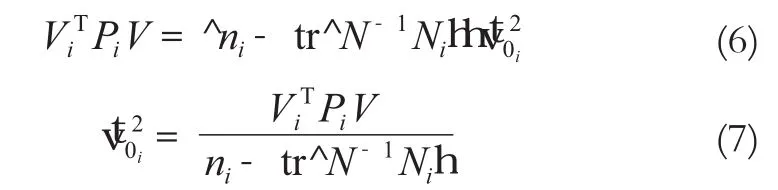
式（7）为赫尔默特方差分量估计的简化估计，通过多次迭代， 保证vt02i最后满足无偏估值。

本文中赫尔默特方差分量估计计算步骤为：

1）将联合平差数据分为GPS基线向量数据、全站仪测角数据和全站仪测距数据3类，由经验定权方法进行首次定权，确定各类观测值权的初值P1,P2,…,Pm。

2）建立误差方程进行第一次平差，求得未知量的改正数，求得ViTPiVi。

3）根据ViTPiVi，求各类观测值单位权方差估值vt02i，按照式（8）重新定权：

式中，c为常数，为了使重新定权数值便于计算，一般是选取vt02i中的某一个数值。

4）重复步骤2）、3），迭代计算直至最终平差后得到的各类观测值单位权方差估值近似相等，或通过必要的检验认为两类观测值单位权方差相等，如构造χ2统计量进行假设检验，使各类观测值单位权方差在统计意义上相等。本文的迭代停止条件为：

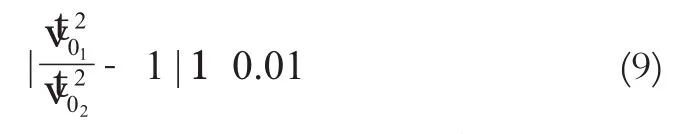
3类观测值的初始权阵定权方法为：①GPS基线向量的权阵由P=(D/σ02)-1确定，其中的D为基线解算后给出的方差-协方差阵；②边长定权由确定；③角度定权由确定，经验定权中，取σ02=1 cm2。

2 程序实现

基于联合平差理论研究和数学模型，本文编制了联合平差软件，实现了GPS与全站仪观测数据真正意义上的联合平差，其中平差使用的基线向量是在徕卡公司LGO上解算得到的，包括基线的空间信息和随机信息。

联合平差软件，界面友好，功能较完善，主要包括数据预处理、平差计算和转换工具三大模块，见图1。

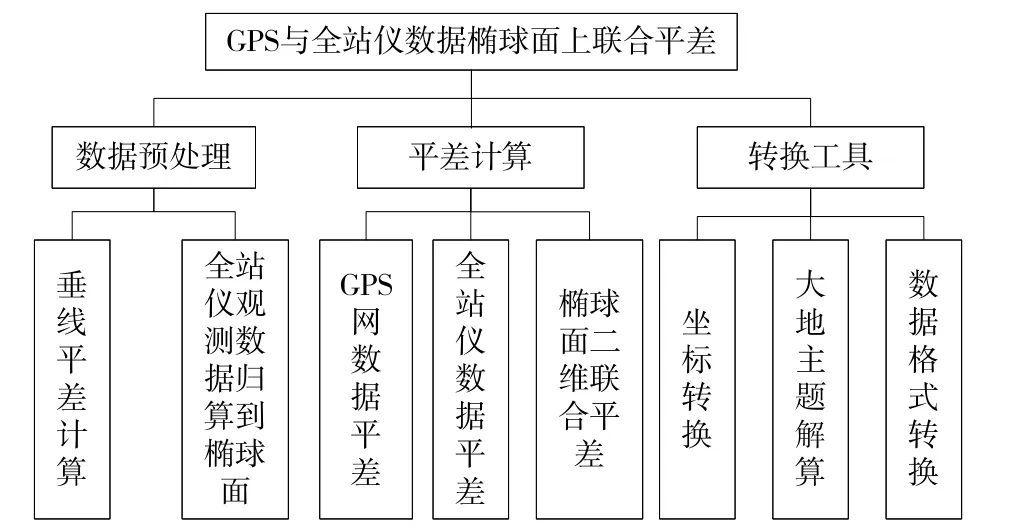
图1 程序结构图

程序中的联合平差部分未知数排序为：

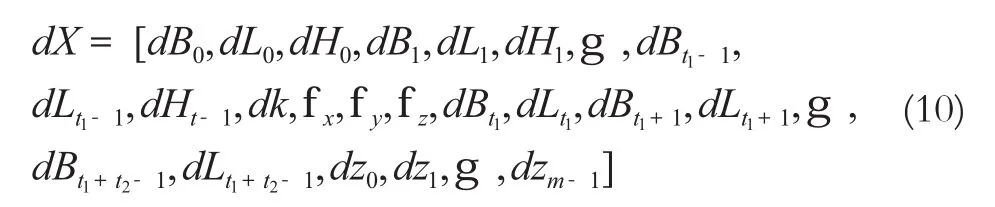
式中，(dB0,dL0,dH0)～(dBt1-1,dLt1-1,dHt1-1)为GPS网各点的未知大地坐标改正数；(dk,εx,εy,εz)为坐标旋转参数；(dBt1,dLt1)～(dBt1+t2-1,dLt1+t2-1)为地面点未知大地坐标改正数；(dz0,dz1,…,dzm-1)为地面网点改正数，采用重合点坐标误差方程将GPS网和地面网公共点联系起来。

联合平差功能部分代码为：

public void gps_union_tsd (int type_union, string path)

{

......

double m_mu = Math.Sqrt((VTPV_GPS + VTPV_TSD) / (n_ all - ATL_tsd.Length));

fi le2.WriteLine("GPS点参考坐标: " + t);

if le2.WriteLine("GPS的 VTPV: " + VTPV_GPS + " " + m_mu);

for (int i = 0; i ＜ (BLH_re_GPS.Length / 3); i++)

{

double m1 = Math.Sqrt(ATA_tsd[ij(3 * i, 3 * i)]) * m_mu;

double m2 = Math.Sqrt(ATA_tsd[ij(3 * i + 1, 3 * i + 1)]) * m_mu;

double m3 = Math.Sqrt(ATA_tsd[ij(3 * i + 2, 3 * i + 2)]) * m_mu;

file2.Write(pname_GPS[i]+ " " + af.hudu_dfm(BLH_re_ GPS[3 * i]) + " " + af.hudu_dfm(BLH_re_GPS[3 * i + 1]) + " " + BLH_re_GPS[3 * i + 2]);

fi le2.Write(" " + string.Format("{0:f 7}", m1) + " " + string. Format("{0:f7}", m2) + " " + string.Format("{0:f7}", m3));

fi le2.Write(" ");

double s0_gps = 0.0;

double s0_tsd = 0.0;

int js = 0;

TSD.dX = new double[t_tsd];

……

}

}

3 工程算例

采用某精密工程控制网的实测数据，分别利用“GPS与全站仪数据椭球面上联合平差程序1.0”与中铁第四勘察设计院编制的“铁路工程精密控制测量数据处理系统4.2.4”（SYGPS）平差结果进行分析，验证本文联合平差程序的正确性与可靠性。

联合平差软件读取GPS基线向量、全站仪数据和已知公共点数据，平差计算得到未知点的坐标，将其和SYGPS进行比较分析。联合平差软件平差结果见表 1。SYGPS平差结果见表2。二者之间的较差如图2所示。

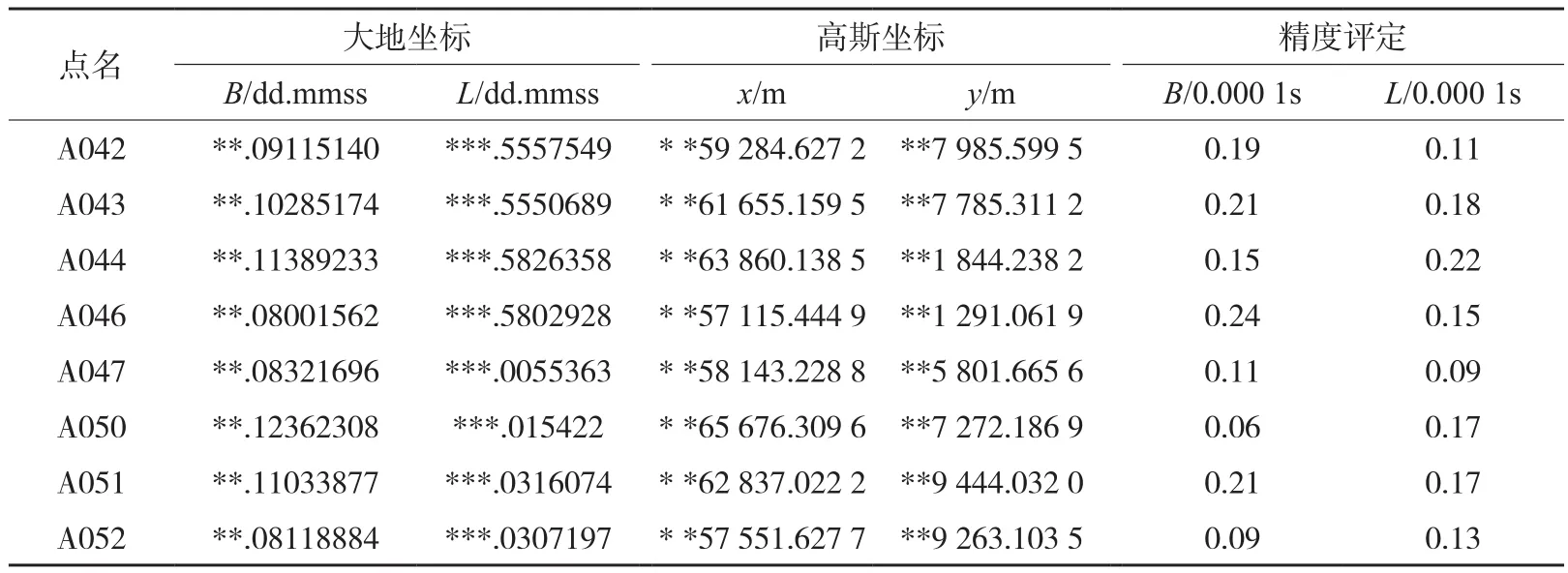
表1 联合平差软件联合平差结果

表2 SYGPS平差结果

由图2可知，两种软件计算得到的成果存在差异（0～1 m），这与平差模型、定权方式以及数据位数选取有关，总体而言，结果具有一致性，说明本文提出的方法具有较高的可靠性。

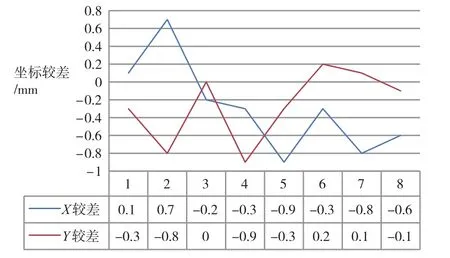
图2 两个软件平差结果较差

4 结 语

本文对GPS与全站仪数据联合平差数据处理的数学模型进行了研究，推导了在参考椭球面上联合平差的数学模型，确定了赫尔默特方差分量估计定权方法，运用C#语言，编写了GPS与全站仪数据在参考椭球面上的联合平差数据处理软件，并通过实例论证了软件的可靠性。随着科技的进步和大地测量技术的发展，不同测量仪器和测量方法将会运用于工程项目，多种数据的联合处理，是未来发展的方向；联合平差方法的研究，将会越来越广泛。

[1]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2009:300-315

[2]杨润书.GPS网与地面网的联合布设及混合平差[J].地矿测绘,1998(4):17-19

[3]张予杰,杨红艳.GPS控制网与地面网联合平差的兼容性分析[J].全球定位系统,2002(3):35-38

[4]孙腾科,华远峰.GPS与全站仪数据椭球面上的联合平差[J].测绘工程,2014,23(5):33-36

[5]卓健成,董振淑,赵秀清,等.原始数据误差对工程测量多级平面控制网精度的影响[J].西南交通大学学报,1985(1):1-12

[6]刘经南,刘大杰,桑吉章.GPS网与地面网综合数据处理商业化软件包的研制和应用[J].测绘通报,1992(5):3-7

[7]成英燕,程鹏飞,秘金钟,等.空间网与地面网联合平差数据处理方法注[J].测绘科学,2004,29(2):57-59

[8]刘大杰,刘经南,刘国辉.GPS与地面测量数据的三维联合平差[J].测绘学报,1994,23(1):14-22

[9]刘长建,马高峰.Helmert方差分量估计结果的方差一致性检验实质[J].测绘学院学报,2002,19(2):96-98

P258

B

1672-4623（2017）07-0073-03

10.3969/j.issn.1672-4623.2017.07.022

李邱林，高级工程师，主要从事工程测量方面的研究工作。

2016-08-04。