坡度分级方法对坡度制图的影响

朱奇峰, 杨勤科, 师 动, 王春梅

(西北大学 城市与环境学院, 陕西 西安 710127)

坡度分级方法对坡度制图的影响

朱奇峰, 杨勤科, 师 动, 王春梅

(西北大学 城市与环境学院, 陕西 西安 710127)

[目的] 利用多种分级方法进行坡度制图，探究不同分级方法对坡度制图带来的影响。[方法] 选取陕西省绥德县，陕西省眉县境内的秦岭山区，黑龙江拜泉县的3个样区，用多种分级法对坡度进行分级，利用量化指标分析坡度分级对坡度格局和统计分布的影响。[结果] (1) 就一个样区而言，分位数或Evans分级法比较好；不同地区比较，选用统一分级方案较好； (2) 分级后的坡度空间变异急剧减少； (3) 所有分级都使坡度信息有所损失； (4) 所有分级均难以准确表现坡度的统计分布规律。[结论] (1) 坡度表面和自然断点分级方法效果较好。(2) 随着分级间距的增加，坡度信息量快速减少。(3) 坡度统计分布的分析须用坡度表面和自然断点分级进行制图。

坡度; 坡度分级; 空间格局; 信息容量

文献参数： 朱奇峰, 杨勤科, 师动, 等.坡度分级方法对坡度制图的影响[J].水土保持通报，2017,37(3)：314-320.DOI:10.13961/j.cnki.stbctb.2017.03.054； Zhu Qifeng, Yang Qinke, Shi Dong, et al. Influence of slope classification method on slope mapping[J]. Bulletin of Soil and Water Conservation, 2017,37(3)：314-320.DOI:10.13961/j.cnki.stbctb.2017.03.054

坡度即地表任意一点切平面与水平面之间夹角的角度[1]。坡度是重要的地貌形态指标，也是坡地和流域水文、土壤侵蚀评价和太阳辐射的分析模型的重要指标[2-3]。因此坡度的研究对于坡地过程分析具有重要的意义[4-7]。坡度的研究，从空间格局和统计分析两个方面展开[8]，为此，众多学者进行了坡度制图的研究。也对坡度的分级方法进行了专门的研究[5,9-11]。随着DEM数据的积累和GIS应用的普及，基于DEM数据与GIS空间分析方法的坡度制图分析变得更加便捷。所有这些研究中也都涉及了对坡度的分级方法，但是分级方法对坡度制图结果(空间分布、统计格局等)带来什么影响，却缺乏系统分析。本研究拟选择地形起伏程度不同的3个样区，利用多种分级方法进行坡度(分级)制图，分析各种分级方法对坡度制图的影响，以期对坡度制图和分析研究提供依据。

1 数据与方法

1.1 研究样区与基础数据

本研究在3个样区展开(如图1所示)，包括地面坡度平缓、地面坡度较陡和地面坡度很陡的3个研究样区。其中地面坡度平缓的样区选择在黑龙江拜泉县，代表东北漫岗丘陵地形，样区面积549 km2，高差100.5 m，地面平均坡度2°；地面坡度较陡的样区选择在陕西省绥德县，属典型的黄土丘陵，样区面积141 km2，高差394.7 m，地面平均坡度27°；地面坡度很陡的样区选择在位于陕西省眉县境内的秦岭山区，属高起伏石质中高山，样区面积83 km2，高差2 155.9 m，地面平均坡度32°。这3个样区地形起伏由平缓到剧烈，对描述地形复杂程度的变化具有代表性。

本研究所用数据为这3个样区的10 m分辨率DEM。该数据基于1∶5万地形图、利用ANUDEM软件建立，为水文关系正确的DEM(hydrologically-correct DEMs, Hc-DEM)[12-14]，这种DEM可更好的表达地表形态及其与水文地貌要素(流水线、分水线等)的关系。

图1 研究区DEM图

1.2 研究方法

1.2.1 坡度计算 坡度的计算采用Shary[15]改进的Evans-Young算法[10]。该算法在计算p,q前对DEM做一个低通滤波处理(公式1)，然后计算pq和坡度公式〔(2)—(3)〕[15,10,6,9]。具体计算在ArcGIS中通过Python编程实现，坡度以度为单位。

(1)

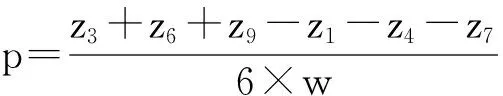
(2)

(3)

式中：p，q——高程梯度；z1到z9——分别为3×3窗口中各个像元的高程值(m)；w——像元的大小，本研究中w为10 m；Ze——滤波算法算子；θ——坡度(°)。

1.2.2 坡度分级方法 文献中常见的坡度分级方法包括：自定义分级法(SL190-2001方法、Young方法)、自然间断点分级法、标准差—均值分级法、分位数分级法。

(1) 自定义分级法。国内外有一系列坡度分级方案(Young[5],刘元保等[16];汤国安[11])，比较有影响的有：土壤侵蚀分类分级标准(SL190-2007)[17]中提出的分级方案(SL190法)和Young[5]在坡地过程研究中提出的方案。具体坡度分级级别如表1所示：

表1 SL190法与Young法坡度分级方案

(2) 自然断点分级法。以数据分布的自然断点作为分级的依据，划分原则是各级别中的变异总和达到最小[18]。

(3) 标准差—均值分级法。Evans[10]的研究认为，用坡度平均值(μ)和标准差(σ)可以推求一个6级分级系统：1级：0～(μ-1.2σ)；2级：(μ-1.2σ)～(μ-1.6σ)；3级：(μ-0.6σ)～μ；4级：μ～(μ+0.6σ)；5级：(μ+0.6σ)～(μ+1.2σ)；6级：>(μ+1.2σ)。本文中称为Evans分级法。

(4) 分位数分级法(Quantile)。是把坡度按照面积来划分，即为等面积法。根据实际需要可选择四分位、五分位、六分位…，十分位，并把处于分位数上的值作为分级值。

考虑到分级数量的对比，自然断点分级法、分位数分级法(quantile)均划分为6级。

1.2.3 坡度信息含量 本研究采用Shannon信息熵、局地方差和坡度变化率等3个指标衡量坡度信息量。

(1) 信息熵。 本研究中使用Shannon[19]提出的信息熵概念。样区坡度信息熵值越大，表明样区坡度图的信息含量越大，地形越复杂。信息熵的计算公式如下：

H=-∑pi(x)lnpi(x)

(4)

式中：H——信息熵；pi(x)——图像坡度的频率； lnpi(x)——频率的自然对数。不同的坡度分级方法

对坡度信息熵有影响。

(2) 局部方差。 局部方差平均值越大，表明数据表面的局部变化越大、表面越粗糙[20-21]。

(5)

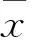
(3) 坡度空间变化率。 指坡度(坡度值或分级后每级坡度均值)在空间上的变化率，其值大小表示某种分级下坡度图空间变化的强弱。

2 结果与分析

2.1 不同分级方法坡度图的空间格局

2.1.1 图形特征 从各种分级方案下的坡度图可见(图2—3)，如果只分析一个地区的图形特征，则分位数(quantile)、Evans和自然断点等分级方案制图结果表面纹理丰富，因而效果较好，其弊端是地区之间不能比较。如果要在不同地区之间进行对比，则用统一的分类系统如SL190法、Young法。如果分析坡地过程中坡度变化、特别是坡度统计分布特征，则须用比较细的等间距分级。

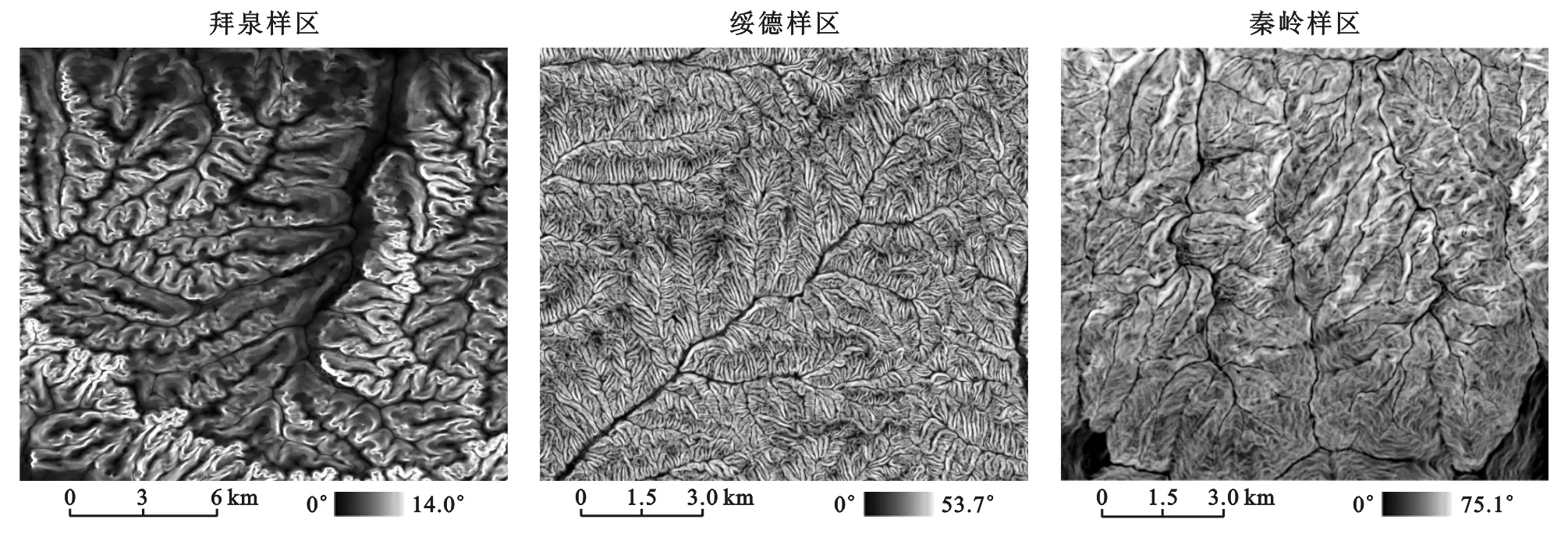
图2 研究区坡度表面

2.1.2 坡度空间变异特征 各种坡度图上的空间变化率(坡度的均值)和坡度局部方差统计表明(表2—3)，坡度分级使空间变异急剧减少。以坡度变化率和局部方差比较大的绥德样区为例，分级制图的坡度变化率和局地方差由35.23，75.35减少到3.28，0.45，分别为坡度表面的9.31%和0.60%。所以以上这几种分级方案均不适合于分析坡地发育过程中坡度的细微变化特征。可见如果要分析坡度的细微变化特征，须利用坡度表面或者比较多级的坡度分级进行制图。

2.2 不同分级方案的信息容量

2.2.1 坡度表面的信息容量 数字地形分析中坡度首先被制作为一个连续表面。为了计算其信息容量，须按照一定方案对其离散化(取整)以便得到属性表并计算信息容量。3个样区用不同离散方式，也就是使用不同的分级方式(0.1°,0.2°,0.3°,0.4°,0.5°,0.75°,1°,2.5°,5°)得到坡度分级图，并计算其信息熵表明：随着分级间距的增加，坡度信息量呈现幂函数快速减少(图4)。

注：图中1,2,3,4,5行采用不同的分级方案，分别为：SL190，Young，Evans，自然断点和Quantile。 图3 不同坡度分级图形特征表2 各种分级方案下坡度空间变化率统计均值

样区坡度表面分级方案SL190YoungEvansQuantile自然断点分级平均分级平均/%拜泉1.330.040.240.760.850.650.5138.35绥德35.232.712.383.734.023.543.289.31秦岭26.871.051.162.342.712.101.876.96

表3 各种分级方案下坡度局部方差均值

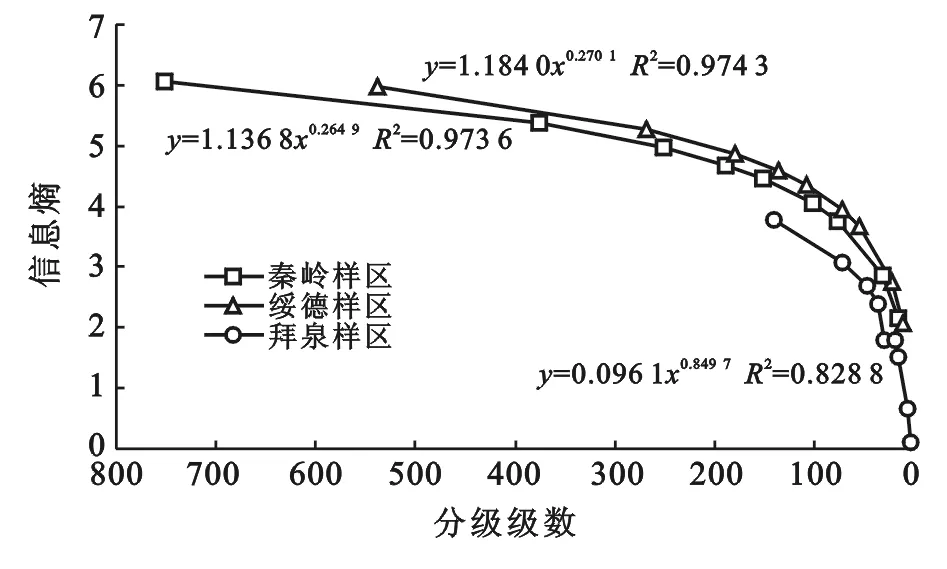
图4 等间距分级信息熵

由此可见，在坡地发育特征和坡度统计分布规律研究中，必须用足够小的分级间距实现对坡度的离散化并计算其统计特征。

2.2.2 坡度分级图信息容量 坡度分级制图中，通常划分为6～7个级别。3个样区几种典型坡度分级下坡度图的信息熵计算结果(表4)表明，在分级制图情况下，所有分级都使坡度信息有所损失，最大的为SL190法分级、最小的为分位数分级法(Quantile)分级。分位数分级法(Quantile)分级能比较好地保留坡度表面的信息量，在坡地发育过程中坡度分布特征的分析，依然得用坡度表面。

表4 各种分级方案下坡度信息熵与坡度表面信息熵比较

2.3 不同分级方法坡度图的统计分布

2.3.1 坡度表面的统计分布特征 利用1度间距等间距分级绘制坡度频率曲线(图5)并计算统计特征值(表5)结果表明，几个样区的坡度，特别是绥德(或秦岭)近似地为正态分布特征。

拜泉样区的坡度均值约为1.4°，峰值(即众数)和中值均为1°，两者都小于均值，且偏度系数为1.1，属于正偏态分布；绥德样区的坡度均值约为23.9°，峰值(即众数)和中值分别为28°和25°，两者都大于均值，且偏度系数为-0.20，属于负偏态分布；秦岭样区的坡度均值约为38.2°，峰值(即众数)和中值分别为39°和39°，且偏度系数为-0.27，两者都大于均值，属于

负偏态分布。秦岭和绥德样区偏度系数接近0，接近正态分布。

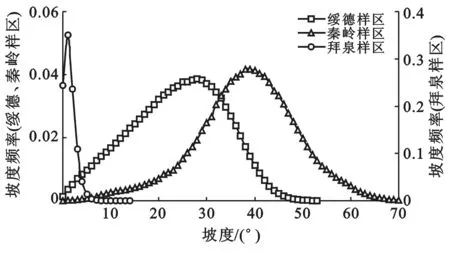
图5 坡度表面的统计分布特征(1°间隔)表5 坡度表面的统计分布特征值

样区最小值最大值平均值标准差众数中位数偏度系数峰度系数拜泉014.01.42221.23831.01.0 1.10775.0986绥德053.023.89179.710828.025.0-0.19532.4040秦岭075.038.279110.583639.039.0-0.27203.3293

2.3.2 坡度分级图的统计分布特征 坡度分级图的统计特征如图6所示，无论哪种分级方案，均不能准确表现坡度的统计分布规律。首先是不能得到统计特征值，使坡度成为了坡地类型图；其次，坡度频率曲线的形状难以体现，特别是SLP190法、Young法和quantile分级法。结合图6可见，相比之下自然断点和Evans分级方法可粗略的表现坡度的统计分布特征。这2种方法适用于成正态分布或者接近正态分布的坡度表面，制图结果能够较好反映地貌分异的规律。

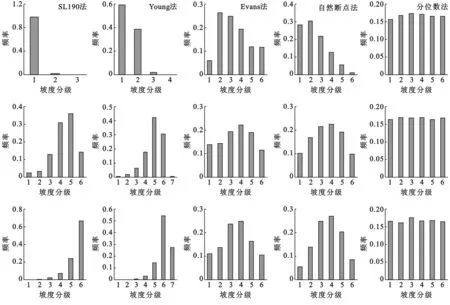
注：第1行分图为拜泉样区；第2行分图为绥德样区；第3行分图为秦岭样区。 图6 坡度分级图统计分布特征对比

3 讨论与结论

本文通过一系列定量化的指标(信息熵、局部方差、坡度变化率)，探究不同的坡度分级方法对坡度信息熵与表面格局的影响。相对于前人重点考虑分级方法[5,16]、各种分级下坡度直方图的分析[11,22]，本文通过与坡度表面的对比，从空间格局、统计分布两个方面比较全面的分析了坡度分级对制图结果的影响。与已有研究相比，本研究的主要目的是用数据来表明，在进行坡度变化特征的分析时，须用坡度表面或能表达坡度统计特征的分级方法(如自然断点分级)。本文主要研究结论为：

(1) 从空间格局看，各种分级方案均能在一定程度上表现坡度空间分布规律。就一个样区而言，分位数(quantile)分级法、Evans分级法、自然断点法比较好；不同地区比较(应用于土壤侵蚀评价或者土地资源评价等)则结合具体应用目的选用SL190或Young这些统一分级方案。但是相对于坡度表面，分级制图使空间变异急剧减少。如果要表达坡度空间变异特征，最好使用坡度表面，自然断点分级方法效果也较好。

(2) 分析坡度表面时，随着分级间距的增加，坡度信息量呈现幂函数快速减少。相对于坡度表面导出的属性表，各种分级方案下坡度图的信息容量都有很大损失。要保留最大信息量，须直接用坡度表面(比较细的等间距分级)或者分级比较多的自然断点分级方法。

(3) 任何一个地区的坡度，均有其独特的统计分布规律。这种规律只能在坡度表面上采集信息(比较细的等间距分级)，并且能得到一系列统计特征值；而分级制图则无法得到统计特征值，也无法保证固有的统计分布特征。所以研究坡度的统计分布规律，必须用坡度表面。粗略的分析可用自然断点分级法，quantile分级法和Evans分级法不能用，因为各级坡度面积会趋于相等，不能进行统计分布。

(4) 已有各种坡度分级方案，均针对特定的用途，无法形成统一的方案。同时这些分级大多针对坡地类型的研究展开，而不完全是对坡地陡缓程度的制图和分析，这在一定程度上限制了对坡度自身规律的认识。

[1] Moore I D, Grayson R B, Ladson A R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications[J]. Hydrological Processes, 1991,5(1):3-30.

[2] Wischmeier W H, Smith D D. Predicting rainfall erosion losses: A guide to conservation planning[M]∥U.S. Department of Agriculture, Science and Education Administration, Agriculture Handbook No.537, 1978.

[3] Gruber S, Peckham S. Land-surface parameters and objects in hydrology[J]. Developments in Soil Science, 2009,33(8):171-194.

[4] Carson M A, Kirkby M J. Hillslope form and process[J]. Geographical Journal, 1972,139(1):140.

[5] Young A. Slopes[M]. Edinburgh: Oliver and Boyd, 1972.

[6] Pike R J, Evans I S, Hengl T. Geomorphometry: A brief guide[J]. Developments in Soil Science, 2009,33(8):3-30.

[7] 杨勤科,贾大韦,李锐,等.基于DEM的坡度研究:现状与展望[J].水土保持通报,2007,27(1):146-150.

[8] Strahler A N. Quantitative slope analysis[J]. Geological Society of America Bulletin, 1956,67(5):571-596.

[9] Olaya V. Basic land-surface parameters[J]. Developments in Soil Science,2009,33(8):141-169.

[10] Evans I S. An Integrated System of Terrain Analysis and Slope Mapping[D]. England: Department of Geography, University of Durham, 1979.

[11] 汤国安,宋佳.基于DEM坡度图制图中坡度分级方法的比较研究[J].水土保持学报,2006,20(2):157-160.

[12] Hutchinson M F. A new procedure for gridding elevation and stream line data with automatic removal of spurious pits[J]. Journal of Hydrology, 1989,106(3/4):211-232.

[13] 杨勤科, McVicar T R,李领涛,等. ANUDEM:专业化数字高程模型插值算法及其特点[J].干旱地区农业研究,2006,24(3):36-41.

[14] 杨勤科,师维娟, McVicar T R,等.水文地貌关系正确DEM的建立方法[J].中国水土保持科学,2007,5(4):1-6.

[15] Shary P A, Sharaya L S, Mitusov A V. Fundamental quantitative methods of land surface analysis[J]. Geoderma, 2002,107(1/2):1-32.

[16] 刘元保,唐克丽.国内外坡度分级和王东沟试验区的坡度组成[J].水土保持通报,1987,7(3):59-65.

[17] 中华人民共和国水利部, SL190-2007土壤侵蚀分类分级标准[S].中国水利水电出版社:北京. 2008:8-9.

[18] Jenks G F, Coulson M R C. Class Intervals for Statistical Maps[M]. Bertelsmann C. 1963.

[19] Shannon C E. The mathematical theory of communications[J]. Bell System Technical Journal, 1948,27:379-423,623-656.

[20] Woodcock C E, Strahler A H. The factor of scale in remote sensing[J]. Remote Sensing of Environment, 1987,21(3):311-332.

[21] Drǎgut L, Eisank C, Strasser T. Local variance for multi-scale analysis in geomorphometry[J]. Geomorphology, 2011,130(3/4):162-172.

[22] 赵牡丹,汤国安,陈正江,等.黄土丘陵沟壑区不同坡度分级系统及地面坡谱对比[J].水土保持通报,2002,22(4):33-36.

Influence of Slope Classification Method on Slope Mapping

ZHU Qifeng, YANG Qinke, SHI Dong, WANG Chunmei

(CollegeofUrbanandEnvironmentScience,NorthwestUniversity,Xi’an,Shaanxi710127,China)

[Objective] A variety of slope classification methods was applied for slope mapping to explore the influence of different methods on them. [Methods] We selected three sites that are in Suide County of Shaanxi Province, Qinling Mountains in Meixian County of Shaanxi Province and Baiquan County of Heilongjiang Province as the case study areas. A variety of slope classification methods were applied to classify slope. Using the quantitative indicators, we analyzed the spatial pattern and statistical distribution characteristics of slope map. [Results] (1) For specific site mapping, quantile or Evans classification method is better; while for comparison of different sites, unified classification scheme is better; (2) Spatial variation decreased dramatically after slope was classified; (3) All slope classification methods lose some slope information; (4) All slope classification schemes were difficult to represent statistical distribution law of slope accurately. [Conclusion] (1) The slope surface and natural breakpoint methods are better; (2) With the increase of grading space, slope information declines rapidly in a power function; (3) Statistical distribution of slope is better to be mapped with slope surface and natural breakpoint methods.

slope, slope classification, space structure, information content

2017-01-12

2017-02-17

国家自然科学基金项目“地表坡度的统计分布理论模型研究”(41371274)，“黄土丘陵沟壑区侵蚀地形空间频率层次性研究”(41301284)

朱奇峰(1990—),男(汉族),陕西省西安市人,硕士研究生,研究方向为数字地形分析。E-mail:qfzhuqf@163.com。

杨勤科(1962—),男(汉族),陕西省陇县人,博士,教授,主要从事侵蚀地形分析和区域土壤侵蚀评价研究。E-mail:qkyang@nwu.edu.cn。

A

1000-288X(2017)03-0314-07

P283