基于强度折减方法的边坡稳定性极限上限分析

王作伟 黄诗阳

(长沙市中等城乡建设职业技术学校，湖南 长沙 410126)



基于强度折减方法的边坡稳定性极限上限分析

王作伟 黄诗阳

(长沙市中等城乡建设职业技术学校，湖南 长沙 410126)

结合强度折减方法和极限分析上限法理论，推导出了均质边坡安全系数的计算公式，针对隐式表达形式的安全系数计算公式，采用MATLAB序列二次优化工具箱，计算得到了边坡的安全系数，通过与传统的极限平衡法和数值模拟方法的对比，验证了该方法具有良好的适用性。

安全系数，强度折减法，边坡稳定性，岩土工程

0 引言

边坡稳定性计算是岩土工程中重要的研究问题。已有的边坡稳定性主要计算方法有：极限平衡法[1]、数值模拟方法[2]和极限分析方法[3]等。极限平衡方法是应用最为广泛的一种实用方法，且基于该方法的商用化软件也很多，例如Geoslope，理正岩土等。极限平衡法通过将边坡划分为多组土条，引入静力平衡条件和一些假设性条件，从而将静不定的求解问题转化为可解的方程组进行求解。数值模拟方法的优点是能够反映出边坡在外部因素作用下的变形影响，而缺点是计算较为复杂。极限分析方法近些年来得到广泛的关注，通过建立不同的破坏模型，可以处理诸如土质、岩质等边坡的稳定性求解。本文对极限分析方法计算和分析边坡稳定性进行一些探讨。

边坡稳定性分析中，通常采用安全系数Fs表征边坡的安全储备，Fs=1表示边坡处于极限状态。在同一计算条件下，Fs的值越大表示稳定性越高。根据安全系数的定义，发展出不同的安全系数表示方法，其中包括强度折减法、比值法和超载储备法等[4]。强度折减法是将抗剪强度参数c,φ同时按照一定的系数进行折减，从而使边坡处于极限破坏状态,此时的系数即为安全系数Fs。强度折减法只降低了边坡的抗滑阻力，也比较符合一些工程失稳现象，例如边坡失稳的重要方面是外因(降雨、地震等)造成的边坡土体强度降低而引起。比值法是将边坡抗滑能力与下滑能力之间的比值作为安全系数。比值法与强度折减法的形式基本相同，但两者的计算结果常常会有差距。此外，超载储备法是将边坡土体自重增加一定系数后，使边坡处于极限破坏状态。

当前的极限分析计算中，考虑边坡的安全系数计算方法并不多见，这使得该方法的应用受到限制。本文通过建立基于强度折减法的边坡安全系数分析方法，获得边坡的安全系数，并分析了强度参数对稳定性的影响规律。

1 极限分析方法计算安全系数

极限分析理论在文献[5]中有详细的介绍。本文选取均质土质边坡为研究对象，考虑如图1所示的破坏模式。由于土体是摩擦性材料，滑移型破坏边坡的破裂面实际上不是圆弧形的。常见的边坡整体破坏为沿某一滑移面的滑动，假定边坡的滑移面为对数螺旋线，且通过坡趾[6]。该曲线方程以极坐标表示为r=r0e(θh-θ0)tanφ，其中，φ为内摩擦角。边坡的破坏形式为：滑移体以角速度ω绕O点旋转破坏。边坡的高度为H，坡顶角度为α，坡趾角度为β，且令AB=L，OB=r0。该破坏模式通过3个变量所确定：角度θ0，θh，旋转半径r0。

极限分析上限法的原理是边坡处于极限状态时，边坡的外力功率等于内能耗散功率。通过这一等式关系建立平衡方程。下面针对如图1所示的破坏机构，计算内外功率。

1.1 外功率和内能耗散率

外力功率主要是土体自重产生。计算滑移块体ABC的自重功率表达式为：

(1)

其中，γ为土体容重，函数f1，f2以及f3分别为：

f1(θh,θ0)=1/[3(1+9tan2φ)]{(3tanφcosθh+sinθh)exp[3(θh-

θ0)tanφ]-(3tanφcosθ0+sinθ0)}

(2)

f2(θh,θ0)=L/(6r0)(2cosθ0-L·cosα/r0)sin(θ0+α)

(3)

f3(θh,θ0)=1/6exp[(θh-θ0)tanφ][sin(θh-θ0)-Lsin(θh+

α)/r0]{cosθ0-Lcosα/r0+cosθh·exp[(θh-θ0)tanφ]}

(4)

根据图1中的几何关系，可以得到：

H/r0=sinβ/sin(β-α){sin(θh+α)·

exp[(θh-θ0)tanφ]-sin(θ0+α)}

(5)

L/r0=sin(θh-θ0)/sin(θh+α)-sin(θh+β)/[sin(θh+α)·

sin(β-α)]{exp[(θh-θ0)tanφ]sin(θh+α)-sin(θ0+α)}

(6)

边坡阻挡下滑的能力主要来源于滑移面上的抗滑力。内能耗散功率也就与滑移面上的剪切力和滑移面的形状有关。在整个滑移面上积分，总的内能耗散功率表达式如下：

(7)

至此，边坡失稳的极限状态方程可以根据外力功率和内能耗散功率相等的条件获得，即W=D。

1.2 安全系数表达式

强度折减法的安全系数表达式如下：

cf=c/Fs,φf=arctan(tanφ/Fs)

(8)

通过对强度参数进行折减，使边坡稳定性处于极限状态，即折减后的强度参数满足极限状态方程。结合式(1)，式(7)和式(8)，安全系数表达式如下：

(9)

其中，f1,f2,f3以及H/r0由式(2)～式(5)表示。对于安全系数的求解是最优化问题，变量为θ0,θh。值得注意的是，式(9)中tanφf也包含有Fs。通常可以采用二分法多次试算获得Fs的最小值。本文将该问题的求解转化为有约束的最优化问题，采用MATLAB的序列二次优化法进行计算，从而提高计算效率。其优化的目标函数及约束条件的表达式如下：

(10)

2 计算结果对比与分析

如前文所述，传统上一般采用强度折减法和抗滑力与下滑力的比值法来获得边坡的安全系数。在极限分析中，同样也可以采用的强度折减法和比值法(内能耗散功率与外力功率之比)来获得。下面通过算例说明，在极限分析中，强度折减法得到的安全系数更具有普遍意义。选取计算边坡模型为：高度H=10 m，坡角β=45°，上坡坡角α=0°，重度γ=20 kN/m3，抗剪强度如表1所示。极限平衡法采用Geoslope计算软件(Morgenstern-Price法)，数值模拟方法采用FLAC3D计算软件。计算结果如表1所示。

从表1可以看出，比值法在安全系数小于1时，安全系数小于强度折减法的结果，而在安全系数法大于1时，则大于强度折减法的结果，其规律也能够反映出稳定性的变化情况。另一方面，强度折减法中，数值模拟的计算结果要小于其他方法。

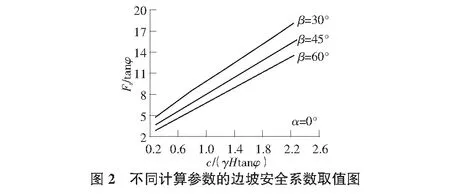
此外，通过计算发现，除边坡坡脚外，其余计算参数与安全系数在一定范围内大致呈线性变化。在相同坡脚情况下，计算参数γ,H,c,φ所组成的关系式与安全系数Fs相对应，如图2所示。对于均质边坡，可以按照图2直接查询边坡的安全系数值,例如，计算参数：β=45°，γ=18 kN/m3,H=15 m,c=28 kPa,φ=16°，则c/(γHtanφ)=0.36，对应的Fs/tanφ=4.12，即可得到Fs=1.18。

3 结语

本文结合强度折减法和极限分析上限法，推导了边坡安全系数的计算公式。针对隐式形式的安全系数表达式，通过MATLAB的最优化工具箱，计算得到了均质边坡的安全系数。主要结论如下：

1)通过分析几种不同计算方法的安全系数计算结果，说明了基于强度折减法的极限分析方法是可行的。强度折减法的意义更为统一，因此，建议采用强度折减法作为最终的计算依据。

2)计算发现均质边坡中，除边坡坡脚外，其余计算参数与安全系数在一定范围内大致呈线性变化。文中给出了均质边坡的安全系数取值图表，可以根据参数取值，直接获取安全系数的值。

[1] 戴自航,沈蒲生.土坡稳定分析普遍极限平衡法的数值解研究[J].岩土工程学报,2002,24(3):327-331.

[2] 康 平,穆 伟,汪子杰,等.基于强度折减法的某公路边坡稳定性数值模拟[J].土工基础,2012,26(3):47-49.

[3] 石挺丰,赵炼恒.基于强度折减技术的加筋路堤稳定性极限上限分析[J].铁道科学与工程学报,2011,8(2):40-46.

[4] 刘 杰,建 林,王乐华,等.三种边坡安全系数计算方法对比研究[J].岩石力学与工程学报,2011(S1):2896-2903.

[5] 陈惠发.极限分析与土体塑性[M].北京：人民交通出版社,1995.

[6] Michalowski R L..Stability Charts for Uniform Slopes[J].Journal of Geotechnical and Geoenvironmental Engineering, 2002,128(4):351-355.

Upper-bound limit analysis of the slope stability on the basis of strength reduction method

Wang Zuowei Huang Shiyang

(ChangshaVocationalSchoolofMedium-SizeUrban-RuralBuilding,Changsha410126,China)

Combining with strength reduction method and upper-bound limit method theory, the paper induces the homogeneous slope safety coefficient calculating formula. In light of hidden-style expression form security coefficient calculating formula, it applies MATLAB secondary optimizing instrumental box, calculates the slope security coefficient, and testifies its good applicability by comparing it with traditional limit equilibrium method and numerical simulation method.

security coefficient, strength reduction method, slope stability, geotechnical engineering

1009-6825(2017)18-0056-02

2017-04-11

王作伟(1985- )，男，工程师，讲师； 黄诗阳(1990- )，女，工程师

TU413.62

A