基于模糊失效概率的输气站场收球区定量风险评价研究

李平，张锦伟，税旭东

1.中国石化川气东送天然气管道有限公司（湖北武汉430020）2.中国市政工程西南设计研究总院有限公司燃气热力设计研究院（四川成都610081）

基于模糊失效概率的输气站场收球区定量风险评价研究

李平1，张锦伟2，税旭东1

1.中国石化川气东送天然气管道有限公司（湖北武汉430020）2.中国市政工程西南设计研究总院有限公司燃气热力设计研究院（四川成都610081）

针对目前国内缺乏输气站场风险因素客观失效概率的问题，提出采用模糊失效概率来确定输气站场风险因素的失效概率。该方法以专家判断为基础，采用模糊集理论将专家判断结果转化为模糊失效概率。以人员受伤面积作为失效后果评价指标，从而计算出风险值，并提出风险等级划分方法。最后对达化输气站收球区进行风险评价，其评价结果与实际风险程度一致。

输气站场；风险区块；定量风险评价；模糊失效概率；失效后果

目前站场风险评价较通用的方法有定性评价方法、半定量评价方法和定量评价方法[1-4]。定性和半定量评价方法主要是基于专家判断的风险评价，带有很强的主观性；定量评价方法是基于客观失效概率的风险评价方法，评价结果客观，但目前国内输气站场缺乏完备的风险因素的失效概率。针对3种评价方法的特点，提出采用模糊失效概率来确定输气站场风险因素的失效概率。该方法以专家判断为基础，采用模糊集理论将专家判断结果转化为模糊失效概率。以达化输气站为例，首先将站场进行风险区块划分[5]，然后对各风险区块进行风险评价。以收球区为典型风险区块，对其进行定量风险评价，验证提出的风险评价方法的正确性，对其余风险区块的风险评价具有借鉴作用。

1 输气站场收球区失效故障树分析

1.1 建立收球区失效故障树

故障树分析由美国贝尔电话研究所提出，以所研究的故障作为顶事件建立故障树，分析其中间事件和基本原因事件，用逻辑关系将事件连接，该方法能深入地揭示可能造成事故的各种因素。结合达化输气站收球区实际情况，建立了收球区失效故障树，如图1所示，其中收球区失效底层事件符号说明见表1。

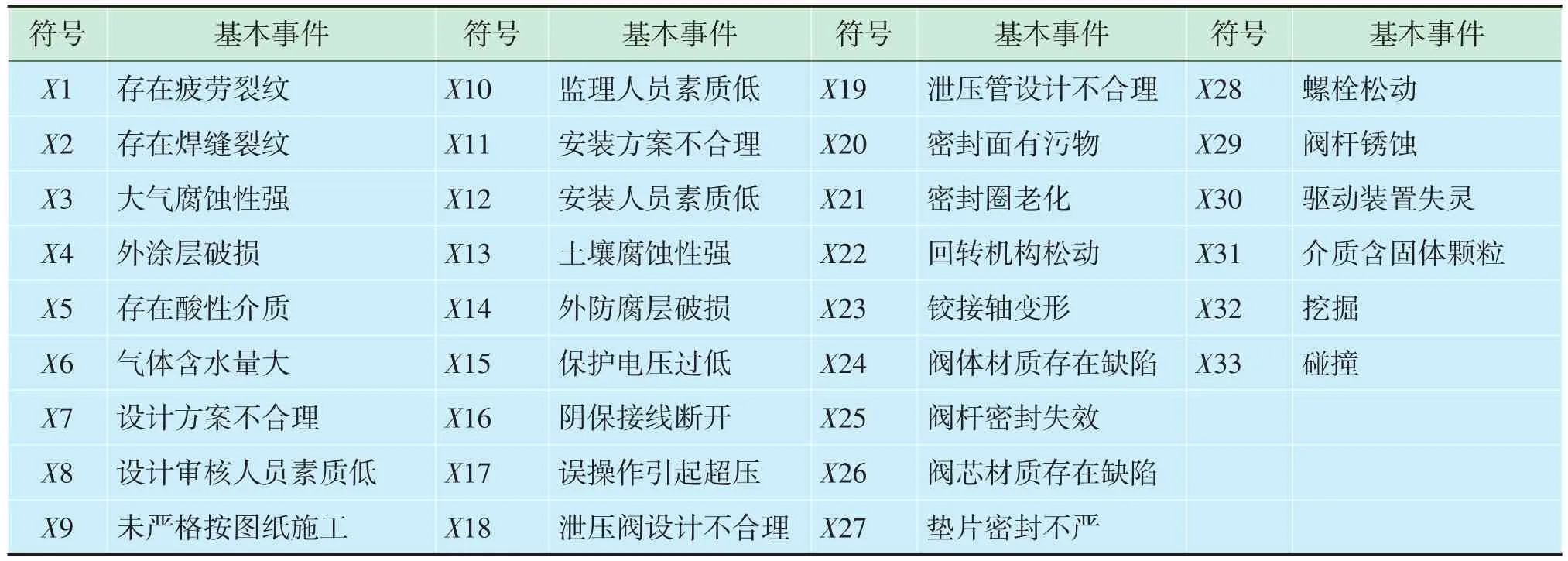
表1 收球区失效底层事件符号说明

图1 收球区失效故障树

1.2 故障树最小割集

故障树最小割集是指导致故障树顶事件发生的最小原因事件的集合。利用布尔运算原理，可将收球区失效故障树转化成最小割集的布尔代数方程：

T=X1+X2+X3X4+X5X6+X7X8+X9X10+X11X12+X13X14(X15+X16)+X17(X18+X19)+

2 输气站场收球区定量风险评价

首先对专家个人能力进行权重赋值，再将专家判断评语转化为模糊数，从而计算出故障树底层事件的模糊失效概率[6]，再根据故障树的逻辑关系计算出顶层事件失效的概率值。失效后果分析采用API 581的计算方法，以人员受伤面积作为评价指标，由模糊失效概率与失效后果计算风险值，从而确定风险等级。

2.1 模糊失效概率计算

2.1.1 专家权重的确定

采用参考文献[7]中确定专家权重的方法，根据专家情况，采用强制比较法对其进行赋值，并求出各位专家的重要度权重。

2.1.2 计算平均模糊数

由于专家不可能准确估计出原因节点的概率，所以采用自然语言进行评判，自然语言分类越细，则专家评判结果与实际情况越接近，但并不意味着分类越细越好，过细的分类会使专家难以判断。因此，本文设定“很小（VL）、小（L）、较小（FL）、中等（M）、较大（FH）、大（H）、很大（VH）”7个判断等级，以三角形或梯形模糊数代替上述自然语言，如图2所示。三角形模糊数表示为A=（a，b，c），其隶属度函数[8]为：

图2 代表自然语言的模糊数

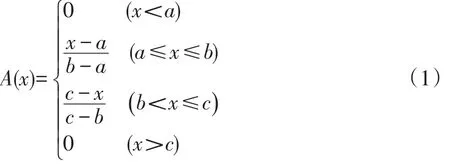
梯形模糊数表示为A=（a，b，c,d），隶属函数为：

式中：a，b，c，d分别为模糊数的上下限。

专家对收球区故障树中底层事件发生的可能性做出主观判断。在确定底事件发生概率时经常使用“德尔菲”方法，即要求多名专家分多轮估计底事件发生概率，这时就要对多个专家估计进行合成，常用的方法是选用模糊集的λ截集和加权平均值的方法组合不同的专家意见。根据模糊集截集的定义，λ截集为[0,1]上的闭区间[8]，λ截集见表2。

根据区间数的运算法则[9]，求专家评估意见的加权平均模糊数的关系函数。

表2 模糊数形式与λ截集

例如，5位专家对站场收球区失效的底层基本事件“存在疲劳裂纹X1”各自进行了一轮估计，结果分别为“小、较小、小、很小、较小”，根据各专家知识层次和实际经验的不同，可认为各专家具有不同的“置信度”。采用参考文献[7]中确定专家权重的方法，根据专家情况，采用强制比较法对其进行赋值，得到各专家权重情况：W1=0.201 3、W2=0.198 2、W3= 0.215 6、W4=0.195 3、W5=0.189 6。根据模糊集截集的定义，“小、较小、小、很小、较小”的λ截集为[0,1]上的闭区间，依次为：A1==[0.1+0.1λ，0.3-0.1λ]、A2==[0.2+0.1λ，0.5-0.1λ]、A3==[0.1+0.1λ，0.3-0.1λ]、A4==[0，0.2-0.1λ]、A5==[0.2+0.1λ，0.5-0.1λ]，其中A1=A3，A2=A5,。实数上的闭区间称为区间数，是一类特殊的模糊数，区间数之间的四则运算法则如下：

设Wλ为专家加权平均估计模糊数，根据区间数的运算法则有：

根据模糊集扩展理论知，Wλ也是模糊集。

令Wλ=[x1,x2]=[0.08047λ+0.11925,-0.1λ+0.35803],则可得到：和，所以平均模糊数的关系函数为：

2.1.3 将模糊数转化为模糊可能性值FPS

采用Lin C.T和Wang M.J.提出的左右模糊数排序法[10]，将模糊数转化为模糊可能性值。此方法定义的最大模糊集和最小模糊集分别是：

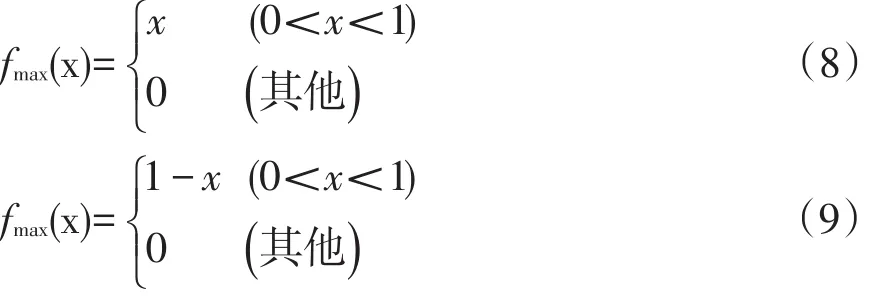
则模糊数W左右模糊的模糊可能性值为：

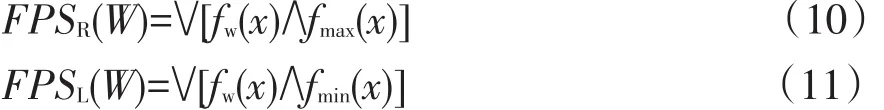
式中：fw(x)为模糊数W所对应的隶属函数；W为对应失效可能性等级的模糊数；“∨”和“∧”分别表示取大和取小。

计算W的模糊可能性值：

2.1.4 将模糊可能性值转化为模糊失效概率FFR

根据参考文献[10]，将模糊可能性值转化为模糊失效概率，转化公式如下：

2.1.5 计算收球区顶事件模糊失效概率

假设各失效风险因素相互独立，利用风险区块失效故障树最小割集的布尔代数方程，可以计算出收球区顶事件模糊失效概率，具体计算见式（14）。

2.2 失效后果分析

失效后果分析采用API 581的计算方法。本文以设备和管道破裂、瞬时泄漏作为失效后果计算的前提条件。

2.2.1 气体泄漏速率计算r

1）当P/P0≥((r+1)/2)r-1时，气体泄漏速率计算公式见式（15）[11]：

2）当P/P0＜((r+1)/2)r-1时，气体泄漏速率计算公式见式（16）：

式中：Q为气体泄漏速率，kg/s；P为容器内介质压力，Pa；P0为大气压力，Pa；r为热容比，取1.33；δg为气体泄漏系数，当裂口形状为圆形时取1.00，三角形时取0.95，长方形时取0.90；A0为裂口面积，m2；ρg为容器内气体密度，kg/m3；M为气体相对分子质量；Z为天然气压缩系数；T为介质温度，K。

2.2.2 失效后果计算

本文采用人员受伤面积作为后果评价指标[12]，借鉴API 581瞬时泄漏不自动点火人员受伤面积CA的计算方法，见式（17）。

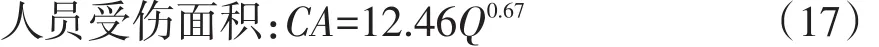
2.3 定量风险计算

收球区的风险值由模糊失效概率与失效后果相乘进行计算见式（18）：

2.4 风险等级划分

借鉴参考文献[13]中对川气东送典型站场失效概率的等级划分，并结合达化输气站收球区的实际情况，对收球区失效概率进行等级划分，从而由公式（18）可计算出收球区失效风险等级划分区间。收球区风险等级划分及其意义见表3。

表3 收球区风险等级划分及其意义

3 实例分析

以达化输气站收球区为例，进行风险区块定量风险评价。目前，该输气站的输送气量为290× 104Nm3/d，进站压力为6.0 MPa，出站压力：去川投燃气为4.2 MPa、去润发门站为4.4 MPa、去CNG加气母站为4.0 MPa，介质温度15℃。

3.1 模糊失效概率计算

1）专家权重的确定。采用参考文献[7]中确定专家权重的方法，根据专家情况，采用强制比较法对其进行赋值，得到各专家权重情况：专家A权重0.201 3，专家B权重0.198 2，专家C权重0.215 6，专家D权重0.195 3，专家E权重0.189 6。

2）计算平均模糊数。5位专家对收球区失效的底层基本事件“存在疲劳裂纹X1”发生的可能性做出主观判断，结果分别为“小、较小、小、很小、较小”。采用λ截集对专家自然语言进行综合处理，“较小、小、很小”的λ截集见表2。根据2.1节，式（7）即为平均模糊数的关系函数。

3）将模糊数转化为模糊可能性值FPS。由式（7）～式（11）可得模糊数W左右模糊的模糊可能性值分别为：FPSR(W)=0.129 7，FPSL(W)=0.765 4。由式（12）得W的模糊可能性值FPS=0.182 2。

4）将模糊可能性值转化为模糊失效率FFR。根据式（13），计算得，K=3.795 6，FFR=1.60×10-4，即“存在疲劳裂纹X1”为1.60×10-4。

同理，可以算出其他底层基本事件的模糊失效概率FFR，见表4。

最后，利用公式（14）便可以算出达化输气站收球区的模糊失效概率为3.55×10-3。

3.2 失效后果计算

在安全措施的保护及站场应急反应下泄漏持续时间通常不超过5 min，因此以泄漏时间5 min来进行收球区失效后果的计算。由于P/P0≥1.85，故利用公式（15）可以算出Q=56.7 kg/s。从而由公式（17）可以算出CA=6 046 m2。

3.3 风险值计算

由表3可知，收球区风险等级划分见表5。

由公式（18）可以算得收球区的风险值R= 3.03。由表5可知，收球区的风险等级为低。评价结果与现场收球区实际风险程度一致。

4 结论

1）采用模糊失效概率来确定输气站场风险因素的失效概率，解决了输气站场因缺乏风险因素的客观失效概率而无法进行定量风险评价的难题。

表4 基本事件模糊失效概率表

表5 收球区风险等级划分

2）通过对达化输气站收球区的风险评价表明，笔者提出的定量风险评价方法具有一定的实际可操作性，同时对输气站场其他功能区块的风险评价也有一定的借鉴意义。

[1]王婷,项小强,戴联双,等.输油气站场HAZOP分析方法及其应用[J].天然气工业,2011,31(10)：97-100.

[2]施林园,郑洁,李晶.四川输气站场风险评价研究[J].天然气工业,2004,24(11)：135-138.

[3]冯文兴,税碧垣,李保吉,等.定量风险评价在成品油管道站场的应用[J].油气储运,2009,28(10)：10-13.

[4]冯文兴,贾光明,项小强,等.原油管道站场的定量风险评价[J].油气储运,2012,31(3)：181-183.

[5]赵新好.输气站场设施风险评价技术研究[D].成都：西南石油大学,2012.

[6]谢云杰,姚安林,钱浩,等.海底管道系统失效可能性评价方法研究[J].中国海上油气,2007,19(2)：134-137.

[7]乐丛欢,丁红岩,董国海,等.基于模糊故障树的海洋立管破坏失效风险分析[J].自然灾害学报,2012,21(2)：173-179.

[8]朱云斌,黄晓明,常青,等.模糊故障树分析方法在机场环境安全中的应用[J].国防科技大学学报,2009,31(6)：126-131.

[9]孙德青.液化石油气球罐的可靠性管理研究[D].成都：西南石油大学,2007.

[10]Lin C.t.,Wang M.J.Hybrid fault tree analysis using fuzzy sets [J].Reliability Engineering and System Safety,1997,58(3)：205-213.

[11]陈国华.风险工程学[M].北京：国防工业出版社,2007.

[12]谷志华,帅健,董绍华.应用API 581对输气站进行定量风险评价[J].天然气工业,2006,26(5)：111-114.

[13]廖柯熹，牛化昶，张学洪，等.川气东送管道典型站场风险量化评价[J].天然气与石油，2012，30（1）：5-9.

In view of the lack of objective failure probability of risk factors in gas transmission stations at present in China,it is proposed to determine the failure probability of risk factors in the gas stations using fuzzy failure probability.The method is based on expert judgment,and uses fuzzy set theory to transform the expert judgment result into fuzzy failure probability.Taking the injured area of personnel as the evaluation index of the failure consequence,the risk value is calculated and the risk grade division method is put forward.Finally, the risk of the receiving ball area of Dahua gas station is evaluated,and the evaluation result is consistent with the actual risk level.

natural gas station；risk block；quantitative risk assessment；fuzzy failure probability；failure consequence

王梅

2017-03-18

李平（1986-），女，硕士，主要从事油气长输管道风险评价与完整性管理工作。