基于高雷诺数的并联双圆柱绕流研究
2017-08-01庞建华
庞建华,宗 智,周 力
(大连理工大学 工业装备与结构分析国家重点实验室,辽宁 大连 116024)
基于高雷诺数的并联双圆柱绕流研究
庞建华,宗 智,周 力
(大连理工大学 工业装备与结构分析国家重点实验室,辽宁 大连 116024)
文章采用基于边界瞬时涡量守候的拉格朗日方法(IVCBC),结合并列双圆柱的特点,建立了双圆柱绕流数值计算模型。对高雷诺数下Re=6×104,间隙率为T/D=1.1~7的并联圆柱双圆柱二维绕流特性进行了研究。提出了双圆柱间隙中点的速度区别宽窄尾流的新方法。分别讨论了流体力系数随间距增加的特点,脉动流体力的特点,尾流特征以及斯托哈尔数特征。研究发现:区别宽窄尾流的新方法是可靠的;在双圆柱尾流附近有五种尾流模型存在;同时发现了在宽窄尾流的频率,存在一个中间频率。
(IVCBC)涡方法;并联双圆柱;宽窄尾流;高雷诺数;中间频率
0 引 言
并联多圆柱绕流特征与单圆柱绕流有本质的区别,探索其特点对实际的工程设计和制造有积极的指导作用,在低雷诺数下已经被广泛地研究,在海洋工程中,实际装备大多处于高雷诺数工况下,然而基于高雷诺数的双圆柱绕流研究甚少。
本文基于高雷诺数Re=6×104工况下采用改进的涡片法对双圆柱之间不同的间隙的流体特征进行了研究。首先基于涡方法,建立双圆柱绕流数值模型。对间隙率为T/D=1.1~7的范围进行研究,建立了全新的区别小间距的宽尾流和窄尾流新的方法,分析了两个圆柱的升力,阻力,脉动动力,同时对两尾流的泄涡频率进行了分析,最后区别了尾流的模型。研究发现:两圆柱间隙中心点的速度方向与间隙流的偏转方向同步;基于宽窄尾流的频率之间存在一中间频率;升力和阻力系数随着间距的增大先迅速减小,T/D=0.5附近再迅速增大,在T/D=1.5接近最大值,最后缓慢下降达到一个圆柱的阻力值;同时在尾流中发现了5种尾流模式。
1 并联双圆柱的计算模型
采用本文改进基于流函数—涡量方程的涡方法(IVCBC)[1],其边界条件的满足是以结构边界为流线这一事实建立方程。由于涡元的对流和扩散,新的流场不再满足结构边界为流线这一事实,为此结合边界层理论,选择在边界层分布新的涡元,以满足结构边界为流线,这样反复更替,建立涡方法的时域方程,从而达到对结构物绕流的仿真。
该涡方法的并联双圆柱绕流的数值计算如图1所示,采用M数值点代表圆柱表面,这些点被称为控制点。在距离数值表面距离中c等于2)处用另外M个涡元代表剪切层,通过流函数的叠加性,获得数值表面的流函数,根据二维结构面为一流函数这事实,建立新生涡产生的方程,最终实现涡不断的对流和扩散。其数值方程建立如下。
涡量—流函数方法中,流函数的形式为

根据流函数的可叠加性,第k个控制点处的流函数为
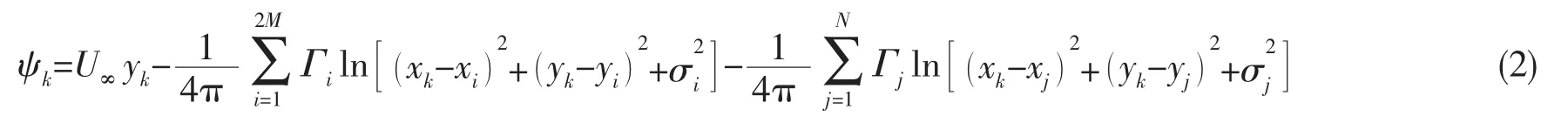
式中:2M和N表示新生成的涡元和尾流场中涡元的总数目。 (xi, yi)、 (xj, yj)和 (xk,yk)分别表示新生涡元、尾流涡元以及控制点的位置。
对于圆柱的光滑表面,表面是流线型的。流函数的值等于流线上任何位置的一个常量。我们能够得到两个相邻控制点的流函数方程
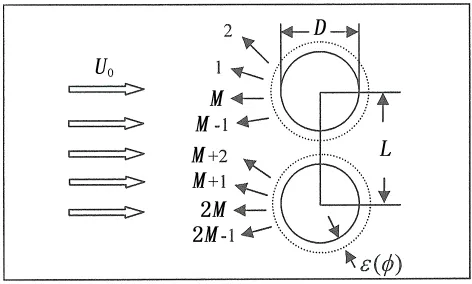
图1 涡产生模型Fig.1 The model of vortex generation

由于2M控制点位于两圆柱表面上,所以有2M个方程涉及2M个未知变量(新涡的强度),而且第(2M+1)个方程表明了涡量守恒。根据最小二乘法可以得到一个线性代数方程组


式中:Γi表示涡元的强度,通过高斯消元法获得方程的解。
每个圆柱上的升力和阻力计算如下:

涡的对流扩散,涡的融合和消去同第一章和第二章描述的一致。在接下来的两并列圆柱绕流的模拟中,雷诺数为6×104时采用涡数为64和时间步长为0.1。
2 宽尾流和窄尾流的区别方法
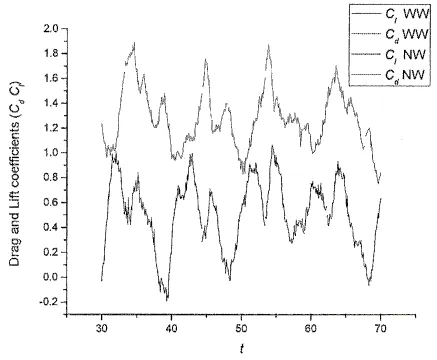
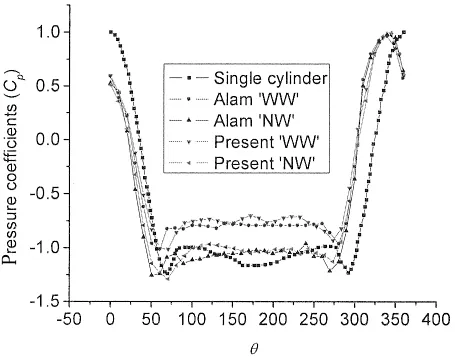
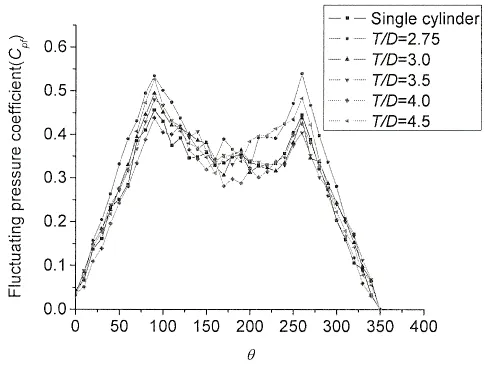
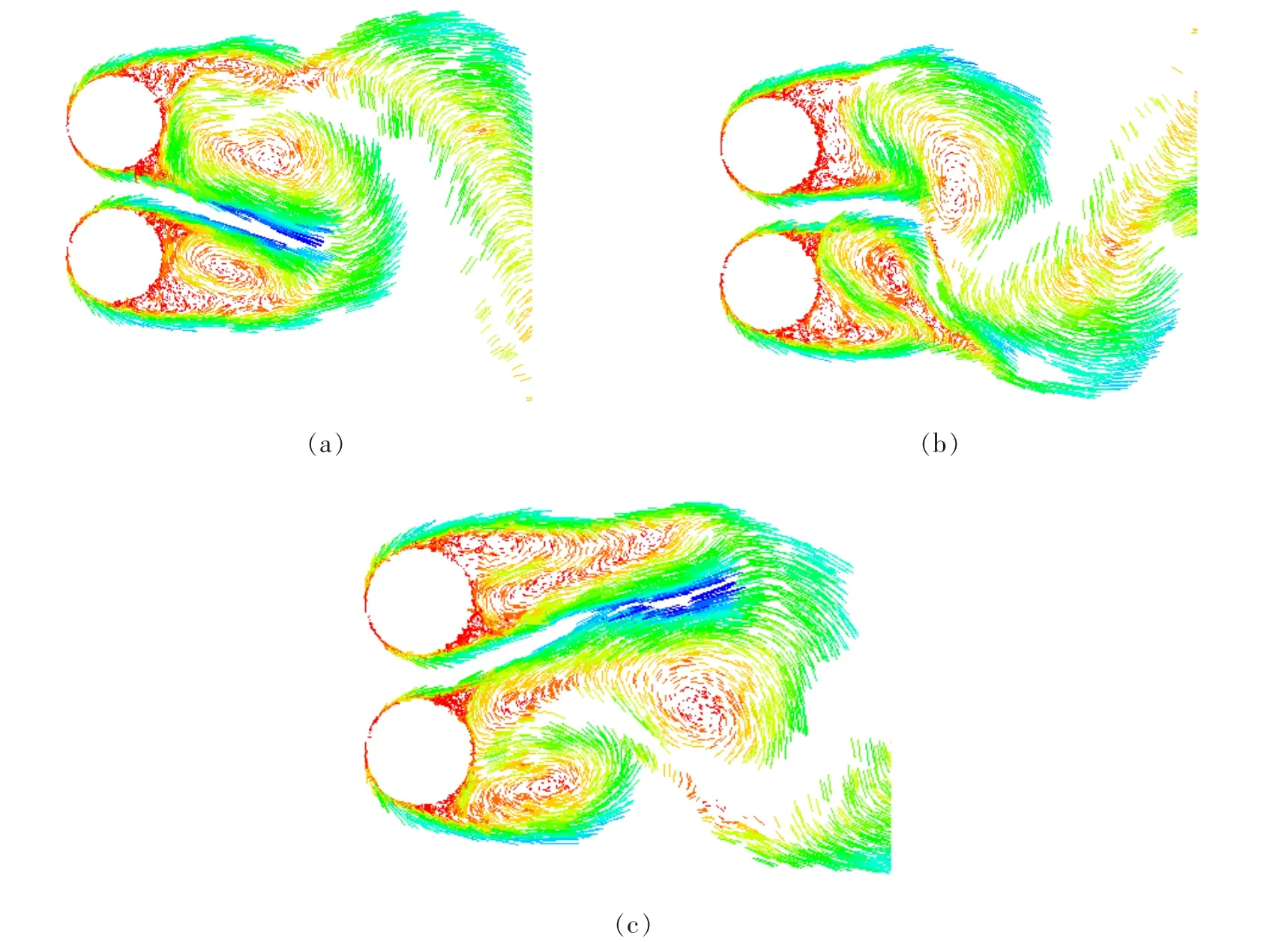
当并联圆柱之间的间距较小大约在1 这种特殊的涡量场的分布决定间隙流的偏转方向,同时涡量场决定速度场,速度场确定流体的运动方向。由此可见,间隙流的偏转方向与速度场分布有一定联系。经研究发现,两圆柱中心的连线上一点的速度方法与间隙流偏转同步。通过比较和分析,如图2所示,点A(0.25D,0) (连接两圆柱尾部边缘(X/D=0.5)的垂线设为BC。从上圆柱的中心画到另一圆柱中心的直线被标记为EF。连接两条直线BC和EF的中点,然后连线的中点就是特殊点A。)的诱导速度方向与间隙流的偏转方向同步。当A点沿y轴方向的诱导速度为零时,间隙流从一个圆柱向另一圆柱偏转。之后,当间隙流转向上部圆柱时,A点沿y轴方向的诱导速度是正值,而当间隙流偏向低位的圆柱时,沿y轴方向的诱导速度是负值。 为了验证A点的诱导速度方向转变与间隙流的偏转方向的同步性,本文选择在Re=6.0×104的流体工况下,涡方法的参数为Δt=0.1,Nv=64圆柱之间的间隙为T/D=1.2时进行计算。图3为A点在y轴方向的速度时程图,通过对时程图的低通滤波消除高频噪音得到光滑的时程图如图4所示。图5展示了间隙流发生偏转时刻的瞬时涡量轮廓图。从这几个图中清晰地展示了间隙流的偏转与A点产生的y轴方向上的诱导速度正负转变同步,又知间隙流的偏转的本质来自宽尾流和窄尾流诱导,从而间隙流的速度正负的转变可以正确地区别宽窄尾流。同时也能区别出圆柱绕流中上圆柱与下圆柱是宽尾流和窄尾流的所受的流体力如图6。这样可对研究这一特殊的流场提供一种全新的区别宽尾流和窄尾流的方法。本文在接下来对并联双圆柱的研究中就采用这一方法区别宽窄尾流。 图2 区别宽尾流和窄尾流的特殊点Fig.2 The position of a specific point A(0.25D,0)disturbing NW and WW 图3 点A(0.25D,0)的y轴方向的速度时程图Fig.3 Distributions of velocity time history at point A(0.25D,0) 图4 低通滤波之后的速度时程图Fig.4 Distributions of velocity time history after low-pass filtering 图5 瞬时涡量轮廓图Fig.5 The instantaneous vorticity contours 本节基于高雷诺数Re=6×104工况下采用改进的涡片法[2]对双圆柱之间不同的间隙的流体特征进行了研究。将间隙率(1.1≤T/D≤7)分为(1.1≤T/D≤1.2),(1.2≤T/D≤2.6),(2.6≤T/D≤7)三个范围,分析在这三个范围内,两个圆柱的升力、阻力、脉动动力和两尾流的泄涡频率和尾流模型。 3.1 尾流模式 图6 上圆柱的宽窄尾流的升力和阻力分布Fig.6 Distributions of lift and drag coefficients of NW and WW for upper circular cylinder 数据结果表明,两并列圆柱附近存在五种主要流动模式:在间距比为(1.1≤T/D≤1.2)范围内,并联双圆柱尾流模型与单圆柱绕流的模型相同;在不对称形式(1.2≤T/D≤2.6)范围内存在不对称偏转流模式;在间隙率为(2.6<T/D<7)范围内存在对称的同相流动模式、反相流动模式以及混合流模式(即反相和同相同时存在)。 在小间距比(1.1≤T/D≤1.2)范围内,两个圆柱绕流的尾流模型类似于单个圆柱,如图7所示。在尾流中形成了较大的卡门涡街。这是因为当两个圆柱的间距很小,两圆柱内侧剪切层的相互作用使得两柱体之间的涡量强度小,导致外剪切层的环流强度比内剪切层的要大很多,从而流动模式主要由外剪切层的相互作用决定。这一机制与单圆柱的相似,这也与Alam等人[2]的实验结果一致。 图7 瞬时涡量轮廓(T/D=1.1)Fig.7 Instantaneous vorticity contours at T/D=1.1 在非对称范围(1.2<T/D<2.6)内,圆柱后面的尾流模式表现不稳定和不对称如图8所示。在这种流动形式下,由于两圆柱表面随机地使旋涡脱落和尾流之间的相互作用,两圆柱之间的间隙流发生偏转,在这个范围内,出现特殊的宽尾流和窄尾流现象,间隙流的偏转表现为随机性。 图8 瞬时涡量轮廓图(T/D=1.5)Fig.8 Instantaneous vorticity contours at T/D=1.5 间距比增加到(2.6<T/D<6),不对称的尾流特点消失。两圆柱的尾流出现对称性的冯卡门涡激,其流体模式表现为三种同步特点,即同相流同步模式、反相同步模式和混合同步模式。从模拟中发现,反相同步模式是主要的,这个结果与Alam等人[2]的是相似的。图9展示了三种典型的反向模型其间距比分别为T/D=3.2,3.7和4.2,相应的升力和阻力系数的时程图如图10所示。从时程曲线可观察到反相同步模式。在图9(a)中可以清晰地观察到这种模式在双圆柱的下游持续了很长时间,这与Zhou等人[3]的描述完全吻合。然而,在图9(b)和图9(c)中,前面的尾流对迅速地融合在一起,这体现了并联双圆柱尾流涡街之间复杂的相互作用。图11展示间距比为T/D=3.95和4.95同相同步模式的两个例子,可以看出泄涡方式是同步,但不同相位的。图12清晰地看出两个双圆柱升力系数的同相位同步的特征。图13和图14展示了尾流中既有同相位也有反相位的尾流模式。 图9 瞬时涡量轮廓图(T/D=3.2,3.7,4.2)Fig.9 Instantaneous vorticity contours at T/D=3.2,3.7,4.2,respectively 图10 上下圆柱的升力分布(T/D=3.2,3.7,4.2)Fig.10 Distributions of Clfor upper and lower circular cylinder at T/D=3.2,3.7,4.2 图11 上下圆柱的升力分布(T/D=3.95,4.95)Fig.11 Instantaneous vorticity contours at T/D=3.95,4.95 图12 上下圆柱的升力分布(T/D=3.95,4.95)Fig.12 Distributions of Clfor upper and lower circular cylinder at T/D=3.95,4.95 图13 上下圆柱的升力分布(T/D=4.45)Fig.13 Instantaneous vorticity contours at T/D=4.45 图14 上下圆柱的升力分布(T/D=4.45)Fig.14 Distributions of Clfor upper and lower circular cylinder at T/D=4.45 3.2 平均表面压力系数 图15显示间距比为T/D=1.5的上层圆柱表面的平均压力系数 Cp( )。为了作比较,由Alam等人[2]测量的两并列圆柱的实验结果也被包括在图中。可以看出,在上层圆柱上模拟的驻点大约是340°,而不是0°,与Alam等人[2]的实验结果一致。从涡的运动过程观察到了有趣的现象,对WW(宽尾流)和NW(窄尾流),两个驻点的位置几乎保持不变,这阐明偏流对WW和NW的停滞点的位置影响很小。此外,θ<55°与θ>305°时NW和WW的表面压力几乎一致,而且在其他角度WW的压力值比NW的大得多。这导致了WW背面较大,从而表现出阻力较小,这与Afgan等人[4](2011)和Alam等人[2-5]的结果相吻合。 图16分别比较了间距比为T/D=1.1,1.25,1.5,2.0的上层圆柱的平均压力系数。从图中,我们观察间距比为T/D=1.1的窄尾流的表面压力分布,可以看出,表面上的涡在大于75°分离柱体表面,在115°~250°范围内表面压力值明显的低于宽尾流的表面压力值。形成在圆柱后侧相对较大的负压区,从而导致圆柱的窄尾流的阻力大于宽尾流的阻力。观察其他的窄尾流,流体分离后,压力变化趋于平缓,从表面压力积分可得压力这一个观点,可以得出T/D=1.1时的窄尾流的阻力系数比其他间距比的压力系数都大。从图中还能观察到间距比为T/D=1.1,1.25,1.5,2.0时,驻点的位置分别是350°、250°、150°和100°,这说明随着间隙比的增加,间隙流的偏转程度逐渐减弱。这与Bearman等人[6]的研究的结果相符。 图15 上层圆柱的表面压力系数分布(T/D=1.5)Fig.15 Distributions of pressure coefficient along the surface of the upper cylinder(T/D=1.5) 图16上圆柱的表面压力系数分布(T/D=1.1;1.25;1.5;2.0)Fig.16 Comparison of the pressure coefficients along the surface of upper cylinder at T/D=1.1;1.25; 1.5;2.0,respectively. 图17 分别显示在T/D=2.75,3.0,3.5,4.0和4.5的平均表面压力系数。从图中我们可以观察到,压力系数的轮廓线几乎是对称的,而且驻点位于θ=0°处。这表明,T/D>2.75时双圆柱的非对称作用逐渐消失,表现场处明显的对称性,这与3.1节中尾流特点是一致的。 3.3 脉动表面压力系数 图18分别描述了在 T/D=1.1,1.25,1.5和2.0时,脉动表面压力系数 Cpf( )的分布。可以看出Cpf在T/D=1.1时是相对较高。这表明圆柱表面的压力波动范围较大,也说明,尾流中涡量分布变化较大,导致了柱体表面的速度变化较大,从而压力的脉动性较大。这一结果符合由Zdravcovich等人[7]测量的实验观察的结果。同时可以观察到WW的Cpf分布略高于NW,这表明NW在整个区域内的剪切层产生的涡量变化不大。当涡从柱体表面分裂的短暂过程中,这个区域速度变化较大,从而导致表面压力较大的波动而产生了一个峰值,从图中可以看出它非常接近分离点,这一点与Alam等人[2]观察的结果一致。 图19显示在T/D=2.75~4.5时的脉动压力系数分布。我们可以观察到随着T/D增加Cpf逐渐减少,而且在T/D=4.0和4.5时Cpf与单圆柱的值接近,这说明随着T/D增加,尾流的相互作用几乎消失,尾流的模式接近单元柱的特征。这结果与Alam等人[2]和Guo[8](2004)在先前进行的实验完美相符。 图17 上圆柱的表面压力系数分布(T/D=2.75,3.0,3.5,4.0,4.5)Fig.17 Distributions of pressure coefficients along the surface of upper cylinder at T/D=2.75,3.0,3.5,4.0 and 4.5, respectively 图18 脉动压力系数分布(T/D=1.1,1.25,1.5,2.0)Fig.18 Distributions offluctuating pressure coefficient Cpf( )(T/D=1.1,1.25,1.5,2.0) 图19 脉动压力系数分布(T/D=2.75,3.0,3.5,4.0,4.5)Fig.19 Distributions of fluctuating pressure coefficient Cpf( )(T/D=2.75,3.0,3.5,4.0,4.5) 3.4 升力和阻力系数 图20描绘了间距比为T/D=1~7时的平均阻力系数 Cd( )分布,其中间距比为T/D=1~2.6分别列出NW和WW的阻力系数 Cd( )。为了比较,Zdravkovich等人[7],Hori等人[9](1959)和Alam等人[2]得到的实验结果也包括在图中。从图中可以看到由上述方法计算的NW的Cd在T/D=1.1时是最大的。在1.2<T/ D≤2.6时,NW的Cd比WW的Cd略大,这是由于尾流窄,其速度快,在圆柱后形成的负压大(Alam等人[2])。当间距比非常小时,由于两圆柱内侧剪切层非常接近,间隙流的速度减小,尾流的影响主要来自两圆柱外侧的剪切层作用,这样在双圆柱的后侧形成较大的负压,此时压力系数较大。随着间距的增大,双圆柱内侧的剪切层的影响迅速下降,间隙流速度迅速增大,发生较大的偏转,导致圆柱后侧的负压增大,从而压力迅速减小。当间隙比更高时,间隙流的偏转变小,对柱体后侧的影响较小,涡环流的的速度逐渐增大,导致圆柱后侧的负压增大,从而压力柱体的阻力也逐渐增加。这与前面的表面压力分布是一致的。随着间距比继续增加,环流速度趋于稳定,这样圆柱后侧的表面压力趋于平稳,阻力也趋于平稳。因此在2.6<T/D≤4.5时,间隙流略微有偏移,而且两圆柱的绕流的特点相似。当T/D>4.5时,尾流的相互作用几乎消失,Cd与单圆柱的值接近。 图20 上圆柱的阻力系数分布Fig.20 Distributions ofdrag coefficientfor upper cylinder with respect to T/D 图21 上圆柱的升力系数分布Fig.21 Distributions oflift coefficient for upper cylinder with respect to T/D 图21展示了上部圆柱的升力系数随间距比变化的分布图。图中看出目前计算的升力系数与Alam等人[2],Hori等人[9]和Jendrzejczyk等人[10]测量的实验值趋势几乎一致。图中可看出升力系数在间距比较小时,升力系数较大,这是由于,间隙比很小时,在两个圆柱的中间间隙流流动被阻挡,使得上圆柱的右下侧的作用力较大,从而产生较大的升力。随着间距比增加,间隙流快速通过两圆柱间隙,使得圆柱右下侧的流体不再受阻,同时由于两圆柱上下剪切层的流体产生较大的回流区,使得间隙流的速度增加,这样,间隙表面的压力减小,从而导致升力迅速减小,当间隙比继续增加时,圆柱右下侧产生的表面压力逐渐减弱,双圆柱之间的相互作用减少,导致升力趋于柱的间隙表面的边界层影响区域平稳,升力逐渐和单个圆柱的升力一致。 图22 脉动阻力系数随间隙比的分布Fig.22 Distribution of the fluctuating drag coefficient with respect to T/D 图23 脉动升力系数随间隙比的分布Fig.23 Distributions of the fluctuating lift coefficient with respect to T/D 3.5 脉动表面压力系数 脉动阻力系数 Cdf( )和脉动升力系数 Clf( )的分布分别显示在图22和图23中。由Alam等人[2]的实验结果也列在其中。可以看出在小间距比(1.1≤T/D≤1.2)范围内,Clf和Cdf的值更高,在不对称体制下(1.2<T/D≤2.6),值是相对较小,在对称体制下(2.6<T/D≤7),值与单圆柱的数值几乎完全相同。从图中看出在间距比为(1.1≤T/D≤2.6)范围内,升力和阻力的脉动值由强到弱再由弱到强。这说明,在间距比极小时,圆柱上下表面的压力值振动较大,这是因为间隙流的流动被阻挡,尾流主要是由两侧边界层相互作用形成较大的漩涡,漩涡由于间隙流的影响,导致对圆柱边界层的影响较大,当间隙比增大,间隙流的阻碍降低,引起表面压力分布的变化逐渐趋于平稳,这样导致升力和阻力的脉动系数趋于平稳。随着间隙比的逐渐增加,间隙流发生偏转和宽窄尾流的作用,使得圆柱表面的表面压力变化较大,导致了升力和阻力脉动性较大。说明流体对柱体的影响变化较大。随着间距比继续增大,不对称的流逐渐变为对称流,圆柱之间的影响逐渐减弱,圆柱表面压力变化区域平稳。 3.6Strouhal数和中间频率 图24间隙比不同的尾流频率Fig.24 Distributions of Strouhal numbers for T/D 图24 展示了圆柱的升力系数时程图的频率随间距比的分布。在T/D≤2.6时,WW和NW的Strouhal数的分布与由Alam等人[2]先前测量的结果趋势吻合。当T/D>2.6时,两圆柱的Strouhal数接近单圆柱的值,这值为0.196。此外,我们发现在NW和WW的相应数值之间的一组Strouhal数,它们与单圆柱的值接近。这种现象也可以在图25中的可视化图片中观察到,在图25(a)-(c)图片中看到间隙流从一个圆柱偏向另一个圆柱。在这个两个圆柱发生偏转的中间,间隙流的偏移不发生时,存在一种介于宽尾流和窄尾流频率之间的中间频率如图25所示。从图26升力系数的FFT分析中,我们可以观察到三个峰值。第二个峰值位于频率为0.2,该值非常接近单圆柱的Strouhal数。 图25 宽窄尾流模式Fig.25 Visualized flow pattern for NW and WW(T/D=1.5) 本文基于第三种改进的涡方法,针对高雷诺数Re =6.0×104,建立了基于纯拉格朗日涡方法的两个并列圆柱绕流的二维计算模型。针对特殊尾流的小间距比下,存在宽尾流和窄尾流,本文给出一种新型区别宽窄尾流的方案,通过判断间隙流中一个特殊点的速度方向,精确判断窄尾流(NW)和宽尾流(WW)。在模拟过程中,研究了三种主要尾流区域中的五种模式:在小间距比区域(1.1≤T/D≤1.2)内,双圆柱的绕流特征与单圆柱的绕流特征相似;在不对称区域(1.2<T/D≤2.6)内,间隙流随机地从一个圆柱偏向另一个圆柱;在对称体制下(2.6<T/D≤7),流场恢复了它的对称性而且产生了三种主要流动模式,即同相同步流动模式、反相同步流动模式以及混合流动模式。反相同步流动模式在多种模式中占主导优势。同时发现在特定间距比下同相同步尾流模式可以持续很长时间。通过分析表面压力、脉动表面压力、阻力和升力系数、脉动阻力和升力系数的水动力值被计算和分析,我们发现在(1.1≤T/D≤2.6)时的Strouhal数(St),存在一个介于窄尾流(NW)和宽尾流(WW)频率之间的中间频,而且与单圆柱的频率接近。 图26 升力系数的频谱分析Fig.26 FFT analysis ofthe liftcoefficientat T/D=1.5 [1]Pang Jianhua,Zong Zhi.Improving discrete vortex method for investigation of the fluctuating forces acting on a circular cylinder at subcritical Reynolds number[C]//Proceedings of 3rd International CFD Conference.Dalian,China,2014. [2]Alam M M,Moriya M,Sakamoto H.Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon[J].J Fluid Struct,2003,18(3):325-346. [3]Zhou Y,Zhang H J,Yiu M W.The turbulent wake of two side-by-side circular cylinders[J].J Fluid Mech,2002,458:303-332. [4]Afgan I,Kahil Y,Benhamadouche S,Sagaut P.Large eddy simulation of the flow around single and two side-by-side cylinders at subcritical Reynolds numbers[J].Phys.Fluids,2011,23(7):075-101. [5]Alam M M,Zhou Y.Flow around two side-by-side closely spaced circular cylinders[J].J Fluid Struct,2007,23(5):799-805. [6]Bearman P W,Wadcock A J.The interaction between a pair of circular cylinders normal to a stream[J].J Fluid Mech,1973,61(3):499-511. [7]Zdravkovich M M,Pridden D L.Interference between two circular cylinders;series of unexpected discontinuities[J].J Wind Eng.Ind.Aerod,1977,2(3):255-270. [8]Guo M M.Synchronous measurement ofsurface pressure distribution and fluctuating aerodynamic forces on two circular cylinders[M].Shanghai:Fudan University Press,2004. [9]Hori E.Experiments on flow around a pair of parallel circular cylinders[C].In:Proceedings of the 9th Japan National Congress for Applied Mechanics,1959:231-234. [10]Jendrzejczyk J A,Chen S S.Fluid forces acting on circular cylinders in liquid cross flow[R].Am.Soc.Mech.Eng.,Pressure Vessels Piping Div.,(Tech.Rep.)PVP;(United States)63.(CONF-820601-),1982. Numerical investigation of the flow around two side-by-side circular cylinders based on high Reynolds number PANG Jian-hua,ZONG Zhi,ZHOU Li A novel pure-Lagrangian vortex method based on instantaneous vorticity conserved boundary conditions(IVCBC)was applied to investigate the hydrodynamic coefficients and patterns of two-dimensionalflow around two circular cylinders in side-by-side arrangements with pitch ratios T/D=1.1~7at a high Reynolds number Re=6×104.The benchmark case of viscous flow around a circular cylinder was first carried out to validate the novel vortex method.Then simulations of the flow around two side by side circular cylinders were performed.A new scheme was proposed to distinguish the wide wake(WW)and narrow wake (NW)by judging the velocity direction of a specific point in the gap flow.The hydrodynamic coefficients and Strouhal numbers were thoroughly studied as a function of the pitch ratios.A total of five kinds of flow patterns were identified.During the investigation of biased flow,an intermediate frequency between frequencies of NW and WW was found and approached to that of a single cylinder.The results show good agreement with the previously published experimental and numerical data. IVCBC vortex method;two side-by-side circular cylinders;NW and WW; high Reynolds number;hydrodynamic coefficients;intermediate frequency O35 A 10.3969/j.issn.1007-7294.2017.07.001 1007-7294(2017)07-0791-13 2016-12-21 973资助项目(2013CB036101);国家自然科学基金重点资助项目(51639003);国家自然科学基金项目(51679037,51279030);高技术船舶专项资助 庞建华(1985-),男,博士研究生,E-mail:njpjh@sina.com; 宗 智(1964-),男,教授,博士生导师。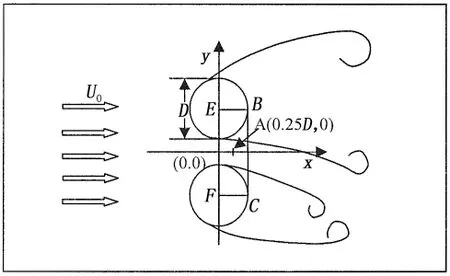




3 并联双圆柱的绕流特征

















4 结 论

(State Key Laboratory of Structural Analysis for Industrial Equipment,Schoolof Naval Architecture, Dalian University of Technology,Dalian 116024,China)
