石墨烯吸附Li团簇的第一性原理计算∗

杨光敏 梁志聪 黄海华

1)(长春师范大学物理学院,长春 130032)

2)(吉林大学材料科学与工程学院,长春 130012)

石墨烯吸附Li团簇的第一性原理计算∗

杨光敏1)2)†梁志聪2)黄海华2)

1)(长春师范大学物理学院,长春 130032)

2)(吉林大学材料科学与工程学院,长春 130012)

(2016年9月17日收到;2016年12月4日收到修改稿)

构建了单层六方石墨烯超晶胞结构,以吸附不同尺寸的Li团簇,Li:C摩尔比例皆为1:6.采用基于密度泛函理论的第一性原理,计算了其态密度、差分电荷密度、能带,分析了Li团簇与石墨烯吸附前后的电荷分布情况及Li-C成键类型,二者之间的电荷分布决定了两者的相互作用.使用热力学的方法及成核机制进行分析,得出成核的可能性与团簇尺寸的关系,研究了一定浓度下的锂在石墨烯上的成核问题.相应的计算结果有助于理论上深入理解锂电池储能机理.

石墨烯,Li团簇,电子结构,第一性原理

1 引 言

逐年递增的能源需求量、日趋严峻的环境现状、对于高效可再生清洁能源的迫切需求是目前人类社会面临的三大问题.新型环保节能设备,如锂离子电池等在这一时代背景下应运而生,并在当今社会逐渐地占有一席之地.新型锂离子电池具有体积小、循环寿命长、能量密度高等优点[1−3].由于锂离子电池的性能和应用与电极材料及储能机理密切相关,其技术发展核心之一是电极材料的设计.通常锂电池正极材料为钴酸锂,负极材料以石墨为主,但是石墨比容量低,无法满足当今市场要求.作为锂离子电池的主要组成部分——负极材料,其性能直接影响锂离子电池的综合性能.早期的负极材料直接使用锂单质,但具有安全隐患和循环性差的缺点.而锂合金则比电容较高,但放电能力会随着时间逐步降低,充放电过程中,锡基材料体积变化很大,而含锂过渡金属氮化物容量衰减很明显.石墨烯自被发现以来,因良好的物理化学性能,在锂离子电池方面受到了广泛关注[4−6].国内外研究表明,作为锂电池的负极材料——石墨烯,皆为提高其比电容而开展的研究,即石墨烯上吸附锂原子的数量,进一步研究锂在石墨烯上的微观机制,以求在根本上提升比电容.石墨烯纳米片、无序石墨烯纳米片、氧化石墨烯纳米棒在实验上均证实具有良好的循环稳定性和高的可逆电容[7,8].实验结果表明增加锂和碳之比大约1/2是有可能的[9−11].最新拉曼光谱显示,少层锂嵌入单层和少层石墨烯有类似石墨的行为,目前,很多国内外专家从事Li-C相互作用机理方面的计算研究[12−14].Khantha等[15]计算表明,锂可以吸附在石墨烯表面,吸附能在0.943—1.598 eV之间.Chan等[16]表明Li在石墨烯不同的吸附位置具有不同的吸附能,其中碳环中心位置最稳定.最近,Yang[17]计算表明Li2C2拥有1.40 eV的键能,Li—C键被认为离子键性质[18,19],可以使锂更容易扩散.在低浓度下,由于库仑力作用,Li在石墨烯上扩散,随着Li浓度升高,发现石墨烯上可形成小型Li团簇,Li团簇的形成会引起电极材料的结构稳定性问题,形成潜在的锂枝晶[20−22].为了提高储能密度,需要尽可能地增加Li吸附的浓度,但吸附锂浓度是有限的,过高锂浓度会带来循环的稳定性问题.基于高浓度Li掺杂下Li-C的相互作用机制,吸附稳定性问题及电荷的定量转移情况值得研究.

本文基于密度泛函理论的第一性原理,研究了石墨烯上Li团簇的吸附行为,及Li在石墨烯上的电学性质及成键类型,定量计算了Li团簇向石墨烯转移的电荷.并对石墨烯上Li团簇的成核机制进行了分析,使用热力学方法及成核机制来研究了成核的可能性与团簇尺寸的关系,并讨论了Li在石墨烯上的成核行为与温度的关系.

2 理论计算

本文的计算采用基于密度泛函理论(DFT)的VASP软件包[23],采用缀加投影波(PAW)方法[24],使用广义梯度近似(GGA)-Perdew-Burke-Ernserhof(PBE)[25]作为交换关联函数.经过对Li-Graphene体系的测试,平面波截止能为550 eV时达到计算精度,在布里渊区积分计算时采用了VASP软件推荐的原点在Γ点的Monkhorst-Pack型网格,总能量收敛在1 meV/atom.由于游离的锂原子具有磁矩,计算参数中加入自旋,ISPIN=2.对于石墨烯的原胞,有两个碳原子被放置在二维蜂窝状的六方晶胞中.优化石墨烯结构得出其晶格常数为2.464 Å[26],与实验2.46 Å相差不大.基于这样的原胞,我们分别建立了的六方结构的晶胞模型,以吸附锂团簇.其相应的超胞的K点网格取22×22,20×12,12×12,10×12,12×8,14×12.此时Li原子个数在各原胞中为1,2,3,4,5,6,故其摩尔比例均为Li:C=1:6.对于含有Li的构型体系,ISMEAR=0.为了避免石墨烯层间的干扰,相邻两层石墨烯之间的距离设为18 Å.我们计算了其态密度、能带结构、电荷密度分布情况.

3 结果与讨论

3.1 石墨烯吸附锂团簇的电学性质

图1(a)和图1(b)分别为优化后的石墨烯吸附Li团簇的超晶胞结构模型及差分电荷密度图,图1(c)为孤立Li团簇的电荷密度分布图.选取锂原子数n=2,3,4,且保持锂原子与石墨烯的比值为1:6,选取最稳定构型的吸附方式.

图1 (网刊彩色)(a),(b)分别为Li2C12,Li3C18和Li4C24的超晶胞结构及对应的差分电荷密度图,红色和绿色分别代表电荷的得失;(c)为孤立Li团簇的电荷密度分布图Fig.1. (color online)Schematic representation of(a)Li2C12,Li3C18and Li4C24,(b)the corresponding to calculated charge density difference in xyplane for the region,the red and green colors represent charge accumulation and depletion,respectively;(c)the charge density distribution of isolated cluster.

图2为石墨烯(C12,C18,C24),Li团簇(Li2,Li3,Li4),及石墨烯吸附Li团簇后(Li2C12,Li3C18,Li4C24)的态密度图.如图2(a)所示,石墨烯是零帶隙材料,具有半金属性质,态密度图形的趋势随晶胞中的原子数成比例增长,趋势一致.图2(b)中Li2C12,Li3C18,Li4C24的态密度(DOS)图所对应的体系中费米能级都向右移.对比分析图C12与Li2C12这一组,Li2C12费米能级左侧有突起峰,这主要是Li原子的贡献.将Li原子看成掺杂,Li原子的一部分价电子运动到石墨烯的体相空间中,所以电子的运动空间就是石墨烯的体相空间.Li原子吸附,完全是由于碳的电负性比Li大,将其一部分电子吸附到了导带上,吸附前后体积不变,粒子数密度变大,费米能级增加,固向右移动[16].为了对比石墨烯吸附Li团簇前后的态密度的变化,我们还计算了孤立Li团簇的DOS图,如图2(c),表明在费米面附近具有较高的电子态,呈现金属特性.

图3(a)—图3(d)分别为LiC6,Li3C18,Li4C24,Li5C30的DOS图和分波态密度(PDOS)图,及孤立Li原子的DOS图.从图3(a)可以看出,Li的PDOS与孤立的Li原子的DOS图相比,本该尖锐的2s峰,却平坦了很多,这个平坦的宽度主要受石墨烯的影响,LiC6中Li原子的大部分电荷转移到石墨烯中.若将电子转移分成两部分,一部分是有关石墨烯,一部分是有关Li原子/团簇.石墨烯实空间中的电子可分为三部分,一部分是石墨烯价带中的电子,一部分为石墨烯中电子因费米能级的移动而迁移到石墨烯价带中的电子,一部分为迁移到石墨烯导带的Li原子/团簇的电子.而有关Li原子/团簇的有两部分,为Li原子/团簇中未被石墨烯吸引而剩余的电子,仍处于导带中,另一部分为从石墨烯中吸引而得到的电子,但是由于锂相对石墨烯类似掺杂,且二者电负性差别很大,Li从石墨烯吸收的电子远小于向石墨烯失去的电子.从宏观键的角度来说,锂与石墨烯之间有共价键的成分和离子键的成分,但以离子键为主.电子的转移与费米分布有关,石墨烯能态密度的变化,归根结底是锂原子的周期势场,微扰石墨烯的周期势场.石墨烯与Li团簇吸附后,Li团簇中的大部分电子转移到石墨烯中,其他三组图3(b)—图3(d),与LiC6相近,不再赘述.为了证实以上对电子结构的分析,我们计算了差分电荷密度,以观察电荷在实空间中的分布情况,如图1(b).差分电荷密度即体系成键后的电荷密度与其对应点的原子的电荷密度之差,通过公式计算可得,∆CH(r)=CHLi-g(r)−CHLi(r)−CHg(r),CHLi-g(r),CHLi(r)和CHg(r)分别代表石墨烯吸附Li团簇,孤立Li团簇和纯石墨烯的电荷密度分布[27],红色和绿色分别代表得失电子,差分电荷密度可以表征金属原子与石墨烯相互作用引起的电荷的重新分布,很明显地看出电荷从金属原子向碳原子转移,这与金属原子和碳原子之间的电负性差别是一致的.在图1(b)中可以看出电荷主要局域在C原子周围,显然,Li的s轨道和C的p轨道的杂化态是局域的,这反映了电荷从阳离子到阴离子转移的情况,Li和C原子之间形成了典型的离子键.从能带图4可以看出,Li的加入导致石墨烯的自旋劈裂,呈现金属性质,与其对应的态密度图相一致.

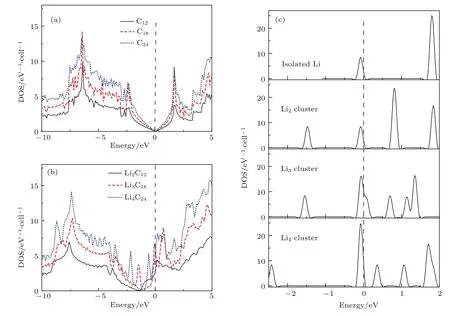
图2 (网刊彩色)(a)石墨烯(C12,C18,C24)的态密度图;(b)对应图1(a)中石墨烯吸附Li团簇(Li2C12,Li3C18,Li4C24)的态密度图;(c)孤立Li原子,Li2,Li3,Li4团簇的态密度图Fig.2.(color online)(a)The DOS of graphene(C12C18C24),and(b)Li cluster adsorbed on graphene(Li2C12,Li3C18and Li4C24),corresponding to Fig.1(a),respectively;(c)the DOS of isolate Li atom,and Li2,Li3,Li4clusters,corresponding to Fig.1(c),respectively.

图3 (网刊彩色)(a)—(d)分别为LiC6,Li3C18,Li4C24,Li5C30的DOS图和PDOS图,及孤立Li原子的DOS图Fig.3.(color online)(a)–(d)The DOS and PDOS of LiC6,Li3C18,Li4C24,Li5C30,and the DOS of isolated Li atom.

为了定量地计算Li原子/团簇向石墨烯实空间中转移的电荷数,我们采用Bader电荷分析法[28],得到体系中每个原子的电荷量,通过累加,进而可以得到总体系的电荷量.对于石墨烯吸附Li原子/团簇,通过计算吸附的Li原子/团簇前后电荷量的变化,即可得到向石墨烯转移的电荷量,如表1所列,LiC6,Li2C12,Li3C18,Li4C24,Li5C30,Li6C36中Li原子/团簇向石墨烯转移的总电荷数,由Bader电荷分析得知,转移的电荷∆Q分别为0.6493e,1.3405e,1.0664e,1.5102e,1.9128e,2.7814e.

3.2 石墨烯吸附锂团簇的热力学性质

在石墨烯吸附Li团簇的体系中,随着Li原子的数量增加,将可能形成团簇.为了计算Li团簇的形成能,在Li浓度为x时,定义团簇的形成能计算公式为

表1 各构型中Li原子的位置坐标(X,Y,Z)及Bader电荷分析结果,∆Q为Li原子/团簇向石墨烯转移的电荷数.Li-b代表低层分布的Li原子,Li-t代表顶层分布的Li原子Table 1.The Li atom position coordinates(X,Y,Z)of every models,and the charge analysis results by Bader,∆Q is the charge of Li atom/cluster transferred to graphene.Li-b and Li-t is Li atom in the bottom and the top layer of Li cluster adsorbed on graphene.

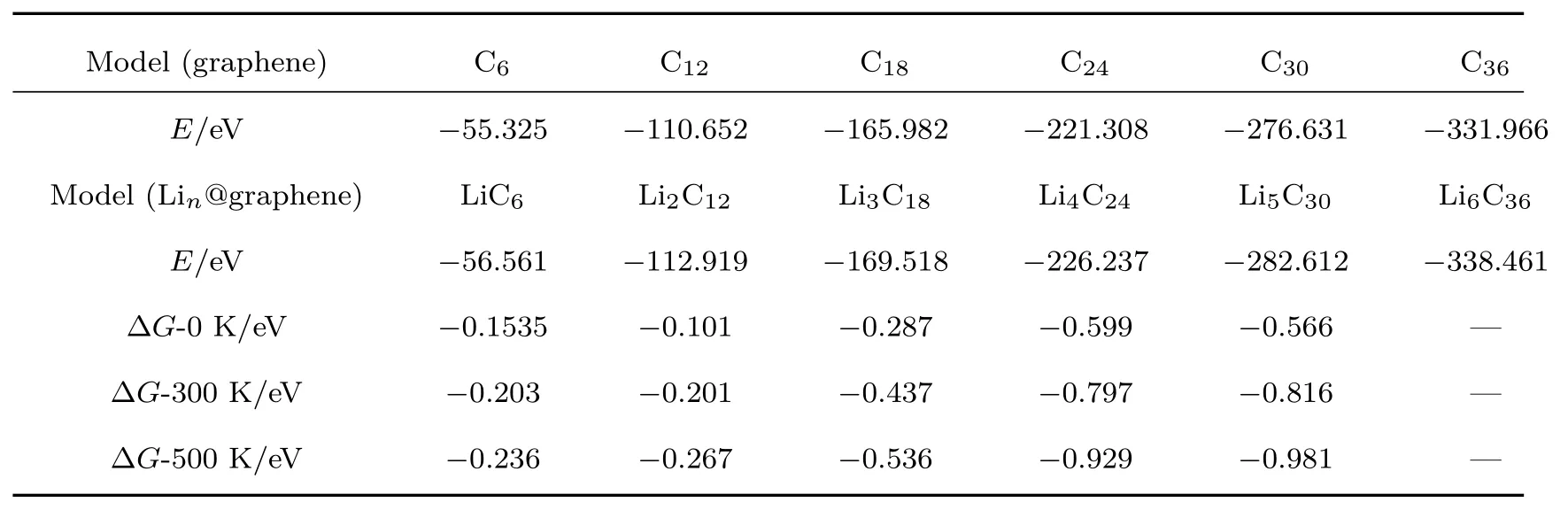
表2 石墨烯、石墨烯吸附Lin的能量及Lin在不同温度下的形成能∆GTable 2.The energy of graphene and Linadsorbed on graphene.∆G is the formation energy of Lin,under different temperature.

图4 (网刊彩色)(a)—(c)分别为Li2C12,Li3C18和Li4C24的能带结构图Fig.4.(color online)(a)–(c)The spin-up band and spin-down band structures of Li2C12,Li3C18Li4C24,corresponding to Fig.1(a).

E(Lin@graphene),E(graphene)分别为通过DFT理论计算得出石墨烯吸附Li团簇,及石墨烯的能量,µ(Li@LixC)是Li在任意浓度下的化学势,在锂离子电池中,Li原子会首先到达石墨烯表面,然后吸附到石墨烯上,使用吸附相作为参考,定义Li原子的化学势为计算公式(2),在成核过程中强烈依靠Li原子的化学势,由于团簇的构型熵远小于参考相的化学势,而被忽略.参考相的构型熵由一定浓度Li团簇的吸附构型所估算,S为熵值.计算团簇的形成能时,先将x=1/6代入热统公式(3),kB是玻尔兹曼常数,算出熵值S,将S值代入到(2)式,来计算化学式µ,将µ代入到(1)式中就可得出Li团簇的形成能.这里温度分别取0,300,500 K时,µ值分别为−1.083,−1.033,−1 eV/mol.需指出的是E(Lin@graphene)与E(LixC)含义不同,前者是基于DFT理论所计算的石墨烯吸附锂团簇体系总能量,相关的TS项,因S太小可忽略,其总能量随n而变化;后者为Li原子弥散分布在石墨烯表面的总能量,锂原子是随机分布,熵值较大,能量是固定的,与n无关,也就是锂原子随机分布在石墨烯上的宏观的能量.E(LixC)的含义为Li在任意浓度下的能量,建模型时,使Li尽可能分散地分布在石墨烯表面,改变1个Li原子的位置,达到有一定的混乱度的结果.又因为在固体中原子作用力尽可能小(石墨烯是主体,熵几乎为零,锂是掺杂),使得混乱度对内能的作用仅处于微扰.本文选取了Li6C36的能量近似代替E(LixC).通过(1)— (3)式[29]和表2中的计算数据,在一定Li浓度下计算了不同温度下的不同大小的锂团簇的形成能,见表2和图5中的点实线.从图5可看出,随Li原子个数增加,其形成能总体有升高的趋势,且形成能为负值,意味着容易形成Li团簇.在温度0,300,500 K时,随着温度的升高,形成能增加,意味着温度升高有利于团簇的形成.

图5 (网刊彩色)点实线为模拟计算值,通过(1)式,得出不同温度下的锂团簇的形成能;虚线为基于Wul ff定理,由(9)式得出,通过修改界面能γinterface,拟合点实线而成(x=1/6)Fig.5.(color online)Cluster formation energies at different temperature:symbols represent atomistic results,as given by Eq.(1);the dashed lines show thefitting of Eq.(9)by modifying the interface energy rinterface,based on the macroscopic Wul ffconstruction model.

我们用另一种方法即Wul ff定理,从理论上估算石墨烯上锂团簇的形成能.采用Wul ff定理的用意,是基于一种晶体生长的想法,从中也渗透出形核的想法.当晶体处于平衡态时,从晶体的中心到晶面的距离与该晶面的表面能成正比.相对于块体相,团簇的形成能公式为(4)式,与块体材料相比,团簇比表面积大,不能忽略.而增加的量可以看成是团簇比同粒子数的块体相增加的表面能,即形成能.使用DFT理论计算Li的(100),(110)和(111)晶面体系的能量Esys,及对应的相同原子数块体Li的能量Ebulk,A为晶面的表面积,γsurf为晶面的比表面能,由(5)式,我们得出了(100),(110)和(111)晶面的比表面能,γsurf分别为29.875,31.226,35.136 meV/Å2.通过以上理论计算可得出各方向的比表面能.根据Wul ff定理可计算各方向的表面积,如图6所示.

晶面(100)的表面积为2.348 Å2,λ值为1.269,通过DFT理论计算原胞Li中一个Li原子的能量为−2.281 eV,在常温300 K下的化学式µ值为−1.033 eV/mol.将各物理参数代入(6)式中,得出(9)式,其中γ(100)未知,需要拟合第一种方法得出的计算值,γ(100)约为137 meV/mol.图5中的虚线是利用Wul ff定理和(9)式拟合点实线得出.从图5中可以看出,当Li浓度为1/6时,在0,300,500 K,其形成能是升高的趋势,因此具有自发形成Li团簇的趋势,说明高Li浓度下,不适合做Li电池,会生长枝晶,引起电池的循环稳定性问题,甚至导致电池的失败,与实验结果比较符合.Harris等[22]从实验上原位观察得出,随着Li浓度的升高,Li板或Li枝晶的形成都能导致电池的失败;Tarascon和Armand[20]也曾经预测Li枝晶的问题.在不形成Li枝晶的前提下,增加石墨烯上吸附Li的数量,以提高储能密度.目前,石墨烯层数对于储锂性能的影响存在很大的争议,按理说单层石墨烯两个表面都暴露在外面可以很容易存储锂,进而得到高比容量的材料,但Pollak等[30]实验表明在单层石墨烯上Li之间会产生排斥力,和我们计算结果比较符合.通过拉曼光谱测试得出单层石墨烯能形成LiC20的结合,这样单层石墨烯的储锂容量显然比较低,我们理论预测的在单层石墨烯上Li/C比值应小于1/6,与拉曼光谱测试符合.理论计算和实验值的差距在于,目前虽然有多种制备石墨烯材料的方法,并且石墨烯材料的产量和质量都有了很大的提升,但对不同方法制备石墨烯材料的结构参数及表面官能团、结构缺陷、异质原子等如何影响其电化学储锂性能尚缺乏深入研究,因此,不同制备方法得出的石墨烯的能量密度值差距也很大.

图6 (网刊彩色)由Wul ff定理截成的多面体Fig.6.(color online)A polyhedron truncated by the Wul fftheorem.

4 结 论

采用第一性原理分析了锂团簇与石墨烯相互作用的机理.计算Li团簇与石墨烯吸附前后的DOS图、能带结构图、电荷密度分布图,并定量计算了Li团簇向石墨烯转移的电荷.阐明了Li团簇与石墨烯的相互作用,锂与碳形成离子键.并分析了锂原子吸附在石墨烯上形成团簇的热力学判据,运用热力学公式算出形成能,利用Wul ff定理得出带参数的成核公式,拟合实验值,并得到相应的理论公式,当Li:C=1:6时,有自发形成Li团簇的趋势,易形成Li枝晶.本研究对实验有一定的理论指导意义.

[1]Yoo E,Kim J,Hosono E,Zhou H,Kudo T,Honma I 2008Nano Lett.8 2277

[2]Lian P C,Zhu X F,Liang S Z,Li Z,Yang W S,Wang H H 2010Electrochim.Acta55 3909

[3]Jaber-Ansari L,Puntambekar K P,Tavassol H,Yildirim H,Kinaci A,Kumar R,Saldana S J,Gewirth A A,Greeley J P,Chan M K,Hersam M C 2014ACS Appl.Mater.Interfaces6 17626

[4]Zhao X,Hayner C M,Kung M C,Kung H H 2011ACS Nano5 8739

[5]Jang B Z,Liu C G,Ne ffD,Yu Z N,Wang M C,Xiong W,Zhamu A 2011Nano Lett.11 3785

[6]Wang D,Choi D,Li J,Yang Z,Nie Z,Kou R,Hu D,Wang C,Saraf L V,Zhang J,Aksay I A,Liu J 2009ACS Nano3 907

[7]Zheng J,Ren Z,Guo P,Fang L,Fan J 2011Appl.Surf Sci258 1651

[8]Lv W,Tang D M,He Y B,You C H,Shi Z Q,Chen X C,Chen C M,Hou P X,Liu C,Yang Q H 2009ACS Nano3 3730-6

[9]Wang G X,Shen X D,Yao J,Park J 2009Carbon47 2049

[10]Pan D,Wang S,Zhao B,Wu M,Zhang H,Wang Y,Jiao Z 2009Chem.Mater.21 3136

[11]Bhardwaj T,Antic A,Pavan B,Barone V,Fahlman B D J 2010Am.Chem.Soc.132 12556

[12]Ferre-Vilaplana A 2008J.Phys.Chem.C112 3998

[13]Froudakis G E 2001Nano Lett.1 531

[14]Garay-Tapia A M,Romero A H,Barone V 2012J.Chem.Theory Comput.8 1064

[15]Khantha M,Cordero N A,Molina L M,Alonso J A,Girifalco L A 2004Phys.Rev.B70 125422

[16]Chan K T,Neaton J B,Cohen M L 2008Phys.Rev.B77 235430

[17]Yang C K 2009Appl.Phys.Lett.94 163115

[18]Medeiros P V C,Mota F D,Mascarenhas A J S,de Castilho C M C 2010Nanotechnology21 115701

[19]Klintenberg M,Lebegue S,Katsnelson M I,Eriksson O 2010Phys.Rev.B81 085433

[20]Tarascon J M,Armand M 2001Nature414 359

[21]Mayers M Z,Kaminski J W,Miller III T F 2012J.Phys.Chem.C116 26214

[22]Harris S J,Timmons A,Baker D R,Monroe C 2010Chem.Phys.Lett.485 265

[23]Kresse G,Furthmüller J 1996J.Comput.Mater.Sci.6 15

[24]Blöchl P E 1994Phys.Rev.B50 17953

[25]Perdew J P,Chevary J A,Vosko S H,Jackson K A,Pederson M R,Singh D J,Fiolhais C 1992Phys.Rev.B46 6671

[26]Yang G M,Zhang H Z,Fan X F,Zheng W T 2015J.Phys.Chem.C119 6464

[27]Fan X F,Liu L,Kuo J L,Shen Z X 2010J.Phys.Chem.C114 14939

[28]Henkelman R,Arnaldsson A,Jonsson H J 2006Comput.Mater.Sci.36 354

[29]Liu M,Kutana A,Liu Y,Yakobson B I 2014J.Phys.Chem.Lett.5 1225

[30]Pollak E,Geng B,Jeon K J,Lucas I T,Richardson T J,Wang F,Kostecki R 2010Nano Lett.10 3386

PACS:73.20.At,81.05.ue DOI:10.7498/aps.66.057301

The first-principle calculation on the Li cluster adsorbed on graphene∗

Yang Guang-Min1)2)†Liang Zhi-Cong2)Huang Hai-Hua2)

1)(College of Physics,Changchun Normal University,Changchun 130032,China)
2)(College of Materials Science,Jilin University,Changchun 130012,China)

17 September 2016;revised manuscript

4 December 2016)

As a stable single sheet of carbon atoms with a honeycomb lattice,graphene has become attractive for its potential applications in electrochemical storage devices,such as anodes for rechargeable Li batteries.Since both sides of it can hold adsorbents,a graphene sheet is expected to have extra storage sites and therefore it has a possibly higher capacity than graphite.However,certain shortcomings of Li battery,such as instability lead to battery failure under overcharging or overvoltage conditions.The limit to capacity results in a short time of discharge.Thus,more attention should be paid to the stabilities of electrode materials,such as Li cluster nucleation on graphene leading to dendrite formation and failure of the Li-ion battery.In this work,we build a supercell model of single layer graphene with hexagonal structure,and then change the size of Li cluster which is used to be adsorbed on graphene,with keeping Li:C ratio at 1:6.Using the first principle based on density functional theory,we calculate the density of states,charge density difference and energy band structure.The interaction between Li and pristine graphene is studied in detail by analyzing the electronic properties and charge distribution of the isolated Li clusters and Li clusters adsorbed on graphene.It is found that the ionic bonding can be formed at the interface between Li clusters and graphene,and the charge transfer controls the interaction of the Li-carbon nanostructure.Combing thermodynamics method with the nucleation mechanism,the relationship between the cluster size and nucleation probability is analyzed,and the nucleation on graphene of Li with a certain concentration is also investigated.We estimate the nucleation barrier for Li on graphene and investigate the stability of Li adsorption on graphene by considering the effects of Li concentration and temperature.The Li concentration of 16.7%is considered for the formation of clusters with different sizes on graphene.With the size of Li cluster increasing,the cluster adsorbed on the graphene begins to be more stable than the single Li atom.The formation energy for the cluster is found to increase with the increase of temperature,and it is negative,meaning that Li cluster can be formed.It is expected that the corresponding calculation results from this atomistic simulation will shed some light on the in-depth understanding of Li-storage on graphene and the cycling stability and dendrite formation in Li-ion batteries with graphene-based materials serving as the anode.

graphene,Li clusters,electronic structure,first principle

PACS:73.20.At,81.05.ue

10.7498/aps.66.057301

∗长春师范大学自然科学基金(批准号:2015-010)资助的课题.

†通信作者.E-mail:yangguangmin@cncnc.edu.cn

*Project supported by the Natural Science Foundation of Changchun Normal University,China(Grant No.2015-010).

†Corresponding author.E-mail:yangguangmin@cncnc.edu.cn