多孔材料的温度和压强计算∗
2017-08-01陈俊祥于继东耿华运贺红亮
陈俊祥 于继东 耿华运 贺红亮
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理重点实验室,绵阳 621999)
多孔材料的温度和压强计算∗
陈俊祥†于继东 耿华运 贺红亮
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理重点实验室,绵阳 621999)
(2016年10月11日收到;2016年12月6日收到修改稿)
多孔材料内部含有大量孔隙,孔隙一旦塌陷就回归为密实物质.但孔隙塌陷沉积的能量将提升基体材料的温度,导致热力学状态量发生变化.尤其是在冲击波压缩下,多孔材料的温升很高,温度变化对其他热力学状态量的变化影响很大,因此解决多孔材料的温度计算是不可回避的问题.本文在研究Grüneisen通用函数γv(v)的基础上,将密实材料的德拜温度函数通过数学的方法,延拓到多孔材料的密度范围,建立了多孔材料的等效德拜温度函数Θ(v);并据此推导出了多孔材料的等熵温度函数Ts(v).再借鉴多孔材料0 K等熵功相等的假设,建立了多孔材料与密实材料在相等压强下等熵功相等的计算模型,给出了多孔材料的等熵压强函数ps(v).于是,齐备了冲击波压缩下多孔材料温度和压强计算的参考方程,即温度方程Ts(v)和压强方程ps(v).为了检验本文方法的有效性,以Cu为例计算了孔隙度m=1.13,1.22,1.41,1.56,1.98等5种多孔材料的冲击压强和冲击温度,计算结果与实验数据相符较好.同时,用其他方法做了计算,两种方法计算结果的比较,显示出本文计算方法的可靠性.
多孔材料,孔隙度,德拜温度,等熵函数
1 引 言
多孔材料在许多工程领域中有着广泛的应用[1−5],但在冲击压缩下多孔材料孔隙塌缩区没有相应的热力学物性参数,无法估算冲击压缩对多孔材料的温度影响.另一方面,多孔材料在冲击压缩下升温升压都特别高,这对于研究高温高压下物质的性质,又是一个重要的手段[6−10].
目前对多孔材料已有多种计算冲击压强的方法,但都是用密实材料的压强作参考,并假设密实材料的物性参数与温度无关.这些计算结果在高压区与实验数据相差较大,甚至在某些压力区还有趋势性的错误.如p-v(压强-比体积)曲线的斜率出现反转的现象.
本文在文献[11]的基础上,将密实材料的德拜温度函数延拓到多孔材料的密度范围,构建了多孔材料的等效德拜温度函数,并提出了一种新的计算模型,比较准确地计算了多孔材料的压强与温度,为多孔材料的高温高压物性计算提供了一种比较好的方法.
2 多孔材料物态方程
Bosho ff-Mostert和Viljoen[12]对现有计算多孔材料Hügoniot方程的方法做了评述,文中列出的5种计算方程基本上可以分为两类:一类是Grüneisen方程,式中∆表示多孔材料与密实材料物态量之差,γv(v)是振动Grüneisen系数,E(v)是比内能;另一类是W-J方程,式中R(p)是W-J系数,H(p)是比热焓.这两类方程都是以密实材料的压强方程作参考,用密实材料的振动Grüneisen系数γv(v)进行计算(W-J系数R(p)由γv(v)换算).两类方程基于相同的热力学原理,相同的热力学参数,只是对参数的简化程度不同,所以计算结果大同小异.这两类方程都没有考虑温度的影响,而多孔材料的特点恰恰是冲击压缩中不可忽视的高温变化,所以这两类方程在高压区计算结果与实验不符.
2.1 多孔材料物态方程的新探索
多孔材料的特点是p0(初始压强),T0(初始温度),E00(初始比内能)都与密实材料相同,只有v00(初始比体积)不同.由密实材料的粉末烧结成多孔材料,物质晶粒的微观构造并没有发生变化,只是晶界之间形成了孔隙.孔隙增加了晶粒的表面积,但增加的表面能极少,与比内能相比可以忽略.多孔材料的初始比内能等于密实材料的初始比内能,E00=E0.
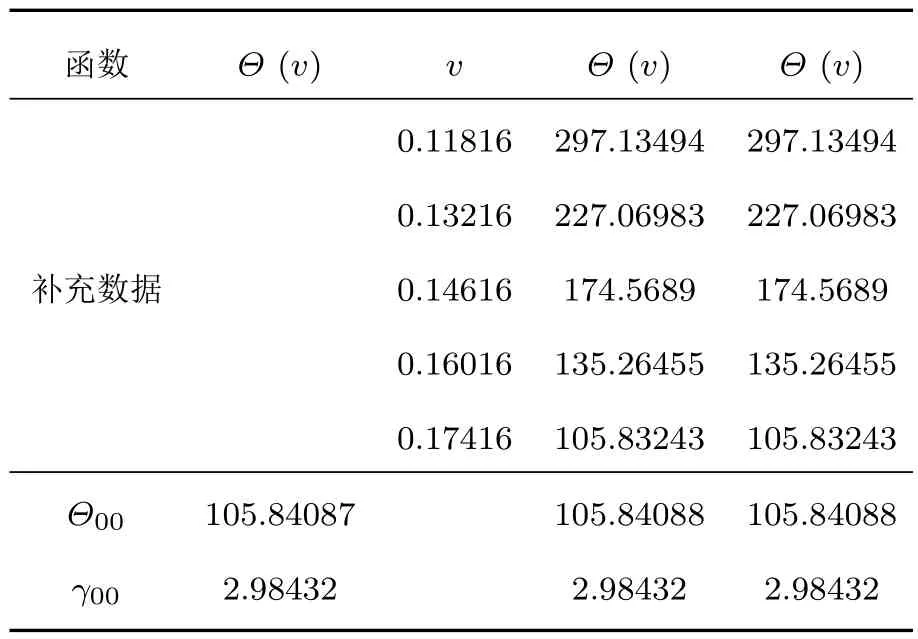
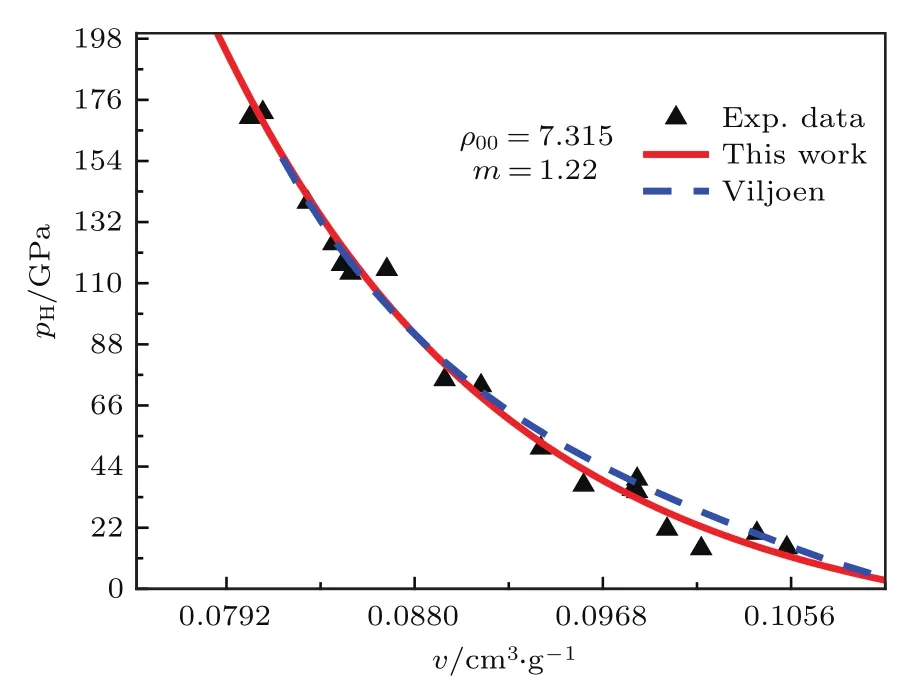
多孔材料的初始比体积v00没有固定值,可以做成各种不同v00的多孔材料.多孔材料的孔隙度m=v00/v0.现有实验资料中,许多m<2的多孔材料的冲击压缩实验数据,都在v 等熵压缩的比内能与温度无关,Es(v)=下标s表示熵.设多孔材料的等熵压强函数为psm(v),比内能函数为Esm(v),下标m表示孔隙度.在v00—v0区间,psm(v)=0,又E00=E0,故 由此可见,多孔材料在孔隙闭合后的等熵压强线与密实材料的等熵压强线完全相同.于是多孔材料的等熵压强函数可分成两段表述: 2.2 多孔材料的等效德拜温度函数 德拜温度函数只与物质晶格的比体积有关.由密实材料形成多孔材料,物质内部的晶格并没变,但晶格外部形成了孔隙.孔隙塌陷虽不影响晶格的微观结构,但晶格表面的温度发生变化.物质的热力学温度与晶格的德拜温度函数紧密相关,为了计算多孔材料孔隙塌陷的温度变化,需要有一个与多孔材料比体积收缩等效的德拜温度函数.这个函数在孔隙闭合阶段随v而变化,孔隙闭合后与密实材料的德拜温度函数相同.为此,可将密实材料的德拜温度函数Θ(v)的起点v0延拓到v00,做出多孔材料的等效德拜温度函数. 在研究γv(v)通用函数[11]的工作中,已经提出了密实金属材料的德拜温度函数可表示为 式中ρ0是材料的初始密度,Θ0是材料的初始德拜温度,γ0是材料初始比体积为v0时的Grüneisen系数.Θ0与γ0的量值由测量Θ(v)的实验数据按(2)式拟合确定.不同的ρ0拟合出不同的Θ0与γ0.由此可见,若以密实材料Θ(v)的实验数据为基础,在v0与v00之间补充若干实验数据,将(2)式的初始密度改为ρ00,再对实验数据进行拟合,便可得到多孔材料的Θ00与γ00,从而做出多孔材料的等效德拜温度函数. 以下以Cu为例,给出求解ρ00=5.742 g/cm3Cu的等效德拜温度函数的方法. 第一步,计算Cu密实材料Θ(v)的数据记入表1. 表1 密实Cu的德拜温度数据Table 1.Debye temperature data of compact Cu. 第二步,设ρ00=5.742 g/cm3的多孔材料德拜温度函数为 用(3)式拟合表1中的数据,得出Θ00和γ00的初步数据,记入表2第2列. 表2 多孔材料Cu(ρ00=5.742 g/cm3)德拜温度函数拟合数据Table 2.Debye temperature function fitting data of porous coppor(ρ00=5.742 g/cm3). 第三步,在v0至v00之间内插5个比体积v的取值点(如表2第3列),将第二列的Θ00和γ00代入(3)式,计算5个内插点Θ(v)的补充数据,记入表2第4列. 第四步,将表2第4列的5个Θ(v)补充数据加表1中的Θ(v)数据,再用(3)式拟合,得出表2第4列的Θ00和γ00. 第五步,用第4列的Θ00和γ00代入(3)式,计算出表2中第5列的5个Θ(v)补充数据,再加表1中的Θ(v)数据,拟合得出第5列中的Θ00和γ00.如此反复,直至拟合的的Θ00和γ00不变为止. 依此方法,做出文献[13]发表的5种多孔Cu材料的等效德拜温度函数分别为: 图1是上述5种多孔Cu材料的Θ(v)函数线.曲线最前部分是密实Cu的德拜温度线,之后为不同初始密度多孔材料Θ(v)线的延伸段.各Θ(v)延伸段的向前部分是相互重合的. 图1 不同密度Cu的德拜温度函数Fig.1.Debye temperature of copper with different porosity. 3.1 低孔隙度材料的等熵温度函数 参照文献[11]求解等熵温度函数的方法,以ρ00=5.742 g/cm3多孔Cu为例,做法如下. 计算中取用Cu的物性参数及公式:Cu的气体常数 电子比热系数β(v)=4.7274×10−8v2/3kJ/(g·K2),电子γ系数γe=2/3,晶格等容比热Cv(v,T)=3RD(v,T)+β(v)T,晶格热力学γ函数: 多孔Cu的密度ρ00=5.742 g/cm3.多孔Cu的等效德拜温度函数Θ(v)和Grüneisen系数γv(v)如下: 设ρ00=5.742 g/cm3多孔Cu的等熵温度函数为 式中的γs0=γ(v00,T0)是已知的.另一方面等熵温度的热力学方程为 (6)式右端γ(v,T)中的温度变量T即(5)式等熵温度函数Ts(v).(5)式与(6)式在v00点的1,2,3阶导数相等,即可解出m,n的値.经过计算得到: 3.2 低孔隙度材料冲击温度和压强计算 设E00=0,在v00至v0的孔隙区,根据(1)式,多孔材料的pms(v)=0,Ems(v)=0. 此方程中γ(v,T)0,v00−v̸0,两端相等只有pH(v)=0.故只需做v6v0区域的计算. 根据(1)式,在v6v0区域,多孔材料的等熵压强用密实材料的等熵压强函数.取用文献[13]密实Cu的Hügoniot数据,换算得到密实Cu的等熵压强函数为 (8)式经文献[14]100 GPa之内的等熵实验数据验证完全相符,且可用于更宽的压力区. 设E0=E00=0,建立ρ00=5.742 g/cm3多孔Cu在v6v0区域的Hügoniot方程组如下: 由于EH(v,T)=EH(v),pH(v,T)=pH(v),代入(9)式整理后可得到 (10)式中ps(v)和Ts(v)是已知函数,v是自变量,可解出T.将解出的T与v代入方程组(9)的第一式,即可算出pH(v,T).从而联立方程组(9)同时计算出多孔Cu材料在Hügoniot状态下的压强和温度. 3.3 与其他方法的比较 文献[12]评述中认为Viljoen方法是目前计算多孔材料Hügoniot压强最好的方法.Viljoen方法以密实材料的Hügoniot压强函数ph(v)和0 K压强函数pc(v)做计算的参考方程,用W-J方程求解多孔材料的Hügoniot压强pH(v).W-J系数定义为其中H(p,v)是物质的比热焓,H(p,v)=E(p,v)+pv. 由于R只是p的函数,沿等压路径R的取值相同.若p(vc)为冷压线,p(vh)为密实材料Hügoniot压强线,p(vH)为多孔材料Hügoniot压强线,则 Viljoen用如下密实Cu的ph(v)和pc(v)函数代入方程(11),算出了多孔Cu的p-vH数据. 本文方法计算结果与Viljoen方法计算结果的比较见图2—图6. 从图中两种方法的计算结果比较,可以看出几点差异: 图2 ρ00=7.9 Cu冲击压缩p-v线Fig.2.Shock compression p-v curve of porous copper(ρ00=7.9). 图3 ρ00=7.315 Cu冲击压缩p-v线Fig.3.Shock compression p-v curve of porous copper(ρ00=7.315). 图4 ρ00=6.326 Cu冲击压缩p-v线Fig.4.Shock compression p-v curve of porous copper(ρ00=6.326). 1)对同一孔隙度,本文方法在实验压力区一致符合,Viljoen方法在低压区符合较差; 2)对不同孔隙度,本文方法适应性较好,Viljoen方法对孔隙度越大越不适应; 3)本文方法用含温度的物性参数计算,p-v线斜率按物理规律平滑过渡,Viljoen方法用不含温度的简化物性参数计算,出现p-v线斜率扭曲甚至反转的不合理现象; 图5 ρ00=5.742 Cu冲击压缩p-v线Fig.5.Shock compression p-v curve of porous copper ρ00=5.742). 图6 ρ00=4.508 Cu冲击压缩p-v线Fig.6.Shock compression p-v curve of porous copper(ρ00=4.508). 4)本文方法先计算温度,根据温度高低可以判断被压缩物质是否进入熔化区.孔隙度越大温度变化越大,孔隙度越大的实验数据分散性越大.大孔隙度包括初始点全区域的横坐标太紧密,容易掩盖数据的分散性,如图6(a).而在6(b)中,横坐标只取到有关的几个数据区,数据的分散性就非常明显.按固态计算的点线(pHS)全部高出实验数据.查看ρ00=4.508 g/cm3的温度计算数据,发现孔隙闭合时温度已高于熔化温度;于是改按液态方程计算,得到如图6(b)中的实线,便与实验数据的趋势一致.而6(b)中的虚线是按Viljoen方法计算的,不仅全部高于实验数据,而且出现由膨胀向压缩反转的异常现象.明知不合理也无法改变. 图7 多孔Cu冲击压缩T-p线Fig.7.Shock compression T-p curve of porous copper. 5)本文方法由联立方程组(9)解出冲击温度,再用解出的温度计算冲击压强,经实验数据检验,计算的压强与冲击压缩实验数据相符,则证明图7中的冲击温度线是可信的. 利用延拓德拜温度线的方法,补充多孔材料的物性参数,可以做出多孔材料在全压缩区的等熵温度函数.再利用密实材料的等熵压强函数,就可建立多孔材料在密实材料压缩区的p(v,T)方程组.这种p(v,T)方程组不仅可以计算Hügoniot物态量,而且还可以计算o ffHügoniot态的物态量和各种物性参数,是一种简便易行的好方法. 本文以Cu为例,发现孔隙度m=1.98的多孔材料孔隙闭合时的温度已超过熔化温度,需要按液态方程计算才可能与与实验数据趋势相符.因此,延拓德拜温度函数的方法只能适用到孔隙度m=2左右.当孔隙度m>2以后,由于密度太稀,延拓德拜温度线就没有意义了. [1]Liu P S 2004Introduction to Porous Materials(Beijing:Tsinghua University Press)(in Chinese)p16[刘培生2004多孔材料引论(北京:清华大学出版社)第16页] [2]Gibson L J,Ashby M F 1999Cellular Solids:Structure and Properties(Cambridge:Cambridge University Press)p8 [3]Zhao X F,Fang Y 2006Acta Phys.Sin.55 3785(in Chinese)[赵信峰,方炎 2006物理学报 55 3785] [4]Zhang H W,Li Y X 2007Acta Phys.Sin.56 4846(in Chinese)[张华伟,李言祥 2007物理学报 56 4864] [5]Rosa M E 2008Phil.Mag.Lett.88 637 [6]Tan H 2007Introduction to Experimental Shock-Wave Physics(Beijing:National Defence Industry Press)p56(in Chinese)[谭华 2007实验冲击波物理导引 (北京:国防工业出版社)第56页] [7]Jing F Q 1986Introduction to Experimental Equation of State(Beijing:Science Press)p134(in Chinese)[经福谦1986实验物态方程导引(北京:科学出版社)第134页] [8]Li X J,Gong Z Z,Liu F S 2001J.of High Press.Phys.15 221(in Chinese)[李西军,龚自正,刘福生2001高压物理学报15 221] [9]Li X J,Gong Z Z,Jing F Q 2001Chin.Phys.Lett.18 1632 [10]Wu Q,Jing F Q 1996J.Appl.Phys.80 4343 [11]Chen J X,Yu J D,Li P,He H L 2015Acta Phys.Sin.64 086401(in Chinese)[陈俊祥,于继东,李平,贺红亮2015物理学报64 086401] [12]Bosho ff-Mostert L,Viljoen H J 1999J.Appl.Phys.86 1245 [13]Marsh S P 1980LASL Shock Hugoniot Data(Berkekeley American:University of California Press)p62 [14]Wang G J,Luo B Q,Zhang X P,Zhao J H,Che S W,Tan F L,Chong T,Mo J J,Wu G,Tao Y H 2013The Review of Scientific Instruments84 015117 PACS:64.30.Ef,05.70.Ce DOI:10.7498/aps.66.056401 Temperature and pressure calculation of porous materials∗ Chen Jun-Xiang†Yu Ji-Dong Geng Hua-Yun He Hong-Liang (National Key Laboratory of Shock Wave and Detonation Physics,Institute of Fluid Physics,China Academy of Engineering 11 October 2016;revised manuscript 6 December 2016) Porous material contains a large number of pores,and once the pore space collapses,it changes into a dense material with the great increase of temperature because of the energy deposition by porosity collapsing.In the process of shock compression,the temperature is extremely increased,which influences the thermodynamic state of porous material significantly.Therefore,the calculation of temperature is important for the shock compression of porous material,yet it has not been solved well in the literature.In this paper,based on the study of Grüneisen general functionγv(v),the Debye temperature function of solid material is extended to the region of porous material,and the equivalent Debye temperature functionΘ(v)of porous material is formulated,from which the isentropic temperature functionTs(v)of porous material is obtained.Furthermore,a computation model is established,in which the isentropic work of porous is assumed to be equal to that of compact material under the same pressure at 0 K.With this model,the isentropic pressure functionps(v)of the porous material is acquired.Hence,the reference equation for calculating temperature and pressure of porous material,i.e.,Ts(v)andps(v),is completed.To demonstrate this method,thep-vandT-vcurves of the Hügoniot state of porous copperare computed,and the values of porosity arem1.13,1.22,1.41,1.56 and 1.98,respectively.The calculated results are in good agreement with the experimental data.A comparison with other calculation is also made,indicating a better reliability of the present method. porous material,porosity,Debye temperature,isentropic equation PACS:64.30.Ef,05.70.Ce 10.7498/aps.66.056401 ∗国家自然科学基金(批准号:11302202)和中国工程物理研究院科学技术发展基金(批准号:201402084)资助的课题. †通信作者.E-mail:cjx621@163.com *Project supported by the National Natural Science Foundation of China(Grant No.11302202)and the Foundation of President of China Academy of Engineering Physics(Grant No.201402084). †Corresponding author.E-mail:cjx621@163.com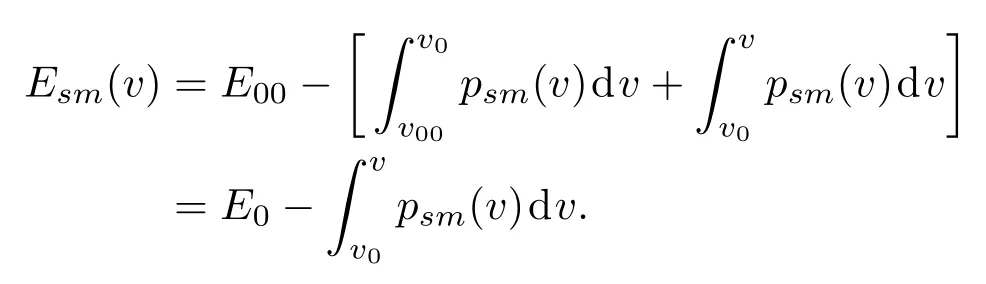
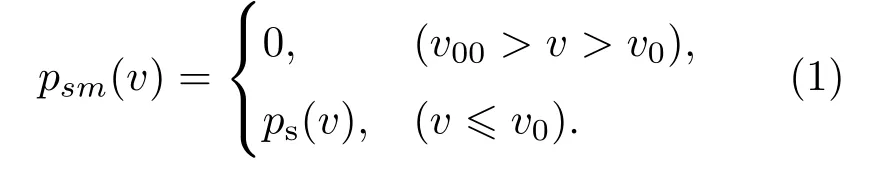
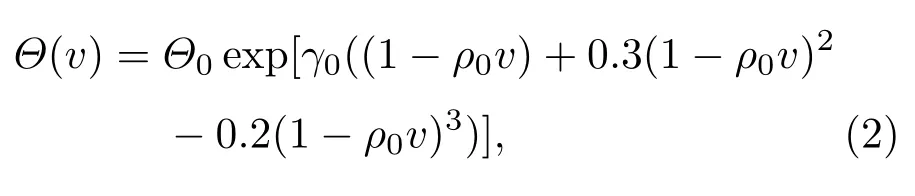






3 低孔隙度材料的温度和压强计算
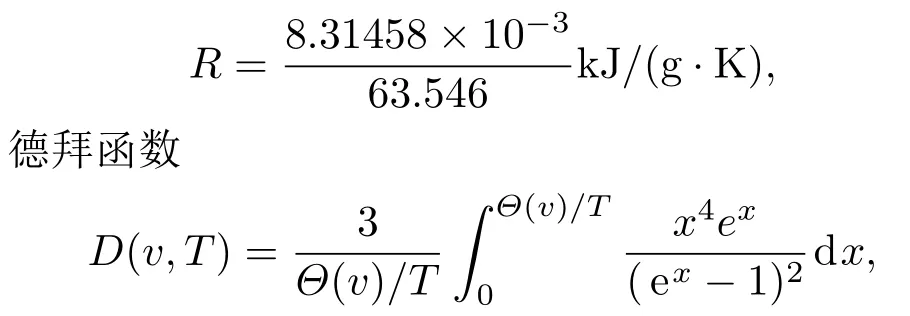
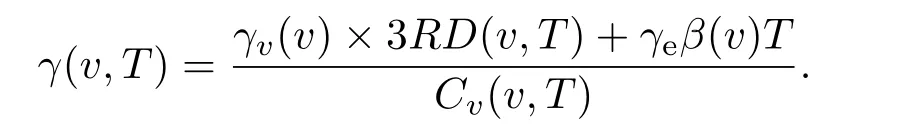


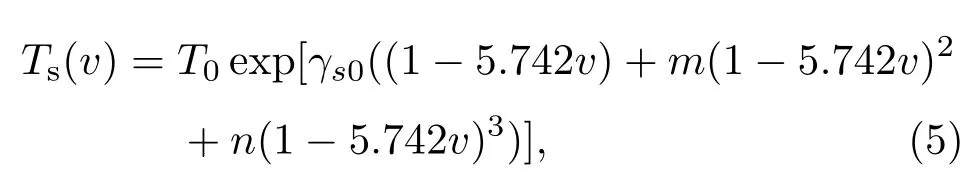

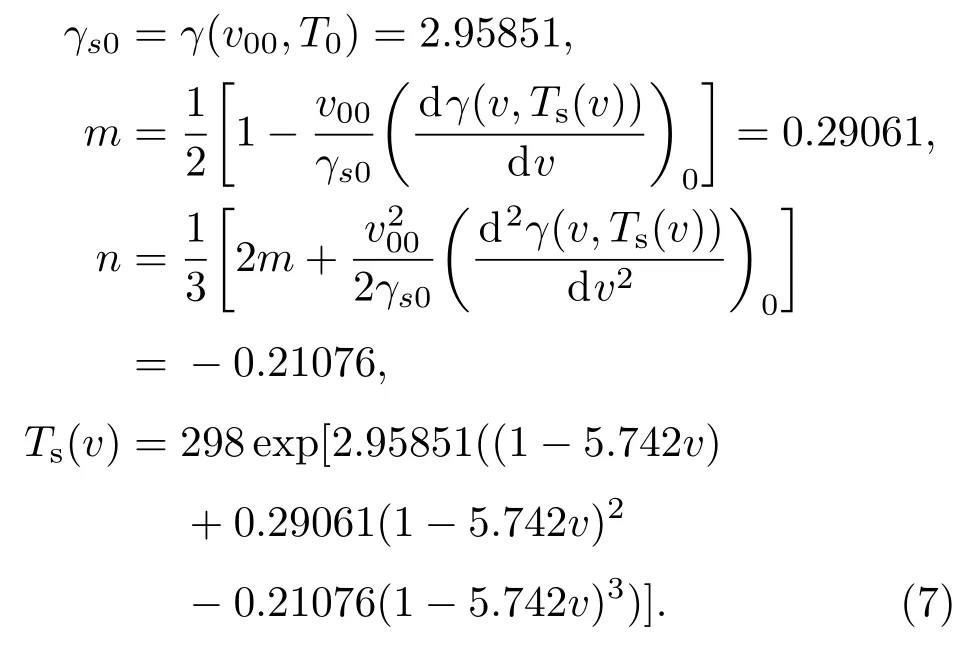
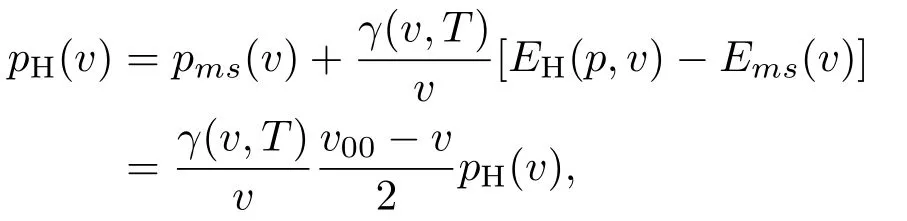


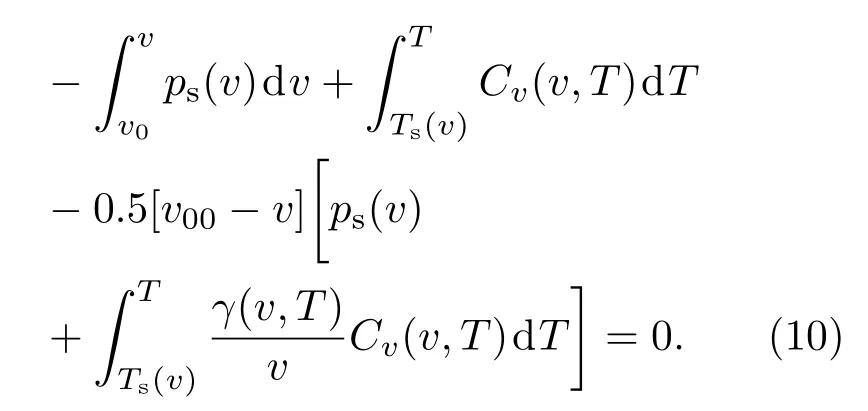
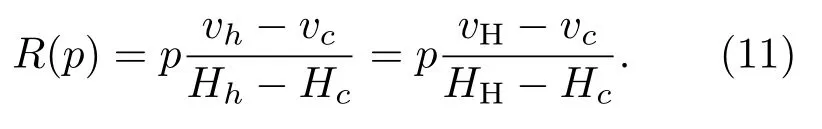


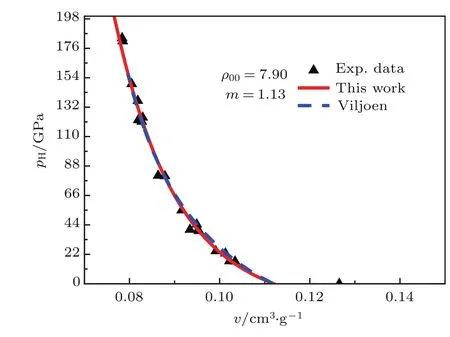




4 结 论
Physics,Mianyang 621999,China)
