一种功率可调的恒功率电源

吴高阳，鲁刚，王红波,韦熹

(广西大学电气工程学院，广西 南宁 530004)

一种功率可调的恒功率电源

吴高阳，鲁刚，王红波,韦熹

(广西大学电气工程学院，广西 南宁 530004)

恒功率电源是开关电源中的一种特殊电源，因其具有恒功率输出特性而得名。传统的恒功率电源存在着稳态性能差、设备利用率低和效率低等问题。研究表明，恒功率输出的Boost变换器是一个微分平坦系统。基于微分平坦理论设计的反馈控制系统有效地将非线性系统转化为线性系统，从而简化了设计过程，并且具有良好的动态性能和静态指标。本文以Boost变换器为例，基于微分平坦理论设计出控制策略。最后，研制了一台300W的Boost PFC电源样机，该恒功率电源的各项性能满足设计要求，具有较好的稳态和动态性能，实现了恒功率输出且功率可调功能。实验结果验证了控制策略的可行性与正确性。

微分平坦；恒功率电源；Boost变化器；控制策略

1 引言

不同应用领域对电源的要求也不同。按电源的输出特性分类，直流电源可分为恒压源、恒流源以及恒功率源。所谓恒功率源是指输出功率恒定的电源，其输出电压电流连续调节，但在工作范围内功率恒定不变。在一些特殊应用场合，比如某些测试电源[1]、显像管测试电源[2]以及焊接电源[3]等均为恒功率源。可见研发一个具有良好的静态和动态响应、稳定可靠以及高效的恒功率源是很有必要的。

基于微分平坦理论设计的反馈控制系统，有效的将非线性系统转化为线性系统，而且具有稳定性、快速性和鲁棒性等优点。文献[4]提出微分平坦非线性控制方法。文献[5]研究表明DC/DC变换器均属于微分平坦系统，而且与传统的PI调节器相比，平坦系统具有更好的动态性能。文献[6]表明级联系统属于微分平坦系统，且具有良好的稳定性。文献[7]研究表明AC/DC变换系统属于微分平坦系统，利用Lyapunov设计的控制系统具有稳定、快速以及高效的特性。

本文应用Lyapunov稳定性原理，将微分平坦理论应用于Boost恒功率源的控制。文中首先给出Boost变换器的大信号模型，而后证明Boost恒流源是一个微分平坦系统，由Lyapunov稳定性原理设计出控制策略。最后，通过实验验证了恒功率微分平坦控制策略的可行性与正确性。

2 恒功率微分平坦建模与控制

2.1 Boost恒功率平坦模型

图1为Boost电路的结构图。我们应用状态空间平均法对Boost变换器进行大信号建模，不难得出输入电流和输出电压对占空比的关系，如式(1)。

(1)

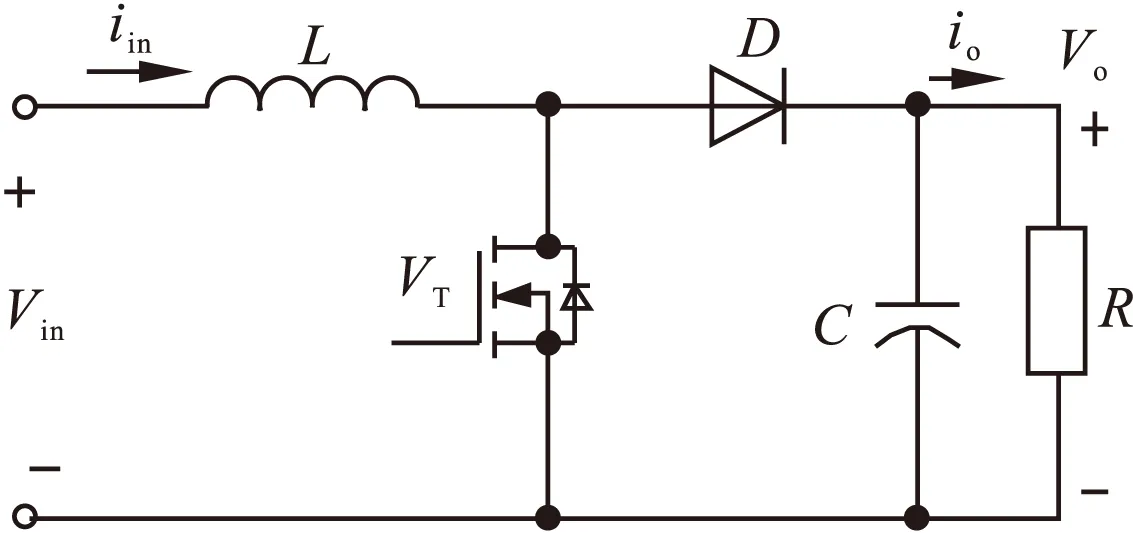
图1 Boost电路结构图

在本文中，是通过控制输入功率而达到输出功率的目的，同时又使得输入电流跟踪输入电压，实现功率因数校正(PFC)功能。以Pref为功率基准值，Pref可看做一个常量。通过对输入电压采样可得Boost PFC输入功率基准的瞬时值yd

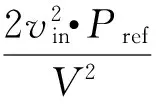
(2)

其中,V为输入交流电压的幅值，输入电压Vin为交流电压整流之后的半波正弦信号。取输出功率作为平坦输出。理想条件下，假设系统的效率为1，则平坦输出定义和瞬时输入功率一样，可表示为

y=h(x,u)=vin·iin

(3)

其中，定义系统变量x=iin，控制输入u=d。为了说明系统是微分平坦系统，控制输入u和状态变量x必须由平坦输出y表示，系统状态变量x根据平坦输出y方程变换得

(4)

通过对(3)式求导并且结合(1)式可得

(5)

由式(4)、(5)可知，x和u都可由y或其有限阶微分表示，故证明了恒功率输出的Boost PFC系统是一个微分平坦系统[1]。

2.2 恒功率微分平坦系统控制率的设计

微分平坦系统的控制归根结底还是基于误差信号的控制，根据Lyapunov稳定性原理设计控制器，定义跟踪误差变量为

(6)

(7)

其中，y是瞬时输入功率采样信号，e2为输入功率误差信号，e1为误差信号的积分。

为获得系统控制律，定义微分平坦控制系统的Lyapunov函数为

(8)

其中k1，k2为大于零的常数。同时，为满足Lyapunov稳定性原理，建立导函数为

(9)

其中k3为大于零的常数，对式(8)中的V(e1，e2)求导且其与(9)式相等得

(10)

结合(1)、(10)等式，可得到微分平坦系统控制律为

(12)

通过变量k1，k2，k3参数的选取，可以得到不同符合要求的控制律。本文取k1=k2=0.5，k3的取值由仿真的结果确定。根据所提出的控制率，可以得到恒功率输出Boost PFC的系统框图，如图2所示。

图2 控制框图

3 仿真

为了验证控制规律的正确性和可行性，本文例用MATLAB进行仿真。仿真参数为：输入交流电压幅值Vin=100V，输入电压工频频率为fb=50Hz，开关频率fs=100kHz，电感L=1mH，输出电容Co=1000μF，控制器参数k1=0.5，k2=0.5，k3=5×107。

3.1 稳态输出仿真

稳态输出仿真主要是为了验证其稳态指标。输入电压幅值为100V，以100Ω的电阻作为负载，取不同的基准功率Pref进行仿真。仿真结果如下。

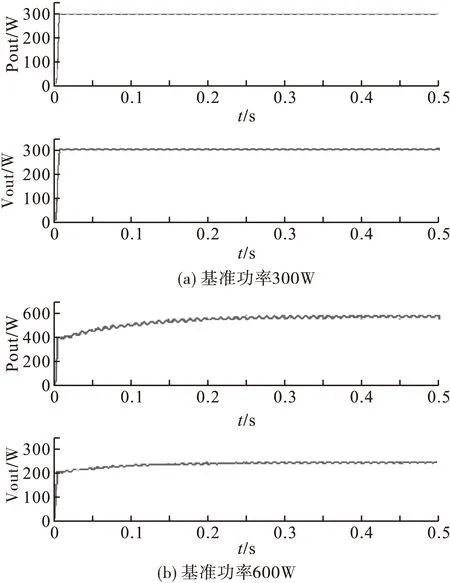
图3 输出功率及电压波形

如图3(a)所示，当基准功率为300W时，系统在0.01s内达到稳定输出，输出电压为173V，功率约为297W。如图3(b)所示，系统响应时间稍长，在0.2s左右达到稳定输出，输出电压为244V，输出功率约590W。由于仿真中模型中的场效应管和电感等元器件不是理想的，所以会产生损耗，设计符合要求。由图可知，系统具有良好的稳态性能。

3.2 动态性能仿真

系统动态响应特性主要通过跳变仿真实验检验，本文做了两组实验：一是基准功率不变，改变负载电阻；二是负载电阻不变，改变基准功率。

如图4(a)所示，基准功率为300W，负载为100Ω时，输出电压为174V，输出功率约为300W；当负载突变到50Ω时，经过0.2s，输出电压降为124V左右，输出功率重新稳定，约300W。如图4(b)所示，负载不变，当基准功率从300W跳变到600W时，输出功率由原来的300W经过0.2s后达到600W新的稳定点。可见，系统在负载或者基准功率发生跳变时是稳定的，达到改变输出功率的目的。

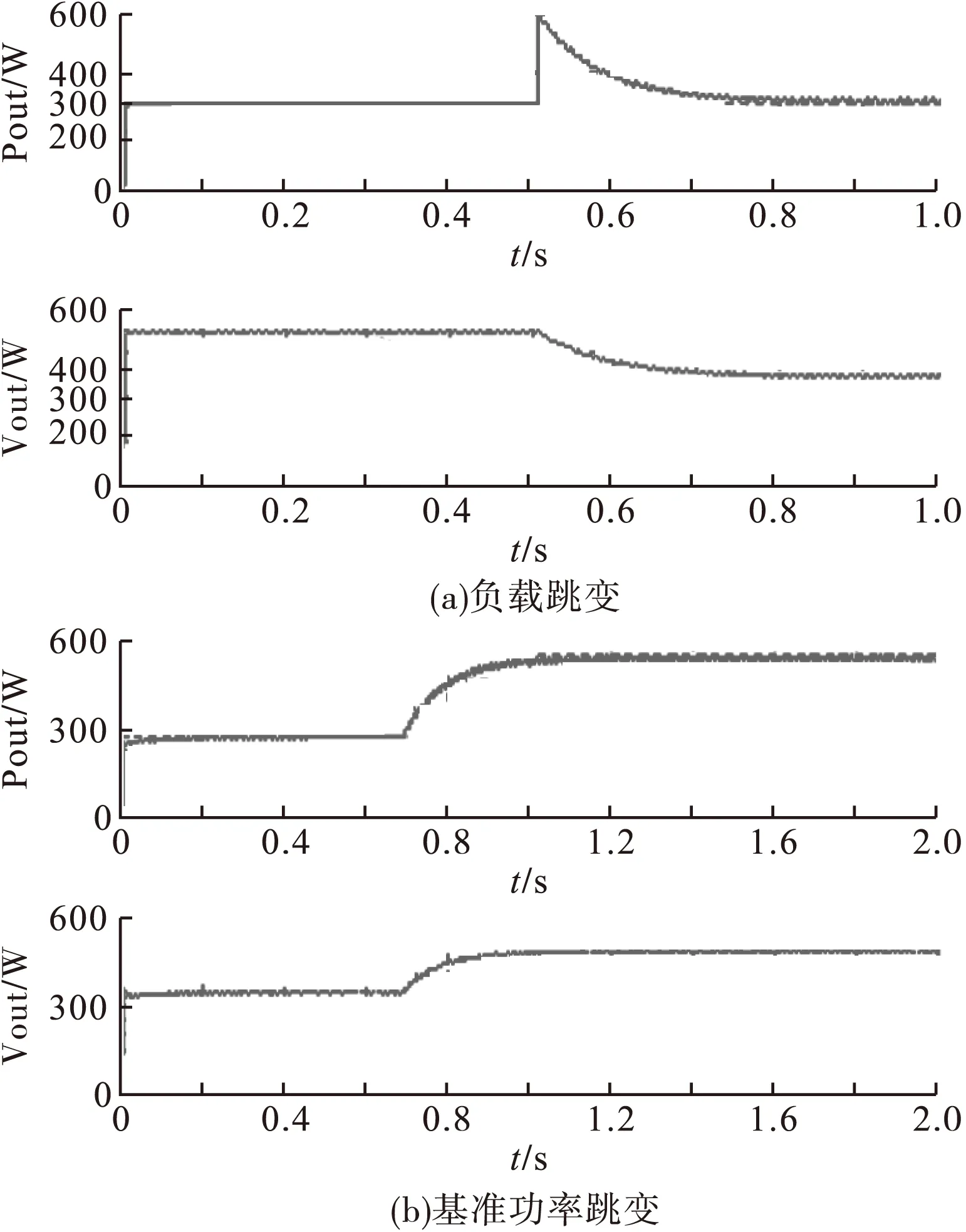
图4 输出功率及电压波形

4 实验结果与分析

为了验证提出的控制策略。设计出一台基于F2812控制的Boost变换器样机，其交流输入电压为85～240V,最大输出功率为300W，输出直流电压为250～400V，开关频率为60kHz。主电路升压电感取为L=1.1mH，开关管为IRF460型的MOSFET管，输出二极管为APT3060型快速恢复二极管，输出电容为1000uF/450V的电解电容。

4.1 基准功率跳变实验

图5为基准功率Pref跳变时的输入电压电流实验波形。图5(a)基准功率变大的实验波形，在输入交流电压有效值为85V条件下，基准功率Pref由150W跳变到300W。图5(b)是5(a)的逆过程。

由图可知：(1)系统输入电流呈正弦波形状，并且与电压同相位，功率因素接近于1，可知系统实现了PFC功能并且效果良好。(2)在基准功率跳变时，输入电压不变，输入电流在1～2个工频周期内达到原来的两倍，使输入功率达到基准功率设定值。由此可见，系统具有较好的动态响应和静态指标。

4.2 负载跳变实验

负载跳变实验波形如图6所示。图6(a)为负载电阻增大时的输出波形，负载由300Ω跳变到480Ω，图6(b)是6(a)的逆过程。

由图6(a)可以看出，负载跳变瞬间输出电流迅速减小，输出电压在50ms内由300V上升到380V，使输出功率保持恒定，约300W。输出电压在调整过程中未出现超调。表明系统稳定且具有良好的动态响应能力。

图5 基准功率突变时的输入电压电流波形

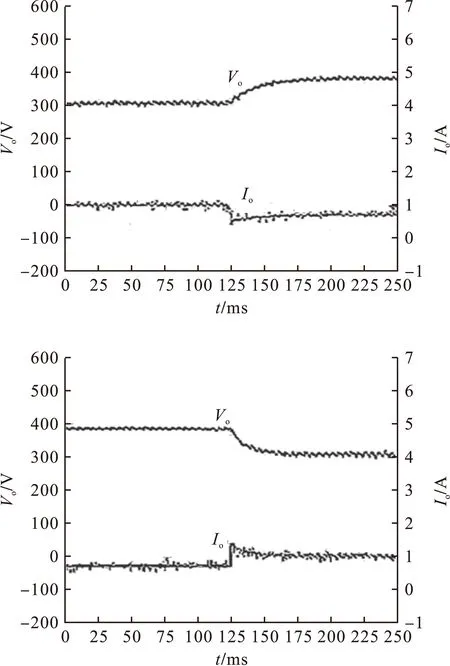
图6 负载电阻跳变时输出电流与电压波形

图7为恒功率源在改变基准功率条件下的效率曲线，表明系统效率较高，整个工作范围内可达到92%以上。

图7 效率曲线

5 总结

本文通过对Boost变换器建模分析,基于微分平坦理论的控制方法，用李雅普诺夫稳定性原理设计出恒功率输出系统的控制策略。仿真和实验验证了控制策略的可行性与正确性。电路很好地实现了恒功率输出以及PFC功能，而且可以通过改变基准功率来改变输出功率，实现一源多用的作用；在负载变换时，能够具有良好的稳定性和动态响应能力；系统效率较高，整个工作范围内可达到0.92以上。

[1] 周平.基于类功放的宽范围可调开关电源[J].电源技术应用,2004,7(11):646-651.

[2] 刘华毅,李霞,徐景德.基于单片机的宽范围连续可调直流稳压电源[J],电力电子技术，2001,35(6):7-9.

[3] 杨通,黄延龄,张光先.数字化的逆变弧焊电源[J].电焊机,2009,39(2):11-17.

[4] Fliess M,Levine J,Martin.Flatness and defect of non-linear syetem:introductory theory and examples[J].International Journal of Control,1995,61(6):1327-1360.

[5] Gensior A,Woywode O,Rudolph J.On differential flatness,trajectory planning,observers and stabilization for DC-DC converter.IEEE Trans.on Circuits and System-I:Regular Paper,2006,53(9):922-937.

[6] Shahin A,Hinaje M,Martin,et al.High voltage ratio DC-DC converter for fuel-cell applications[J].IEEE Trans.On Industrial Electronics,2010,57(12):3944-3955.

[7] Payman A,Pierfederici S,Davat B,et al.An adapted control strategy to minimize DC-Bus capacitors of a parallel fuel cell/ultracapacitor hybrid system[J].IEEE Trans.on Power Electronics,2011,26(12):3843-3852.

[8] 张军明，张弘强，杜韦静.级联高频变换系统的大信号稳定性研究[J].电力电子技术，2014,48(6):22-25.

A Constant Power Supply with Power Adjustable Characteristic

WU Gao-yang，LU Gang，WANG Hong-bo，WEI Xi

(School of Electrical Engineering,Guangxi University,Nanning 530004,China)

Constant power supply is a special power supply because of its constant power output characteristic.The traditional constant power supply has the problems of poor performance,low rate of equipment utilization and low efficiency.The research shows that the Boost converter with constant power output is a differential flatness system.The feedback system designed based on the theory of differential flatness is a effective way in transforming nonlinear systems into linear systems.It is easy to design a control system,and has a good dynamic performance and static index.In this paper,the boost converter as an example,the control strategy is designed based on the theory of Differential Flatness.Finally,a 300W Boost PFC power supply prototype is developed,which meets the design requirements and has good steady and dynamic performance.The feasibility and correctness of control strategy were verified by the experimental results.

differential flatness;constant power supply;boost converter;control strategy

1004-289X(2017)01-0016-04

广西自然科学基金(2014GXNSFAA118380)

TM91

B

2015-11-29

吴高阳(1991-)，女，安徽安庆人，硕士研究生，主要研究方向为电力电子控制与建模; 鲁刚(1990-)，男，陕西榆林人，硕士研究生，主要研究方向为电力电子技术与电源系统。