基于Ito随机微分方程大坝实时性态预测方法
2017-07-31郭岩虎
郭岩虎
(昌吉州水利局重点水利工程建设管理处,新疆 昌吉831100)
基于Ito随机微分方程大坝实时性态预测方法
郭岩虎
(昌吉州水利局重点水利工程建设管理处,新疆 昌吉831100)
针对大坝实时性态预测方法精度,首先基于Ito随机微分方程对某坝的多年扬压力监测极值建立GM(1,1)了实测序列预测模型,并根据建立模型的残差序列构建了Markov残差模型,其次对比分析了GM(1,1)残差预测模型和Markov残差模型。最后,综合GM(1,1)模型和Markov残差模型建立灰色Markov模型,并利用灰色Markov模型预测扬压力的极大值。计算结果表明,建立的灰色Markov模型不仅能提高预报精度还能真实地反映其过程的摆动性。
Ito随机微分方程;灰色Markov模型;残差辨识;关联度;预报精度
Ito方程作为一种研究随机过程的重要方法,涉及了众多领域。其方程的解过程是Markov过程。在大坝安全监测领域,根据其建立的数学模型,不仅能提高预报精度还能真实地反映其过程的摆动性。在进行大坝安全监测资料分析时,传统的数学模型缺失残差分析,如文献[2]采用混沌学构建的预报模型,文献[3]构建的统计、确定性及混合模型对大坝的安全评价。这些传统模型的不仅预报精度不高还不能真实地反映其过程的摆动性。有关学者通过构建残差模型预测大坝安全度。但残差值存在一定缺陷,并不是所有的值都是正值,也没有逐渐递增的趋势,综上,构建的传统残差模型辨识残差序列并不恰当。基于此,基于Ito随机微分方程对某坝的多年扬压力监测极值建立GM(1,1)了实测序列预测模型,并引入Markov模型对残差进行辨识。计算结果表明,建立的灰色Markov模型不仅能提高预报精度还能真实地反映其过程的摆动性。
1 模型简介
1.1 Ito随机微分方程[4]
设随机过程x={x(t),t≥0}满足如下Ito积分:
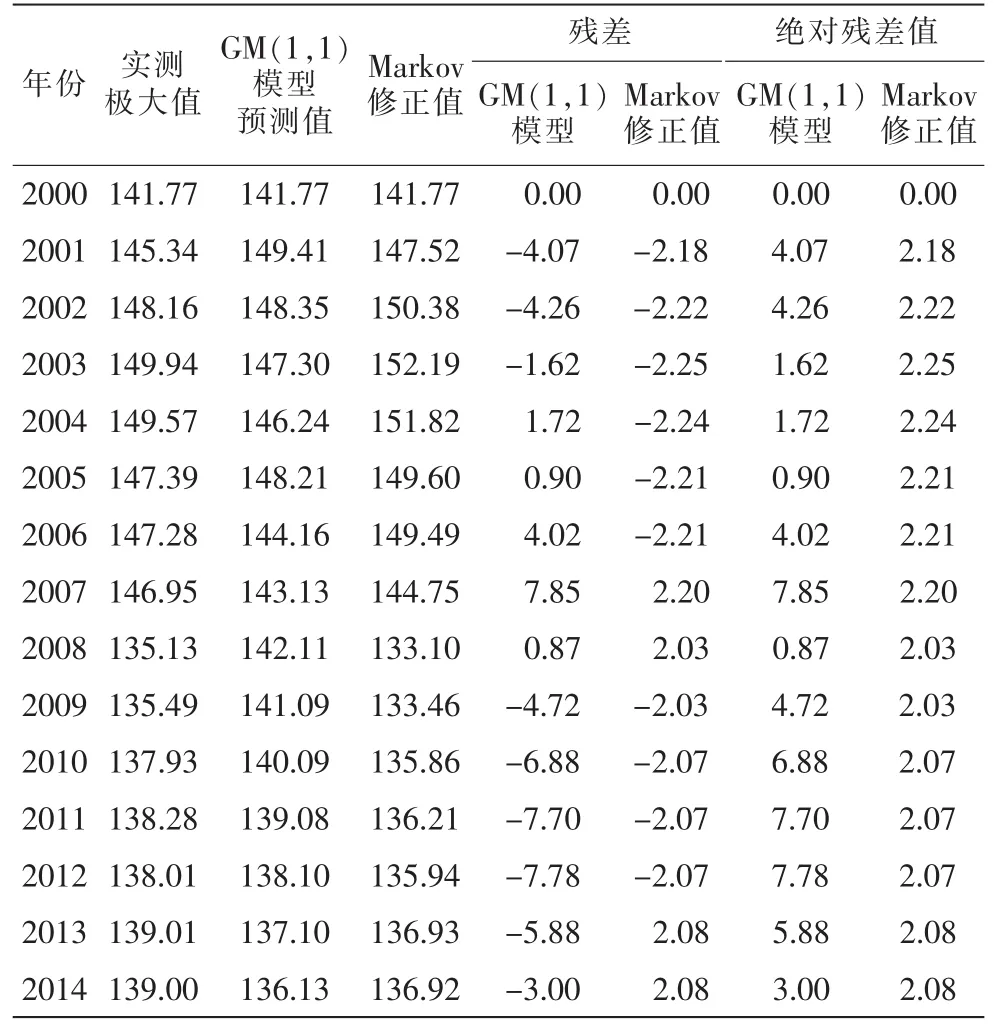
对存在t0和t在区间0≤t0 或等价地写作Ito微分的形式 式中 b(t,x),σ(t,x),为二元连续函数,对存在x属于R,且存在和σ(t)都属于,当同时满足两x(s))ds是一般的均方积分,而个条件时,则称x为Ito过程。 式(1)被称为Ito随机积分方程,式(2)被称为Ito随机微分方程。在Ito随机过程的定义式(1)中,则是Ito积分。 相关学者研究表明,对于更广义上的一般随机微分方程,不仅能够确保方程解的存在性和唯一性,还能进一步找到其渐进解。 1.2 构建灰色Markov数学预报模型 1.2.1 常规数学预报模型计算步骤 1.2.1.1 确定构建模型类型 假定原始数据为x(0)(k)(k=1,2,…,n);累加数据为模型为: 式中 a,b分别为构建模型求得的参数。 首先建立数据矩阵、数据向量,然后作最小二乘计算,则模型参数为: 最终解微分方程得到的响应函数为: 1.2.1.2 残差辨识 为提高预测数据序列及大坝原监测数据序列的关联度,需进行残差辨识: 式中 ε(0)(l)为第l时刻的残差;x(1)(l)为原数据的累加值;(l)为预测值的累加值。 1.2.2 残差辨识的Markov改进 1.2.2.1 Markov过程的基本原理 Markov过程是指某过程只与t0时刻的状态有关,与其他时刻状态无关。时间与状态为离散情况Markov过程被称之为Markov链[4]。 在大坝安全监测资料中,测点的监测物理量大小是典型的Markov随机过程,其时间与状态均为离散情况,属于Markov链。 1.2.2.2 Markov过程 大坝监测资料长序列数据中,设大坝的扬压力值H,则H∈(Hmin,Hmax),令ΔH=Hmax-Hmin,为建立一一对应的时间、空间状态模型,需将状态空间区间进行离散化,则: 式中 n为区间个数,n=0,1,2,…;h为离散后的子空间。 将长序列数据离散化后,用H1,H2,…,Hn表示,按时序将转移时间取为t1,t2,…,tn,则表示数列由状态Hi经过k步变为Hj的概率。将以往资料的出现频率作为概率的近似值: 从而可得k步状态转移矩阵为: 在确定k时,一般需考察一步转移概率。设预测状态为Hm状态,则考察R(1)中的第m行若,则可认为下一时刻最有可能由Hm状态转向Hn状态。若矩阵R(1)中的第m行有多个概率相似或一致,状态的未来转向便很难确定。这就需要考察二步R(2)或者二步以上R(k)(k≥3)的转移概率矩阵[5]。 接下来求得转向下一时段状态的概率,并确定其修正值,最后将修正值加上原预测值,便可得到Markov修正的灰色预测值[5]。 依托某水电站大坝3#坝段2000~2014年V3-1测点各年的15组扬压力极大值为例,构建其长序列G(1,1)数学模型,对预报残差进行残差辨识,对比分析常规灰色模型与改进灰色Markov模型,原数据为: x(0)=[x0(1),x(0)(2),…,x(0)(15)]=[134.12,131.13,…,122.98] x(1)=[x(1)(1),x(1)(2), … ,x(1)(15)] =[134.12,265.25,…,1968.35] 根据上述数据构建GM(1,1)模型,可得: 由此得出离散响应为: 计算结果如表1。由表1可知,扬压力极大值的残差序列有正有负,且累加值也并未出现递增趋势,模型的精度较低,且未体现其摆动性。即不能建立常规的残差模型。为体现常规残差模型性质,需对原始监测数据其加以修正。且数据的相对残差在(-5.67%,5.34%)之间。 表1 实测值与预测值及残差统计 单位:m 由Markov链基本原理可知,预报精度是由数据极大值相对残差决定,数据相对残差区间离散化程度越高,则大坝安全监测资料的预报精度相对越高。将相对残差区间离散化为4个独立的状态区间[6],4种状态分别代表灰色预测的相对残差,如表2,表3。 先由2000~2014年V3-1测点各年的15组扬压力极大值在状态区间出现的频率,结合式(9)求出近似转移概率,最后求得残差的步转移概率矩阵: 表2 状态区间划分 由表3可知,2000~2003年扬压力极大值属于状态Ⅲ,设初始矩阵[0,0,1,0],从而可通过R(1)确定下一年所属状态,以此类推,可得出之后各年所属的状态。设转移概率为P的相对残差的区间为[⊗i,⊗j],则Markov修正值[7]为: 表3 数据相对残差状态 式中 maxk(k=1,2,3,…)为不同年份的扬压力极大值。 所得修正值如表4。由表4看出:①残差序列的精度有大幅提高。与灰色预测数据叠加处理,可得Markov修正值。②运用Markov数学模型进行修正,绝对残差降低幅度明显。最后得出,预测数据关联度从数学模型的0.5525提高到了Markov数学模型修正值的0.6708。 表4 预测结果统计 单位:m (1)局部线性化Markov链模型分段线性逼近算法,计算结果验证了改进算法的有效性和实用性。 (2)将Markov随机过程建立的Markov预测模型应用于灰色预测模型的残差辨识过程中,解决了常规的残差模型的有正有负及没有递增趋势的缺点,提高了预报精度。 (3)在求得转移概率时,有效数据资料越多,即残差序列的样本容量越大,预报精度越高。 (4)由于Markov预测对监测数据要求较高,考虑到大坝建成初期的监测数据波动性较大,应删除。 [1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003. [2]包腾飞,吴中如,顾冲时.基于统计模型与混沌理论的大坝安全监测混合预测模型[J].河海大学学报(自然科学版),2003(5):534-538. [3]苏怀智,吴中如,戴会超.初探大坝安全智能融合监控体系[J].水力发电学报,2005(1):122-126,52. [4]张炳根,赵玉芝.科学与工程中的随机微分方程[M].北京:海洋出版社,1980. [5]张鑫,任永泰,王福林,等.基于改进灰色马尔科夫模型的年降水量预测[J].数学的实践与认识,2011(11):51-57. [6]董胜,刘德辅.年极值水位的灰色马尔科夫预报模型[J].水利学报,1999(1):61-65. [7]黄传胜,张家生.深基坑开挖变形的灰色马尔科夫链预测方法[J].铁道科学与工程学报,2011(2):71-75. (责任编辑:王艳肖) A real-time state prediction method of dam based on Ito stochastic differential equation GUO Yan-hu Aiming at the problem of accuracy of real time state prediction method.First of all, based on the Ito stochastic differential equation, the GM (1,1) prediction model is established for monitoring the extreme pressure of a dam, and the Markov residual model is constructed according to the residual sequence.Secondly, the GM (1,1) residual prediction model and Markov residual model are compared and analyzed.Finally, the GM (1,1) model and the Markov residual model are used to establish the grey Markov model,and the maximum value of the uplift pressure is predicted by using the grey Markov model.The results show that the grey Markov model can not only improve the prediction accuracy,but also truly reflect the swing of the process. Ito stochastic differential equation; grey Markov model; residual identification; correlation degree; prediction accuracy TV698.1 B 1672-9900(2017)03-0091-04 2017-03-14 郭岩虎(1974-),男(汉族),新疆昌吉人,工程师,主要从事工程管理方面工作,(Tel)13899677308。
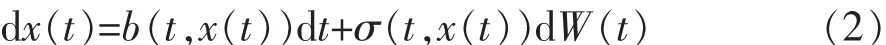

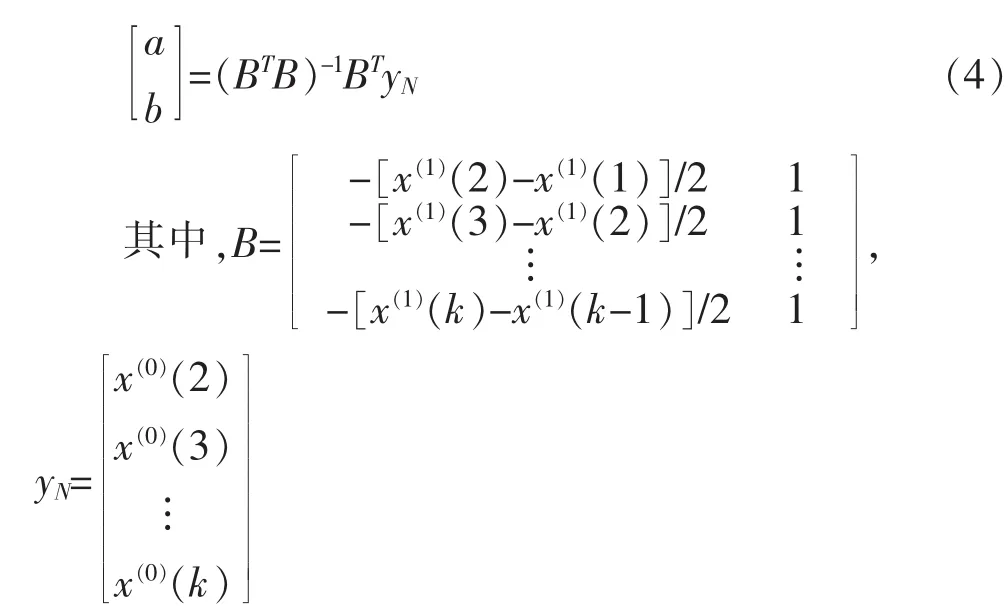

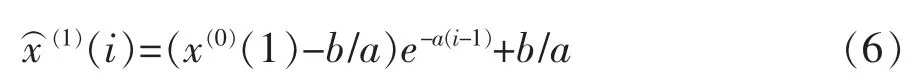




2 实例分析
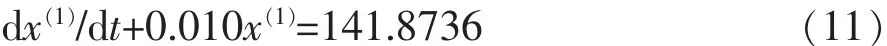
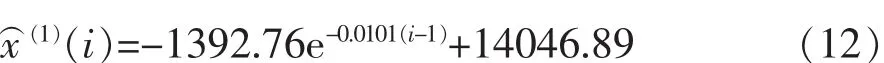




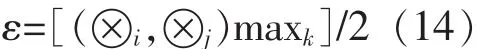
3 结语
(Changji Water Conservancy Bureau Key Water Conservancy Project Construction Administrative Office, Changji 831100,China)
