推理公式法在山区洪水变化规律分析中的应用

许 强

（新疆塔里木河流域巴音郭楞管理局，新疆 焉耆841100）

推理公式法在山区洪水变化规律分析中的应用

许 强

（新疆塔里木河流域巴音郭楞管理局，新疆 焉耆841100）

为了分析某流域内洪水产流参数和汇流参数的变化规律，在无实测水文资料的流域基础上选取了上游和下游2个控制断面，并采用推理公式法计算了不同频率下的设计洪峰流量和对应的洪水过程线，之后通过计算设计暴雨来推求设计洪水。结果发现汇流参数随着流域特征因素的增大而增大，产流参数则流域特征因素的增大而减小，汇流参数与汇流时间、设计洪峰流量呈正相关关系。研究成果可为无实测资料流域的防洪预警提供一定的计算依据。

流域；推理公式法；设计暴雨；汇流

无资料地区小流域设计洪水的推求一直是涉水工程设计当中的一个难点，而设计洪水的计算成果往往决定着工程的防洪安全和投资规模。我国幅员辽阔，山区河流众多，并且大多数河流上缺乏充足的水文站，导致较多河流缺乏暴雨洪水资料，尤其是小流域。而缺乏暴雨洪水资料的小流域，往往易发生重大山洪灾害，诱发滑坡、泥石流、崩塌等一系列地质灾害，对人民的生命和财产造成巨大威胁。因此，迫切需要对山区沿河村落进行防洪能力计算，尽量避免暴雨洪水灾害，从而减少人民生命财产的损失。

通常情况下，可以根据流量资料和暴雨资料来推求设计洪水，但对于无实测水文资料的中小流域，一般通过推求设计暴雨，进而求得设计洪水［1］。国内外对无实测资料的中小流域进行设计洪水计算研究已有多年历史，常用的小流域暴雨洪水计算方法有：推理公式法、经验公式法、综合单位线法、水文模型法等。岳华等［2］采用美国推理公式和“中铁法”对无实测水文资料的流域进行设计洪水计算，结果发现“中铁法”的计算精度更高。邵丽萍等［3］采用传统矩法、地区综合法、L-矩法来计算不同频率下小流域的设计暴雨及暴雨过程线，结果表明地区综合法和L-矩法都可应用于不同资料情况下的设计暴雨计算。王维新等［4］根据特小流域雨洪特性，应用推理公式的基本原理探讨了下垫面对洪水参数的影响及其变化规律。

本文的研究对象为山区河流，而推理公式法结合了流域产汇流条件及流域有降雨特性，所以推理公式法能更好地反映小流域的产流特性，其成果较水文比拟法具有更加良好的可靠性，且从工程安全角度考虑，确定本案例采用推理公式法进行计算。本文主要采用推理公式法计算2个控制断面处的设计洪水，并分析上下游洪水参数的变化规律，以及产汇流参数对设计洪水的影响。

1 推理公式法简介

推理公式法是一种利用暴雨资料来间接推求设计洪峰流量的简化计算方法，又称为“合理化”方法。推理公式法是在假定流域上降雨与损失均匀的基础上，即假定降雨强度在流域汇流时间t内，在时间和空间上的分布是均匀的，假定径流系数在流域汇流时间t内，在时间和空间上的分布是均匀的，然后根据流域线性汇流原理求得控制断面处的设计洪峰流量［5-6］。这些假定都是建立在流域面积不能太大的基础上，文康教授认为：在我国推理公式法最好用于300km2以下流域。推理公式法的基本公式如式（1）～式（6）。

式中 Qm为最大流量（m3/s）；ψ为洪峰径流系数；Sp为暴雨雨力（mm/h）；τ为流域汇流时间（h）；τc为产流历时（h）；n为暴雨公式指数；F为流域面积（km2）；L为自出口断面沿主河道至分水岭的河流长度（km）；J为沿L的河道平均坡度；τ0为当ψ=1的流域汇流时间（h）；μ为产流参数，即产流历时内流域平均入渗强度（mm/h）；m为汇流参数。

产流参数μ，汇流参数m都是推理公式中的主要影响参数［7］。产流参数μ基本上代表了地表平均入渗能力，影响产流参数的因素主要包括流域的下垫面条件、暴雨量大小、暴雨历时长短、暴雨时程分配及前期雨量；汇流参数m是反映洪水汇集特性的参数，影响其的主要因素包括流域所在位置的地理环境、下垫面条件、暴雨参数。产、汇流计算的精度直接影响着整个流域的洪水计算精度，其不仅受到暴雨时空分布的影响，还受到流域下垫面条件的约束。本文采用m～θ关系求得汇流参数，产流参数根据设计暴雨资料求得。

2 暴雨洪水计算

2.1 计算参数

在当地无实测的水文资料的基础上，选取了上、下游2个控制断面，分别命名为A村和B村。研究河流的流域面积149.95km2，河道全长23.8km，流向自西南向东北。在地形图上读出所选取控制断面以上的集水面积、河长，并采用加权平均法计算出河道的平均比降，最终控制断面基础参数如表1。

表1 控制断面基础参数

2.2 设计暴雨计算

根据收集到的当地水文气象资料，利用SURFER软件绘制暴雨统计参数等值线图。根据绘制暴雨统计参数等值线图，查取2个控制断面以上流域重心处10min、1h、6h、24h暴雨均值，变差系数Cv，且离差系数Cs=3.5Cv，并且采用P-Ⅲ型曲线获得P=1%、P=2%、P=5%、P=10%、P=20%的模比系数Kp值。则控制断面处暴雨参数如表2，模比系数Kp值如表3。

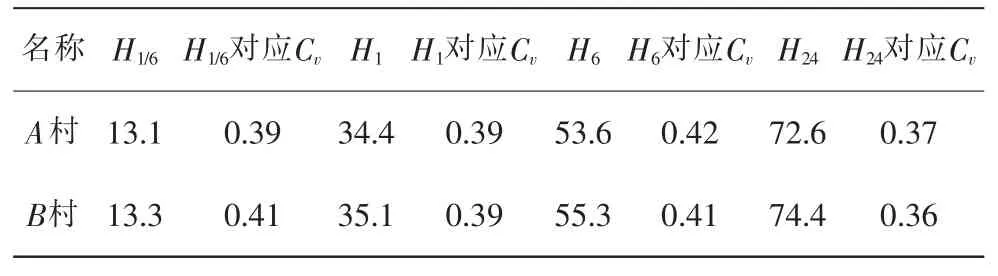
表2 控制断面暴雨参数

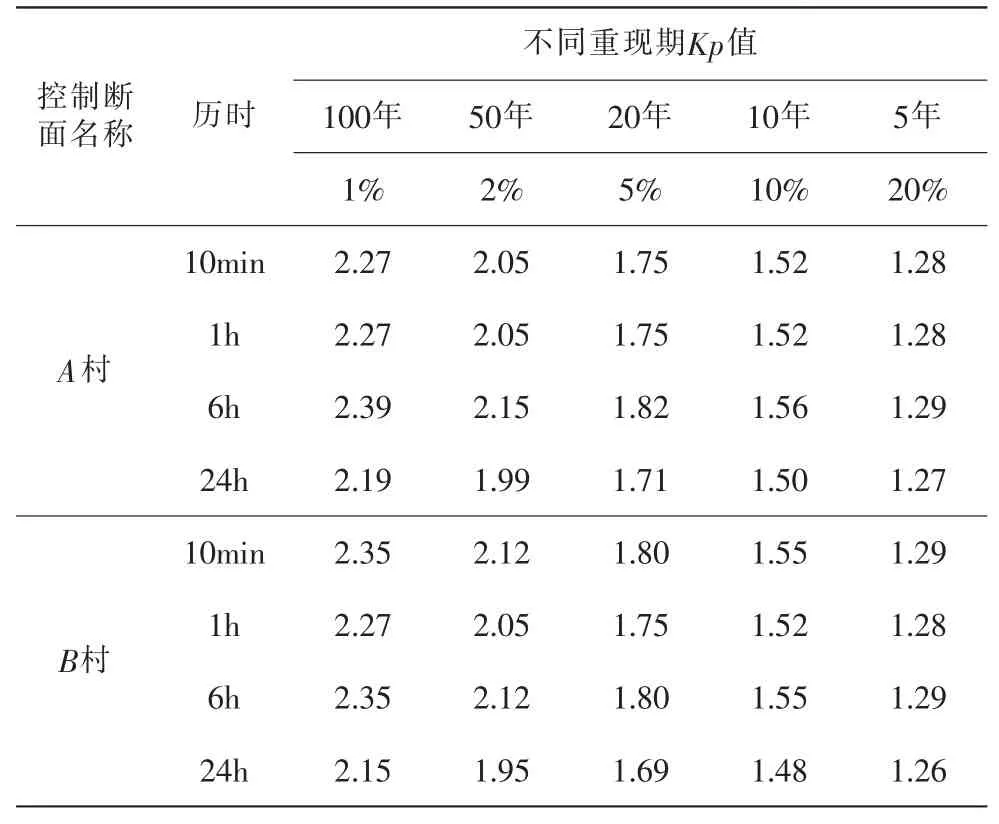
表3 控制断面处P－Ⅲ型曲线模比系数Kp值

由暴雨计算公式，计算出不同频率下的设计暴雨，如式（7）：

式中 Htp为历时t、设计暴雨频率p的暴雨量；Kp为皮尔逊Ⅲ型曲线模比系数；p为设计暴雨频率，本次计算取1%，2%，5%，10%，20%；为典型时段暴雨均值，t为设计暴雨历时，本次取10min、1h、6h和24h。

再根据《小流域暴雨洪水计算手册》查得流域面深折减系数分区为Ⅵ区，查出6h和24h面深折减系数α，则控制断面处暴雨计算结果如表4。

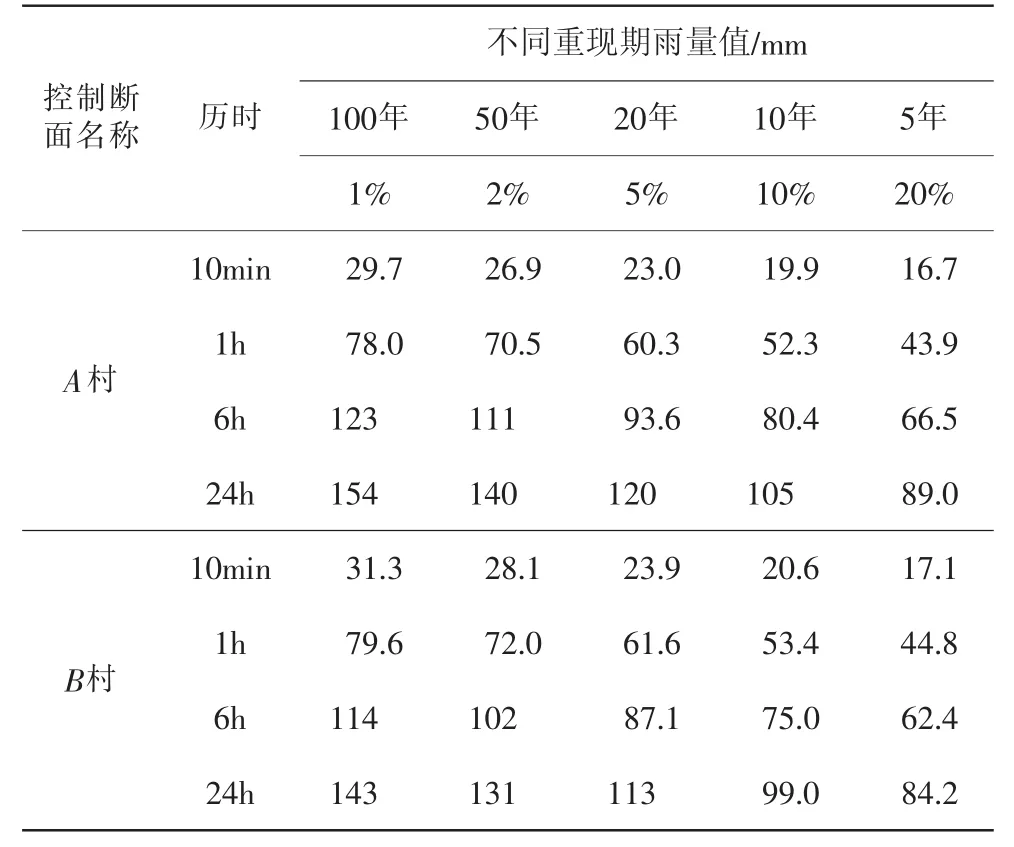
表4 控制断面处暴雨成果

2.3 设计洪峰流量计算

运用推理公式法计算设计洪峰流量，根据流域的m～θ关系，求出相应控制断面处的汇流参数m，由流域特征因素求出2个断面处的θ值，结合流域下垫面条件，选取产汇流参数，产流参数μ、汇流参数m地区类型分别取Ⅰ、Ⅱ区，则m＝0.318θ0.204，则林丰村断面处的流域特征因素θ=10.653，汇流参数m=0.515；新村断面处的流域特征因素θ=16.558，汇流参数m=0.564。再通过excel编程进行迭代计算，得出2个控制断面的洪峰流量，并根据对汇流参数进行校核。最终得到控制断面处洪峰流量计算成果如表5。

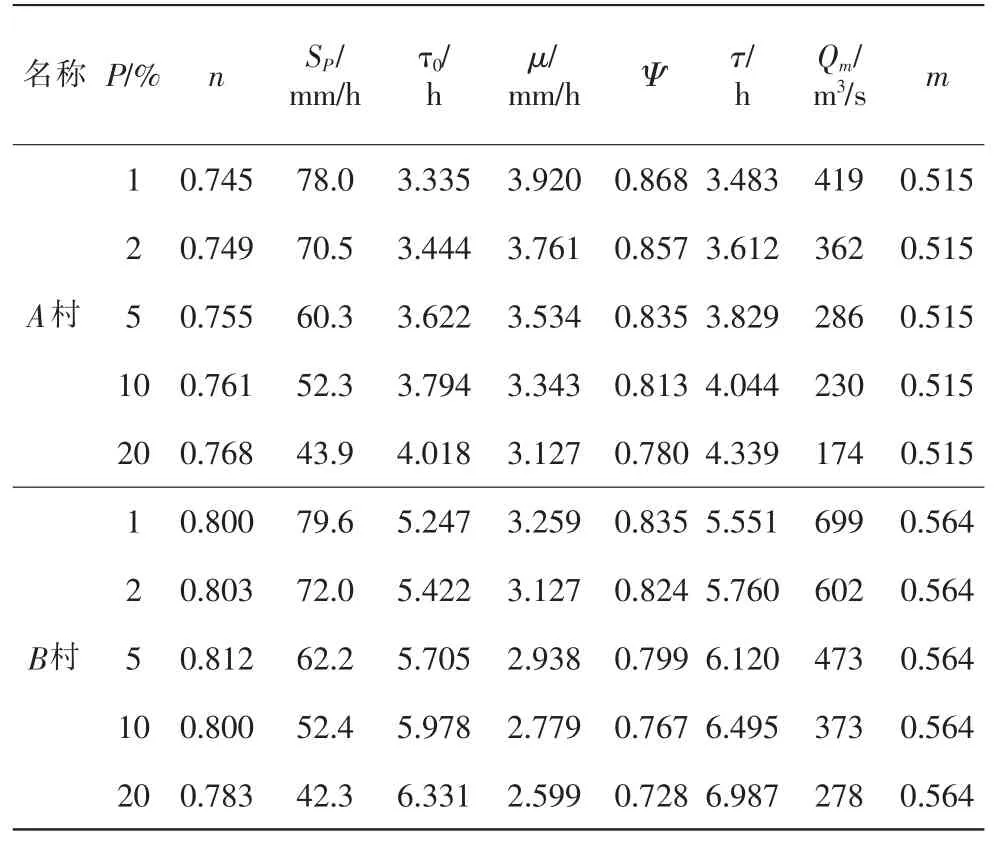
表5 控制断面处设计洪峰流量计算成果

分析以上计算结果可以看出：校核后的汇流参数与利用m～θ关系求得的汇流参数相同，则说明计算过程是正确的；Sp随着重现期的增大而增大；在同一流域上，汇流参数m随着流域特征参数θ的增大而增大，产流参数随着θ增大而减小，也就是说从上游到下游，产流参数随着集雨面积的的增大而减小，汇流参数随着集雨面积的增大而增大，即汇流时间随着集雨面积的增大而增大；汇流参数与汇流时间和设计洪峰流量成正比关系；在同一重现期，设计洪峰流量从上游往下游依次增大；对于同一控制断面，设计洪峰流量随着重现期的增大而增大。

2.4 设计洪水总量计算

由控制断面以上流域面积的大小，确定相应的设计暴雨历时。根据T=12.8F1/4算出单峰洪水的暴雨历时，当算出的T>24h，则应将单位换算为以日计，并按下式计算设计暴雨。

式中 HTP为历时为T日的设计暴雨量（mm）；H24p为年最大24h的设计暴雨量（mm）；T为设计暴雨的历时（d）；mP为暴雨公式的指数；a，b为计算mP的参数。

根据设计暴雨量求得控制断面处的设计洪水总量，并按综合分区的暴雨径流关系求得。

式中 Wp为设计洪水总量（万m3）；HTP为历时为T的设计暴雨（mm）；F为设计流域面积（km2）；α为径流系数；h为径流深（mm）。

最终控制断面处设计洪水总量计算成果如表6。

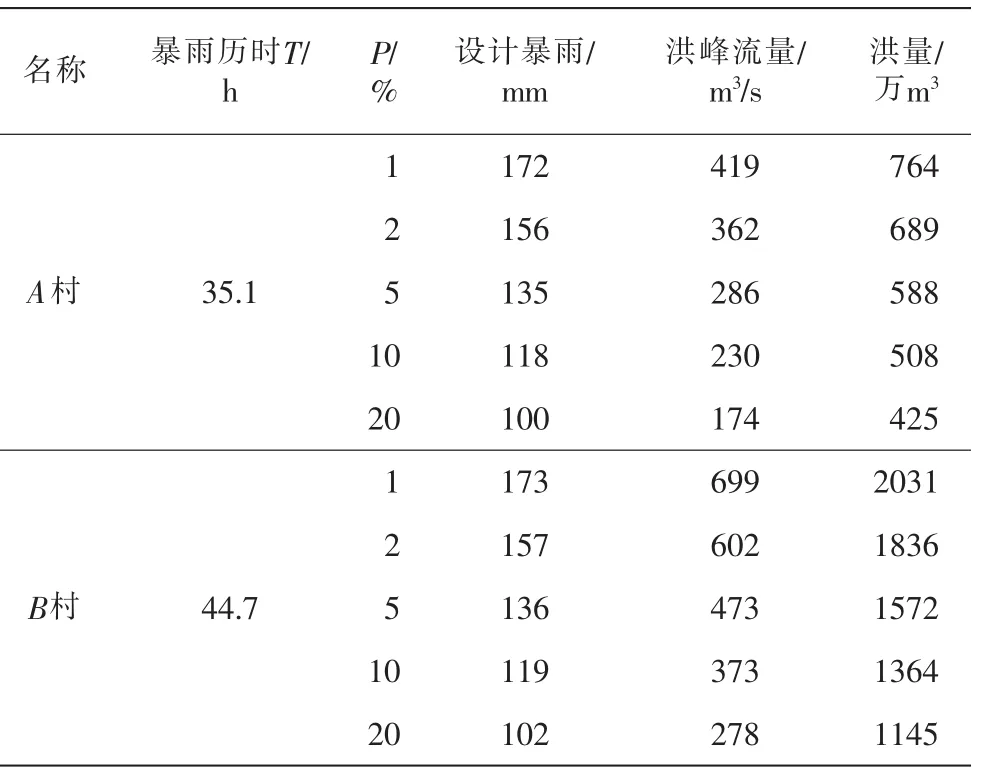
表6 控制断面处设计洪水总量计算成果

最后，根据设计洪峰流量和设计洪水总量，采用五点概化过程推求设计洪水过程线，由公式分别计算出2个控制断面处的洪水历时。则不同控制断面处不同频率下的设计洪水过程线如图1～图2。由图1～图2可以看出，重现期越大，越早达到洪峰流量，且洪水消退时间越短。

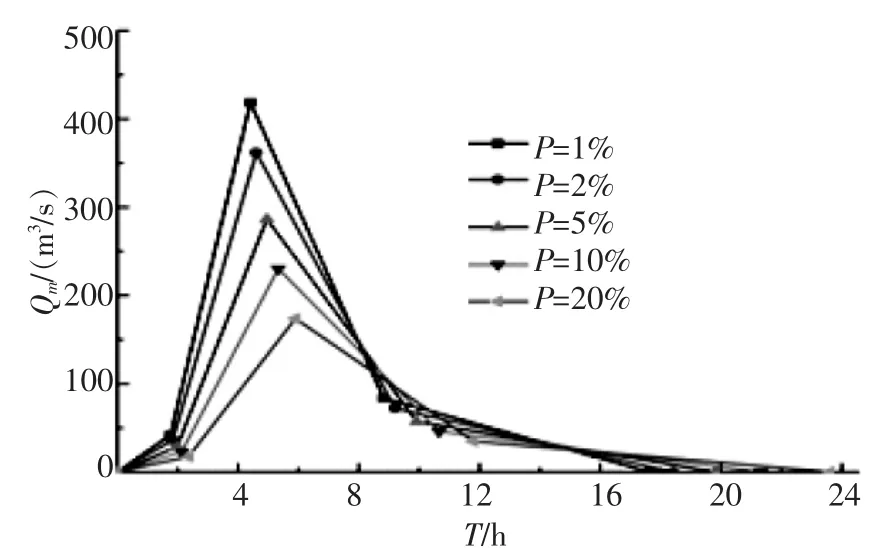
图1 A村不同频率下洪水过程线

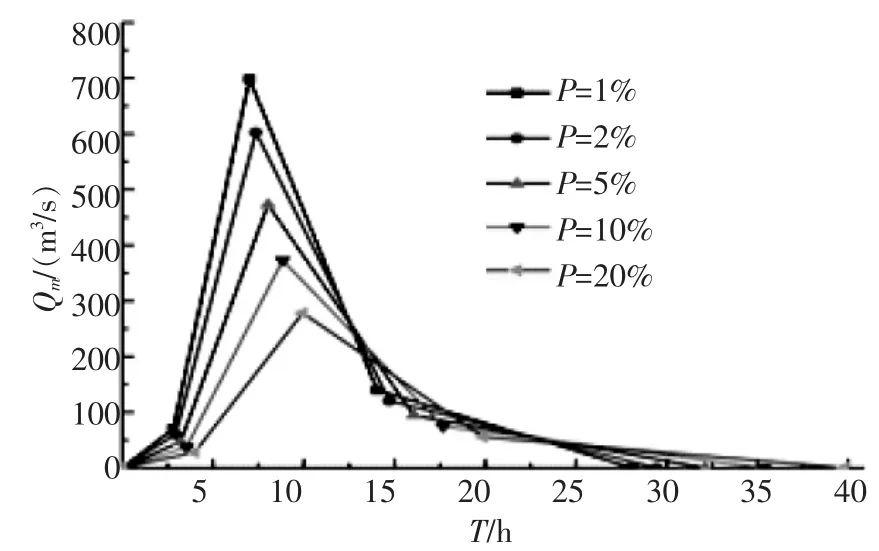
图2 B村不同频率下洪水过程线

3 结语

基于推理公式法基本理论，计算了某无实测水文资料流域上不同控制断面和不同重现期下的设计暴雨、设计洪峰流量、设计洪水总量，并根据五点概化过程绘制洪水过程线，同时根据m～θ参数关系，求得不同控制断面处的汇流参数，并对其进行校核，根据最终的计算设计洪水成果，可以得到以下结论：

（1）汇流参数随着流域特征因素θ增大而增大，产流参数随着θ增大而减小。

（2）汇流参数与汇流时间、洪峰流量呈正相关关系，即从上游到下游洪峰流量依次增大，汇流时间也越来越大。

（3）随着重现期增大，洪峰流量也相应增加，并且能越早的达到洪峰流量，洪水消退时间也越短。

［1］许月萍，童杨斌，楼章华.无资料小流域设计洪水不确定性研究［J］.中山大学学报，2008，47（6）：61-66.

［2］岳华，刘发明，颜真梅.用暴雨资料推求中小河流洪峰流量的方法研究［J］.四川大学学报，2012，44（4）：39-44.

［3］邵丽萍，许月萍，江锦红.无资料小流域不同暴雨频率计算方法的比较［J］.水文，2009，29（3）：37-40.

［4］王维新，周宪庄，张恭肃，等.华东地区特小流域洪水参数研究［J］.水文，1989，25（4）：1-9.

［5］吴婉玲，谢华伟，陈晓东.特小流域暴雨洪水计算研究概述［J］.浙江水利水电专科学院学报，2010，22（3）：30-33.

［6］谢平，陈广才，李德.乌鲁木齐地区小流域设计山洪推理公式的参数规律［J］.山地学报，2006，24（4）：410-415.

［7］魏永霞，王丽学.工程水文学［M］.北京：中国水利水电出版社，2005.

（责任编辑：姜彤宇）

Application of inference formula method in analysis of flood changing law in a mountainous watershed

XU Qiang
（Bayinguoleng Administration Bureau of Xinjiang Tarim River Basin， Yanqi 841100，China）

In order to analyze the variation of flood runoff parameters and confluence parameter in a watershed， this paper selected two control section on the upstream and downstream based on watershed without the observed hydrological data，and the design flood peak flow under different frequencies and the corresponding hydrograph are calculated by inference formula method，the design storm is developed for calculating design flood.The results show that the confluence parameter increases with the increase of watershed characteristics factors，runoff parameters decreases with the watershed characteristics factors increases.The convergence time，convergence parameters and design peak flow was positively correlated.The research results can provide a certain basis for the flood control early warning of watershed without the observed hydrological data.

watershed； inference formula method； design storm； confluence

TV122；P333.2

A

1672-9900（2017）03-0053-04

2017-03-16

许 强（1982-），男（汉族），新疆焉耆人，工程师，主要从事水文水资源方面的研究工作，（Tel）13309969300。