基于分块迭代法的分布式准正交空时码设计
2017-07-31梁国栋仝庆华卢玉和
梁国栋,仝庆华,卢玉和
(山西大同大学物理与电子科学学院,山西大同037009)
基于分块迭代法的分布式准正交空时码设计
梁国栋,仝庆华,卢玉和
(山西大同大学物理与电子科学学院,山西大同037009)
本文提出用分块迭代的方式构建半对称正交方阵和准正交方阵,在此基础上构建一种适用于多输入多输出(MIMO)天线系统的分布式准正交空时分组编码矩阵结构,并对传输性能进行仿真测试,验证其合理性,进一步推导出准正交分时码的信道编码矩阵,极大扩展信道容量。
空时编码;分块迭代;多输入多输出;准正交;信道编码矩阵
当代通信技术对通信质量和信道容量的要求越来越高。近年来,多输入多输出(MIMO)天线系统得到广泛应用,在不增加带宽的前提下,可以极大提高数据吞吐率和频谱效率。适用于多天线系统的编码技术常使用空时编码技术,通过空时域间的相关性,可达到或接近MIMO最大信道容量。
由于常用的正交空时分组码无法达到全分集和全速率同时实现的要求,往往造成发射端数据积压。我们提出准正交空时码的理念构建编码矩阵,但一般的构建方法局限于具体的天线约束,不能推广到N维情形。本文提出用分块迭代的思想构建正交及准正交方阵,从而提出一种适用于MIMO结构的n阶半对称准正交分组码矩阵结构,并对其系统性能进行仿真测试,验证其合理性。进一步推导出准正交码的信道编码矩阵,为以后接收译码工作做好理论铺垫。
1 应用分块迭代法设计方阵
1.1 半对称正交方阵
已知2k-2阶半对称正交方阵以及同阶矩阵,可采用分块迭代的思想[1]构建2k-1阶半对称正交方阵如下:


时,有

由于已知AHA+BBH=BHB+AAH,AHB-BAH=BHA-ABH=0,已知对于有 AHA=AAH,则有BBH=BHB,AHB=BAH可知用分块迭代法构造矩阵时,B为数量矩阵。我们得到通过公式(1)构建半对称正交方阵的通用方法,当编码矩阵的阶数为高阶时,体现出分块迭代法生成码字矩阵的快捷性。
1.2 半对称准正交方阵
用上节的方法推导出半对称准正交方阵[2]的分块迭代表现形式:
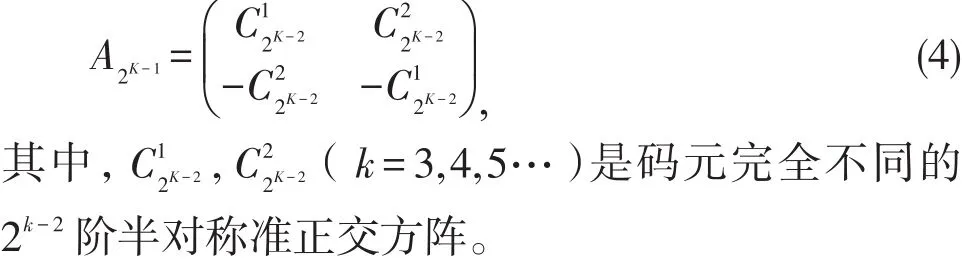
按照上述编码规则,构建4×4半对称准正交方阵如下所示:

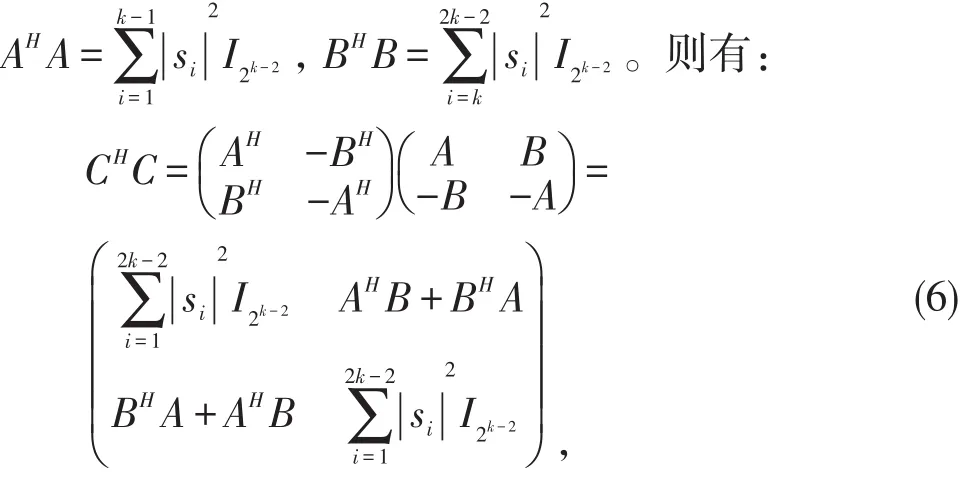
得证构造公式(4)得到的矩阵符合半对称准正交的规则。
2 准正交空时码的编码设计
假设发射天线数目为天线Mt∈N+,我们采用分块迭代法设计出一个速率为1的MIMO分布式准正交空时分组码,设计过程如下:

其中A,B由复数因子构成。
则我们可以给出向量为s1,s2的一阶半对称准正交方阵为:

我们可以推导出n阶半对称准正交空时方阵的性质如下所示:

在公式(11)和公式(12)中假设发现 A1,B1,A2,B2满足可以互换的条件,则也可实现交换。若发射端天线为Mt根,一定存在广义半对称正交方阵 Mt×Mt。
MIMO分布式准正交空时分组码方阵设计如下:
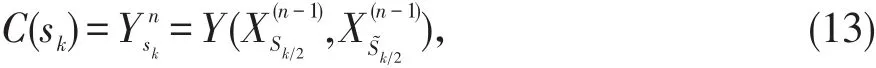
其中,Y(∙)算子的公式表示如下:

则,公式(13)可表示为:

由上式可得:

3 编码矩阵合理性分析
我们在本节以一个四阶的MIMO分布式准正交空时分组码编码矩阵来验证C(sk)满足准正交的条件。用同样的方法可以推广到n阶的情况。
设向量s=[s1s2s3s4]为码元符号向量组,由上述公式(15)给出的分布式准正交空时码构建方法,可得为:

进一步计算CHC可得:

图1给出了平坦衰落信道环境下准正交空时编码系统与最大合并比分集系统性能[4]的对比分析结果,其中接收端调制方式采用相干BPSK调制[5],信道估计为理想状态。

图1 平坦衰落信道下的准正交空时编码编码系统性能研究
由图1可知,由于分布式准正交空时编码系统的发送天线的信号功率是一发四收全分集接收系统的四分之一,所以四发一收分布式准正交空时编码的分集增益与一发四收接收最大合并比分集系统的分集增益相同,不过信噪比(SNR)相对而言丧失3 dB。若将现有的发射功率提高到原来的两倍,则系统性能趋近相同。对于四发四收分布式准正交空时编码系统和一发四收接收最大合并比分集系统可以得到相同的仿真结果。由此可知,四发一收分布式准正交空时码系统获得的分集增益与一发四收最大接收合并比系统的分集增益相同。
4 准正交空时码的信道编码矩阵
接收向量组可以表示为:R=C∙H+η,对于MI⁃MO分布式准正交空时码发射方阵C,假设传输信道为离散无记忆信道,噪声向量为η,则上式可以表示为:

根据对MIMO准正交空时码分析,可知编码矩阵决定了信道矩阵的特征,HK实际上是将准正交特性附加到初始信道参数上,给出接收向量的重排模型。下面我们给出MIMO分布式准正交空时码信道编码矩阵的具体的重排设计方法。
当发射端传输天线数Mt小于K时,则K×K的MIMO准正交空时码编码矩阵无法一次完成传输,需对整个K×K方阵每Mt列切块,按照块矩阵逐步完成发射。即原有的发射矩阵行列可等效为为K×Mt,所以对于K×Mt重构矩阵,其中可以认为重构的某些天线发射信号恒为零,即没有被使

设给定矩阵A,对于符号[A]α:β,对于几种情况的α,β值,我们分别定义如下:用。所以这部分天线对应的信道冲击响应系数为0。致使构成的整个HK中码元分布稀疏,即为一个稀疏矩阵[7]。为了推导更加简洁清晰,我们先对使用的相关符号做重新的定义。

可见HK矩阵行列为K×2K,信道矩阵HK的结构分析可以通过单根接收天线的接收情况来统一说明,我们可以定义发射端Mt根传输天线到达接收端第k根天线的信道系数向量为hk=我们同时给出推导定义如下:

则我们可以得到编码矩阵HK的内部块矩阵构造规则如下:


所以我们可以把信道接收向量公式(19)重构成下式的形式:

将上式按照相关符号的简化定义可分成上下表示如下:
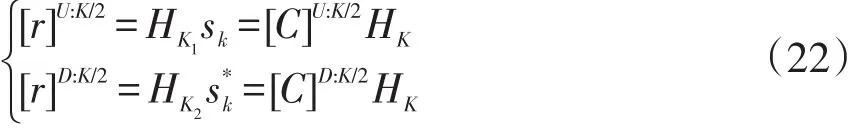
我们从MIMO分布式准正交空时编码系统的构建结构可以给出的结构。由于编码矩阵C可由半对称准正交方阵的分块迭代产生,按照上面公式(21)和(22)结构类似。且指通过向量构建的Mt阶方阵的上K 2行组成,是指通过向量构建的Mt阶方阵的上K 2行组成。
若MIMO分布式空时信道编码矩阵的特性与下式相同,即证明其体现准正交特性:
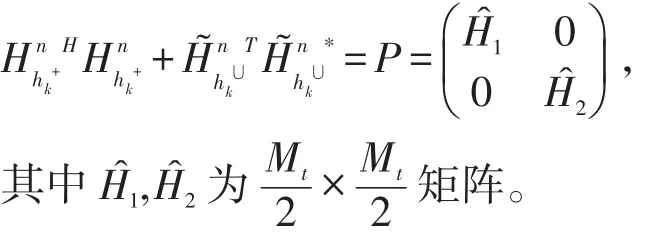
5 结束语
本文提出用分块迭代建立矩阵的方法来构建半对称的正交方阵和准正交方阵,在此基础上构建一种适用于多天线系统(MIMO)的分布式准正交空时分组码矩阵结构,使扩展后的信道编码矩阵在具备准正交特性,即发射全分集,传输全速率的特点同时可以适应多天线和多种空间信道的性能,并给出合理性分析。我们为了推导更加简洁清晰,先对使用的相关符号做重新的定义,最终给出信道编码的稀疏矩阵形式。
[1]Viterbo E,Boutros J.A universal lattice code decoder for fading channel[J].IEEE Transcation On Information Theory,1999,45:1639-1642.
[2]Jald'en J,Ottersten B.On the complexity of sphere decoding indigital communications[J].IEEE Trans on Signal Processing,2005,53(4):1474-1484.
[3]Mackay D J C,Neal Near R M.Shannon limits performance of low-density parity check codes[J].Electron Lett,1997,33:457-458.
[4]Lee J,Ryu H.A 1Gb/s flexible LDPC decoder supporting multiple code rates and block lengths[J].IEEE Trans Consumer Electron⁃ics,2008,54:417-424.
[5]Valenzuela R A.A Ray Tracing Approach for Predicting Indoor Wireless Transmission[J].Proc IEEE Vehicular Technology Conf.1993:214-218.
[6]Abdi A,Barger J A,Kaveh M.A Parametric Model for the Distribution of the Angle of Arrival and the Associated Correlation Func⁃tion and Power Spectrum at the Mobile Station[J].IEEE Trans Veh Tech,2002,51(3):425-434.
[7]Gamal El,Hammons H.A new approach to layered space-time coding and signal processing[J].IEEE Trans Inform Theory,2001,47:2321-2334.
The Design of Distributed Quasi-orthogonal Space Time Block Code Based on the Block-iterative Matrix
LIANG Guo-dong,TONG Qing-hua,LU Yu-he
(School of Physics and Electronics Science,Shanxi Datong University,Datong Shanxi,037009).
Based on the block-iterative solution to design orthogonal and quasi-orthogonal block codes,we propose an improved distributed quasi-orthogonal space time block code which does apply to multiinput-multioutput(MIMO)systems in this paper.Then we do the emulation testing for the system and the results verify that the reasonability of the design and the validity of the implementa⁃tion.So that we give the channel coding matrix further.
space time code;block-iterative solution;MIMO;quasi-orthogonal;channel coding matrix
TN919.3
A
1674-0874(2017)03-0027-04
〔责任编辑 高彩云〕
2016-12-08
山西大同大学2015年校级科研项目[2015-Q1]
梁国栋(1986-),男,山西大同人,硕士,助教,研究方向:无线移动通信。
