中国与发达国家(地区)股市间的周期相关性研究

张 瑞

(太原工业学院理学系，山西太原030008)

中国与发达国家(地区)股市间的周期相关性研究

张 瑞

(太原工业学院理学系，山西太原030008)

选取上证综指、纳斯达克指数、富时100、日经225、恒生指数分别代表中国、美国、英国、日本、中国香港股市，从频域角度研究了中国与发达国家(地区)股市间的周期相关性。结果表明：中国与美国、中国香港股市的周期相关性最强，与英国次之，与日本最弱；在长周期，中国股市滞后于中国香港、日本、英国股市，而在短周期，中国股市领先于中国香港、日本、英国股市；无论长周期还是短周期，中国股市均滞后于美国股市。

叉谱;凝聚谱;交相位谱;小波分析;股票市场;周期相关性

组合投资可通过投资不同类型的资产实现风险分散化。根据马克维茨的投资组合理论，跨国股市投资者利益取决于较低的各国股市收益相关性。然而随着全球金融市场一体化，越来越多的实证表明我国股市与国际股市的联动性在增强，投资者应注意国际风险的防范，实现最佳的投资组合策略。关于国际股市间联动现象的进一步讨论，可为组合投资者提供一定的理论参考。

对国际股市联动性的研究，可从时间序列的时域和频域两个角度分析。时域分析即直接研究时间序列随时间的变化，主要工具包括Granger因果分析、协整与向量误差修正模型等。

频域分析把时间序列视为不同频率分量的叠加，用谱来反映频域上的能量分布，为分析金融时间序列的周期相关性提供了新的视角。交叉谱作为一种频域分析工具,可用于分析不同时间序列对应频率分量间的相互关系。由交叉谱标准化而得到的凝聚谱可刻画两序列在频域上的相关性。交相位谱可进一步分析两序列在显著相关频率上的提前滞后关系[1]。李进江[2]基于交叉谱对我国上海证券市场和深圳证券市场的周期相关性进行了分析，结果表明两个市场都存在一个周期大约10个月的波动；徐颖韬[3]基于交叉谱对国际股市进行了实证研究，结果表明中国与香港、英国与美国的一致性较大；Bhandari A和Kamaiah B[4]基于交叉谱研究了BSE Sensex与其它国家股市间的周期相关性，结果表明印度与其它发达国家股市在低频段没有显著的波动关系。

由于股票市场受到各种偶然因素的影响，其指数存在噪声，影响进一步研究，故有必要进行去噪。传统的去噪方法有移动平均法、传统滤波法等。相比之下，小波变换法能更有效消除噪声，并充分保留原时间序列的特征[5]。本文将采用小波变换法进行去噪，以期得到更合理的结果。

主要目标是从频域角度分析中国与发达国家(地区)股市间的周期相关性。第一部分介绍小波变换去噪方法和交叉谱分析等理论基础。第二部分基于2012年1月4日到2017年3月9日的上证综指、纳斯达克指数、富时100、日经225和恒生指数进行实证分析。第三部分给出相应的讨论与结语。

1 理论基础

1.1 小波变换

小波(wavelet)，指小区域的波，是一种平均值为0、特殊的、长度有限的波形。小波分析是将信号分解成由一个母小波通过平移和尺度伸缩得来的小波函数的叠加。信号 f(t)的连续小波变换(continu⁃ous wavelet transform)定义为：

相应的重构公式(小波逆变换)为：

其中 f(t)∈L2,a,b∈R,a≠0,a为尺度参数,b为平移参数,Ψ(t)为母小波函数。

信号的小波系数随尺度的增大而增大，而噪声则正好相反。根据信号和噪声在不同尺度上有不同的传递特征，小波变换可实现信号的去噪。首先依次对信号和噪声的小波系数进行处理，然后通过对处理后的小波系数进行逆变换实现数据的重构，从而得到去噪后的信号[6]。

1.2 交叉谱及其估计方法

设由 Xt,Yt,t=0,±1,±2,…，构成二维平稳时间序列，则Xt与Yt的交叉谱(cross-spectrum)定义为

其中φXY(f)为交相位谱(phase spectrum)，可表示两信号在频率 f的提前滞后关系。若φXY(f)＞0，则Xt在频率 f上滞后于Yt；反之，若φXY(f)＜0，则Xt在频率 f上提前于Yt。

Xt与Yt的凝聚谱(magnitude-squared coherence)为

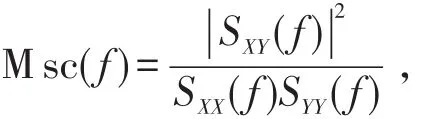
其中SXX(f)为Xt的单谱，SYY(f)为Yt的单谱。凝聚谱刻画了Xt与Yt在频域上的相关程度，取值范围为区间[0,1][1]。

Welch交叉谱估计方法的基本思想如下[7]：第一步对数据进行分段，可有重叠，总共N个，分成NB段，每段Ns个；第二步对每一段做加窗交叉谱估计，其估计式为

其中ht是长度为Ns的窗函数，Xt+l-1是该段的数据点，l是该段的起始点位置。第三步对各段交叉谱求平均[7]。

若已估计出交叉谱和单谱,可进一步根据定义估计凝聚谱和交相位谱。凝聚谱估计值通常均大于零，但并不代表在任何频率上都存在相关性，故有必要做非零相关性检验。在显著性水平α下,凝聚谱估计的临界值为1-α2/v-2，其中v为自由度。若估计值超过这一临界值,说明两序列在对应频率上显著相关[8-9]。

2 实证分析

2.1 数据及其预处理

为研究我国与发达国家(地区)股市间的周期相关性，选取上证综指(SCI)代表我国股市，另选取纳斯达克指数(IXIC)、富时 100(FTSE)、日经 225(N225)、恒生指数(HSI)分别代表美国、英国、日本、中国香港股市。选取样本时间为2012年1月4日到2017年3月9日，这是金融危机后全球经济恢复和发展的阶段。采样间隔为1天，剔除公共的非交易日(周六周日)，通过线性插值使其余数据补全并对齐，每个指数有1408个数据。数据来源为wind资讯。

鉴于金融时间序列信噪比低，采取非线性小波变换阈值法进行小波分析，小波函数选取symN5函数、阈值依据固定阈值准则(sqtwolog)选取、分解为4层。图1为对上证综指进行小波分解的结果。由于小幅波动不具有分析和预测价值，视为噪声，故去掉小的波动，保留有用信号。经分析，选择去掉如图1中d1小幅波动。去噪后，指数曲线明显平滑，噪声明显消除。另外，对纳斯达克指数、富时100、日经225、恒生指数也进行同样的去噪处理，结果从略。鉴于金融时间序列非平稳,对去噪后的股票指数零均值化，并且去趋势。接着进行ADF平稳性检验，结果显示各序列均已平稳化。

2.2 凝聚谱估计

分别对上证综指与纳斯达克指数、富时100、日经225、恒生指数进行交叉谱估计、凝聚谱估计和交相位谱估计，从而研究我国与发达国家(地区)股市在频域上的相关性，即周期相关性。考虑到尽量提高估计性能，又不会造成大量计算，影响速度，将采用Welch方法(加hanning窗，50%重叠，窗长度512)进行估计。在选择该参数的情况下，经计算，显著性水平为0.05时,临界值为0.55。即当凝聚谱估计值大于0.55时，可认为在对应频率上显著相关，存在周期相关性。图2为凝聚谱估计结果，其中横坐标为频率，纵坐标为凝聚谱估计值。

图1 对上证综指的小波分解

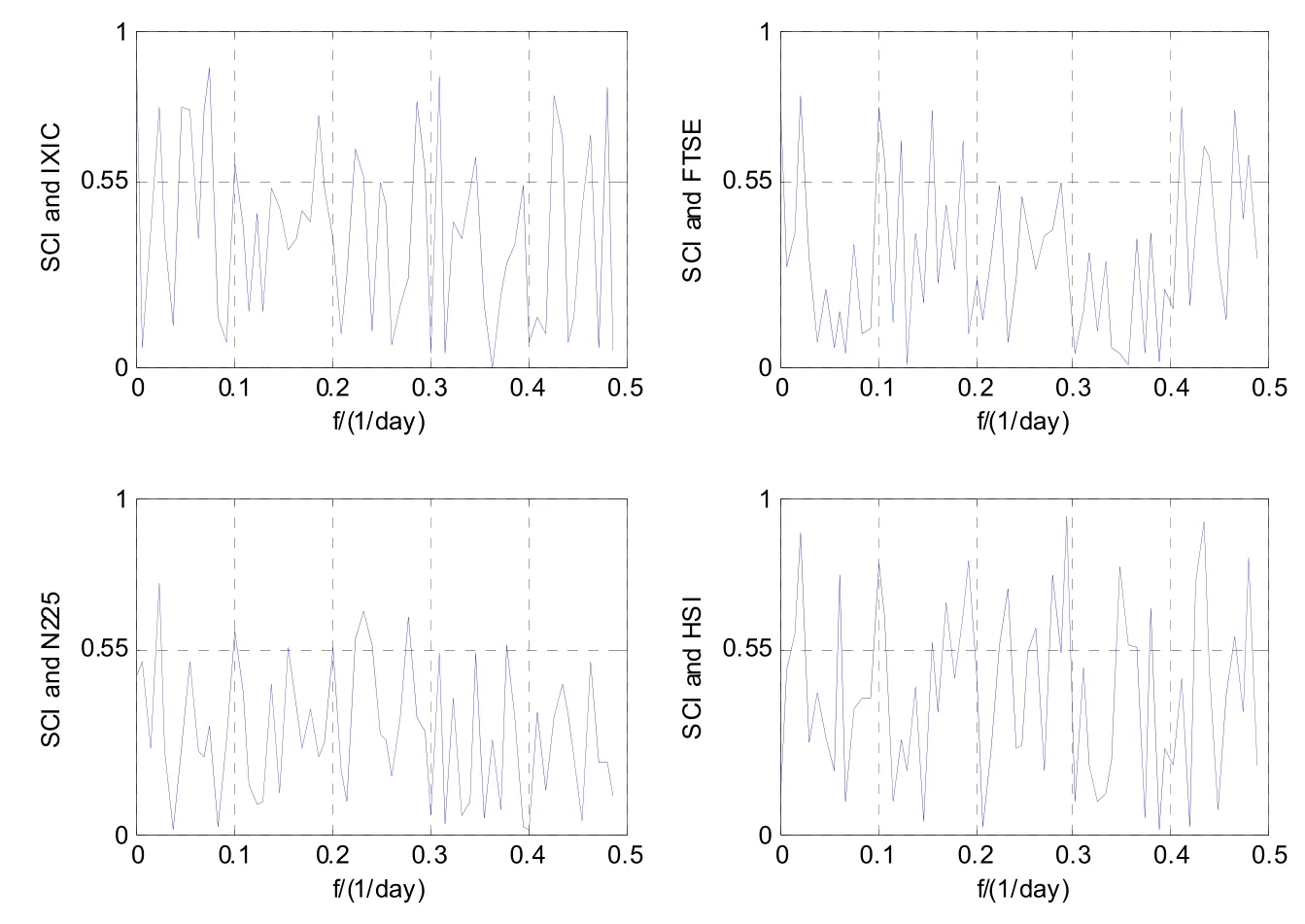
图2 凝聚谱估计结果

从图2可以看出，上证综指与恒生指数在2、3、4、5、6、17、43天存在显著相关性，对应凝聚谱估计值几乎均大于0.8，相比于其它，中国与中国香港股市间的周期相关性最强；上证综指与纳斯达克指数在2、3、4、5、21、43天存在显著相关性，对应凝聚谱估计值几乎均大于0.75，无论长周期还是短周期，中国与美国股市间的周期相关性较强；上证综指与日经225在4、10、43天存在显著相关性，凝聚谱估计值最大为0.75，随着频率的增大，显著频率变少且对应凝聚谱估计值变小，中国与日本股市间的周期相关性较弱，且在短周期上几乎不存在周期相关性；上证综指与富时100在5、6、8、10、43天存在显著相关性，凝聚谱估计值介于0.63～0.80，说明中国与英国股市间的周期相关性介于中国香港和日本股市。

为分析股市间的领先滞后关系，寻求显著频率对应的交相位谱估计值。若交相位谱估计值大于零，则认为上证综指滞后于其它指数；若交相位谱估计值小于零，则认为上证综指领先于其它指数。图3为交相位谱估计结果，其中横坐标为频率，纵坐标为交相位谱估计值。从总体上来看，在长周期，中国股市滞后于中国香港、日本、英国股市，而在短周期，中国股市领先于中国香港、日本、英国股市。无论长周期还是短周期，中国股市均滞后于美国股市。

3 讨论与结语

图3 交相位谱估计

为研究中国与发达国家(地区)股市间的周期相关性，采用Welch法对上证综指与纳斯达克指数、富时100、日经225、恒生指数进行了交叉谱估计、凝聚谱估计、交相位谱估计。结果表明：中国与美国、中国香港股市的周期相关性最强，与英国次之，与日本最弱；在长周期，中国股市滞后于中国香港、日本、英国股市，而在短周期，中国股市领先于中国香港、日本、英国股市。无论长周期还是短周期，中国股市均滞后于美国股市。

从短周期来看，各国或地区汇率等因素的不断变动会引发短期资本流动，影响股票市场，从而产生联动现象。另一方面，股市间长周期相关性充分反映了世界经济金融一体化。中国与其它各国保持密切的贸易往来，主要贸易伙伴的经济状况和宏观政策会对我国经济产生影响，同样我国也会对其它国家(地区)产生影响，宏观经济间的影响也必然会反映在股市上。仅从频域角度研究了中国与发达国家(地区)股市间的周期相关性，更多的结论需要在未来的工作中深入研究。

[1]PRIESTLEY M B.Spectral Analysis and Time Series[M].London New York:Academic Press,1981:654-726.

[2]李进江.我国股市协整检验及周期波动[J].统计与决策,2005(22):102-104.

[3]徐颖韬.国际证券市场的相关性、周期性及传导特征实证研究[D].长春:吉林大学,2008.

[4]BHANDARI A,KAMAIAH B.An Analysis of Lead-Lag Relationship between Stock Returns Using Spectral Methods[J].Social Sci⁃ence Electronic Publishing,2015,14(1):21-32.

[5]兰秋军,马超群,文凤华.金融时间序列去噪的小波变换方法[J].科技管理研究,2004,24(6):117-120.

[6]孙吉红.长时间序列聚类方法及其在股票价格中的应用研究[D].武汉：武汉大学,2011.

[7]MCKONE K P.Multiple Methods of Spectral Analysis with Applications to the Florida Current[D].Hattiesburg:University of South⁃ern Mississippi,2003.

[8]KOOPMANS L H.The Spectral Analysis of Time Series[M].New York:Academic Press,1974:281-285

[9]GALLET C,JULIEN C.The significance threshold for coherence when using the Welch’s periodogram method[J]:Effect of overlap⁃ping segments.Biomedical Signal Processing and Control,2011,6(4):405-409.

The Co-movement between China's Stock Market and Developing Countries'Stock Markets

ZHANG Rui
(School of Science,Taiyuan Institute of Technology,Taiyuan Shanxi,030008)

The Shanghai Composite Index,the Nasdaq Index,the FTSE 100,the Nikkei 225 and the Hang Seng Index respective⁃ly stand for stock markets of China,the United States,the United Kingdom,Japan and Hong Kong.This paper examines the relation⁃ship between China’s stock market and four other stock markets of developed country(area)in frequency domain.The results show that coherence between China’s stock market and other developed markets is significant.In the long run,the stock markets of Hong Kong,Japan and the UK seem to lead China.In the short run,however,the stock markets of Hong Kong,Japan,the UK lag behind China.whether the short or long run,the China’s stock market is lagging behind the US market.

cross-spectra;magnitude-squared coherence;phase spectrum;wavelet analysis;stock markck;co-movement

F114.44

A

1674-0874(2017)03-0016-04

〔责任编辑 高海〕

2017-02-15

太原工业学院青年科学基金[2017LQ07]

张瑞(1989-)，女，山西长治人，硕士，助教，研究方向：时间序列。