油液速度对悬浮流特性的影响分析

陈 彬, 刘 阁

(重庆工商大学废油资源化技术与装备工程研究中心,重庆 400067)

油液速度对悬浮流特性的影响分析

陈 彬, 刘 阁

(重庆工商大学废油资源化技术与装备工程研究中心,重庆 400067)

油液中含有颗粒物会影响设备的正常运行,考察不同初始速度条件下含颗粒油液的悬浮流中各相的动态特征,利用连续介质模型建立含悬浮颗粒油液的动力学模型,并通过特征线法进行数值求解,得到在不同初始速度条件下各相参数的变化趋势。结果表明:不同初始速度条件下管路始端、中段和终端油液的压力、流速都分别在T/4的奇数倍、整数倍、偶数倍时刻产生跃变,且它们的周期(T)都随着初始速度的增加而减小;悬浮颗粒的浓度分布与油液压力的变化趋势相反。

连续介质模型; 特征线法; 油液速度; 悬浮颗粒; 浓度分布

油液是工业重要的润滑、冷却物质以及工作介质[1],在运行过程中由于机构磨损或外部浸入等方式会在油液中出现诸如金属磨粒和胶质、氧化物等非金属颗粒,这些颗粒物的存在会给机械运动部件造成卡涩、堵塞等问题,严重影响部件的正常工作机能[2]。由于这些颗粒物的尺寸较小(一般粒径在100 μm以下),在油液中呈悬浮状态,很难利用现有的技术将其分离。含悬浮颗粒的油液是一个典型的稀疏悬浮两相输送问题,Man等[3]对水沙输送建立了基于粒子质量守恒方程和Langevin方程的随机偏微分方程组,仿真了明流中沙粒的输送过程。在模型中用迁移项和随机项来表示水流中任一粒子的迁移都作为随机扩散过程;将流速的随机公式代入对流扩散方程中获得水沙输送的随机偏微分方程组,用格子近似法求解方程组,结果表明在实验数据的验证方面所建模型结果比确定性的对流扩散模型较好。傅旭东等[4]用非弹性碰撞结合BGK模型推导了稀疏流固两相流的动力学模型,用Chapman-Enskog方法获取方程的近似解构建粒子的本构关系。盛晓飞[5]以连续介质模型为基础,建立了一个较完备的丹酚酸水提取流动扩散模型。对中药提取中两相流扩散运动进行数值模拟,分析了温度、粒径、固液比等工艺参数对提取效率的影响。李洪州等[6]用类特征线法计算了高压室含灰的无限长激波管非平衡流动解,详细分析了非平衡流场,并将冻结流解和平衡流解作详细的对比分析,清楚地显示了含灰气体激波管非平衡流动从冻结流向平衡流过渡的各种细节。Muste等[7]利用两相流和均质流两种方法研究了管路水沙输送系统,获得了悬浮沙粒沿管路径向的分布规律,沙粒与水流的湍流状态相互耦合,含沙水的流速比纯水流速低且与沙粒的密度无关,沙粒的速度滞后于5%的水流速度,并认为两相流方法研究水沙输送比用均质流方法在诠释耦合湍流结构更准确。Hsu等[8]用两相流研究了水沙悬浮稀疏流,推导了湍流能量方程的摩擦衰减项,仿真结果表明由线性曳力推导的摩擦项的应用使粒子浓度分布与实验值吻合较好。傅旭东等[9]研究了稀疏相液固两相管流的动力学理论,建立了水平方管内液固两相流的数学模型,并应用LDV技术对模型结果进行了验证。所建模型能够获取粒子浓度的垂向分布的两种形式,在管内中心区,粒子均速的模型预测值小于流体的均速,在近壁区情况则相反。Leo等[10]对泥沙流建立了数学模型,获得了粒子的浓度分布、流体速度分布和湍流衰减情况,根据实验结果75%的模型结果是在测量值的0.5～2倍。Morten等[11]研究了水平管内水中半稀疏悬浮流粒子的输送情况,应用3种不同密度的250 μm粒子(聚苯乙烯粒子、镀银聚苯乙烯粒子以及SiO2粒子),相应的浓度为0.5%、2%和5%,流体分为均匀性和非均匀性两种，测试了流体的轴向速度和湍流强度以及粒子的浓度，表明粒子的密度和雷诺数显著地影响粒子的分布,对于聚苯乙烯粒子,随着浓度的增加其湍流强度也增加,而密度较大的SiO2粒子在管路底部呈现同样的特性。笔者利用两相流的连续介质模型,构建含颗粒物油液的稀疏悬浮流动力学方程,通过数值求解,获取速度对油液、颗粒物沿管路长度的速度以及颗粒浓度分布等动态特征的影响规律。

1 含悬浮颗粒油液连续介质理论模型

假设油液与其中的颗粒物都是连续介质,两相间的作用力由于颗粒尺寸较小仅用油液的曳力表示,在统计平均意义上建立它们的基本方程。

(1)控制方程。取油液中单一相的一个微控制体Θ,设在Eular坐标下ψi是对应i相的空间坐标x以及时间t的流动参数,记为ψi=ψi(x,t),则ψi的控制方程(瞬态)可写为

(1)

式中,ψi为第i相的流动参数;i为油相(f)或颗粒污相(p);ρi为第i相的密度;vi为第i相的速度;Ji为第i相的流动参数的面通量;φi为单位质量的控制体源相。

由于含悬浮颗粒油液在管路内流动,管路的长度与直径比较大,因而将式(1)变换为一维方程组。且不考虑温度的影响,则油液的连续介质模型由各相的连续性方程和动量方程组成。在油液流动过程中,流速与压力波速相比很小,因而忽略迁移加速度项以及二次项,模型可简化为整理得

(2)

式中,c为颗粒物的浓度;uf和up分别为油液和颗粒的速度;p为油液的压力;af和ap分别为油液和颗粒的应力波速;μf为油液的动力黏度;D为管路直径。

(2)模型的特征线方程。通过特征线法,式(2)可转换为分别沿各自积分线的常微分方程组,即特征线方程与相容方程。设ufp=uf-up,λf=λ-uf,λ-up=λ-uf+ufp=λf+ufp,则特征方程为

ufp)2=0,

可得4个特征线方程为

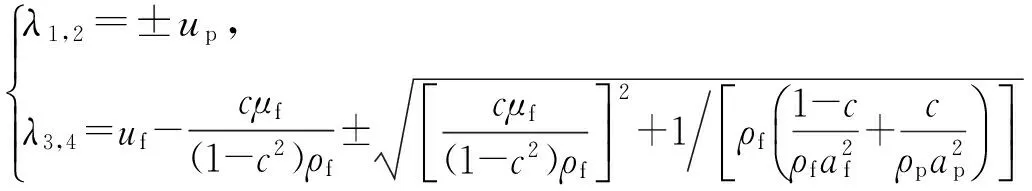
相容方程为

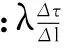
(3)

(4)

(5)

(6)

式中,上标P对应第j时刻第i管长点的物理量;上标A与D分别为油液特征线与空间坐标轴的交点第j时刻的第i-1与i+1节点对应的物理量;上标B和C分别为颗粒物特征线与空间坐标轴i-1、i+1的交点对应的物理量。

(3)初始条件与边界条件。设定含悬浮颗粒油液的初始条件:颗粒浓度(质量分数)为0.01%,速度为0.1 m/s,油液的初始压力为0.15 MPa,流速为0.1 m/s。

边界条件包含管路的始端和终端2部分,其中始端边界条件设定颗粒与油液速度相等,终端边界条件中,压力为自由边界即为大气压,在油液传输过程中,设定颗粒的数量不变,即含悬浮颗粒的油液在管路中的混合密度为定值。

2 结果分析

2.1 模型验证

根据以上建立的含悬浮颗粒油液的连续介质模型,悬浮流较为常见的是水沙两相流,Saskatchewan Research Coumcil(SRC)研究了水沙输送管路的压降与流体速度的关系,获得了一些经典实验数据,其中一组数据的实验条件为管路的直径为52.451 mm,沙水密度比为2.65,颗粒的中值为0.175 mm,颗粒的体积浓度为0.118。采用与SRC的实验数据以及Sunrata 提出了一个对悬浮流管路的全压差的模型相同的实验条件,对所建模型的有效性进行比较。结果如图1所示。

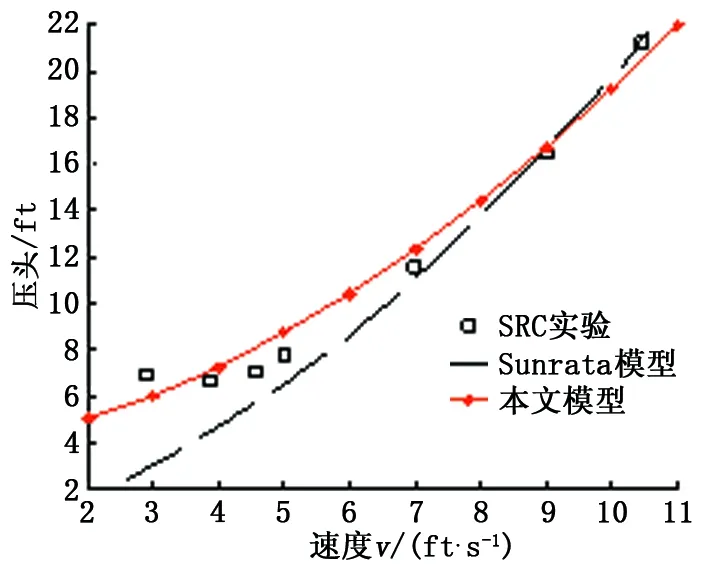
图1 模型与实验结果比较Fig.1 Comparison of models and experimental results

由图1看出,含悬浮颗粒油液的连续介质模型与SRC的实验数据的变化趋势比较一致,在流速为4～7 m/s模拟值大于实验值,可能是由于模型中对流体所受的切应力设置的数值略小的缘故,但总体上所建模型反映了管路压降的动态特征;相比Sunrata提供的模型结果,连续介质模型在流速较低的区域与实验数据的接近程度大,更能精确地描述管路压降的变化趋势。利用含悬浮颗粒油液的连续介质模型能够有效地分析油液中悬浮颗粒的动态特征,利用这个模型探讨流体速度对悬浮颗粒的影响规律是可行的。

2.2 流速对油液、悬浮颗粒的影响分析

设定含悬浮颗粒的油液管为0.044 m×0.044 m的方管,管路长度L为0.5 m,油源压力0.15 MPa,管道终端油液压力为0.1 MPa,各相的参数为:油液为25#变压器油,油液密度为895 kg/m3,油液的弹性模量为1.2 GN/m2,油液的动力黏度为1.074×10-2Pa·s,悬浮颗粒为铜颗粒,中值粒径为25 μm,浓度为0.01%,颗粒密度为7 800 kg/m3。考察油液速度在0.51～2.01 m/s变化时对含悬浮颗粒的动态影响情况。

(1)管路始端速度对油液、悬浮颗粒的影响。以最小设定速度0.51 m/s的一个循环周期T为基准,将其他速度对应的周期与T相比得到的值为横坐标,分别将压力、浓度、速度与对应的初始压力p0=0.15 MPa、初始浓度c0=0.01%以及最小设定速度v0的比值作为纵坐标,获得不同油液速度条件下油液压力、速度以及颗粒的速度、浓度的自模化变化趋势图。在管路始端不同油液速度下油液压力以及悬浮颗粒的浓度分布随时间的变化如图2所示。

最小设定速度0.51 m/s的循环周期为4L/v0=3.921 6 s。由图2(a)可见,最小设定速度0.51 m/s的速度曲线分别在在T/4、3T/4时,即T/4的奇数倍时有一个跃变,对应图2(b)中最小速度时油液压力同时产生变化。这是由于管路始端、末端存在压力差,当始端压力作用在油液中时,会产生一个向前传播的压力波,使波后的油液密度增加,压力增加,则整个管路的压力为始端压力p0,油液处于压缩状态。在末端处油液受压状态得到释放,流速增加,压力降低,产生反向传播的压力波,经过T/4时间(图2(b)中的0～T/4段)传播到管路始端,此时在始端油液速度增大,密度减小,使得压力再次降低,使始端减少的油液很快得到补充,因而油液速度很快降低到设定速度,但管内其他部分仍为较大的速度,出现速度的第一个阶跃(图2(a)中的0～T/4段);油液以v0传播到末端,由于管内压力小于末端压力,则流速降低,压力升高,压力波反向传播到管路始端。这样经过T/2时间,在管路始端管内压力小于始端压力,流速恢复到v0,出现速度的第二个阶跃(图2(a)中的T/4～3T/4段);压力再次升高(图2(b)中的T/4-3T/4段),完成一个循环。

在图2(a)、(b)中不同速度条件下油液的流速、压力的变化趋势都和最小速度情况一致,只是它们的变化周期不同。可以看出初始速度越大,油液的流速、压力的变化周期越小。在图2(c)中颗粒浓度的变化规律与油液压力完全相反,因为油液压力由高到低变化时,会使颗粒受压缩状态得以缓解,从而使其浓度升高,反之亦然。不同流速情况下,颗粒浓度的变化频率不同,从而说明了油液中颗粒的浓度与压力变化密切相关。

图2(d)表示颗粒的速度与设定始端速度一致,不随着时间发生变化,与油液流速、压力的变化规律迥然不同。

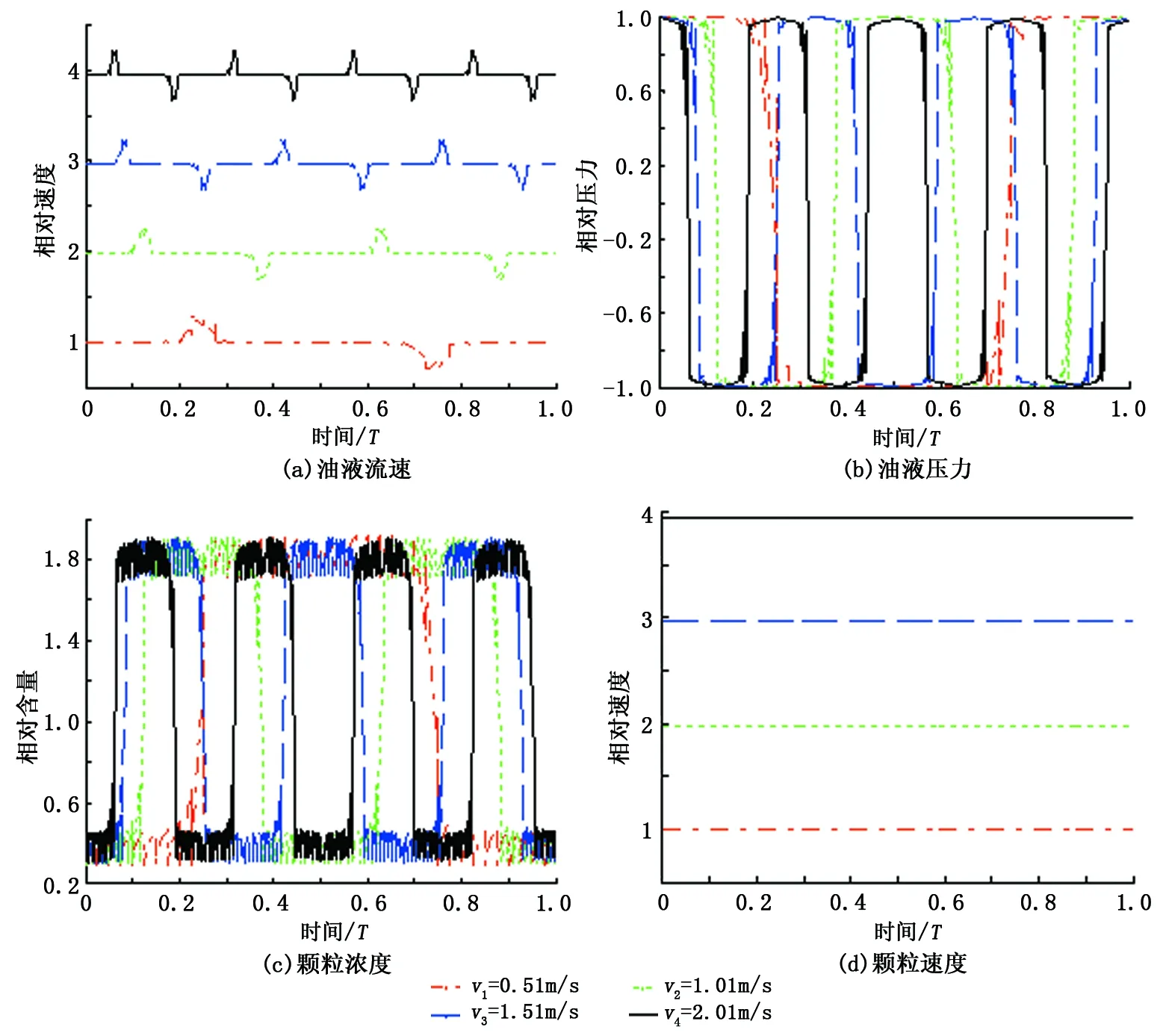
图2 管路始端各相参量的变化规律Fig.2 Variation of phase parameters in beginning of pipeline

(2)管路中段速度对油液、悬浮颗粒的影响。图3为管路中段参数变化情况。由图3(a)看出,管路中段流速的脉动规律性较强,图3比图2(a)提前T/8时间进行变化。在T/8时刻第一次反向压力波由管路末端到达中段时,速度增加,密度减小,压力下降(图3(b)),直至压力波到达管路始端,然后初速、更小的压力正向传播到中段,压力、流速出现下降跃变,经过T/4时间一直保持到反向的更小流速以及增加的压力到来,从而完成一个循环周期。随着初始速度的增加,油液的压力、速度变化的周期减小,但它们的变化趋势一致。

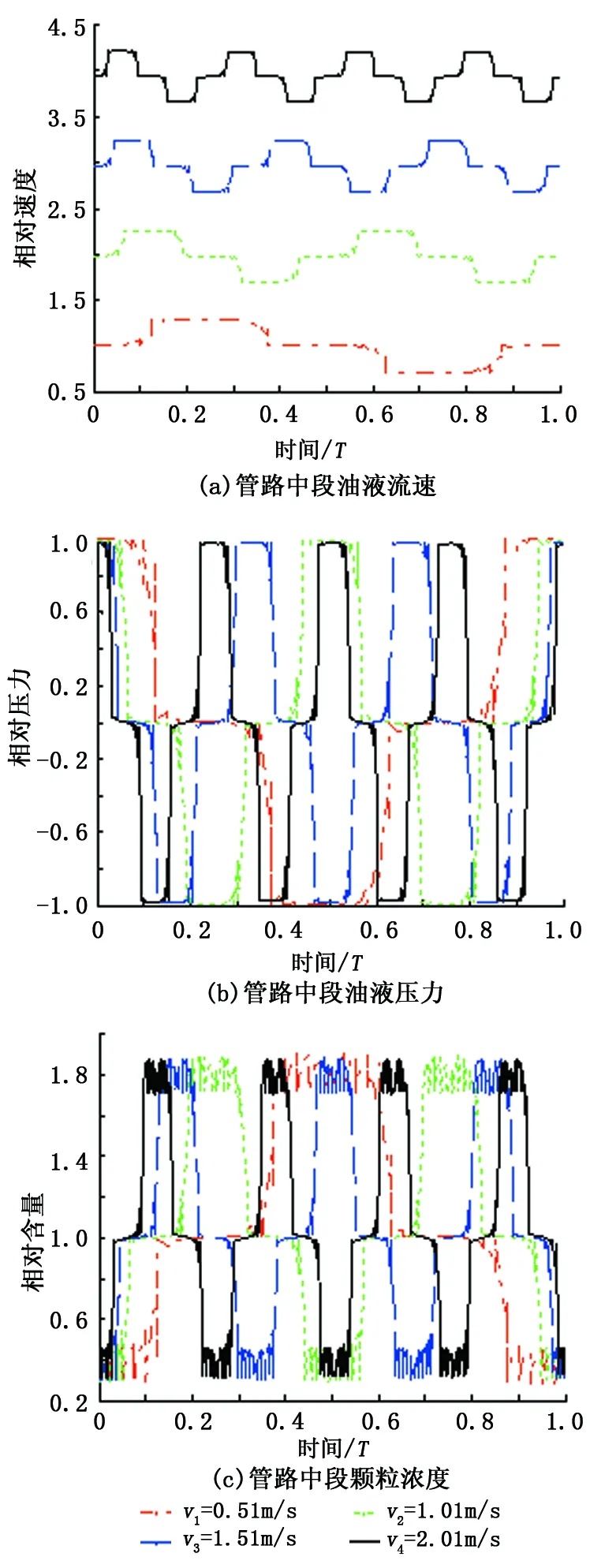
图3 管路中段速度对油液和悬浮颗粒的影响Fig.3 Influence of velocity at middle of pipeline on oil and suspended particles

由图3(c)看出,颗粒浓度的变化趋势与压力趋势相反,在同一个速度条件下它们的周期不变。这是由于在高压时颗粒受到的压降较大,有快速迁移的内在作用力,反之,当压力较低时颗粒受到反向“挤压”的作用力,因而颗粒的浓度就会较大。

(3)管路末端速度对油液、悬浮颗粒的影响。不同初始速度条件下管路末端处油液及颗粒的参数变化情况如图4所示。管路末端是第一次压力波产生的位置,因而从图4(a)与图3(a)、图2(a)比较可知,它们的响应时间依次为0、T/8、T/4。图4(a)中油液流速的变化周期更加明显,前半部分为速度增加段,后半部分为速度下降段。

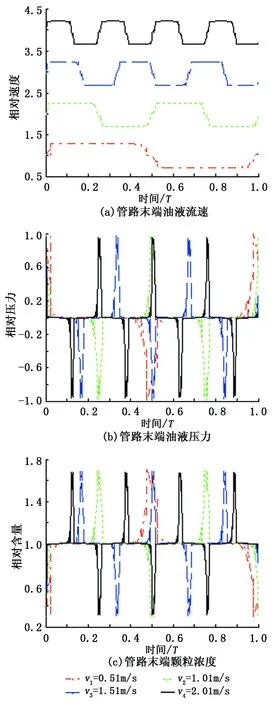
图4 管路末端速度对油液和悬浮颗粒的影响Fig.4 Influence of velocity at end of pipeline on oil and suspended particles

由于管路末端压力的设定原因,在图4(b)中油液压力分别在0、T/2、T时刻,即T/4的偶数倍时产生跃变,很快就恢复到设定压力值。同理油液的流速和压力的脉动周期随着初始速度的增加而减小。

由图4(c)看出,颗粒浓度与油液压力是密切相关的,当任一初始速度下油液压力下降时,颗粒浓度得以释放而升高。

3 结 论

(1)建立油液与其中颗粒物的悬浮流动力学模型,通过特征线法求解,将数值解与实验数据进行比较,所建模型能够较好地反映悬浮流中各相的动态特征,对于分析油液与悬浮颗粒的参数具有可行性。

(2)在设定的含悬浮颗粒油液系统参数情况下,通过不同的初始速度,对管路始端油液压力、流速以及颗粒的流速、浓度分布进行分析。获得不同初始速度条件下油液压力、流速的变化趋势,油液压力、流速在T/4的奇数倍时产生跃变,且随着初始速度的增加循环周期减小。悬浮颗粒浓度分布与油液压力趋势相反,颗粒速度不随油液速度的变化而变化。

(3)在管路中段,油液压力、流速的脉动时刻提前T/8时间,在T/4整数倍时刻都会产生跃变;同理油液压力、速度的脉动周期随着初始速度的增加而减小;悬浮颗粒的浓度分布主要受油液压力的影响,在压力降低时浓度升高,反之亦然。

(4)管路末端是由于压力、流速产生脉动的位置,不同初始速度条件下它们产生跃变的时刻相同,都是T/4的偶数倍时刻。悬浮颗粒的浓度呈现出与油液压力相反的变化趋势,但产生跃变的时刻相同。

[1] 陈彬,武宏阳,刘阁,等.基于红外光谱分析含微水绝缘油氧化安定性研究[J]. 中国石油大学学报(自然科学版),2016,40(1):168-176. CHEN Bin,WU Hongyang, LIU Ge, et al. Research on oxidation stability of insulating oil containing trace water based on infrared spectral analysis[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016,40(1):168-176.

[2] 黄中伟,蔡承政,李根生,等.液氮磨料射流流场特性及颗粒加速效果研究[J]. 中国石油大学学报(自然科学版),2016,40(6):80-86. HUANG Zhongwei, CAI Chengzheng, LI Gensheng, et al. Flow behavior and particle acceleration effect of abrasive liquid nitrogen jet[J].Journal of China University of Petroleum(Edition of Natural Science), 2016,40(6):80-86.

[3] MAN C, TSAI C W. Stochastic partial differential equation-based model for suspended sediment transport in surface water flows[J]. Journal of Engineering Mechanics, 2007,133(4):422-430.

[4] FU X, SUN Q, WANG G, et al. Kinetic modeling of dilute solid-liquid two-phase flows with inelastic collisions[J].Chinese Science Bulletin, 2009,54(23):4358-4364.

[5] 盛晓飞.两相流流动扩散模型的建立及数值模拟[D]. 哈尔滨:哈尔滨理工大学, 2012. SHENG Xiaofei. Study on establishment and numerical simulation of two-phase flow diffusion model[D].Harbin: Harbin University of Science and Technology,2012.

[6] 李洪州,刘大有.高压段含有颗粒的含灰气体激波管流动数值模拟[J].空气动力学学报,1995,13(3): 239-247. LI Hongzhou, LIU Dayou. Numerical simulation of flow in a shock tube with dust in the high pressure section[J]. Acta Aerodynamics Sinica, 1995,13(3):239-247.

[7] MUSTE M. Two-phase versus mixed-flow perspective on suspended sediment transport in turbulent channel flows[J]. Water Resources Research, 2005,41(10):768-778.

[8] HSU T, JENKINS J, LIU P. Simulation of sediment suspension using two-phase approach[C]. Oceans, 2001:1386-1395.

[9] FU X, WANG G,DONG Z. Theoretical analysis and numerical computation of dilute solid/liquid two-phase pipe flow[J]. Science in China (Ser E), 2001,44(3):298-308.

[10] RIJN L C V. Sediment transport(II):suspended load transport[J]. Journal of Hydraulic Engineering, 1984,110(11):1613-1641.

[11] MORTEN L, ZARRUK G A. Particle transport in semi-dilute turbulent pipe flow[J]. Journal of Dispersion Science and Technology, 2015,36(10):1513-1526.

(编辑 刘为清)

Influence of oil velocity on characteristics of suspension flow

CHEN Bin, LIU Ge

(EngineeringResearchCenterforWasteOilRecoveryTechnologyandEquipment,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)

The normal operation of the equipment can be affected significantly by the oil containing particles. In this study, the dynamic characteristics of each phase in the suspension flow of oil containing suspended particulate at different initial velocities were investigated. And a kinetic model of oil containing suspended particles was established based on continuous medium model, which was resolved numerically through the characteristic method to obtain the change trend of each phase parameter at different initial velocities. It is found that under the condition of different initial velocities, the oil pressures and flow rates at the beginning, middle and end of pipeline, are jumped inT/4 odd times, integer times and even times respectively. And their cycles decrease with the increase of initial velocity. Also, the change trend of the concentration distribution of suspended particles is opposite with that of oil pressure.

continuous medium model; characteristic method; oil velocity; suspended particle; concentration distribution

2017-01-15

国家自然科学基金项目(51375516)

陈彬(1972-),男,教授,博士,研究方向为油液污染控制技术。 E-mail:hustchb@163.com。

1673-5005(2017)04-0167-07

10.3969/j.issn.1673-5005.2017.04.022

TE 319

A

陈彬,刘阁.油液速度对悬浮流特性的影响分析[J].中国石油大学学报(自然科学版),2017,41(4):167-173.CHEN Bin, LIU Ge. Influence of oil velocity on characteristics of suspension flow[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(4):167-173.