2D-C/SiC复合材料偏轴拉伸力学行为研究
2017-07-25吴亚波郭洪宝贾普荣
王 波,吴亚波,郭洪宝,贾普荣,李 俊
(西北工业大学 力学与土木建筑学院,西安 710072)
2D-C/SiC复合材料偏轴拉伸力学行为研究
王 波,吴亚波,郭洪宝,贾普荣,李 俊
(西北工业大学 力学与土木建筑学院,西安 710072)
通过对2D-C/SiC复合材料试件进行不同偏轴角度的拉伸实验,研究了偏轴角度对材料拉伸力学特性的影响。通过应变片分别测得了材料加载方向和纤维束方向上的应力-应变行为,对比分析了偏轴角度对上述应力-应变行为的影响;并结合试件断口扫描电镜照片,阐释了纤维束方向上拉伸和剪切损伤间的相互耦合效应。实验结果表明,材料的拉伸模量和强度随偏轴角度的增大出现明显下降;材料纤维束方向上的拉伸损伤和剪切损伤具有显著的相互促进作用。最后,以材料0°拉伸和45°拉伸实验数据为基础,建立了材料的偏轴拉伸应力-应变行为预测模型,模型预测结果与实验结果吻合较好。
2D-C/SiC复合材料;偏轴拉伸;应力-应变行为;损伤耦合;预测模型
连续纤维增强陶瓷基复合材料作为新一代高温热结构材料,在航空航天领域具有广阔的应用前景[1,2],2D-C/SiC复合材料是其中具有代表性的一种超高温结构材料,具有比强度高、比模量高、断裂韧性好以及耐高温、热稳定性好等优点,因此应用前景十分广阔[3]。由于2D-C/SiC复合材料在实际工程应用中一般承受复杂载荷,局部材料的受载方向与纤维束方向(材料主方向)通常存在一定的偏角,使得对材料的偏轴拉伸力学行为研究具有重要的工程意义。
目前,研究者对C/SiC复合材料的基本力学性能和疲劳性能等已做了大量的研究[4,5],而对2D-C/SiC复合材料的偏轴拉伸力学行为的研究还处于初步阶段。李俊等[6]通过实验和理论分析,研究了2D-C/SiC复合材料45°偏轴拉伸和剪切应力-应变行为,发现材料的力学行为随偏轴角度变化显著。甄文强等[7]对2D-C/SiC复合材料进行了30°和45°偏轴拉伸实验研究,并基于修正的经典层合板理论对材料的偏轴拉伸应力-应变行为进行了模拟预测。Nozawa等[8]对2D-SiC/SiC复合材料进行了偏轴拉伸和压缩实验,对比分析了材料在不同偏轴角度下的损伤失效模式和对应的强度分布特征。Weigel等[9]通过对比C/SiC复合材料偏轴拉伸、单一轴向拉伸和剪切应变数据,证明了偏轴拉伸过程中材料存在拉剪损伤耦合效应。Genin等[10]基于陶瓷基复合材料的轴向和45°方向双轴拉伸应力-应变行为,建立了平面应力状态下材料的唯象本构模型,并应用于缺口试件的应力-应变行为预测。此外,Baste[11]和Camus[12]分别对2D-C/SiC和2D-SiC/SiC复合材料进行了偏轴拉伸实验,利用所得实验数据辅助建立了材料的连续损伤本构模型并对其进行了验证。上述工作对平纹编织陶瓷基复合材料的偏轴拉伸力学行为进行了充分的实验和理论研究,但是研究内容主要集中于材料加载方向上的应力-应变行为,并没有对偏轴加载状态下材料主方向上的应力-应变行为展开研究,对材料主方向上的拉剪损伤耦合效应也没有进行深入的分析。
本工作通过对2D-C/SiC复合材料进行0°,15°,30°和45°偏轴拉伸实验,分别获得了材料加载方向和主方向上的拉伸和剪切应力-应变行为,并结合试件断口扫描电镜照片对材料主方向上的拉剪损伤耦合效应进行了分析讨论。最后通过应力下降差值计算,并基于0°和45°偏轴拉伸实验数据,建立了材料的偏轴拉伸应力-应变行为预测模型。
1 实验材料与方法
本工作所用的2D-C/SiC复合材料采用化学气相渗透(CVI)工艺制备而成。首先将T300平纹编织碳纤维布叠层成预制体,然后利用CVI工艺依次沉积厚度约为200nm的热解碳层和SiC基体,然后依据所需试件形状对原材料平板进行剪裁,最后在试件材料表面继续沉积一层SiC防氧化涂层。最终试件材料的平均密度约为2.0g/cm3。偏轴拉伸试件采用长条形,均匀实验段长度为50mm,中间矩形截面宽度和厚度分别为10mm和3mm。试件均匀实验段内的材料纤维束方向分布和应变片粘贴细节如图1所示。其中x-y坐标系位于材料加载和垂直加载方向,σx为施加应力;L-T坐标系位于材料纤维束方向,即材料主方向,θ为拉伸偏轴角度;1号和2号0°/90°应变片分别监测材料x(y)和L(T)方向上的线应变。
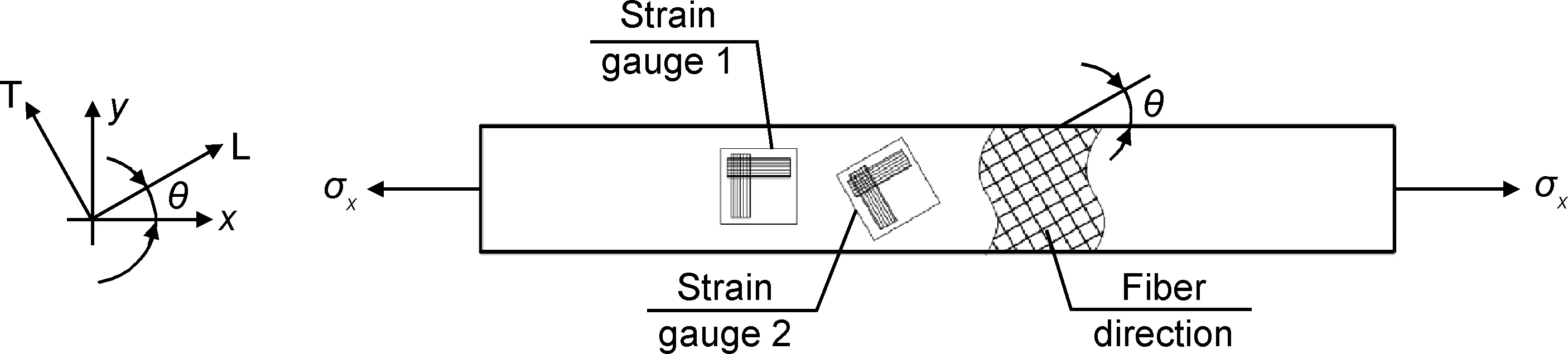
图1 偏轴拉伸试件材料纤维束分布方向和应变片粘贴方式 Fig.1 Fiber bundles’ distribution of off-axis tensile specimen and locations of strain gauges
拉伸实验在INSTRON 5567试验机上进行,加载速率为0.3mm/min,数据采样频率为2Hz。实验过程中通过试件表面粘贴的应变片,配合DH3815N静态应变采集系统,与拉伸载荷同步对材料不同方向的应变数值进行实时采集。
2 结果与分析
2.1x-y方向应力-应变行为
不同偏轴角度下2D-C/SiC复合材料的x-y方向拉伸应力-应变曲线如图2所示,其中x和y方向应变均由1号应变片测得。由图2可见,不同偏轴角度下材料的拉伸响应都表现出显著的非线性特征,且随着偏轴角度的增大而越发显著。对比发现,随着偏轴角度的增大,材料加载方向上的初始拉伸模量和拉伸强度不断降低,而拉伸断裂应变和x-y方向泊松比数值不断增大。
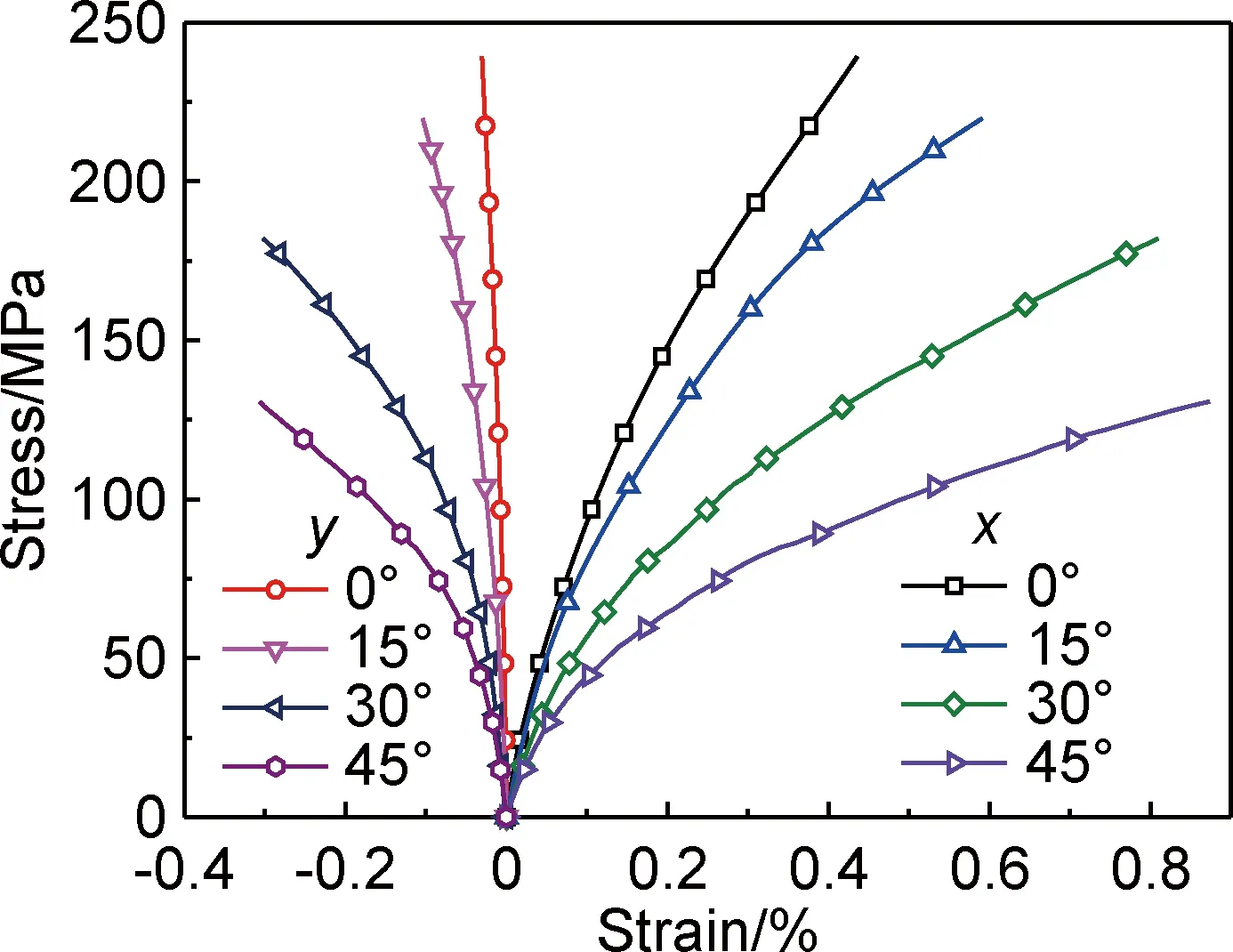
图2 不同偏轴角度下材料x-y方向拉伸应力-应变曲线Fig.2 Tensile stress-strain curves in the x-y direction of the material with different off-axis angles
随着偏轴角度的增大,材料加载方向上SiC基体的模量贡献比例和碳纤维的载荷承担比例都在不断下降,进而导致材料的初始拉伸模量不断减小。同时,拉伸过程中相邻基体裂纹面间桥连纤维的载荷传递机制的效率也在不断下降[10],进一步导致了碳纤维载荷承担比例的下降,并最终促使SiC基体的裂纹密度显著增加[13]。同等施加应力水平下,SiC基体裂纹密度的增加会加速材料的损伤失效进程,使得材料的拉伸应力-应变行为具有更显著的非线性特征,并最终导致材料拉伸强度的下降。基体裂纹密度的增加也会使材料x-y方向泊松比数值增大。此外,随着偏轴角度的不断增大,材料主方向上的拉剪损伤耦合效应也越发凸显,同样也会造成上述材料力学行为的变化。
2.2 L-T方向应力-应变行为
如图3所示,对2D-C/SiC复合材料施加偏轴拉伸载荷,等效于在材料L-T主方向上同时施加等比例变化的双轴拉伸载荷和剪切载荷。依据应力转轴公式,材料L-T主方向上应力分量与偏轴角度θ和施加应力σx之间具有如下关系:
σL=cos2θ·σx
σT=sin2θ·σx
τLT=-cosθ·sinθ·σx
(1)
由式(1)可知,整个加载过程中σL,σT和τLT的数值大小均随σx等比例变化。
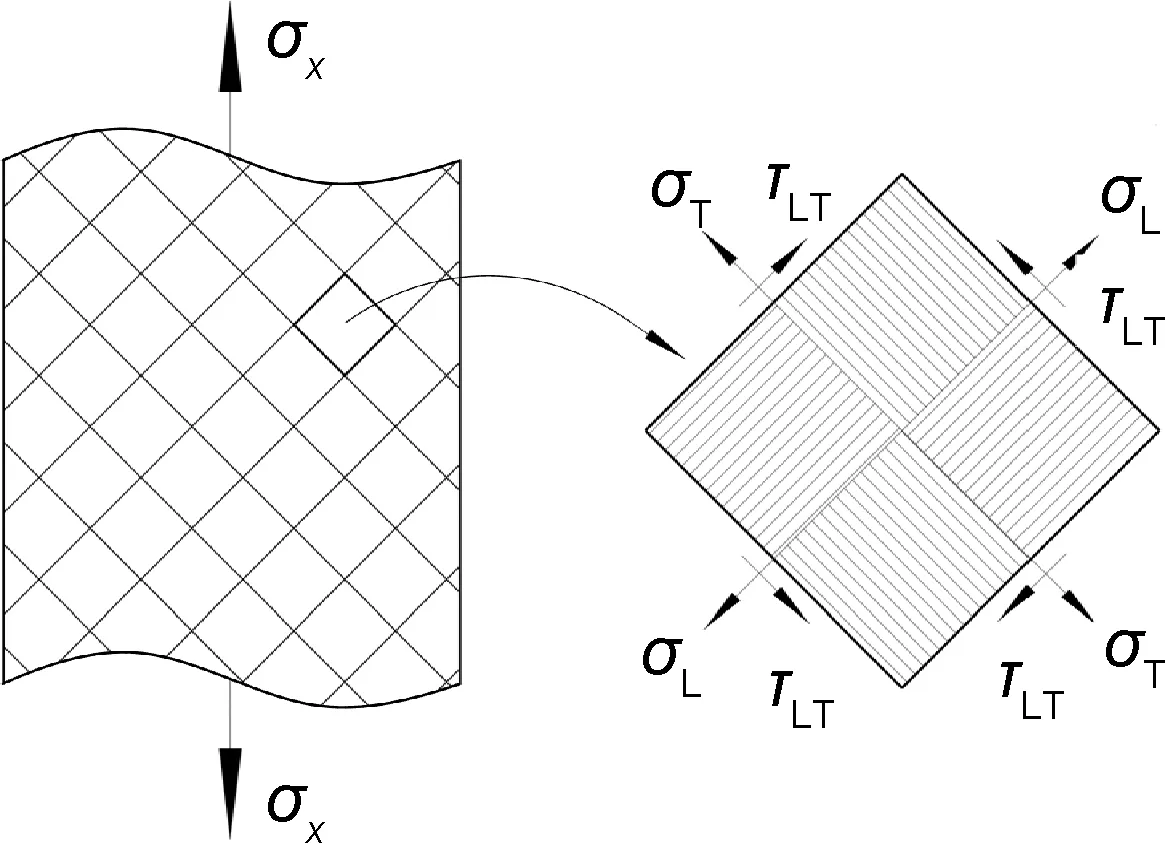
图3 偏轴拉伸状态下材料L-T主方向上的应力状态Fig.3 Stress state in the L-T direction of the material under off-axis tensile loading
依据应变转轴公式,可以得到材料x-y方向和L-T方向上应变分量具有如下关系:
γLT=-2cosθ·sinθ·εx+2cosθ·sinθ·εy+
(cos2θ-sin2θ)·γxy
γxy=2cosθ·sinθ·εL-2cosθ·sinθ·εT+
(cos2θ-sin2θ)·γLT
(2)
整理可得:
(3)
其中εL,εT,εx和εy均由应变花直接测得。综上所述,由测得的实验数据并通过式(1)和式(3)计算,可以得到偏轴拉伸状态下材料L和T方向上的拉伸应力-应变行为和L-T方向上的剪切应力-应变行为。
15°, 30°和45°偏轴拉伸状态下材料L-T主方向上的应力-应变曲线如图4所示。可以看出,材料L,T方向上的拉伸应力-应变行为和L-T方向上的剪切应力-应变行为都与单一轴向拉伸或剪切载荷作用下材料的应力-应变行为相似,均具有显著的非线性特征。但是在同等剪切应力水平作用下,偏轴加载状态下测得的材料L-T方向剪切应变明显大于单一轴向剪切载荷作用下测得的剪切应变[14],说明偏轴拉伸状态下材料L-T方向存在更为严重的剪切损伤。此外,当θ=15°和30°时,同等拉伸应力水平下材料T方向拉伸应变明显大于L方向,说明材料T方向的拉伸损伤程度明显高于L方向。分析可知上述差异均由材料L-T主方向上的拉剪损伤耦合效应引起,并受σL,σT和τLT三者数值比例大小的影响。当θ=45°时,材料L和T方向拉伸应力-应变曲线基本重合,这是由于材料性能相对于加载方向对称导致的。
偏轴拉伸状态下,单独L(T)方向拉伸应力分量σL(σT)会引起材料SiC基体出现T(L)方向上的微裂纹,同时引起L(T)方向上纤维束内部出现界面脱粘、滑移和纤维断裂等细观损伤模式[15];单独L-T方向面内剪切应力分量τLT能够引起SiC基体出现与纤维束呈45°夹角方向上的微裂纹,同时造成L和T方向上纤维束出现径向开裂、界面脱粘和滑移等损伤[9]。可见,当材料L-T方向上同时作用有σL,σT和τLT时,τLT引起的剪切损伤会对材料L和T方向上的拉伸损伤起到促进作用,促进作用随τLT/σL和τLT/σT比值的增大而越发显著;同时σL和σT造成的材料L和T方向上的拉伸损伤也会对L-T方向上的剪切损伤起到促进作用,促进作用随σL/τLT和σT/τLT比值的增大而增大。综上所述,如图4所示,当θ=15°时,σL造成的拉伸损伤对材料L-T方向剪切损伤的促进作用最强,而σT造成的拉伸损伤对材料L-T方向剪切损伤的促进作用最弱;τLT造成的剪切损伤对L方向的拉伸损伤促进作用最弱,而对T方向拉伸损伤的促进作用最强。
2.3 断口形貌分析
为了进一步直观地表征材料在偏轴拉伸载荷作用下的损伤失效模式,并借以阐释材料主方向上的拉剪损伤耦合效应,利用扫描电镜得到的具有不同偏轴角度的试件拉伸断口照片如图5所示。由图5(a)可见,在轴向拉伸载荷作用下,材料加载方向上的纤维束全部发生拉伸断裂,并伴随着较短的纤维拔出;而垂直加载方向上的纤维束发生沿轴向劈裂,束内大部分纤维保持完好;材料内部的基体裂纹取向均与纤维束轴向呈0°或90°。图5(b)中标出的区域为基体裂纹的多发区域,图5(c)和(d)中箭头的方向为基体裂纹方向。由图5(b)~(d)可见,随着偏轴角度的增加,材料内部出现了大量新型基体裂纹,新增裂纹的取向与纤维束轴向大致呈45°夹角,上述基体裂纹主要是由剪切应力分量τLT造成的。此外纤维束断面上的纤维拔出长度也有所增加,说明剪切应力分量也在纤维束内部造成了界面脱粘和滑移等损伤模式。所以在偏轴拉伸加载状态下,由于剪切应力分量τLT的出现,其造成的剪切损伤会加速材料纤维束轴向上的拉伸损伤,反过来拉伸损伤也会不断地促进材料的剪切损伤失效进程,两种损伤间具有相互促进的耦合效应。
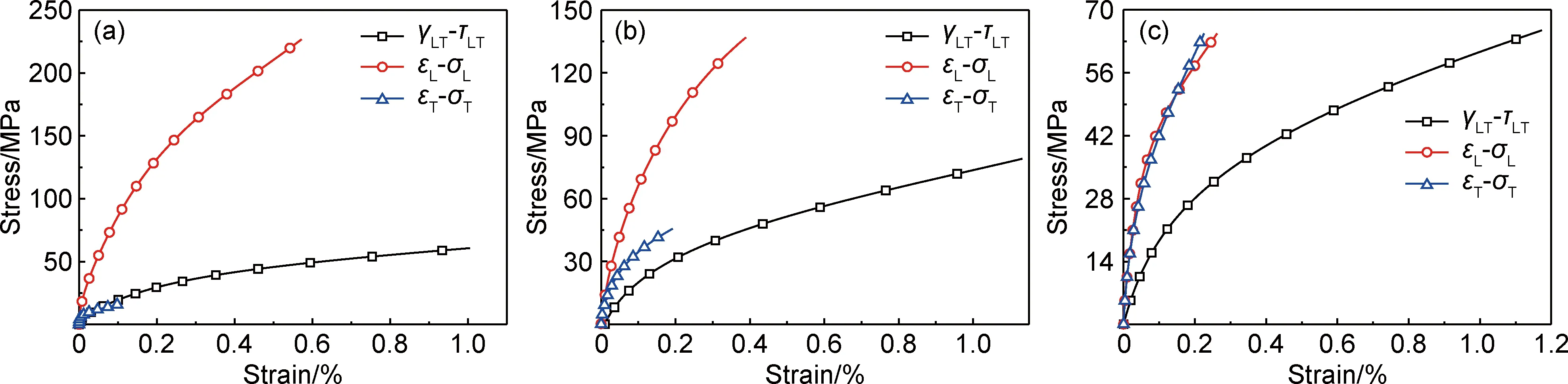
图4 偏轴拉伸状态下材料L-T主方向上的应力-应变曲线 (a)θ=15°;(b)θ=30°;(c)θ=45°Fig.4 Stress-strain curves in the L-T direction of the material under off-axis tensile loading(a)θ=15°;(b)θ=30°;(c)θ=45°

图5 不同偏轴角度下偏轴拉伸试件断口电镜扫描照片 (a)θ=0°;(b)θ=15°;(c)θ=30°;(d)θ=45°Fig.5 SEM images of the fractured surfaces on off-axis tensile specimens with different off-axial angles(a)θ=0°;(b)θ=15°;(c)θ=30°;(d)θ=45°
3 应力-应变行为预测模型
由2D-C/SiC复合材料的0°拉伸应力-应变行为,可以获得拉伸应力与拉伸应变的函数关系为:
(4)
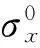
(5)
其中E0为材料0°拉伸初始拉伸模量。同理,依据材料45°偏轴拉伸实验获得的应力-应变行为,可以获得拉伸应力和x方向拉伸应变的函数关系为:
(6)

(7)
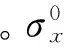
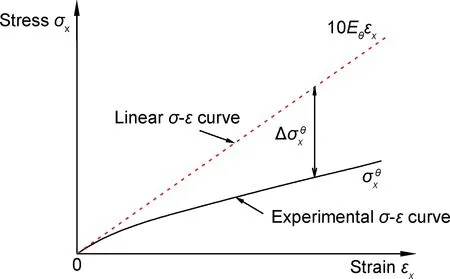
图6 偏轴拉伸状态下轴向应力下降差值示意图off-axis tensile loading
(8)
那么θ角度偏轴拉伸状态下材料x方向应力-应变行为可表示为:
(9)
其中Eθ为材料θ偏轴角度下加载方向初始拉伸模量。依据刚度矩阵转轴公式,得到Eθ的表达式如下:
(10)
其中,GLT为材料L-T方向初始面内剪切模量,v0为0°拉伸时材料x-y方向泊松比。同时可以得到不同偏轴角度θ下材料x-y方向的泊松比vθ为:
(11)
综合式(4)~(11),即可以得到不同偏轴角度下2D-C/SiC复合材料x-y方向的偏轴拉伸应力-应变行为。计算所需材料性能参数一并在表1中给出。

表1 预测模型所需参数数值Table 1 Values of the needed parameters in predictive model
通过上述预测模型,分别对材料15°和30°偏轴拉伸应力-应变行为进行预测,预测结果与实验结果一并在图7中给出。对比发现,在低应力水平下,预测结果与实验结果吻合较好;但是在高应力水平下两者出现一定的偏差。这是因为随着施加应力的增大,材料的损伤不断增加,损伤耦合效应不断凸显,而上述预测模型是通过引入45°偏轴拉伸应力-应变行为来考虑材料的拉剪损伤耦合效应,这会使得模型在高应力水平下的预测值出现一定的偏差。总体而言,模型预测结果与实验结果吻合较好,验证了上述预测模型的准确性。
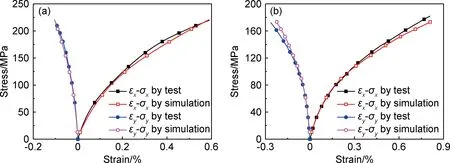
图7 材料偏轴拉伸x-y方向上应力-应变行为预测 (a)θ=15°;(b)θ=30°Fig.7 Prediction in off-axis tensile stress-strain behaviors in the x-y direction of material(a)θ=15°;(b)θ=30°
4 结论
(1) 通过对2D-C/SiC复合材料进行不同角度下的偏轴拉伸实验发现:随着偏轴角度的增大,材料的初始拉伸模量和拉伸强度不断减小,而拉伸断裂应变和泊松比数值不断增大。偏轴加载状态下材料组分间载荷分配比例和载荷传递机制的变化,以及基体裂纹密度的增加是引起上述力学性能变化的主要原因。
(2) 偏轴拉伸状态下,材料L-T主方向上存在着显著的拉剪损伤耦合效应,L和T方向的拉伸损伤与L-T方向的剪切损伤具有相互促进作用,促进作用的强弱受σL,σT和τLT三者数值的比例大小控制。材料主方向上拉剪损伤耦合效应的存在也会造成材料偏轴拉伸力学行为的变化。
(3) 通过引入材料损伤造成的应力下降差值,并基于材料0°和45°偏轴拉伸应力-应变行为,建立了2D-C/SiC复合材料的偏轴拉伸应力-应变行为预测模型。通过对15°和30°偏轴拉伸应力-应变行为进行预测,预测结果与实验结果吻合较好,证明了预测模型的准确性。
[1] 邹武, 张康助, 张立同. 陶瓷基复合材料在火箭发动机上的应用[J]. 固体火箭技术, 2000, 23(2): 60-64.
ZOUW,ZHANGKZ,ZHANGLT.Applicationofceramicmatrixcompositetorocketmotor[J].JournalofSolidRocketTechnology, 2000, 23(2): 60-64.
[2] 张建艺. 陶瓷基复合材料在喷管上的应用[J]. 宇航材料工艺, 2000, 30(4): 14-16.
ZHANGJY.Ceramicmatrixcompositeapplicationinnozzle[J].AerospaceMaterialsandTechnology, 2000, 30(4): 14-16.
[3] 李刚. 二维编织Cf/SiC复合材料力学性能的试验研究[D]. 西安: 西北工业大学, 2007.
LIG.Experimentalstudyonmechanicalpropertyof2-DwovenC/SiCceramicMmatrix composites[D]. Xi’an: Northwestern Polytechnical University, 2007.
[4] 方光武, 高希光, 宋迎东. 针刺C/SiC复合材料拉-压疲劳特性与失效机理[J]. 材料工程, 2016, 44(11): 78-82.
FANG G W, GAO X G, SONG Y D. Tension-compression fatigue behavior and failure mechanism of needled C/SiC composite[J]. Journal of Materials Engineering, 2016, 44(11): 78-82.
[5] 徐立新, 管厚兵, 杨智伟, 等. 真空吸浆法制备C/SiC复合材料及力学性能研究[J]. 材料工程, 2015, 43(12): 10-16.
XU L X, GUAN H B, YANG Z W, et al. Preparation and mechanical property of C/SiC composite by vacuum infusion method[J]. Journal of Materials Engineering, 2015, 43(12): 10-16.
[6] 李俊, 矫桂琼, 王波. 平纹编织C/SiC复合材料层合板面内力学性能的可设计性研究[J]. 机械强度, 2012, 34(2): 229-233.
LI J, JIAO G Q, WANG B. Designable in-plane mechanical property of plain-woven C/SiC composite laminate[J]. Journal of Mechanical Strength, 2012, 34(2): 229-233.
[7] 甄文强, 王波, 李潘, 等. 平纹编织C/SiC复合材料层合板偏轴拉伸性能研究[J]. 机械强度, 2014, 36(6): 856-861.
ZHEN W Q, WANG B, LI P, et al. Study on off-axis tensile properties of plain-woven C/SiC composites[J]. Journal of Mechanical Strength, 2014, 36(6): 856-861.
[8] NOZAWA T, OZAWA K, CHOI Y, et al. Determination and prediction of axial/off-axial mechanical properties of SiC/SiC composites[J]. Fusion Engineering and Design, 2012, 87(5-6): 803-807.
[9] WEIGEL N, KRÖPLIN B, DINKLER D. Micromechanical modeling of damage and failure mechanisms in C/C-SiC[J]. Computational Materials Science, 1999, 16(1-4): 120-132.
[10] GENIN G M, HUTCHINSON J W. Composite laminates in plane stress: constitutive modeling and stress redistribution due to matrix cracking[J]. J Am Ceram Soc, 1997, 80(5): 1245-1255.
[11] BASTE S. Inelastic behaviour of ceramic-matrix composites[J]. Composites Science and Technology, 2001, 61(15): 2285-2297.
[12] CAMUS G. Modelling of the mechanical behavior and damage processes of fibrous ceramic matrix composites: application to a 2-D SiC/SiC[J]. International Journal of Solids and Structures, 2000, 37(6):919-942.
[13] CADY C, HEREDIA F E, EVANS A G. In-plane mechanical properties of several ceramic-matrix composites[J]. J Am Ceram Soc, 1995, 78(8): 2065-2078.
[14] 管国阳, 矫桂琼, 张增光. 平纹编织C/SiC复合材料的剪切性能[J]. 机械科学与技术, 2005, 24(5): 515-517.
GUAN G Y, JIAO G Q, ZHANG Z G. In-plane shear fracture characteristics of plain-woven C/SiC composite[J]. Mechanical Science and Technology, 2005, 24(5): 515-517.
[15] 杨成鹏, 矫桂琼, 王波. 2D-C/SiC复合材料的单轴拉伸力学行为及其强度[J]. 力学学报, 2011, 43(2): 330-337.
YANG C P,JIAO G Q,WANG B. Uniaxial tensile stress-strain behavior and strength of plain woven C/SiC composite[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2): 330-337.
[16] 李俊. 二维C/SiC复合材料非线性本构关系研究[D]. 西安: 西北工业大学, 2014.
LI J. Research on the nonlinear constitutive relationship of 2D C/SiC composites[D]. Xi’an: Northwestern Polytechnical University, 2014.
(本文责编:齐书涵)
Investigation on Off-axis Tensile MechanicalBehaviors of 2D-C/SiC Composites
WANG Bo,WU Ya-bo,GUO Hong-bao,JIA Pu-rong,LI Jun
(School of Mechanics,Civil Engineering and Architecture, Northwestern Polytechnical University,Xi’an 710072,China)
The off-axis tensile mechanical behaviors of 2D-C/SiC composite laminates were obtained by tests under different off-axis angles, and the influence of off-axis angle on the tensile mechanical behaviors was studied. By sticking strain gauges on the surfaces of specimens, the stress-strain behaviors in the loading direction and in the fiber bundle directions of material were obtained and analyzed. Combined with the SEM (scanning electron microscope) results of fractured surfaces on specimens, the coupling effects between tensile and shear damage in the fiber bundle directions were also analyzed. Test results show that the tensile modulus and strength of material decrease significantly with increasing off-axis angle; and there exists obvious mutual effect between tensile and shear damage in fiber bundle orientation. Furthermore, based on the stress-strain data obtained from 0° and 45° tensile tests, a predictive model was built to predict the off-axis tensile stress-strain behaviors of material. The prediction has good agreement with test data.
2D-C/SiC composites;off-axis tension;stress-strain behavior;damage coupling;predictive model
10.11868/j.issn.1001-4381.2015.000582
O34;TB332
A
1001-4381(2017)07-0091-06
西北工业大学超高温结构复合材料国防重点实验室创新基金(6142911050116)
2015-05-11;
2017-04-02
王波(1976-),男,副教授,博士,主要从事复合材料及其结构的力学行为研究,联系地址:陕西省西安市友谊西路127号西北工业大学118信箱(710072),E-mail:b.wang@nwpu.edu.cn
