编织衬垫关节轴承热力耦合分析
2017-07-25赵银龙张瑞邱明段闯创
赵银龙,张瑞,邱明 ,段闯创
(1.宁波曙光机电制造有限公司,浙江 慈溪 315336;2.河南科技大学 机电工程学院,河南 洛阳 471003)
自润滑关节轴承具有体积小、摩擦因数低、质量轻、摩擦力矩小、承载高、易拆装和免保养等特点,广泛应用于各种机械加工设备[1-2]。摩擦温度的急剧上升是关节轴承失效形式中的重要形式。国内外针对摩擦热进行了很多研究。文献[3]提出了摩擦副表面上由于摩擦热不均匀引起摩擦接触区域发生不均匀的变形,从而引起温度波动的理论。文献[4]用有限元方法分析了火车车轮制动过程中摩擦表面上温度的分布和波动规律。文献[5]运用泛函分析方法分析了2个圆柱面摩擦副之间摩擦温升的分布情况,以及摩擦副接触面的宽度、摩擦速度、热分配系数等参数对摩擦温升分布的影响。文献[6]首次提出了“闪温”这个概念,并推导出了摩擦面上最大温升公式。文献[7]研究了摩擦表面之间摩擦温度的数值计算方法,明确了接触表面之间的热边界。文献[8]用解析方法和数值计算方法分析了在瞬时动态条件下,带状接触面上摩擦温度和接触热阻在摩擦副表面和内部的分布情况,以及随着Biot数和Peclet数的变化摩擦温度和接触热阻的变化。文献[9]运用正交层合板理论分析了不同角度下关节轴承衬垫和内圈的接触应力及变形量。文献[10]建立关节轴承的模型,改变球径尺寸得到最佳接触应力所对应的内圈和衬垫之间的间隙值。文献[11]运用有限元软件模拟上下两表面在摩擦过程中的接触压力、温度分布,并讨论了热膨胀系数、比热、弹性模量、热传导率等材料参数对接触比率的影响。上述研究主要集中于摩擦副的热力学仿真,分析应力、应变、摩擦温度及配合间隙等的变化规律及影响因素。现有研究中还有很多关于摩擦温升和热力耦合的有限元研究[12-14],而关于关节轴承的仿真大多局限于应力应变分析及结构优化。因此,现利用ABAQUS软件建立编织衬垫关节轴承的动态热力耦合模型,通过试验对仿真模型进行验证,在此基础上分析摩擦温度的分布规律及其对关节轴承结构力学性能的影响。
1 编织衬垫关节轴承热力耦合模型
1.1 模型假设
由于编织衬垫关节轴承实际工作时传热情况复杂,相关材料性能会随温度发生变化,要建立关节轴承的详细模型非常困难。因此,对模型进行简化,并作以下假设:室温设定为20 ℃;由于热量主要集中在摩擦副之间,热辐射很小,所以忽略热辐射的影响;编织衬垫关节轴承热传导系数、与空气对流换热系数、摩擦副之间摩擦因数、材料密度以及热膨胀系数设为常量;考虑到编织衬垫关节轴承外圈的变形对整个模型计算结果的影响不大,把外圈设置成刚体进行求解分析。
1.2 模型建立
1.2.1 材料参数
编织衬垫关节轴承GE20ET-2RS套圈采用GCr15轴承钢,为各向同性材料;衬垫为聚四氟乙烯和芳纶纤维编织而成的自润滑衬垫,为各向异性材料。
运用ABAQUS有限元软件建立编织衬垫关节轴承热力耦合模型,各零件材料热学参数和力学参数见表1。由于衬垫是各向异性材料,所以其弹性参数(弹性模量E、剪切模量G、泊松比ν)在各个方向是不同的。

表1 轴承零件热学模型和力学模型参数
1.2.2 边界条件
在外圈上建立一个参考点RP1,把外圈外表面耦合到RP1上,向RP1添加35 kN沿y方向的集中载荷,同时在内圈中心建立参考点RP2,把内圈内表面耦合到RP2上,衬垫和外圈通过绑定约束来模拟实际的粘贴过程,衬垫内表面和内圈外表面定义面对面的接触属性,摩擦因数为0.05。开始加载时固定参考点RP2,等效于通过内孔固定关节轴承内圈。加载完毕进入到第2分析步时,内圈开始在受力的情况下进行旋转摆动,通过添加一个正弦的幅值曲线来实现在同一分析步骤下的往复旋转摆动。添加在关节轴承内圈孔中心的参考点RP2上的旋转边界条件为
θ=0.174 5sin(4πt),
(1)
式中:θ为内圈瞬时旋转摆动角度,rad。
1.2.3 网格划分
由于外圈采用解析刚体,故只对内圈和衬垫进行网格划分。单元类型选择C3D8RT三维八节点实体减缩积分单元,采用扫略式划分网格(图1),内圈得到15 750个单元,衬垫得到8 322个单元。

图1 网格划分
2 仿真分析
在摆动角度为±10°,径向载荷为35 kN,摆动频率为2 Hz的试验条件下对衬垫和内圈进行仿真分析。
2.1 云图分析
通过ABAQUS仿真分析得到衬垫和内圈的摩擦温度、等效应力及位移云图分布分别如图2、图3所示。从图2a、图3a可以看出,衬垫和内圈温度最大值均位于接触中心位置,呈环形向四周递减,其中衬垫温度最大值为47.12 ℃,内圈温度最大的为57.65 ℃。从图2b可以看出,衬垫等效应力沿圆周方向呈线条状分布,衬垫最大等效应力为526.5 MPa,分布在衬垫的2个端面边缘位置;内圈的最大等效应力为207.3 MPa,位于内圈的内部,而非接触表面(图3b)。由于材料的非均匀性,使得衬垫位移的分布也呈现非均匀性,最大位移量为39 μm(图2c)。云图中显示的只是衬垫各个节点和单元相对于原始位置的位移变化量,计算过程中引起衬垫位移变化的除了受力之外,还有温度引起的热膨胀对衬垫位移分布的影响,内外圈之间的间隙也是衬垫位移的一部分。所以云图中的最大位移量并不是衬垫的变形量,而是受力、热以及间隙引起的综合位移。从图3c可看出,内圈的变形量从表面到内部逐渐减小,接触区域变形较大,但从接触区域向两边变形分布不对称,这是由于在旋转过程中内圈受到摩擦力的作用引起旋转方向上等效应力分布不对称。分别沿3种不同路径(图4)提取相应节点上的值绘制曲线作进一步分析。

图2 衬垫云图

图3 内圈云图

图4 切割路径
2.2 温度分析
内圈、衬垫温升分布曲线如图5所示。从整体来看,内圈与衬垫的最大温升均位于接触中心。图5a中,衬垫沿轴向最大温升为27.12 ℃,两端面最小温升为24.75 ℃,最大温差为3.5 ℃,整体温升分布比较平滑;内圈最大温升为37.65 ℃,最小温升为27.5 ℃,最大温差为10 ℃,与衬垫沿轴线方向的温差相比较大。整体温升分布沿轴线方向呈现中间高两边低的趋势,且峰值部分宽度较大,说明内圈接触部分温度分布较平稳,靠近曲线两边位置为非接触区域,温度急剧降低。图5b中,衬垫沿圆周方向最大温升与沿轴线方向最大温升在同一位置,大小相等,最小温升为12 ℃,最大温差为15.12 ℃,整体分布也呈现中间高两边低的趋势;内圈最大温升(37.65 ℃)也位于接触中心位置,最小温升为10 ℃,最大温差为27.65 ℃,大于衬垫沿圆周方向的温差(15.12 ℃)。图5c中,从表面到1 mm深度时,内圈温升随深度的变化呈现线性变化;从1 mm到内孔表面,内圈的温升随深度的变化呈现非线性变化。在深度方向上,内圈的整体温差在6.65 ℃左右。对比图5a和图5b可以看出,衬垫的温升和最大温差均小于内圈。
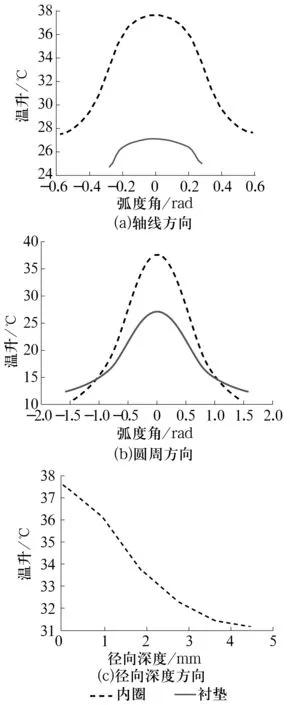
图5 内圈和衬垫沿不同路径的温升曲线
2.3 应力分析
为研究摩擦温度与关节轴承工作时应力、应变的内在联系,对有、无摩擦热时关节轴承各零件的等效应力和变形进行计算,并分析摩擦热对关节轴承力学特性的影响规律,衬垫和内圈接触面上的等效应力分布分别如图6、图7所示。由图6可知,有摩擦热时,衬垫各个方向上的等效应力均大于无摩擦热时,且应力变化的程度沿接触面中心向四周递减。对比温度分布曲线可知,温度越高,衬垫等效应力变化越大。由图7a、图7b可知,关节轴承摩擦表面最大等效应力位于摩擦副的接触中心,有摩擦热时,内圈接触区域等效应力在各个方向上小于无摩擦热时;在非接触区,由于摩擦副上产生的热量经过热传导传递到非接触区域,因而也产生微小的应力。所以对于内圈,适量的摩擦热有助于缓解应力。由图7c可知,最大等效应力位于内圈内部距离摩擦表面3 mm的深度位置,且最大值在无摩擦热时为250 MPa,有摩擦热时减小到160 MPa。
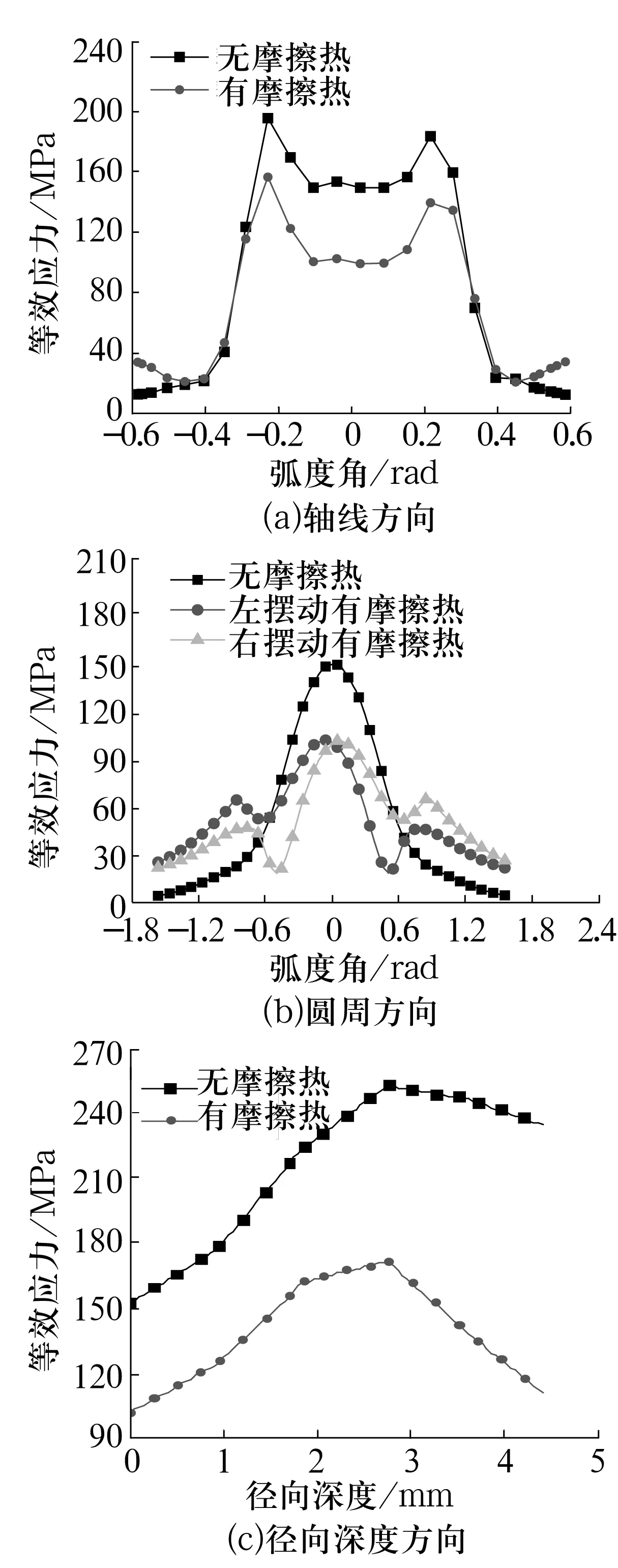
图7 内圈接触面应力分布
2.4 变形位移分析
衬垫和内圈接触面位移分布曲线图分别如图8、图9所示。从图8a可以看出,衬垫沿轴线方向变形量在有摩擦热时明显小于无摩擦热时。为了便于分析,对图8b中的曲线进行处理,选取数据点中相邻的5个点作为平均值进行拟合,通过对比拟合曲线来分析摩擦热对关节轴承衬垫变形的影响。从图中可以看出,在无摩擦热时,衬垫接触中心位置位移量小于非接触区,这是由于当外圈和衬垫受外力与内圈接触过程中,接触部分的衬垫位移不变,但由于接触部分的变形,非接触部分受到牵引,在沿受力方向上发生位移使受力平衡。因此,非接触区域在整个加载过程中具有最大的位移量。衬垫在有摩擦热时整体位移量变小,说明衬垫在受力压向关节轴承内圈的时候受到了内圈热膨胀的影响,使得衬垫回弹,从而使整体移动位移变小。此外,有摩擦热时衬垫波动所对应的弧度范围大于无摩擦热时,说明衬垫在有摩擦热时接触面积变大。通过图9可知,在有摩擦热时内圈变形量均小于无摩擦热时。在摩擦温度57.65 ℃下,内圈接触面沿轴线方向上的变形量与无摩擦热时相比减少了2~3 μm。沿深度方向,由摩擦热引起的内圈变形量绝对值逐渐减少(图9c)。
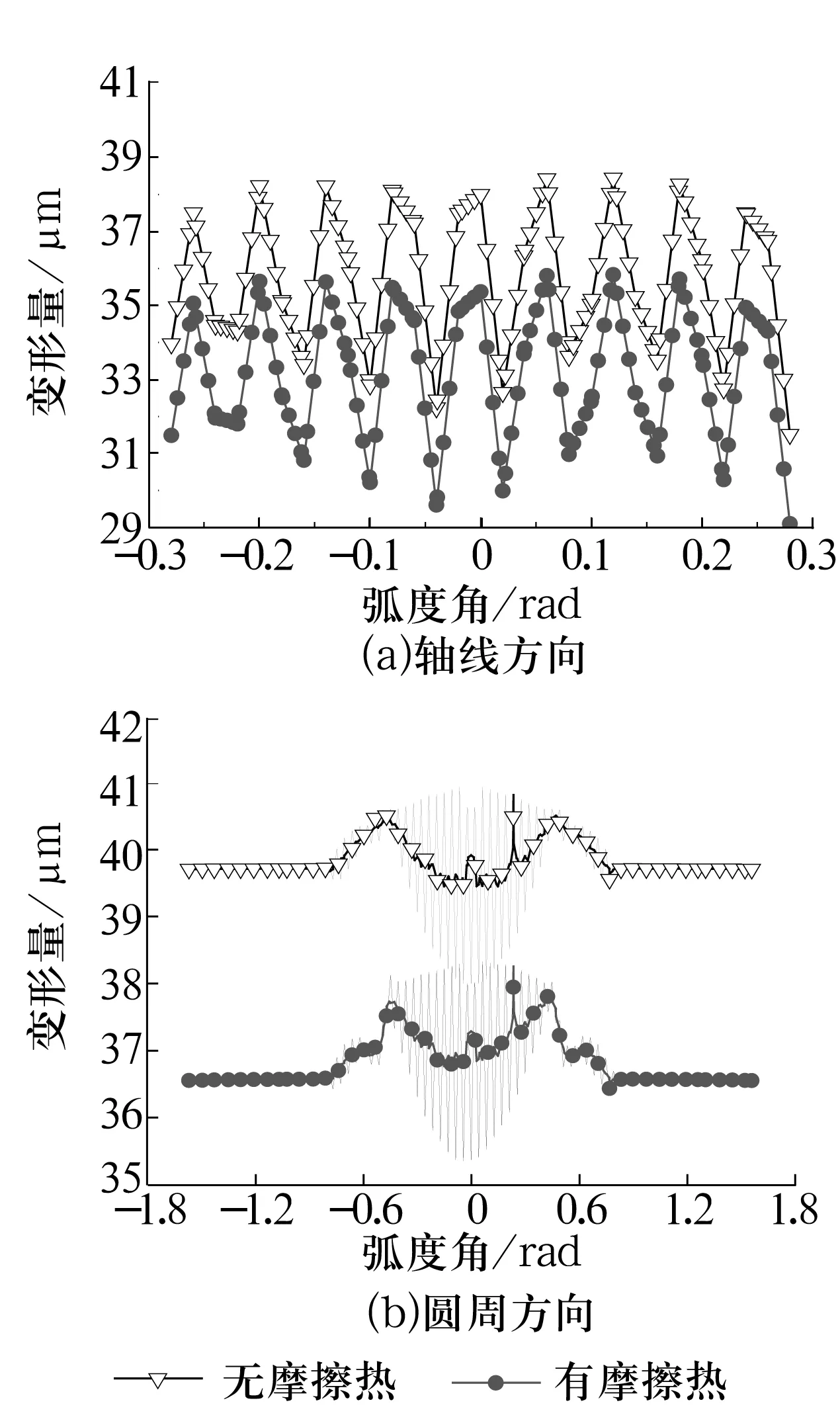
图8 衬垫位移分布
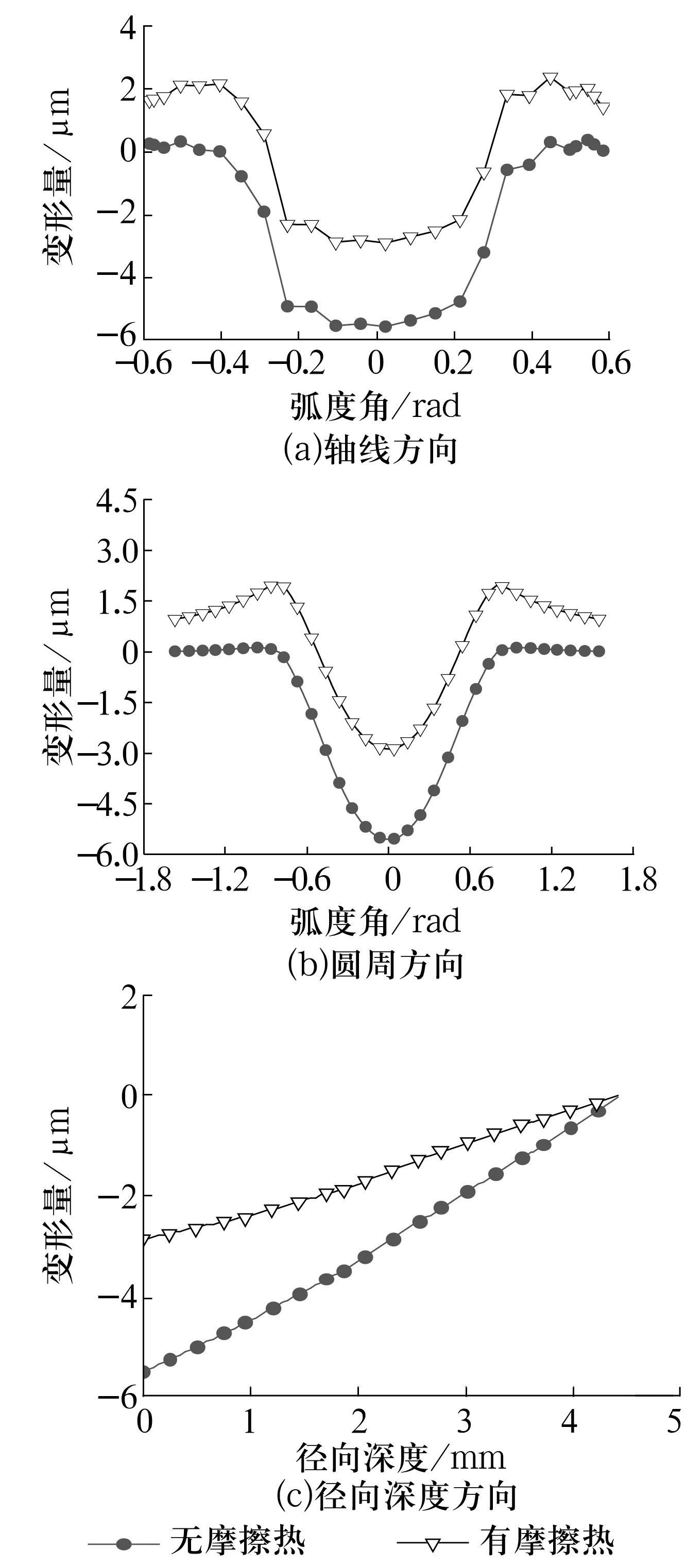
图9 内圈位移分布
3 试验验证
利用自制的关节轴承试验机展开关节轴承摩擦特性试验,对编织衬垫关节轴承温度场进行实时测量。试验机结构及测试系统如图10所示。
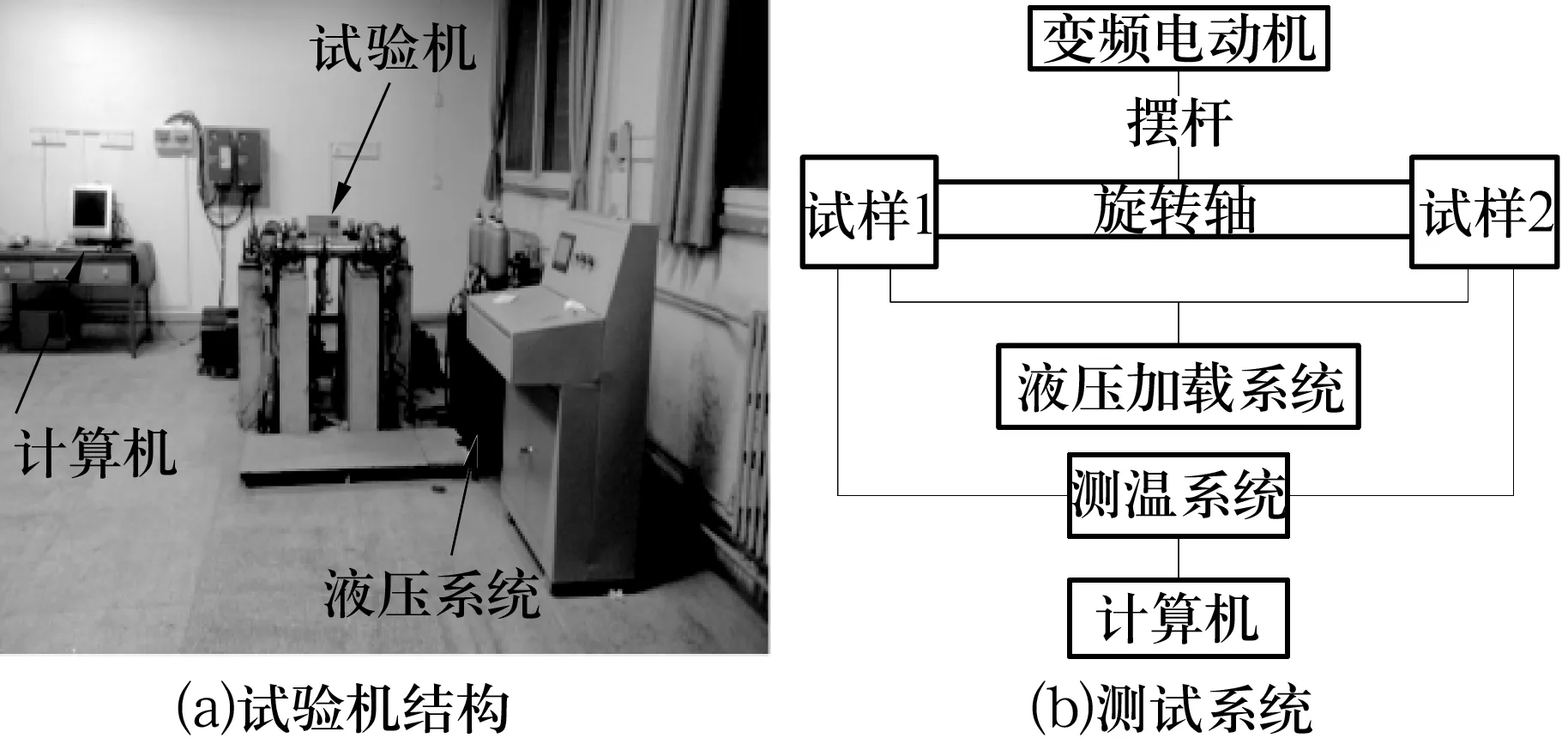
图10 关节轴承温升测试试验机
试验条件:摆动角度±10°,径向载荷35 kN,摆动频率2 Hz,摆动时间300 min。试验前在轴承端面均匀打孔(直径为1 mm,深度为8 mm),通过传感器插入孔内接触式测量轴承温度,试验重复3组,每组2套轴承,结果取均值。内圈结构如图11所示。
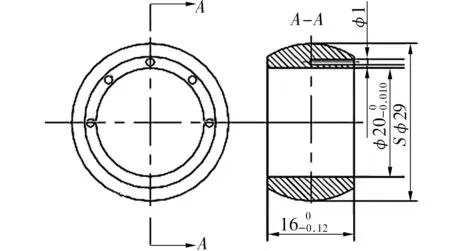
图11 试验轴承内圈结构
提取仿真模型中对应的温度值,绘制内圈圆周方向温度场分布曲线,如图12所示。从图中可以看出,试验值和仿真值的分布趋势一致,在接触中心位置附近试验值稍低于仿真值。这主要是由于接触式测量过程中发生热量损失;由于测孔位置及接触距离误差也会导致测量精度降低;受环境温度等不可预测因素影响也会导致测量误差。但整体上看,仿真值与试验值较为接近,说明了仿真结果的正确性。
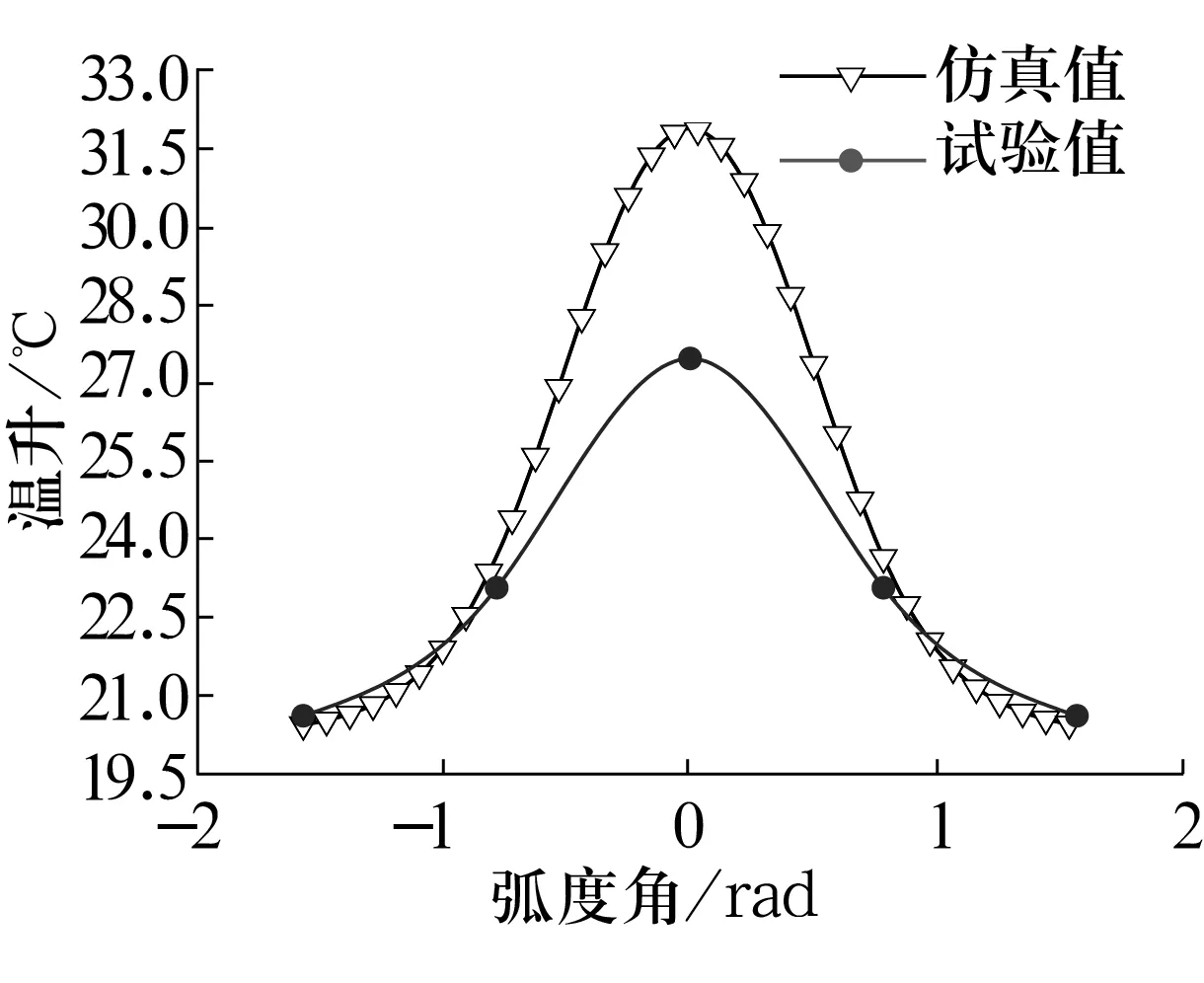
图12 内圈温升场分布曲线
4 结束语
以编织衬垫关节轴承为研究对象,结合ABAQUS仿真软件建立了动态热力耦合模型,分析了关节轴承内圈、衬垫的温度的分布规律,在此基础上研究了摩擦热对关节轴承应力、应变的影响,并通过试验验证了仿真计算结果的正确性。
相较于无摩擦热情况,有摩擦热时内圈和衬垫的变形量变小,在接触区域衬垫变形呈现波动分布,与内圈接触面积变大。适当的摩擦温度可以缓解编织衬垫关节轴承的应力变化,改善关节轴承的力学性能,延长使用寿命。
