深刻而不深奥 简约而不简单——一道高考题的深度思考

陕西省汉中中学(723000) 韩富万

陕西省略阳县天津高级中学(724300) 陈波

深刻而不深奥 简约而不简单
——一道高考题的深度思考

陕西省汉中中学(723000) 韩富万

陕西省略阳县天津高级中学(724300) 陈波

2016年高考数学全国卷I文科第20题是一道关于抛物线的问题.该试题设计结构简洁,整体运算量控制合理,但其背景深刻,意味深长,可谓是深刻而不深奥,简约而不简单.基于此,笔者认为有必要对这道高考试题进行深度的思考探究,一方面揭示此题的背景和本质,另一方面对这道试题进行更一般化的变式拓展.

1 试题及解答

题目(2016年高考数学全国卷I文科第20题)在直角坐标系xOy中,直线l:y=t(t0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.

(2)除H以外,直线MH与C是否有其它公共点?说明理由.

解答(1)由已知得M(0,t),又M关于点P的对称点为N,所以,ON的方程为,代入y2=2px整理得px2−2t2x=0.解得因此所以N为OH的中点,即=2.

2 背景探究— 从数学史的角度看试题背景

该试题本质上就是阿波罗尼奥斯所著《圆锥曲线论》中如下命题:

命题33 如果在一齐曲线上取某个点,从它对直径作出一纵线,它在直径上从顶点截出一线段,又在同一直线(直径)上从端点(在另一侧)量取一线段与上述线段相等,那么连接得到的点和所取点的直线将与这截线相切.

命题35 如果一直线与一齐曲线相切,它与直径在截线之外相交,从切点作对直径的纵线,它将在直径上截出一个从顶点开始的线段,与直径上从截线顶点到切线(与直径的交点)之间的线段相等,而且没有任何直线会落在这切线与这截线之间的孔隙之中.

《圆锥曲线论》的命题中的齐曲线即现代解析几何中的抛物线.圆锥曲线的直径指的是:考虑一个平面上的任一曲线,如果从它画出一直线,它平分着所有平行于某一直线且与这曲线交出的线段,则称这直线为(这曲线的一条)直径.就抛物线而言,其直径也即为平行弦中点轨迹.

以抛物线y2=2px(p>0)为例.设该抛物线任一组斜率为k的平行弦的方程为y=kx+m.设其中任一条弦与抛物线y2=2px交于A(x1,y1),B(x2,y2),两点.由

得

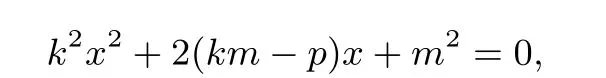
当抛物线的一组平行弦的斜率不存在,显然这一组平行弦中点轨迹就是抛物线的轴.

由此可知,抛物线的轴以及平行于轴的直线都是抛物线的直径.同时需要说明的是,对于其它曲线,其直径可能不是直线.纵线的概念与直径有关,对于每条直径,它所平分的线段的方向都是确定的,这些被直径所平分的线段的方向便是这直径的纵线方向.因此,从现代解析几何的角度看:

命题 33即为:如图 1,直线ABC是抛物线的直径,DP是对直径所作的纵线.取线段BQ=BP,连接QD,则直线QD与抛物线相切于点D.

图1

命题35即为:如图1,直线ABC是抛物线的直径,直线QD与抛物线相切于点D,交直径上一点Q,DP是对直径所作的纵线,则BQ=BP.

显然,命题33与命题35互为逆命题.

通过对这两个命题与这道高考试题之间的必然联系的探究,发现:

③结合题中条件“M关于点P的对称点为N”及以上命题可知(2)问中直线MH是抛物线C的切线,并且切点为H,因此除H以外,直线MH与C没有其它公共点.

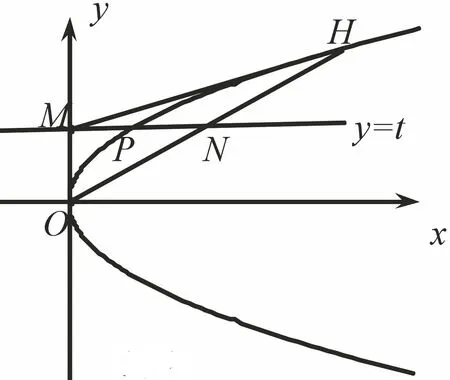
图2

3 变式拓展

由上述分析,笔者对这道高考试题进行了更一般的拓展:

如图3,在直角坐标系xOy中,抛物线C:y2=2px(p>0)的切线为MA,切点为A.直线l:y=t交MA于点M,交抛物线C于点P,M关于点P的对称点为N,连结AN并延长交C于点H.

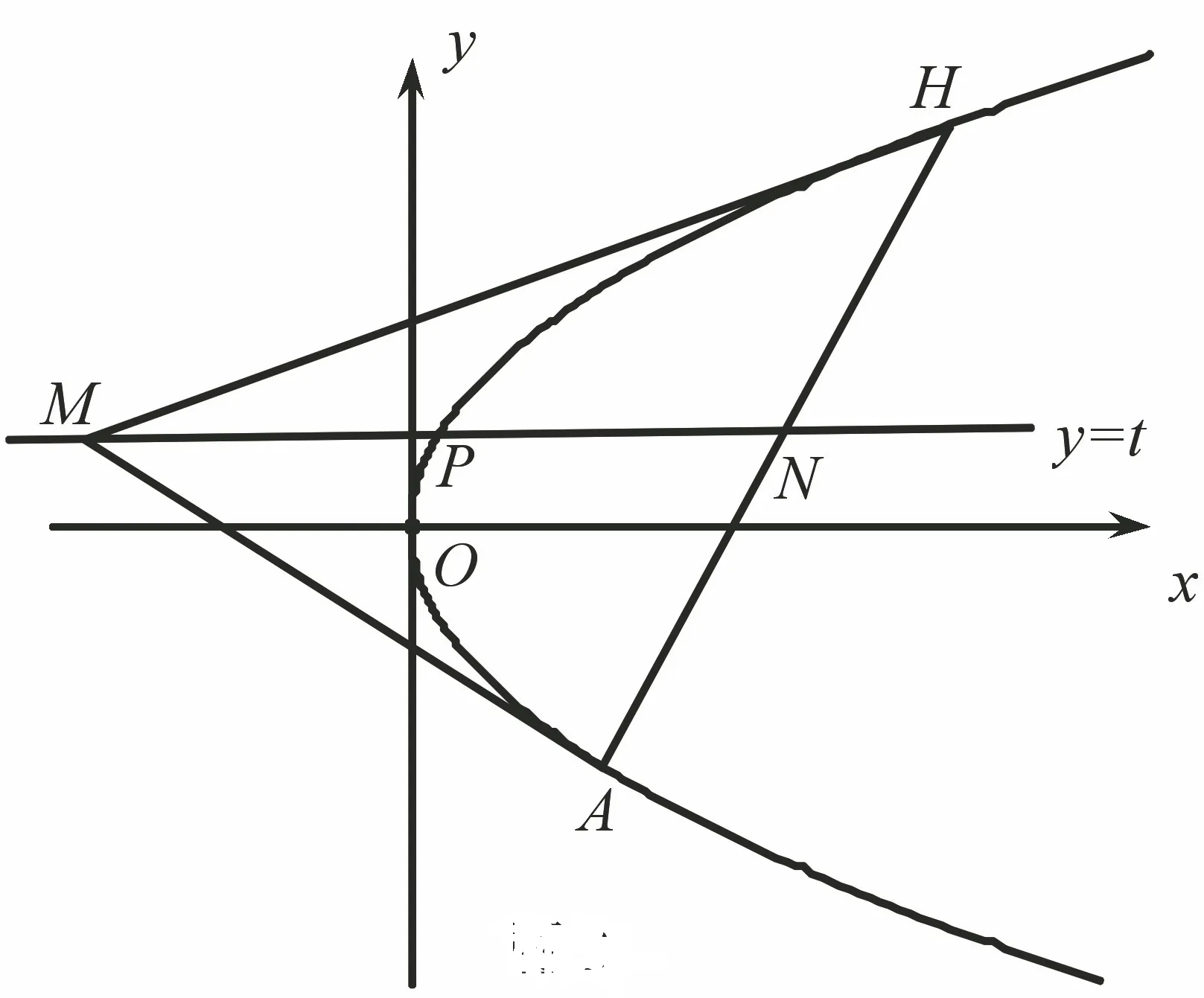
图3

(2)除H以外,直线MH与C是否有其它公共点?说明理由.

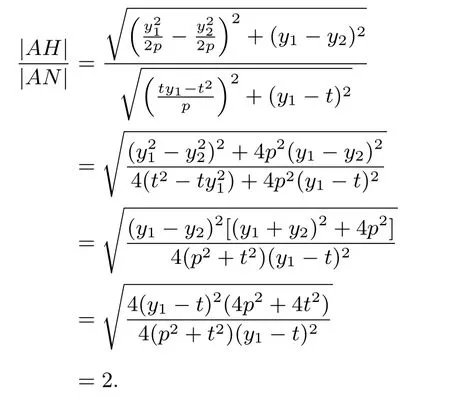
(1)设直线MH上任意一点坐标为Q(x,y).由y1+y2=2t得y2=2t−y1,所以

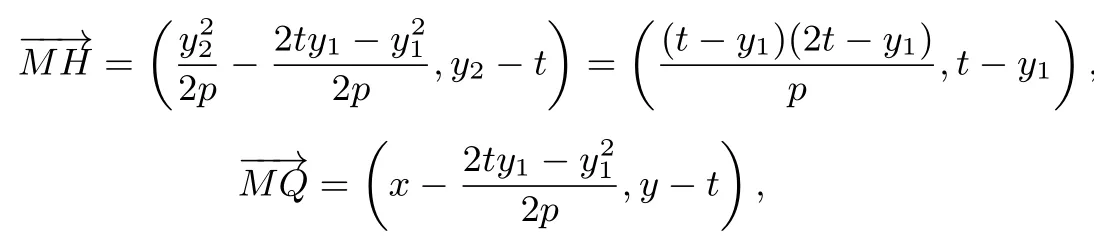
从而得直线MH的方程为:2px−2(2t−y1)y+(2t−y1)2=0.代入抛物线方程y2=2px,得y2−2(2t−y1)y+(2t−y1)2=0,由判别式∆=4(2t−y1)2−4(2t−y1)2=0,即直线MH与C只有一个公共点,所以除H以外,直线MH与C没有其它公共点.

最后,还想说明一点,当图3中的点A与点O重合,则切线MA变为图2中的切线MO,此时呈现在我们面前的就是2016年高考数学全国卷I文科第20题.