深厚覆盖层上土石坝动力分析黏弹性边界处理方法

杨正权，刘小生，汪小刚，赵剑明，温彦锋

（1.流域水循环模拟与调控国家重点实验室，北京 100038；2.中国水利水电科学研究院 岩土工程研究所，北京 100048；3.水利部水工程抗震与应急支持工程技术研究中心，北京 100048）

深厚覆盖层上土石坝动力分析黏弹性边界处理方法

杨正权1，2，3，刘小生1，2，3，汪小刚1，2，3，赵剑明1，2，3，温彦锋1，2，3

（1.流域水循环模拟与调控国家重点实验室，北京 100038；2.中国水利水电科学研究院 岩土工程研究所，北京 100048；3.水利部水工程抗震与应急支持工程技术研究中心，北京 100048）

当覆盖层地基深度相对其上土石坝坝高较大时，大坝动力分析计算中常将覆盖层地基截断，只取临近坝体部分覆盖层地基连同坝体一起作为计算分析对象。用黏弹性边界条件代替固定边界条件，可以消除或有效降低由于截断边界造成外行波无法透过边界而引起的计算误差。本文采用施加等效地震惯性力的方法实现黏弹性边界条件下的地震动输入、采用等效线性化方法反映覆盖层地基边界上黏弹性边界条件的非线性特性，建立了基于黏弹性边界条件的深厚覆盖层上土石坝动力反应分析方法。研究表明：施加等效地震惯性力的方法可以简单而有效地解决黏弹性边界条件下的地震动输入问题；固定边界条件大幅提高了坝体在地震作用下的动力反应水平，使得计算的结果偏于安全。

深厚覆盖层；土石坝；动力分析；边界处理方法；黏弹性边界

1 研究背景

作为大坝地基的河床和山体，相对于坝体可视作为无限域。坝体结构的地震响应是由地壳深部输入的自由场入射地震波和由于河谷地基及坝体存在而产生的外行散射波双重作用的结果。外行散射波在向山体和河床深部传播过程中，由于几何扩散和地基内部阻尼作用，将有部分外行散射波地震动能量耗散到远域地基中，远域地基这种对大坝体系动力响应的限制起到了相当于阻尼的作用，称为“辐射阻尼”效应［1］。

对于深厚覆盖层上的土石坝，当覆盖层厚度相对坝高较大时，大坝动力分析中宜将覆盖层地基截断，只取临近坝体部分覆盖层作为大坝结构的近域地基，连同坝体一起作为计算分析对象。目前，对截断边界的处理方式主要是做人工固定，使得外行散射波无法透过模型边界向远域地基扩散，而被全部反射回模型内部，远域地基的“辐射阻尼”效应无从体现，从而显著增加大坝结构的动力响应水平。加之，覆盖层材料相对基岩较软弱，截断边界内外土体材料特性接近，固定边界条件的这一效应相对基岩上大坝更加显著。可以通过在截断边界上施加各种人工边界条件的方法，来消除或降低由地基截断边界所带来的计算误差。

人工边界条件大体可以分为时空耦联的全局人工边界条件和时空解耦的局部人工边界条件［2］。局部人工边界条件虽然不能像全局人工边界条件那样对无限域介质实现精确模拟，但是其和现有计算方法容易结合、操作简便，得到了广泛的实际应用。透射边界、黏性边界和黏弹性边界是当前结构动力分析中应用较广的几种局部人工边界条件：模拟波在人工边界上穿过的过程、以有限区域模拟波向无限域传播的透射边界条件［3］，通过多次透射处理可以使得计算结果达到比较高的精度；黏性边界条件通过于边界上设置黏性阻尼器来吸收广义结构传向地基的波动能量［4］，具有施加简便且适用性强的特点；黏弹性边界条件通过在地基截断边界上同时施加黏性阻尼器和线性弹簧复合力学元件，吸收外行波能量和模拟远域介质的弹性恢复能［5-8］。黏弹性边界克服了黏性边界不能模拟半无限地基的弹性恢复性能、可能出现低频漂移的问题，且较透射边界更容易操作，有良好的数值稳定性，已在结构-地基动力相互作用相关问题研究中得到广泛应用［9］。

本文，将黏弹性边界条件引入到深厚覆盖层上土石坝动力分析中，用以反映覆盖层远域地基对耗散地震动能量作用的“辐射阻尼”效应和弹性恢复性能。通过采用施加等效地震惯性力的方法解决黏弹性边界条件下深厚覆盖层上土石坝动力分析的地震动输入问题，同时利用等效线性化分析方法反映覆盖层地基边界上黏弹性边界条件的动力非线性特性，建立了基于黏弹性边界条件的深厚覆盖层上土石坝动力反应分析方法，研究边界条件对深厚覆盖层上土石坝动力反应分析结果的影响规律。

2 基于黏弹性边界条件的土石坝动力分析方法

2.1 黏弹性人工边界条件由弹性介质中二维出平面剪切柱面波运动方程和材料应力应变关系，可以确定圆柱任一半径rb处剪应力与质点位移和振动速度间的关系［6］：

u(rb，t)为切向位移；vs为剪切波速，为剪切模量。

如果将无限域地基在半径rb处截断，同时施加一阻尼系数cs=ρvs的阻尼器，再并联上一刚度系数为Ks=G/( )

2rb的线性弹簧，则质点的平衡状态不变且可消除波在人工截断边界上的反射，模拟剪切波由结构-地基系统内向边界外无限域地基透射传播［6］。同理，为了模拟压缩纵波在边界上的透射过程，可以在边界面法线方向上施加阻尼器与弹簧并联组成的复合物理元件，对于线性弹簧刚度系数KT和阻尼器黏滞系数cT，可将式（1）中的G和vs直接用E和vp替换即可［6］。基于球面波动方程，则可以将黏弹性人工边界条件推广到三维情形［7-8］。黏弹性边界条件的物理模型，如图1所示。

图1 黏弹性边界条件物理模型

在基于黏弹性边界条件的近场地基和结构体系有限元动力分析中，人工边界结点的运动可用施加应力人工边界的有限元运动方程模拟，边界结点反应与内部有限元结点反应采用相同的差分格式计算，人工边界结点的计算稳定性条件与内部有限元结点相同［9］。

2.2 等效惯性力地震动输入方法黏弹性人工边界条件实现的关键问题之一是解决地震动输入问题。黏弹性边界条件下，相对于单一震源的内源激励问题，地震等外源激励问题的地震动输入较固定边界条件变得困难。目前，普遍采用的方法是在边界结点上输入应力波或位移和速度时程［10］，具体就是将输入地震波转化为直接作用于人工边界结点上的等效荷载，以此来实现地震动的输入。已有研究成果表明，这种在边界结点上施加用结点位移和速度来表达的集中力荷载、实现地震动输入的方法通常情况下效果较为理想。但是，在目前的土石坝动力分析中，地震动的输入普遍是采用施加等效地震惯性力的方式，是用内部结点的振动分析来近似模拟地震波在结构内部传播而引起的波动反应，而非真正意义上的波动分析［11-13］。有研究者分析了结构动力分析边界位移型地震动输入方式和内部输入地震惯性力地震动输入方式在土工结构动力分析中的适用性问题［13］。普遍的认识是，在当前地震地面运动信息主要来自加速度记录的情况下，在一致地震动输入时，宜采用加速度输入模式，应慎重对待地震位移输入模式［13］。

对于外源激励的地震问题，可以近似为多质点振动的内源激励问题，即认为地震对结构的作用等价于在结构内部所有结点上同时作用一条相同的地震加速度时程，采用施加等效地震惯性力的方法，同时在边界结点和内部结点上施加地震加速度，用以反映地震对结构的作用。此时，施加了黏弹性边界的地基-结构体系动力平衡有限元方程为，

采用结点惯性力的地震动输入方式，施加了黏弹性边界条件的结构动力平衡有限元方程除增加了由边界结点上弹簧和阻尼器所产生的附加刚度阵和阻尼阵外，和以往固定边界条件土石坝动力反应分析动力平衡有限元方程相比没有变化，可以在已有固定边界条件显式差分格式基础上进行调整（详见后文述），即可实现施加了黏弹性边界条件的有限元方程求解。这样，一方面省去了位移法输入中，将边界结点位移和速度转化为结点集中力的繁琐［10］，另一方面更容易与现有有限元计算程序相结合，程序的开发具有延续性。

相比于边界结点上位移、速度型的外源地震动输入方式，内源型等效地震惯性力的输入方式在物理概念上是有一定近似的，并不是严格的波动分析。具体表现有：结构内部结点的加速度、位移和速度时程不能表现出相对于边界结点在时间上的延迟；对于施加了人工边界条件的情况，边界结点的运动情况也不会像边界等效荷载方法那样十分精确。但总体来讲，这些差异或近似对结构整体动力分析结果的影响并不大。再考虑到地震惯性力输入方式应用的具体经验和对已有研究成果继承、延续，可以认为采用多质点内源激励法（施加等效地震惯性力）的地震动输入方式，实现黏弹性人工边界条件下深厚覆盖层上土石坝动力分析地震动输入是合理的。

2.3 对土体动力非线性特性的考虑目前，大多数的黏弹性边界条件研究都是将远域地基做线弹性介质考虑，地基的动模量为固定值，即黏弹性边界条件模型也是线性的。对于岩石地基，可以认为这样处理影响不大；但是，对于深厚覆盖层上的土石坝工程，不考虑边界上覆盖层土体动力变形的非线性特性将会给计算带来较大误差［14-15］。可以采用和内部土体相同的处理方式，即用等价线性化方法来反映边界土体动力变形的非线性特性：黏弹性边界条件中，土体材料动变形特性参数都是和土体动剪模量G直接相关或间接相关的量，而土体动剪模量随剪应变γ变化的非线性特性，满足以下关系，

式中：Gmax为土的最大动剪模量；γc为参考剪应变。

所以，在具体的数值计算中，黏弹性边界条件中应变-模量的迭代模式和内部土体单元相同，可以采用和内部土体一样的方式来考虑边界物理模型动力变形的非线性——等价线性化模式，而不必做格外的特殊处理。通过考察临近边界内部土体单元的剪应变幅值，确定土体单元动剪模量，进而确定边界结点黏弹性边界条件特征参数。

对于施加了黏弹性边界条件的深厚覆盖层上土石坝-地基系统的动力反应计算，可以通过采用施加等效地震惯性力的方法实现黏弹性边界条件下深厚覆盖层上土石坝动力分析的地震动输入，同时利用等效线性化分析方法反映覆盖层地基边界上黏弹性边界条件的动力非线性特性。施加了黏弹性边界条件的结构动力反应计算流程和迭代模式和固定边界条件的相同［12］。

3 基于黏弹性边界条件的土石坝动力反应有限元求解方法

黏弹性边界条件下，结构动力平衡有限元方程相对于固定边界条件，增加了附加阻尼矩阵和刚度矩阵，需重新推导有限元平衡方程显式差分求解格式。以下，在固定边界条件结构动力有限元平衡方程Wilson-θ法求解显式差分格式的基础上［12］，推导施加了黏弹性边界条件后的结构动力平衡有限元方程求解显式差分格式。结构动力平衡有限元方程为，

对于施加了黏弹性边界条件的结构体系，

所以，施加了黏弹性边界条件的结构体系动力平衡有限元方程为，

设τ=θ·Δt（θ一般取1.4），假定在t～t+τ时段内，加速度按线性关系变化。则有，

在t+τ时刻有，

将式（8）和式（9）代入式（10），再经过一系列复杂的整理、变换，可以得到如下平衡方程式，

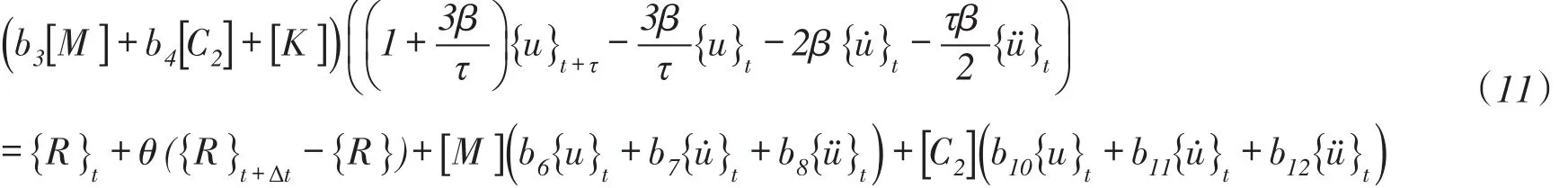
b=2+τb，b=1+bβ，b=3b，b=2b，b=τb。

8259410τ91191229

设特征刚度矩阵，

设特征位移向量，

设特征荷载向量，

可以得到如下特征方程，

在基于黏弹性边界条件的大坝动力反应有限元计算中，需要将大坝模型结点区分为内部结点和边界结点两类，同时单元也划分为内部单元和边界单元。对于二维问题，还要将边界结点和单元按底边界、左侧边界和右侧边界区分开来。图2为施加了黏弹性边界条件的深厚覆盖层上土石坝动力反应分析有限元计算模型示例。

4 边界条件对深厚覆盖层上土石坝地震动力反应分析结果的影响

4.1 计算程序基于前述计算方法，在固定边界条件土石坝动力反应分析有限元程序的基础上，开发了施加能够模拟地震波透过截断边界、反映远域地基耗散外行散射波能量性能和远域地基弹性恢复性能的黏弹性边界条件有限元程序，进行深厚覆盖层上土石坝地震动力反应分析的边界条件影响规律研究（以固定边界和黏弹性边界为例）。程序计算中需要输入的信息包括：模型的网格信息（要区分内部结点和不同边界线上的结点，区分内部单元和不同边界线上的单元）、地震动加速度时程、土体基本物理特性参数和动力变形特性参数，以及相关计算控制参数等。

4.2 计算模型和参数以深厚覆盖层上简单心墙堆石坝模型为例，进行大坝在黏弹性边界条件下的动力反应分析，并与固定边界条件下的计算结果进行对比。模型坝高30m，分别取1倍坝高的覆盖层厚度和深度作为坝体的近域地基。计算模型网格剖分和图2相同，包含254个单元和294个结点，其中包括218个内部单元和36个边界单元，包括257个内部结点和37个边界结点。土体材料动力变形特性参数，如表1和表2。输入地震波取某实际工程场地波，将水平向输入峰值加速度调整为0.1g和0.3g，竖直向加速度水平取为水平向的2/3，水平向输入归一化加速度时程如图3所示。

图3 归一化的输入地震动加速度时程

表1 土体动力变形特性参数

表2 土体动剪模量比GGmax和阻尼比λ衰减（增长）的数值化结果（以百分数计）

表2 土体动剪模量比GGmax和阻尼比λ衰减（增长）的数值化结果（以百分数计）

γ G Gmaxλ坝体和地基心墙坝体和地基心墙0.0001 85 95 7.0 12.0 0.0005 59 70 17.0 18.0 0.001 40 53 21.8 22.0 0.002 25 37 24.8 24.0 0.003 19 28 26.8 25.0 0.004 15 25 27.8 25.5 0.005 14 24 28.0 25.7 0.01 12 21 28.2 26.0

4.3 计算结果与分析图4是两种边界条件下，坝体和地基内部加速度放大倍数分布的对比。从图中可以看出，两种边界条件下，坝体内部加速度放大倍数分布规律基本相同：随着高程的增加，加速度放大倍数逐渐增加，在坝顶处达到最大；在输入加速度水平相对较低的地震动（0.1g）作用下，坝坡表面没有像高幅值（0.3g）那样出现放大现象。但是总体上看，黏弹性边界条件下坝体的加速度反应水平相对固定边界条件大幅降低。水平向输入加速度峰值为0.1g时，图5是两种边界条件下，坝体竖向中心线上底边界结点和坝顶结点振动加速度时程曲线的对比；图6是两种边界条件下，坝体竖向中心线上底边界结点和坝顶结点振动绝对加速度反应谱曲线对比。

从图5可以看出，虽然黏弹性边界施加等效地震惯性力的地震动输入方式，不能在边界结点上实现绝对精确的加速度时程输入，但是从计算结果来看，底边界中心结点的加速度反应时程和固定边界的加速度输入时程基本相同，即和预设输入地震动基本相同：固定边界水平向加速度峰值为0.1g输入时，黏弹性边界的底边界结点加速度反应的极值为0.098g，两者很接近，而且从波形上看也是基本相同的，除两侧边界的顶端结点由于处在地表，反应和固定边界输入有小幅差异外，其它边界结点的反应和预设地震动输入都基本相同。所以，施加等效地震惯性力的地震动输入方式虽然没有边界上位移、速度型输入方式在理论上那么严谨，但是效果却很好，施加地震惯性力的地震动输入方式在基于黏弹性人工边界条件的深厚覆盖层上土石坝动力反应分析中是可行的。

从坝体竖向中心线上坝顶结点加速度反应时程曲线可以看出，两种边界条件下坝顶点的加速度反应时程曲线波形基本形同，但是反应的水平差别很大：固定边界条件下求得加速度峰值为0.351g，而黏弹性边界条件下求得加速度峰值为0.223g，较固定边界条件低36.5%，可见固定边界条件的边界处理方式，大幅提升了大坝坝体的加速度反应水平。

图4 固定边界和黏弹性边界条件下水平向加速度放大倍数在坝体和地基内分布的对比

图5 固定边界和黏弹性边界条件下结点水平向振动加速度时程对比

从图6可以看出，黏弹性边界条件下边界结点的加速度反应水平和固定边界输入基本相同，地震动加速度反应谱谱形也看不出明显差别。坝顶处，虽然两种边界条件下加速度反应的水平差异较大，但是加速度反应谱的谱形很接近，坝顶处的加速度反应相对输入地震动，反应谱的极值点都向长周期方向移动。

综上，黏弹性边界条件的施加使得坝体和地基的地震动力反应水平降低，但对结点振动加速度反应谱的谱形没有明显影响，即以往的固定边界条件使得加速度反应计算的结果偏大，但是结构体系的振动特性没有明显改变，而仅限于量值水平的提升。所以，结合加速度反应的量值水平和在坝体和地基内的分布规律来看，以往固定边界条件下得到的大坝加速度反应虽然在量值上偏大，但一般定性规律应当是准确的。

图6 固定边界和黏弹性边界条件下水平向结点振动绝对加速度反应谱对比

5 结论

本文针对深厚覆盖层上土石坝动力分析边界处理方法问题，将黏弹性边界条件引入到深厚覆盖层上土石坝动力反应分析中，用以反映覆盖层远域地基的“辐射阻尼”效应和弹性恢复性能。采用施加等效地震惯性力的方法解决了黏弹性边界条件下深厚覆盖层上土石坝动力分析的地震动输入问题，同时采用等效线性化方法反映覆盖层地基截断边界上黏弹性边界条件的非线性特性，建立了基于黏弹性边界条件的深厚覆盖层上土石坝动力反应分析方法，并初步探讨了边界条件（以固定边界和黏弹性边界为例）对深厚覆盖层上土石坝地震动力反应分析结果的影响规律。主要研究结论为：

（1）采用等效线性化方法可以反映覆盖层地基截断边界上黏弹性边界条件的非线性特性，施加等效地震惯性力的方法可简单而有效解决黏弹性边界条件下土石坝动力分析地震动输入问题，且精度满足要求；

（2）基于黏弹性边界条件的土石坝动力反应分析计算结果表明，固定边界条件大幅提高了坝体在地震作用下的响应水平，使得计算的结果偏于安全；

（3）加速度反应谱分析表明，边界条件对深厚覆盖层上土石坝地震动力反应分析计算结果的影响只限于加速度反应的量值水平，而对坝体和地基的振动特性不产生明显影响，加速度反应在坝体内部的分布规律基本不受边界条件的影响。

这里需要指出的是，本文的主要研究目的是探索建立深厚覆盖层上土石坝动力分析黏弹性边界处理新方法，文中的主要计算分析内容属探索性的定性对比分析。所以，对于计算模型的建立及其有限元网格划分、材料特性参数的选取和输入地震动等部分细节内容，存在部分的理想化假定，并不是很完善，仍有值得进一步深入探讨的地方，例如黏弹性边界处理方式下深厚覆盖层近域地基合理范围的确定等。但是，从验证方法合理性以及一般性规律探索的定性分析角度看，本文的研究结论是可以信赖的。

［1］ 陈厚群.坝址地震动输入机制探讨［J］.水利学报，2006，37（12）：1417-1423.

［2］ 杜修力，赵密，王进廷.近场波动模拟的人工应力边界条件［J］.力学学报，2006，38（1）：49-56.

［3］ LIAO ZP，WONG H L.A transmitting boundary fornumerical simulation ofelastic wave propagation［J］.Soil Dynamicsand Earthquake Engineering.1984，3（4）：174-183.

［4］ LYSMER J，KUHLEMEYERR L.Finite dynamicmodelforinfinitemedia［J］.Journal ofengineeringmechanics division.ASCE.1969，95（4）：759-877.

［5］ DEEKSA J，RANDOLPH M F.Axisymmetric time-domain transmitting boundaries［J］.Journal ofEngineering Mechanics.ASCE.1994，120（1）：25-42.

［6］ 刘晶波，吕彦东.结构-地基动力相互作用问题分析的一种直接方法［J］.土木工程学报，1998，31（3）：55-64.

［7］ 刘晶波，王振宇，张克峰，等.考虑土-结构相互作用大型动力机器基础三维有限元分析［J］.工程力学，2002，19（3）：34-38.

［8］ 刘晶波，王振宇，杜修力，等.波动问题中的三维时域黏弹性人工边界［J］.工程力学，2005，22（6）：46-51.

［9］ 王立涛，陈厚群，马怀发.人工黏弹性边界的接触非线性问题在FEPG中的实现［J］.水力发电学报，2009，28（5）：179-181.

［10］ 马怀发，王立涛，陈厚群.粘弹性人工边界的虚位移原理［J］.工程力学，2013，30（1）：168-174.

［11］ IDRISS IM，LYEMER J，HWANG R，etal.QUAD-4：a computerprogram forevaluating the seismic response ofsoil structures by variable damping finite elementprocedures［R］.Berkeley：University ofCalifornia，Berkeley.1973.

［12］ 刘颖，谢君斐.砂土震动液化［M］.北京：地震出版社，1984.

［13］ 楼梦麟，李强.关于结构系统地震输入模式问题的讨论［J］.世界地震工程，2004，24（2）：21-25.

［14］ 尚守平，卢华喜.土波动问题中基于动模量衰减的人工边界［J］.湖南大学学报，2005，32（6）：18-23.

［15］ 卢华喜，梁平英，尚守平.地基非线性波动问题中黏-弹性人工边界研究［J］.岩土力学，2008，21（4）：1911-1916.

Visco-elastic boundary processing method for dynamic analysis of earth-rock filldam on deepoverburden layer

YANG Zhengquan1，2，3，LIU Xiaosheng1，2，3，WANG Xiaogang1，2，3，ZHAO Jianming1，2，3，WEN Yanfeng1，2，3
（1.State Key Laboratory ofSimulation and Regulation ofWaterCycle in RiverBasin，Beijing 100038，China；2.Dept.ofGeotechnicalEngineering，IWHR，Beijing 100048，China；3.Engineering Research Centeron Anti-Earthquakeand Emergency Support TechniquesofHydropowerProjects，Ministry ofWaterResource，Beijing 100048，China）

In the dynamic analysis of earth-rock fill dam on deep overburden layer，the foundation of dam is truncated usually when the depth of overburden layer is higher than the height of dam on it，and the analysis object is the system of dam and its near-field foundation.The problem that dam response becomes larger because of the boundary truncation can be solved effectively though the application of visco-elastic boundary condition in dynamic analysis of the dam-foundation system.Dynamic response analysis method of the earth-rock fill dam on deep overburden layer base on visco-elastic boundary condition is established in the paper.The problem of seismic motion input under visco-elastic boundary condition is solved by the method of applying equivalent seismic inertia force on structures.Dynamic nonlinear characteristics of soil is reflected using the equivalent linearization method.The results show that，the problem of seismic motion input under visco-elastic boundary condition can be solved effectively by the method of applying equivalent seismic inertia force on structures，and the dynamic response levels of dam in earthquake is increased when the cut-off boundary of dam is fixed，which makes the calculated results conservative.

deep overburden layer；earth-rock fill dam；dynamic analysis；boundary processing method；visco-elastic boundary

TV641

A

10.13244/j.cnki.jiwhr.2017.03.006

1672-3031（2017）03-0200-09

（责任编辑：杨 虹）

2016-08-01

国家自然科学基金项目（51509272，51679264）；中国水科院基本科研业务费项目（GE01458292017）；国家重点基础研究发展计划暨973计划课题（2013CB036404）；“十二·五”国家科技支撑计划课题（2013BAB06B02）；水利部公益性行业科研专项项目（201501035）

杨正权（1980-），男，吉林集安人，博士，高级工程师，主要从事土动力学及土工结构抗震研究。E-mail：yangzhq@iwhr.com