基于ABAQUS的海冰单元开发及冰载荷直接计算法

龚榆峰，张正艺，2，3，刘敬喜，2，3，董问，解德，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2船舶和海洋水动力湖北省重点实验室，湖北武汉430074

3高新船舶与深海开发装备协同创新中心，上海200240

基于ABAQUS的海冰单元开发及冰载荷直接计算法

龚榆峰1，张正艺1，2，3，刘敬喜1，2，3，董问1，解德1，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2船舶和海洋水动力湖北省重点实验室，湖北武汉430074

3高新船舶与深海开发装备协同创新中心，上海200240

［目的］随着全球气温的不断升高，北极冰层逐渐融化，开发利用北极航线和北极资源受到国际社会的广泛关注，各国掀起了新一轮的极地船舶建造高潮，而在极地船舶的设计过程中，如何确定船舶冰载荷显得尤为重要。近年来，采用数值方法计算极地结构受到的冰载荷逐渐成为国内外学者关注的重点，而目前的通用商业有限元软件中缺少特定用于模拟海冰力学特性的相关海冰单元，为相关数值研究工作的开展增加了困难。针对这一问题，［方法］结合Reinicke和Remer提出的各向同性海冰失效准则，在ABAQUS二次开发平台UEL上开发用于模拟海冰失效的新型单元。在所开发的单元中引入弹性基础用以模拟浮力和重力的作用。采用典型的斜坡和圆锥结构算例并结合相关规范公式对所开发的新型单元进行验证。［结果］对比二者之间的计算结果发现，直接计算法与规范公式的计算结果吻合较好。［结论］所提出的直接计算法能够为冰区结构设计提供工具和一定的参考。

冰载荷；直接计算法；ABAQUS；沙漏控制；自定义单元

0 引 言

随着全球气温的升高，北极地区的海冰逐渐融化，人类对极地船舶与海洋结构物的需求也随之增加。在进行极地船舶与海洋结构物的设计时，如何合理、有效确定结构物与海冰相互作用过程中受到的冰力，是一个长期被国内外相关研究人员关注的问题。然而海冰与结构物的相互作用是一个相当复杂的过程，在目前的研究中，研究人员通常将海冰与不同结构物相互作用过程中海冰的破坏模式归纳为压碎、弯折和劈裂等几类。

当海冰与斜坡或圆锥结构物作用时海冰常常会出现弯折破坏。国内外相关研究人员针对海冰与海洋结构物的弯折破坏进行了大量研究工作，其中 Bercha和 Danys［1］，Croasdale等［2］将冰排理想化为放置于弹性基础上的线弹性板，从而提出了计算冰排和斜坡、圆锥结构相互作用时冰力大小的理论公式。Ralston［3］则基于塑性上限理论提出了计算冰排和圆锥结构相互作用时冰力大小的理论公式。李峰等［4］采用弹性基础梁理论分析了冰与斜面结构作用时的弯曲破坏。法国船级社（Bureau Veritas，BV）公布的针对船舶和海洋结构物上冰力大小的计算指南（BV_565NI）［5］和美国石油协会（American Petroleum Institute，API）公布的规范API-RP-2N［6］中将海冰理想化为作用于弹性基础上的线弹性材料，提出了用于计算冰排和斜坡、圆锥结构相互作用时冰力大小的相关公式。

对于海冰弯折破坏的数值计算研究，Sand和Horrigmoe［7］，Derradji-Aouat［8］等采用商用有限元软件ANASYS计算了冰排与斜坡结构相互作用时结构受到的冰力，在其研究中冰排被理想化为作用于弹性或弹塑性基础上的线弹性板。黄焱等［9］在LS-DYNA中模拟了圆环形冰排弯曲破坏以及冰排与锥体结构相互作用的过程。宋安等［10］采用缩尺的冰模型试验研究了冰排作用于斜面结构时的冰力大小，并将结果同相关理论公式进行了对比。

综上所述，国内外研究人员已对冰排与固定倾斜结构作用时结构受到的冰载荷进行了大量的理论、试验和数值研究。然而在已开展的冰排与固定倾斜结构作用时冰载荷的数值研究中，海冰本构关系的模拟大多基于商业有限元软件已有的材料模型和失效准则，使得难以对海冰的力学特性进行合理描述。为了更好地评估冰排与固定倾斜结构作用时结构受到的冰载荷，应在数值分析中引入适用于模拟海冰力学特性的特定材料模型和失效准则。因此，进一步开展冰排与固定倾斜结构作用时的冰载荷直接计算法研究，并基于现有商业有限元软件开发具有一定通用性的海冰单元以描述海冰的力学行为与考虑浮力的作用很有必要，这将进一步提高采用直接计算法确定结构冰载荷的效率，并使得所编制的程序具有一定的通用性，具有一定的工程实践意义。

本文将基于通用商业有限元软件ABAQUS的自定义单元子程序创建集成了Reinicke和Remer［11］提出的各向同性海冰失效准则和弹性基础的8节点六面体单元用于模拟海冰。同时为了对所开发的单元进行验证，将采用开发的单元计算冰排与斜坡结构相互作用过程中的冰力大小，并将所获得的计算结果与BV和API给出的相关规范公式进行对比。

1 单元及失效准则介绍

1.1 所开发单元基本原理

8节点六面体缩减积分单元示意图如图1所示。

图1 单元示意图Fig.1 Schematic of element

根据有限元理论［12］，单元内任意一点的位移u可以表示为

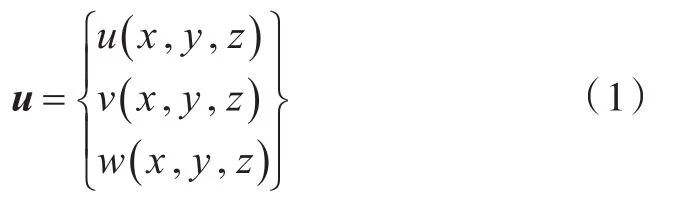
式中：u，v，w为沿坐标轴x，y，z轴的位移分量；x，y，z为总体坐标系的3个坐标轴。单元内任意一点的位移u可以由单元的形函数和单元各个节点的位移来表示：

式中：Na为基于节点位置事先给定的函数，又称单元的形函数；ua为单元内各个节点的位移。

单元任意一点的应变可用引起应变的3个分量来表示：

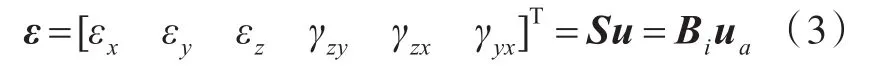
式中：S为单元应力矩阵；Bi为单元应变矩阵。

所以Bi可以由式（4）给出。

根据应力—应变关系，采用矩阵D可以将单元中的6个应力分量和6个应变分量联系起来，单元中应力σ可以表示为

最后，由虚功原理可以得到单元刚度矩阵K，

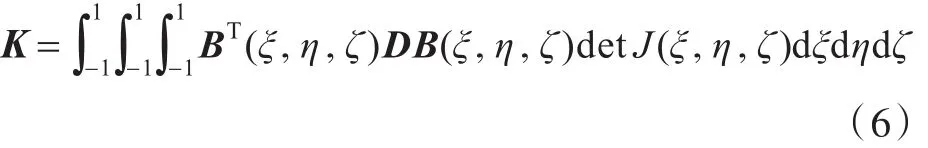
式中，J为雅克比行列式。采用高斯积分时，式（6）可以简化为

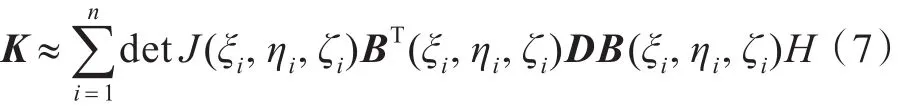
式中，H为权函数。由于本文所开发的单元为完全缩减积分单元，只有一个积分点，即式（7）中i=1。对应的积分点在局部坐标系下的坐标为（0，0，0），即式（7）中ξi=0，ηi=0，ζi=0，对应于积分点数量的权函数H=8.0。

为了考虑海冰受到的浮力，在单元中引入弹性基础用于考虑海冰的浮力作用。弹性基础反力R与单元底部节点的垂向位移w和弹性基础中弹簧的刚度ks之间的关系如下［13］：

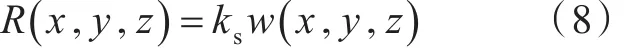
由节点力平衡方程可以得到弹性基础反力和垂向位移之间的关系：

式中，K0为考虑弹性基础而引入的单元刚度附加矩阵。

最后，可以得到引入弹性基础后的单元平衡方程：

式中，Ke为不考虑弹性基础时的单元刚度矩阵。

1.2 Reinicke和Remer各向同性海冰失效准则

Reinicke和 Remer［11］在总结前人研究的基础上提出了用于描述各向同性海冰失效行为的失效准则。

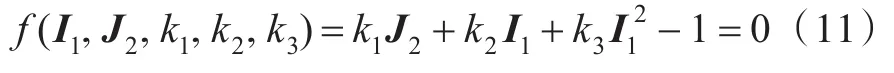
式中：k1，k2和k3为材料常数，通过试验确定；I1为应力张量第1不变量；J2为应力偏量第2不变量。当f(I1，J2，k1，k2，k3)=0 时，材料失效。失效后的材料弹性模量和泊松比分别变为Ec=60 MPa，vc=0.33。本文中使用的材料常数的取值参考文献［9］中由模型试验拟合得到的结果，k1=0.674（MPa）-2，k2=0.853（MPa）-1，k3=0.014（MPa）-2。

1.3 沙漏控制

本文采用哑单元方法并结合ABAQUS用户自定义输出变量子程序UVARM来引入单元的沙漏控制，实现所开发单元的结果可视化。哑单元是指与所开发单元使用相同节点的一组C3D8R实体单元，其弹性模量定义为一个非常小的值，如1.0×10-20Pa，同时可以在哑单元中直接定义单元的沙漏刚度，从而引入单元沙漏控制。通过UVARM子程序，将所开发单元的应力、应变和损伤变量等单元状态变量赋值给哑单元上的自定义输出变量，从而可以在ABAQUS后处理中实现计算结果的可视化。具体流程如图2所示。

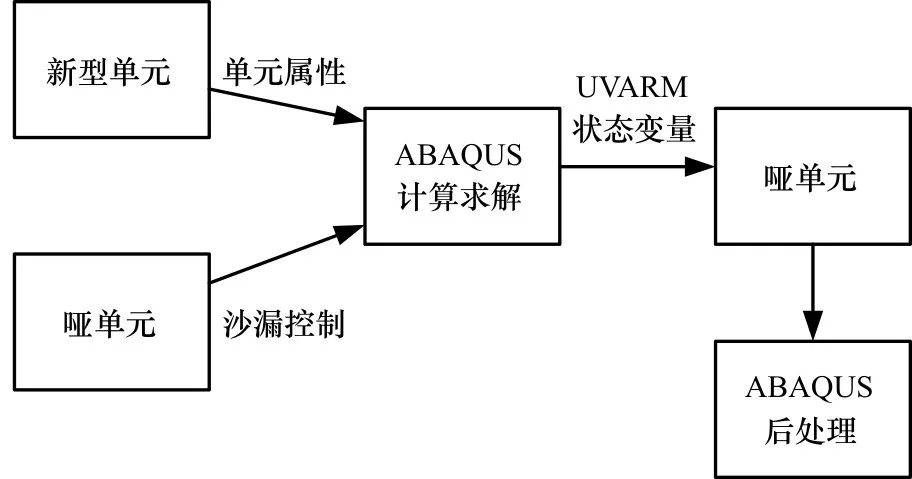
图2 单元计算流程图Fig.2 Flow chart of element computation

2 算例验证

为了验证所开发的单元，首先采用所开发的单元模拟正方体冰体单轴拉伸和压缩情况，将计算得到的单元应力—应变关系与解析解结果进行对比。而后，采用所开发的单元计算3组算例：端部受垂向载荷的半无限长冰梁、半无限大冰排与斜坡结构、锥台结构的相互作用。并将计算结果与 BV［5］以及 Croasdale［14］，Ralston［3］给出的建议公式进行比较，其中BV给出的一端受垂向载荷作用的半无限长冰排能承受的最大外力F的计算公式如式（12）所示，半无限长冰排失效位置计算公式如式（13）所示。计算中采用的材料参数及Reinicke和Remer失效准则参数如表1所示。

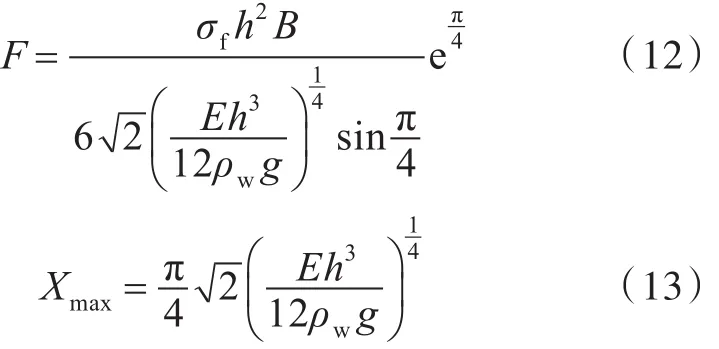
式中：B为冰排的宽度；h为冰排的厚度；σf为冰排的拉伸强度；E为冰排的弹性模量；ρw为海水的密度；g为重力加速度。

表1 计算中使用材料参数Table 1 The material constants used in the simulation

2.1 单元基本特性验证

为了对所开发单元的基本特性进行验证，计算了一顶部受到强制位移、底面约束的正方体冰块的拉伸和压缩，并将计算得到的单元应力—应变关系与解析解结果进行对比。算例的示意图如图3所示。算例相关几何参数如下：模型的长度l=1 m，宽度w=1 m，厚度h=1 m。模型共有1个单元，8个节点。其中：顶部节点为5，6，7，8；底部节点为1，2，3，4。顶部节点施加z方向的强制位移；底部节点中节点1约束x，y，z方向的位移，节点2约束y，z方向的位移，节点3约束z方向的位移，节点4约束x，z方向的位移。

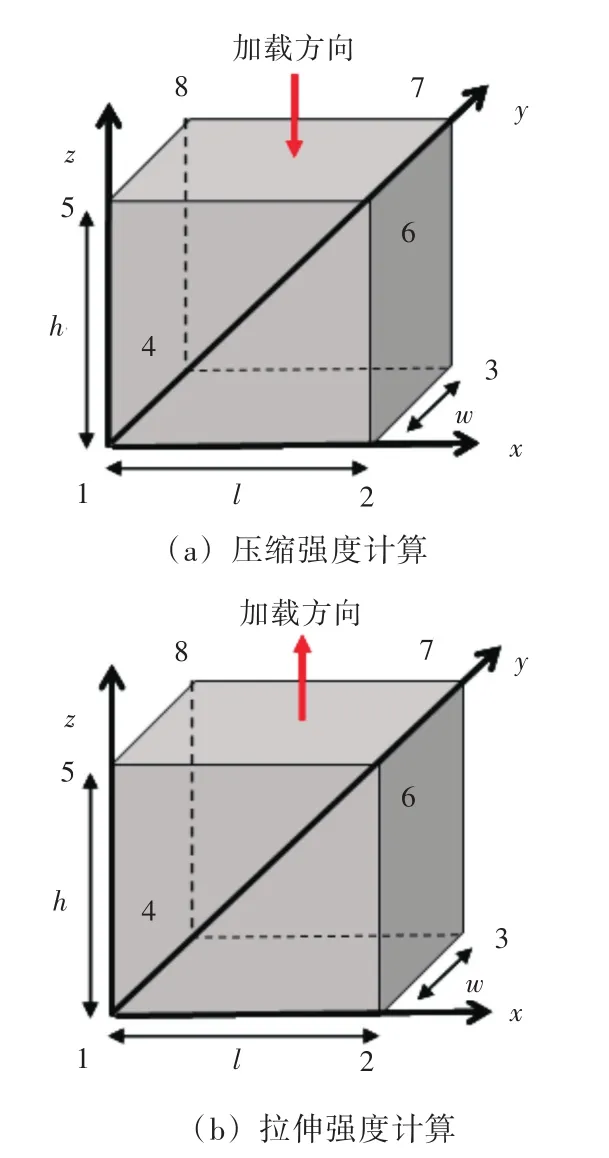
图3 正方体冰块单轴拉伸和压缩示意图Fig.3 Schematic of ice cube under uniaxial stretching and compression

使用新型单元得到的计算结果与Reinicke和Remer屈服准则解析解的对比如图4所示。将新型单元的计算结果与解析解的对比可以发现，该新型单元不仅能够描述海冰的拉伸与压缩强度不一致这一基本力学特性，而且计算得到的拉伸强度和压缩强度与Reinicke和Remer屈服准则解析解吻合很好，验证了本文提出的新型单元能够很好地实现Reinicke和Remer提出的海冰本构关系，并描述了海冰的基本力学特性。

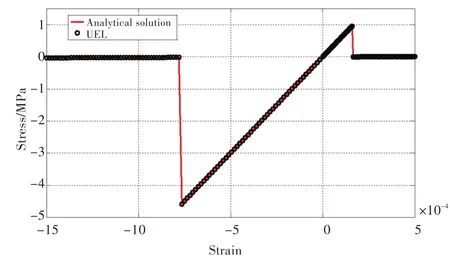
图4 应力—应变曲线计算结果对比Fig.4 Comparison of stress-strain curve

2.2 半无限长冰梁

为了验证所开发的单元，计算了半无限长冰梁在端部受到垂向位移作用时的反力，并将所得计算结果与BV给出的建议公式进行了比较。一端受垂向载荷的半无限长冰梁模型如图5所示。模型几何尺寸如下：冰梁长度l=400 m，冰梁宽度w=1 m。为了研究冰梁厚度对冰力的影响，选取了不同厚度的冰梁进行计算。冰梁的厚度分别为h=0.5，1.0，1.5，2.0，2.5和3.0 m。冰梁模型共采用2 800个新型单元和2 800个哑单元。同时，由于冰梁主要发生弯折失效，为了保证直接计算法的计算精度并描述冰梁沿厚度方向的失效发展过程，将冰梁的厚度方向划分为7个单元。模型边界条件设置为：在冰梁模型边界一端约束x，y方向的位移，另一端施加垂向的位移。

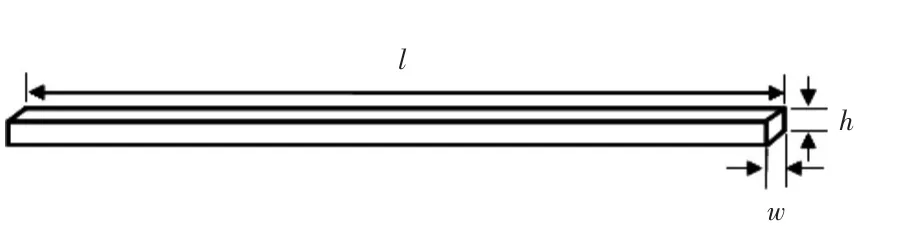
图5 半无限长冰梁示意图Fig.5 Schematic of semi-infinite ice beam

采用开发的新型单元模拟一端受垂向载荷的半无限长冰梁，得到不同时刻下厚度为0.5和3.0 m的冰梁损伤分布，如图6和图7所示。其中蓝色部分表示未损伤单元，红色表示已出现损伤的单元。从图6和图7可以看出，不同厚度的一端受到垂向载荷的半无限长冰梁其损伤发展随着厚度的不同并无明显区别。由于冰梁端部受到向下的垂直位移作用，因而冰梁在变形的过程中，上表面受到拉伸而下表面为压缩变形，由于采用的本构模型中海冰的拉伸强度要明显小于其压缩强度，所以在模型中冰梁的损伤均首先出现在上表面。而后随着端部位移的不断增加，冰梁的损伤区域由出现初始损伤的上表面逐渐沿着厚度方向，从冰梁的上表面向下表面扩展，直至整个厚度方向全部失效。同时，随着冰梁厚度的不同，冰梁出现初始损伤的位置到加载端的距离不断增加。但当冰梁出现初始失效后，随着端部位移的增加，冰梁的损伤区域不仅沿冰梁的厚度方向扩展，也会沿长度方向不断向加载端靠近。

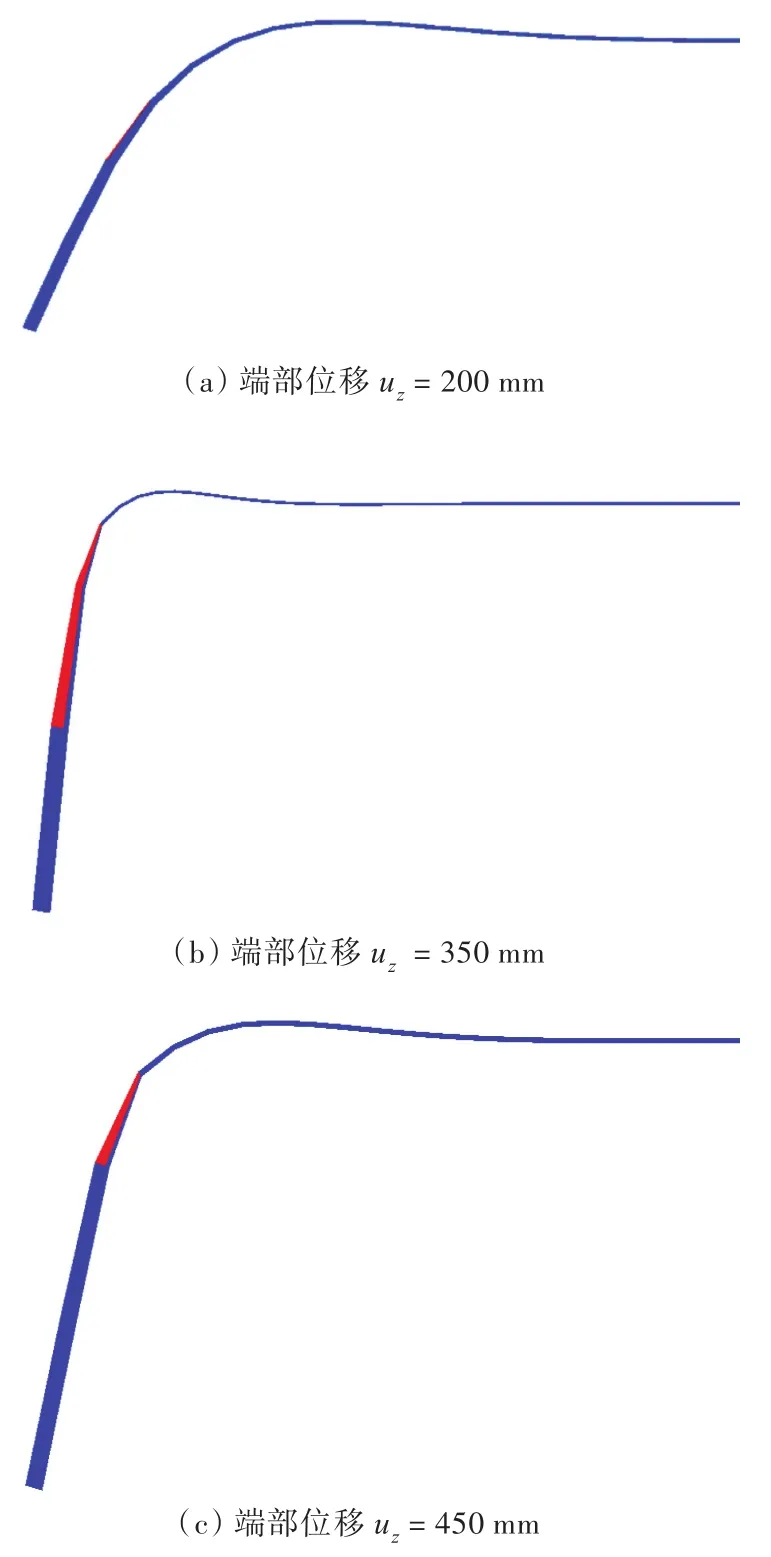
图6 厚度为0.5 m的冰梁损伤分布Fig.6 Failure process of ice beam with thickness h=0.5 m

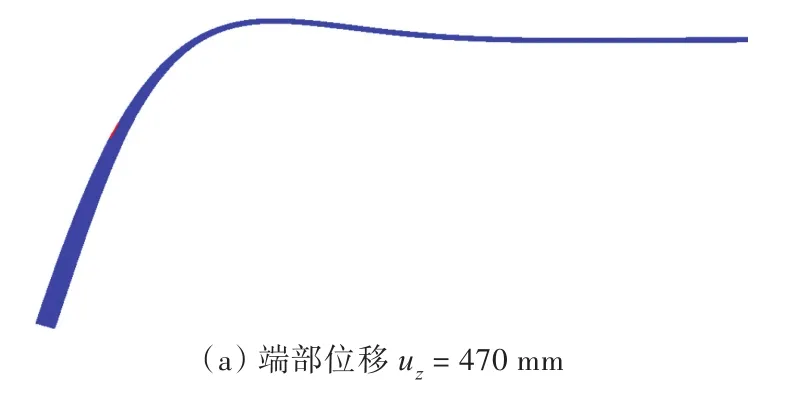
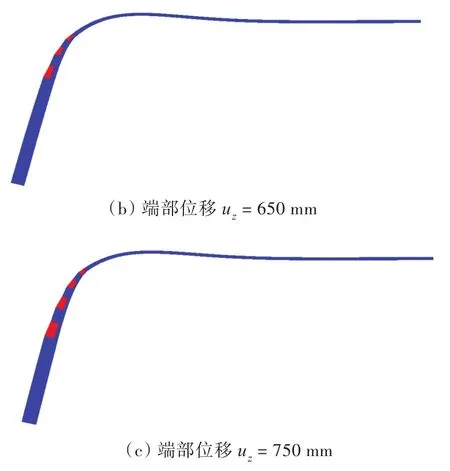
图7 厚度为3.0 m的冰梁损伤分布Fig.7 Failure process of ice beam with thickness h=3.0 m

一端受到垂向载荷的不同厚度半无限长冰梁的冰力和端部位移之间的关系曲线如图8所示。从图8中可以看出，随着垂向位移的逐渐增加，端部受到的反力也线性增加，当冰梁中的应力状态达到单元失效准则所定义的失效面时，冰梁出现失效。当单元出现失效时，直立结构受到的冰力随位移的增加出现明显的下降。但由于弹性基础的存在，以及首先出现失效的只是冰梁上表面的部分单元，冰梁并未全部失效，故仍能继续承受载荷。所以加载端部受到的反力随位移的增加，出现下降后又会再次继续上升。

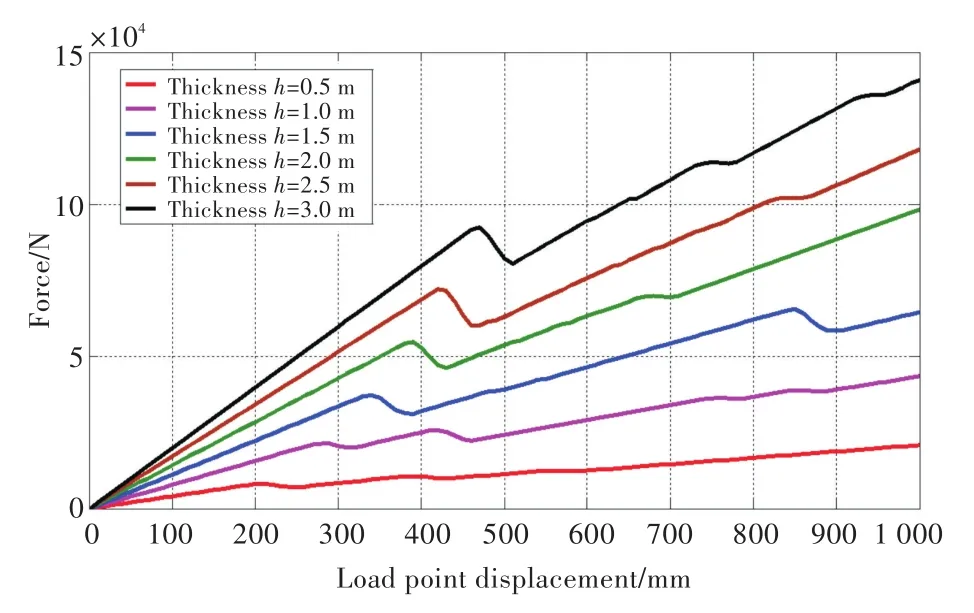
图8 不同厚度的半无限冰梁端部的反力和垂向位移关系曲线Fig.8 Vertical force-displacement curves of semi-infinite ice beam with different thickness

为了验证采用新型单元获得的计算结果，将采用直接分析法获得的冰梁出现初始失效时的失效位置、端部承受的反力与BV［5］给出的理论公式获得的解析解进行了对比，如图9和图10所示。从图中的结果对比可以看出，通过新型单元获得的失效位置和对应的端部反力与解析解吻合良好，误差仅为5%左右。说明所开发的新型单元能够准确模拟一端受垂向载荷的半无限长冰梁的弯折失效。

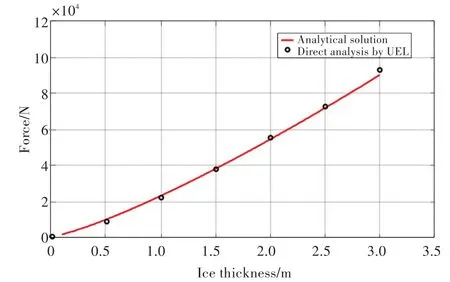
图9 直接计算法与BV公式端部反力结果对比Fig.9 Comparison of vertical force between direct analysis method and the equation presented by Bureau Veritas

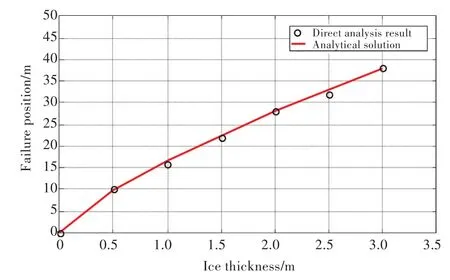
图10 直接计算法与BV公式失效位置结果对比Fig.10 Comparison of failure position between direct analysis method and the equation presented by Bureau Veritas

2.3 冰排与斜坡结构的相互作用

为了验证所开发的单元，计算了斜坡结构与冰排作用时受到的冰力，并将所得计算结果与Croasdale［14］提出的理论公式进行了对比。模型示意图如图11所示。

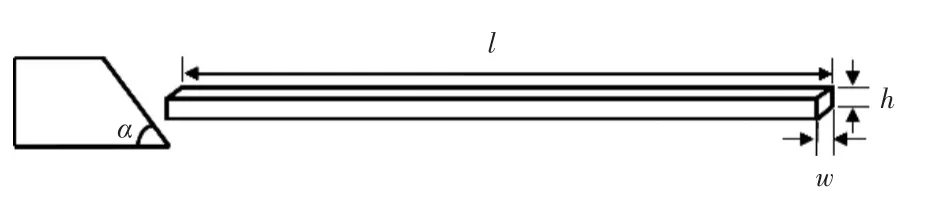
图11 斜坡结构示意图Fig.11 Schematic of sloping structure

模型几何尺寸如下：冰排长度l=400 m，冰排宽度w=1 m，冰排厚度h=3 m。为了研究斜坡结构的倾角对斜坡结构受到的冰力的影响，选取了不同倾角的斜坡结构进行计算。斜坡结构的倾角分别为α=30°，35°，40°，45°，50°，55°和 60°。冰排模型共采用2 800个新型单元和2 800个哑单元，矩形直立结构共采用6个R3D4刚体单元。模型边界条件设置为：在冰排模型边界AB上约束x，y方向的位移，其他边界不施加约束。同时直立结构的约束方式为：约束除x方向平动以外的所有自由度，同时施加x方向的平动位移。

采用开发的新型单元模拟冰排与斜坡结构的相互作用，得到不同时刻下与倾角α=30°和60°的斜坡结构作用时的冰排损伤分布图，如图12和图13所示。其中蓝色部分表示未损伤单元，红色表示已出现损伤的单元。从图12和图13中可以看出，与倾角α=30°和60°的斜坡结构作用时，冰排的损伤模式并未有明显的差别。由于冰排的拉伸强度要明显小于冰排的压缩强度，所以冰排与斜坡结构相互作用时，冰排的损伤均是首先出现在冰排受到拉伸的下表面处，然后损伤区域逐渐沿着冰排的轴向和厚度方向发展。

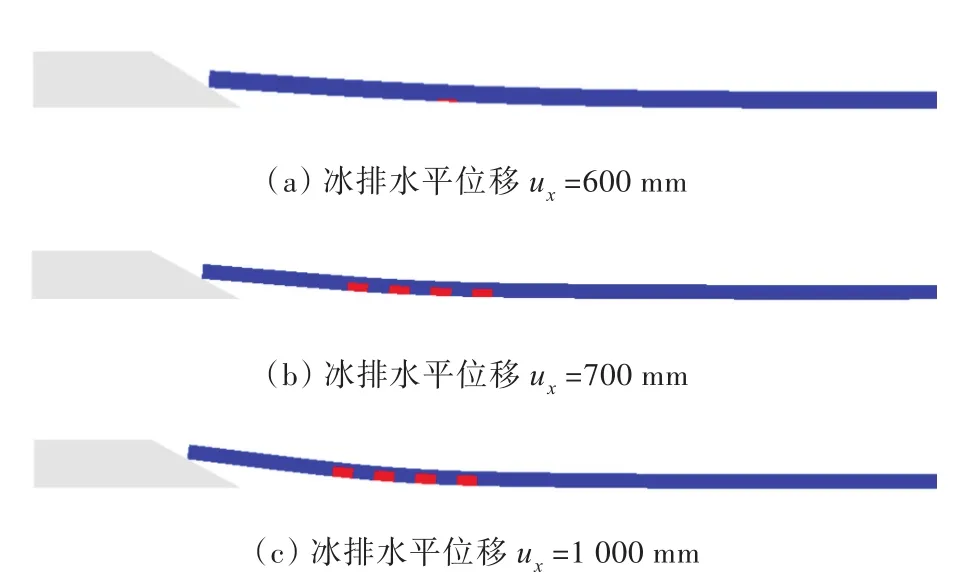
图12 斜坡结构倾角α=30°时冰排损伤分布Fig.12 Failure process of sloping structure with slope angleα=30°

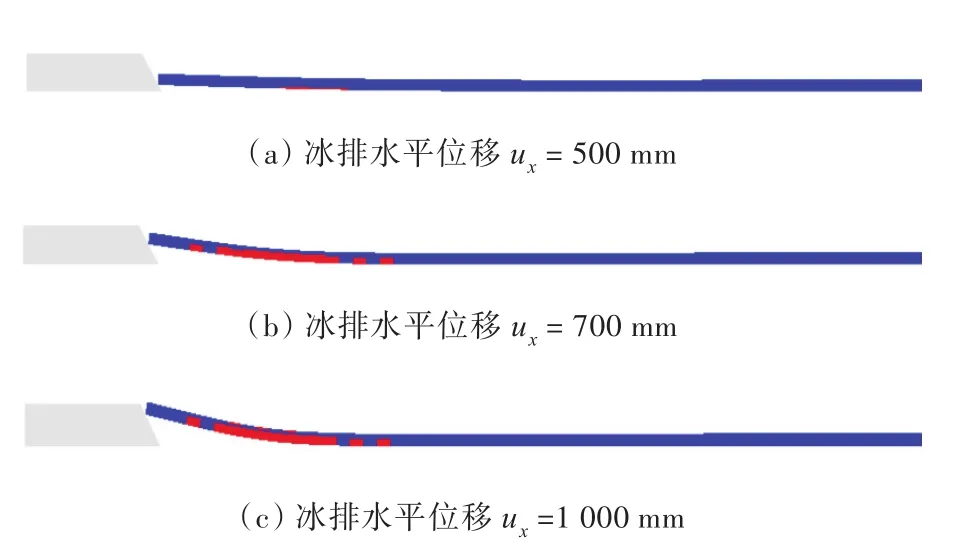
图13 斜坡结构倾角α=60°时冰排损伤分布Fig.13 Failure process of sloping structure with slope angleα=60°

冰排与不同倾角的斜坡结构作用时，斜坡结构受到的水平和垂直冰力与冰排的水平位移之间的关系如图14和图15所示。从图14和图15中可以看出，随着冰排水平位移的逐渐增加，斜坡结构受到的水平和垂直冰力也线性增加。当冰排中的应力状态达到单元失效准则所定义的失效面时，冰排出现失效。斜坡结构受到的水平和垂直冰力随冰排水平位移的增加而下降。随着冰排水平位移的继续增加，冰排沿着斜坡结构的斜面爬升，并且由于弹性基础的存在，导致斜坡结构受到的冰力再次随位移的增加而增加，使得斜坡结构的受力再次继续上升。

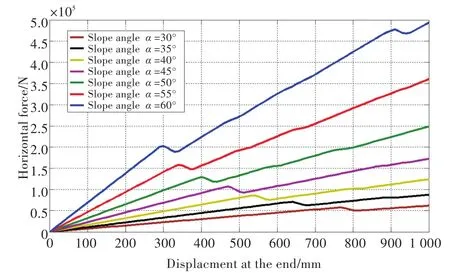
图14 斜坡结构受到的水平冰力与位移之间的关系Fig.14 Relationship between horizontal force and displacement of sloping structure

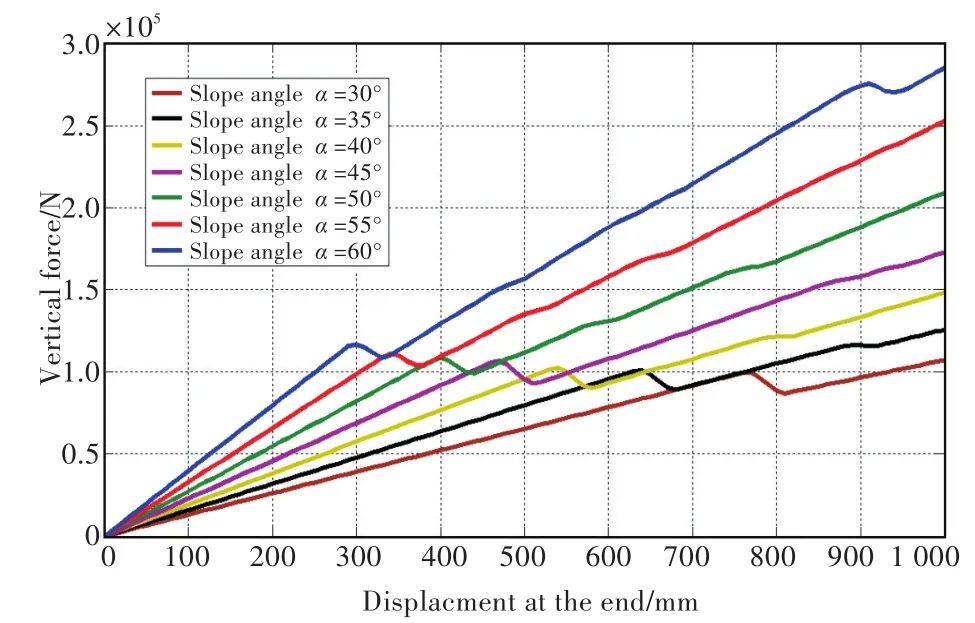
图15 斜坡结构受到的垂直冰力与水平位移之间的关系Fig.15 Relationship between vertical force and displacement of sloping structure

对于不同倾角的斜坡结构，随着斜坡结构倾角的增加，冰排出现初始失效时对应的斜坡结构受到的水平冰力也随之增加。斜坡结构倾角为30°时对应的冰排失效时结构受到的水平冰力为5.75×104N，而随着斜坡结构倾角的增加，当斜坡结构倾角为60°时对应的水平冰力达到2.02×105N，比倾角为30°时对应的水平冰力增加了351%。但冰排出现初始失效时对应的斜坡结构受到的垂直冰力基本不随斜坡结构倾角的变化而变化。斜坡结构倾角为30°时对应的冰排失效时结构受到的垂直冰力为9.96×104N，而随着斜坡结构倾角的增加，当斜坡结构倾角为60°时对应的垂直冰力为1.16×105N，相对倾角为30°时对应的垂直冰力没有明显的变化，只略微增加了16%。这主要是由于冰排在与斜坡结构作用时因为冰排发生弯曲变形而出现了弯折失效。而冰排的弯折失效主要由冰排受到的垂向分力引起，因为不同算例中冰排的几何尺寸和材料属性并未改变，所以其发生弯折失效所对应冰排受到的垂向分力基本保持不变。但随着斜坡角度的增加，冰排受到的水平分力随之增加，所以导致冰排出现初始失效时对应的斜坡结构受到的水平冰力随斜坡结构倾角的增加而增加，而垂直冰力基本不随斜坡结构倾角的变化而变化。

为了验证采用新型单元获得的计算结果，将采用直接分析法获得的冰排出现初始失效时的斜坡结构受到的水平和垂直冰力与采用Croasdale［14］提出的理论公式获得的解析解进行了对比，如图16和图17所示。从图16中的结果对比可以看出，通过新型单元获得的冰排出现初始失效时斜坡结构受到的水平和垂直冰力与解析解吻合良好。但随着斜坡结构倾角的增加，直接计算法相对于Croasdale［14］的理论公式结果之间的误差有逐渐增加的趋势，在结构倾角为60°时，最大误差为15%。引起误差的原因主要为冰排与斜坡结构作用时，在Croasdale［14］的理论公式中只考虑了冰排的弯曲，而忽略了斜坡结构对冰排沿水平方向存在的面内力，而在采用新型单元进行数值模拟时，斜坡结构存在对冰排的面内力，从而导致采用新型单元得到的冰力与Croasdale［14］的理论公式给出的冰力存在一定的误差。

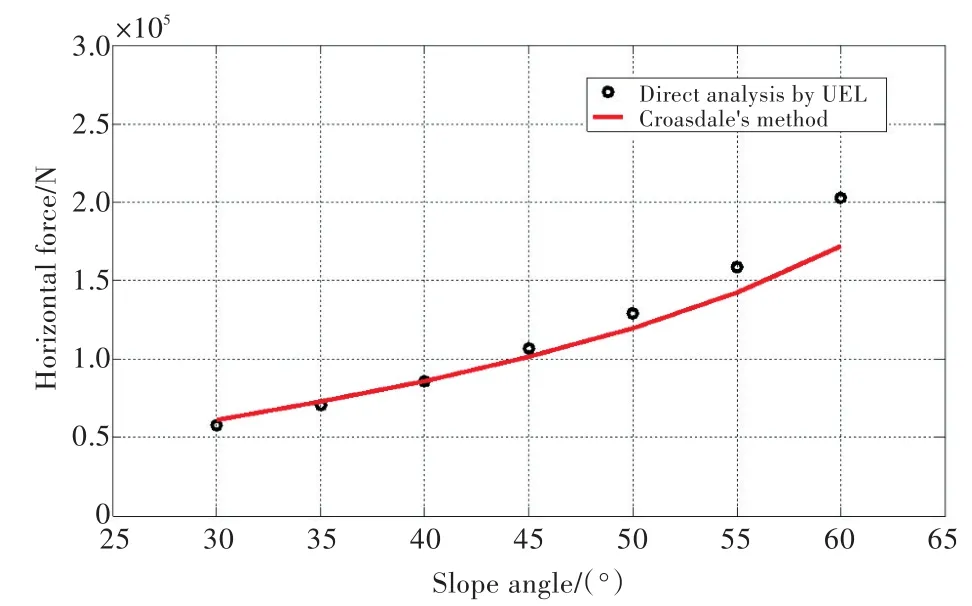
图16 直接计算法与Croasdale［14］公式水平方向冰力结果对比Fig.16 Comparison of horizontal force between direct analysis method and the equation presented by Croasdale［14］

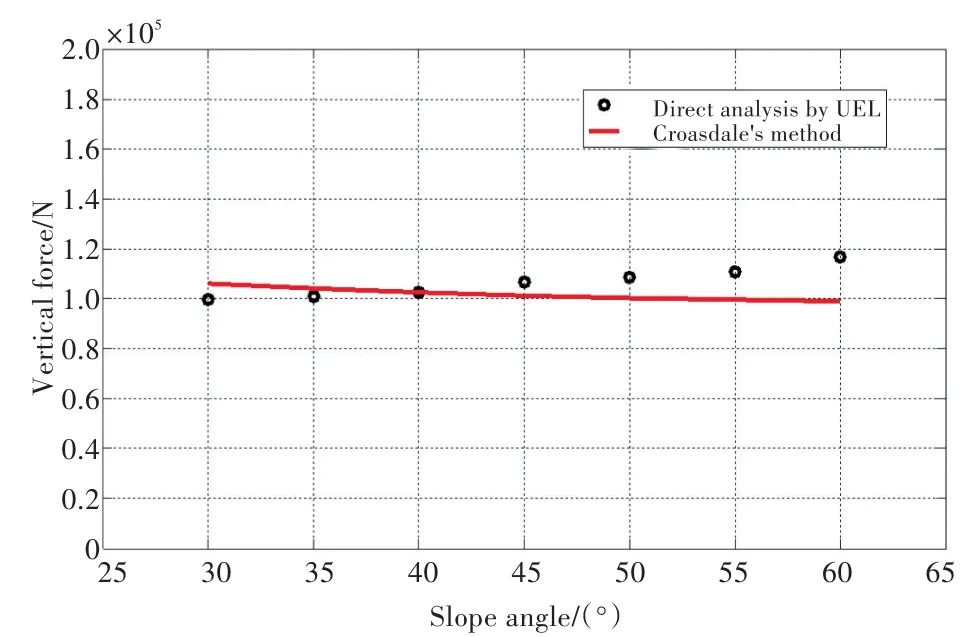
图17 直接计算法与Croasdale［14］公式垂向冰力结果对比Fig.17 Comparison of vertical force between direct analysis method and the equation presented by Croasdale［14］

2.4 冰排与圆锥结构的相互作用

计算圆锥结构与冰排作用时受到的冰力，并将所得计算结果与Ralston［3］给出的塑性极限分析解进行了比较，模型示意图如图18所示。计算圆锥结构的角度为30°～60°，间隔5°，圆锥结构的水线面直径D=12 m，圆锥结构水线面以上部分高度ht=3 m，水线面以下部分高度hb=6 m；冰排的长度l=100 m，宽度w=50 m，厚度h=0.8 m。建立的有限元模型共有41 760个单元，其中厚度方向有5个单元。

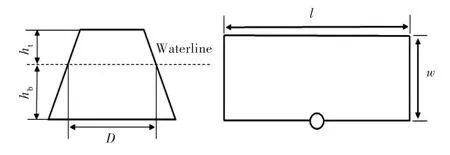
图18 圆锥结构示意图Fig.18 Schematic of cone structure

采用开发的新型单元模拟冰排与锥体结构的相互作用，得到的不同时刻下与锥角α=30°和60°的锥体结构作用时的冰排损伤分布图如图19和图20所示。其中蓝色部分表示未损伤单元，红色表示已出现损伤的单元。从图19和图20中可以看出，与锥角α=30°和60°的锥体结构作用时，冰排的损伤模式并未有明显的区别。冰排与锥体结构相互作用时，随着锥体结构水平位移的增加，冰排在上表面和下表面同时出现失效，并且随着锥体结构水平位移的增加，失效区域沿着径向发展，形成径向裂纹。当锥体结构的水平位移继续增加时，之前形成的径向裂纹沿着冰排的周向发展，形成周向裂纹，由于冰排的拉伸强度要明显小于冰排的压缩强度，所以冰排的下表面处先形成周向裂纹，且失效区域明显大于上表面，最终使得冰排的上表面和下表面处与锥体结构相邻的区域大面积失效。

图19 锥体结构锥角α=30°时冰排损伤分布Fig.19 Failure process of cone structure with cone angleα=30°

冰排与不同锥角的锥体结构作用时，锥体结构受到的水平和垂直冰力与锥体结构的水平位移之间的关系如图21和图22所示。从图21和图22中可以看出，随着锥体结构水平位移的逐渐增加，锥体结构受到的水平和垂直冰力也线性增加。当冰排中的应力状态达到单元失效准则所定义的失效面时，冰排出现失效。锥体结构受到的水平和垂直冰力随冰排水平位移的增加而下降。随着锥体结构水平位移的继续增加，冰排沿着锥体结构的斜面爬升，并且由于弹性基础的存在，导致锥体结构受到的冰力再次随锥体结构水平位移的增加而增加，使得锥体结构的受力再次继续上升。

图20 锥体结构锥角α=60°时冰排损伤分布Fig.20 Failure process of cone structure with cone angleα=60°

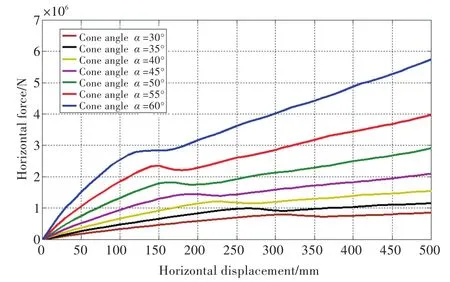
图21 锥体结构受到的水平冰力与水平位移之间的关系Fig.21 Relationship between horizontal force and displacement of cone structure

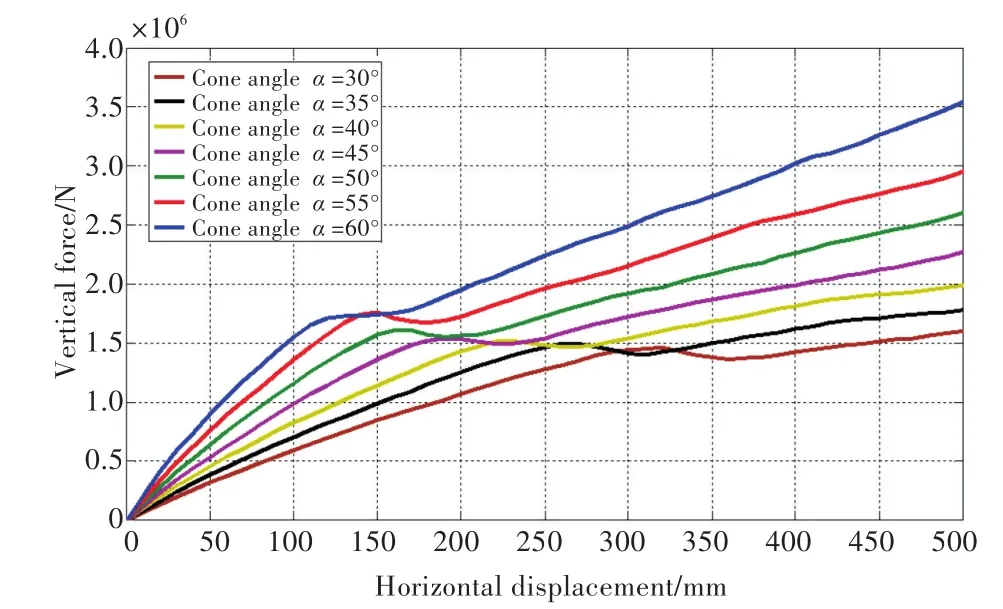
图22 锥体结构受到的垂直冰力与水平位移之间的关系Fig.22 Relationship between vertical force and displacement of cone structure

对于不同锥角的锥体结构，随着锥体结构锥角的增加，冰排出现初始失效时对应的锥体结构受到的水平冰力也随之增加。锥体结构锥角为30°时对应的冰排失效时结构受到的水平冰力为7.91×105N，而随着锥体结构倾角的增加，当锥体结构锥角为60°时对应的水平冰力达到了2.84×106N，比锥角为30°时对应的水平冰力增加了359%。但冰排出现初始失效时对应的锥体结构受到的垂直冰力基本不随斜坡结构倾角的变化而变化。锥体结构锥角为30°时对应的冰排失效时结构受到的垂直冰力为1.4×106N，而随着锥体结构倾角的增加，当锥体结构锥角为60°时对应的垂直冰力为1.74×106N，相对锥角为30°时对应的垂直冰力没有明显的变化，只略微增加了20%。但冰排出现初始失效时对应的锥体结构受到的垂直冰力基本不随锥体结构锥角的变化而变化。导致这一现象的原因与冰排和斜坡结构作用时类似，主要是由于冰排在与锥体结构作用时冰排因弯曲变形而出现弯折失效。而冰排的弯折失效由冰排受到的垂向分力引起，因为不同算例中，冰排的几何尺寸和材料属性并未改变，所以其发生弯折失效所对应的冰排受到的垂向分力也基本保持不变。但随着锥体结构锥角的增加，冰排受到的水平分力也随之增加，所以导致冰排出现初始失效时对应的锥体结构受到的水平冰力随锥体结构锥角的增加而增加，但垂直冰力基本不随锥体结构锥角的变化而变化。

为了验证采用新型单元获得的计算结果，将采用直接分析法获得的冰排出现初始失效时的锥体结构受到的水平和垂直冰力与采用Ralston［3］提出的理论公式获得的解析解进行了对比，如图23和图24所示。从图中的结果对比可以看出，通过新型单元获得的冰排出现初始失效时的锥体结构受到的水平冰力与解析解吻合良好，最大误差在14%左右。但通过新型单元获得的冰排出现初始失效时的锥体结构受到的垂直冰力与解析解的最大误差在30%左右。引起误差的原因主要有：

在所开发的新型单元中，冰被当作弹脆性材料来处理，而在Ralston［3］的理论公式中冰被当作理想弹塑性材料。由于弹塑性材料在达到屈服点后仍能承受一定的载荷，而弹脆性材料则不行，所以导致Ralston［3］给出的理论公式预测的冰力要比采用新型单元计算得到的冰力大。

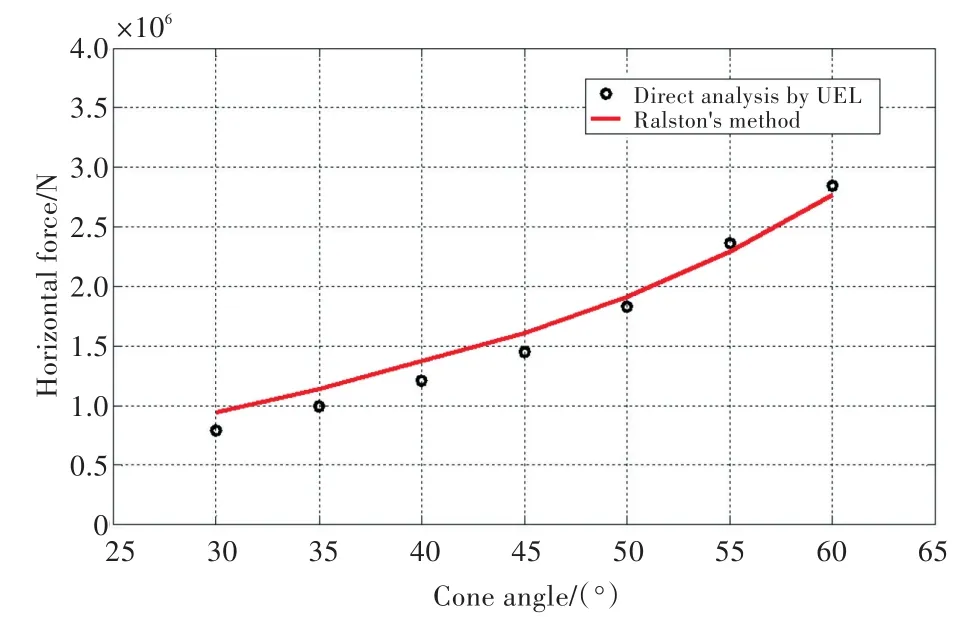
图23 直接计算法与Ralston［3］公式水平方向冰力结果对比Fig.23 Comparison of horizontal force between direct analysis method and the equation presented by Ralston［3］

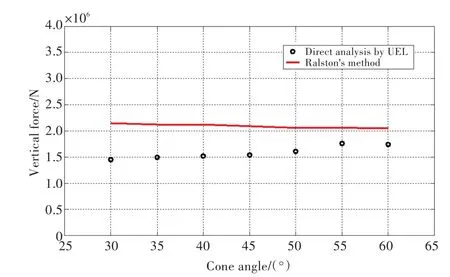
图24 直接计算法与Ralston［3］公式垂向冰力结果对比Fig.24 Comparison of vertical force between direct analysis method and the equation presented by Ralston［3］

在Ralston［3］的理论公式中，冰排与锥体结构之间的接触被理想化为完全接触，而在采用新型单元进行数值模拟时，从前述冰排与锥体结构相互作用时冰排的损伤分布图中可以看出，冰排与锥体结构并非完全接触。

冰排与锥体结构作用时，在Ralston［3］的理论公式中只考虑了冰排的弯曲，而忽略了锥体结构对冰排沿水平方向存在的面内力，而在采用新型单元进行数值模拟时，锥体结构存在对冰排的面内力，从而导致采用新型单元得到的冰力与Ralston［3］的理论公式给出的冰力存在一定的误差。

3 结 论

本文基于ABAQUS自定义单元子程序，结合Reinicke和Remer提出的各向同性海冰失效准则和弹性基础假定，开发了用于模拟海冰失效的8节点六面体单元。同时采用不同算例和相关理论公式对所开发的单元进行了验证，得出以下结论：

1）进行不同算例的计算后发现，使用直接计算法得到的结果与规范公式得到的结果吻合良好，说明了直接计算法的可行性；

2）在计算规范公式所没有的冰情和结构型式时直接计算法可以给出可信的结果，同时由于理论方法只能给出结构的最大受力，而直接计算法能够直观地给出冰损伤的过程及对应的结构受力变化过程，因而直接计算法可以为冰区结构设计提供一定的参考。

［1］BERCHA F G，DANYS J V.Prediction of ice forces on conical offshore structures［C］//Proceedings of the 3rd International Symposium on Ice Problems.Hanover，NH：Dartmouth College，1975：18-21.

［2］CROASDALE K R，CAMMAERT A B，METGE M.A method for the calculation of sheet ice loads on sloping structures［C］//Proceedings of the 12th IAHR Sympo⁃sium on Ice Problems.Trondheim，Norway：Norwe⁃gian Institute of Technology，1994.

［3］RALSTON T D.Plastic limit analysis of sheet ice loads on conical structures［M］//International Union of Theo⁃retical and Applied Mechanics Symposium on Physics and Mechanics of Ice.Berlin Heidelberg：Springer，1980：289-308.

［4］李锋，岳前进.冰在斜面结构上的纵横弯曲破坏分析［J］.水利学报，2000，31（9）：44-47.LI F，YUE Q J.Failure of ice sheet under simultane⁃ously longitudinal and transverse load on slope struc⁃tures［J］.Journal of Hydraulic Engineering，2000，31（9）：44-47（in Chinese）.

［5］Bureau Veritas.Ice characteristics and ice/structure in⁃teractions guidance note NI 565 DT R00 E［R］.［S.l.］：Bureau Veritas，2010.

［6］American Petroleum Institute.Recommended practice for planning，designing and constructing structures and pipelines for arctic conditions［S］.2nd ed.Wash⁃ington，DC：API Publications，1995.

［7］SAND B，HORRIGMOE G.Simulation of ice forces on sloping structures［C］//The Eighth International Off⁃shore and Polar Engineering Conference.Montreal，Canada：The International Society of Offshore and Po⁃lar Engineers，1998.

［8］DERRADJI-AOUAT A.Explicit FEA and constitutive modelling of damage and fracture in polycrystalline ice-simulations of ice loads on offshore structures［C］//18th International Conference on Port and Ocean Engi⁃neering under Arctic Conditions（POAC'05）.New York，United States：POAC，2005.

［9］黄焱，袁光奇，马健钧.海冰弯曲破坏下的破坏准则数值模拟方法研究［J］.数学的实践与认识，2014，44（23）：115-126.HUANG Y，YUAN G Q，MA J J.Methodology re⁃search on the numerical simulation of the bending fail⁃ure of sea ice［J］.Mathematics in Practice and Theory，2014，44（23）：115-126（in Chinese）.

［10］宋安，孙金亮，史庆增，等.作用在引航导堤堤头冰力的模型试验研究［J］.天津大学学报，2006，39（5）：537-542.SONG A，SUN J L，SHI Q Z，et al.Model test for ice force on the bank-head of the lead-navigating bank［J］.Journal of Tianjin University，2006，39（5）：537-542（in Chinese）.

［11］REINICKE K M，REMER R.A procedure for the de⁃termination of ice forces-Illustrated for polycrystal⁃line ice［C］//Proceedings of the 4th IAHR Symposium on Ice Problems.Luleå，Sweden：［s.n.］，1978.

［12］ZIENKIEWICZ O C，TAYLOR R L.有限元方法：第1卷：基本原理［M］.曾攀，译.5版.北京：清华大学出版社，2008.

［13］孔娟，张勇.弹性地基板单元在ABAQUS中的开发与 应 用［J］.燕 山 大 学 学 报 ，2010，34（4）：370-376.KONG J，ZHANG Y.Secondary development and ap⁃plication ofelastic foundation plate elementin ABAQUS［J］.Journal of Yanshan University，2010，34（4）：370-376（in Chinese）.

［14］CROASDALE K R.Forces on fixed rigid structures.Working group on ice forces on structures-a state-of-the-art-report［R］.Hanover，New Hamp⁃shire：CRREL，1980.

Development of sea ice element and direct analysis method of predicting ice loads based on ABAQUS

GONG Yufeng1，ZHANG Zhengyi1，2，3，LIU Jingxi1，2，3，DONG Wen1，XIE De1，2，3
1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China
2 Hubei Key Laboratory of Naval Architecture&Ocean Engineering Hydrodynamics，Wuhan 430074，China
3 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China

With the global temperature continuing to rise,the Arctic ice is melting.The development of the Arctic route and exploitation of Arctic resources are drawing the wide attention of international society.Many countries are starting a new round of the construction of polar ships.In recent years,domestic and foreign researchers have begun to focus on the numerical study of ice loads on structure.However,the current commercial finite element software lacks a specialized element used for simulating the mechanical properties of sea ice.This lack increases the difficulty of the numerical study of ice loads on structure.In this paper,based on Reinicke and Remer's elliptic failure criteria and Winkler's elastic foundation,an element has been developed to simulate the bending failure of isotropic granular ice.The ice loads of typical marine structures,such as slope structure and conical structure,are calculated through the direct analysis method with the developed element.A comparison between the results of the direct analysis method and analytical method show good agreement.In brief,the proposed direct analysis method may provide tools and certain references for structural design in an ice environment.

ice load；direct analysis method；ABAQUS；hourglass control；user-defined element

U661.4

：ADOI：10.3969/j.issn.1673-3185.2017.03.011

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1251.020.html期刊网址：www.ship-research.com

龚榆峰，张正艺，刘敬喜，等.基于ABAQUS的海冰单元开发及冰载荷直接计算法［J］.中国舰船研究，2017，12（3）：75-85.

GONG Y F，ZHANG Z Y，LIU J X，et al.Development of sea ice element and direct analysis method of predicting ice loads based on ABAQUS［J］.Chinese Journal of Ship Research，2017，12（3）：75-85.

2016-10-12< class="emphasis_bold">网络出版时间

时间：2017-5-12 12:51

国家自然科学基金资助项目（51579110）；国家高技术研究发展计划资助项目（2012AA112601）；华中科技大学自主创新研究基金资助项目（2015TS004）

龚榆峰，男，1988年生，博士生。研究方向：船体结构。E-mail：D201277373@hust.edu.cn

刘敬喜（通信作者），男，1975年生，博士，副教授。研究方向：船体结构。E-mail：Liu_Jing_Xi@hust.edu.cn