水下非接触爆炸下船体爆炸弯矩简化计算方法

吴广明，陈炜，吴敌，李正国

中国舰船研究设计中心，上海201108

水下非接触爆炸下船体爆炸弯矩简化计算方法

吴广明，陈炜，吴敌，李正国

中国舰船研究设计中心，上海201108

［目的］水下非接触爆炸冲击能引起船体强烈的总纵弯曲运动，威胁船体总纵强度。采用详细的有限元建模进行水下非接触爆炸计算虽然可以获得船体爆炸弯矩，进而计算船体水下非接触爆炸作用下的船体总纵强度，但该方法工作量较大且较为复杂。为此，［方法］提出一种基于梁模型的船体水下非接触爆炸弯矩简化计算方法，运用ABAQUS有限元软件，建立船体详细有限元模型和船体梁简化模型，并分别进行水下非接触爆炸工况下危险剖面的爆炸弯矩计算。［结果］计算结果表明，建立的船体梁简化模型不仅建模简单，而且爆炸弯矩计算精度良好。［结论］所得结果可为水下非接触爆炸下船体爆炸弯矩的快速估算提供参考。

船体梁；水下非接触爆炸；总纵强度；爆炸弯矩

0 引 言

舰船抗水下非接触爆炸冲击的能力历来受到世界各海军强国的重视。水下非接触爆炸产生的冲击波载荷不但会引起船体结构的局部破坏，而且冲击波过后由于气泡脉动载荷持续时间长，能量占整个水下爆炸的一半左右，还将诱发船体梁强烈的鞭状运动，严重威胁船体总纵强度。特别是当船体梁低阶频率与气泡脉动频率相近时，剧烈的鞭状运动能使船体壳板撕裂、屈曲甚至是折断，造成灾难性的后果［1-2］。可见，对水下非接触爆炸冲击下船体总纵强度的研究具有重要的军事价值。

所谓爆炸弯矩，是指在水下爆炸作用下，船体梁在爆炸冲击激励力、重力、浮力和惯性力等的联合作用下产生的动态力矩。目前，针对水下爆炸下的舰船总强度及爆炸弯矩已有一些研究。朱锡等［3］采用静置气泡假设，建立了水下爆炸气泡作用后船体总纵弯曲的理论计算方法并进行了强度校核。岳永威［4］对考虑由水下爆炸气泡引起的爆炸弯矩的运输船总强度计算衡准进行了研究。张弩［5］基于势流理论建立了水下爆炸船体梁爆炸弯矩理论计算方法。李烨等［6］使用ABAQUS软件对某船典型剖面在水下爆炸下的动弯矩进行分析，并结合各总强度规范提出了校核衡准数定义。崔杰等［7］基于Taylor平板理论，在修正船体耦合压力的基础上，理论推导建立了水下爆炸下船体梁爆炸冲击弯矩计算模型。

由以上研究可知，使用爆炸弯矩载荷能进行水下爆炸下舰船总强度的计算校核。由于使用详细有限元建模方法和理论方法计算爆炸弯矩较为繁琐，故本文将拟出一种基于梁模型的船体水下非接触爆炸弯矩简化计算方法，并运用ABAQUS有限元软件从详细有限元模型和船体梁简化模型这2个方面进行水下非接触爆炸工况下的危险剖面爆炸弯矩计算。通过对这2种计算方法的研究，为水下非接触爆炸下船体剖面爆炸弯矩提供一种新的快速估算方法。

1 简化计算方法描述

水下非接触爆炸下船体爆炸弯矩简化计算方法是在ABAQUS详细有限元法的基础上，在简化建模的条件下提出的一种计算方法，其主要思路是用船体梁模型代替全船详细有限元模型。

简化计算模型包括船体结构模型和水域模型。船体结构模型分为2个部分：船体梁和船体外壳。实际船体结构到船体梁的简化过程参照经典船体梁理论进行，其与运用20站船体梁剖面要素及20站重量等进行总振动计算的简化过程一致；各站船体外壳与实船完全相同，在软件中通过将模型建成分离的刚性外壳来定义每站外壳与对应船体梁节点的刚性相连。水域模型与详细有限元计算模型一致。爆炸载荷、水域和船体外壳的耦合方式以及水下非接触爆炸的计算过程与详细有限元法也一致。由于外壳与船体梁节点刚性相连，爆炸载荷会通过耦合约束传递到船体梁结构，引发船体梁弯曲运动，从而实现水下非接触爆炸下船体梁总纵弯曲运动的模拟。

2 计算研究

2.1 工况载荷

由位于船舯的水下爆炸所引起的总纵弯曲相对艏艉的爆炸更加剧烈。本文将爆心设置于船舯，选取板壳冲击因子的工况（W为TNT当量，kg；R为爆心与结构的最短距离，m），爆炸攻角θ分别为90°和30°，如图1所示。该工况为舰船非接触爆炸总纵强度计算考核的常用工况。

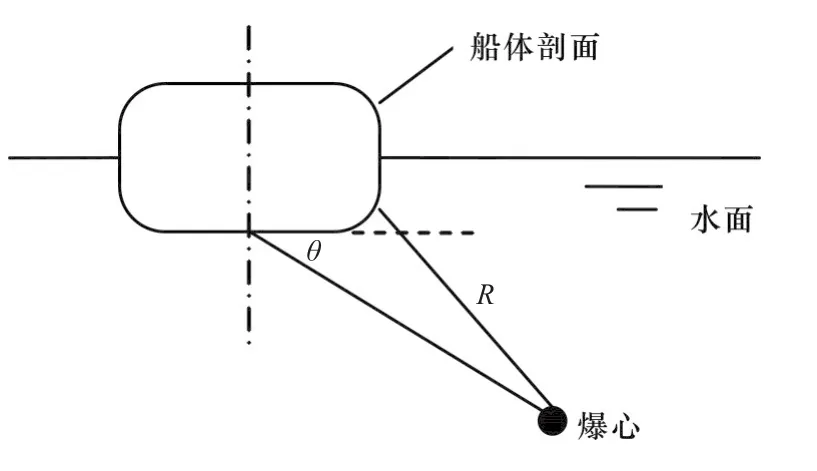
图1 计算工况示意图Fig.1 Schematic diagram of load case

气泡脉动对舰船总纵弯曲的影响至关重要，因此必须考虑气泡脉动载荷。本文采用ABAQUS软件内置的Geers-Hunter气泡模型。该模型包括水下爆炸冲击波阶段和气泡脉动阶段，能较好地反应水下非接触爆炸载荷的特点［8-9］。当t＜7Tc（t为时间，Tc为爆炸压力特征时间）时，为冲击波阶段，采用双指数衰减形式进行冲击波压力拟合：

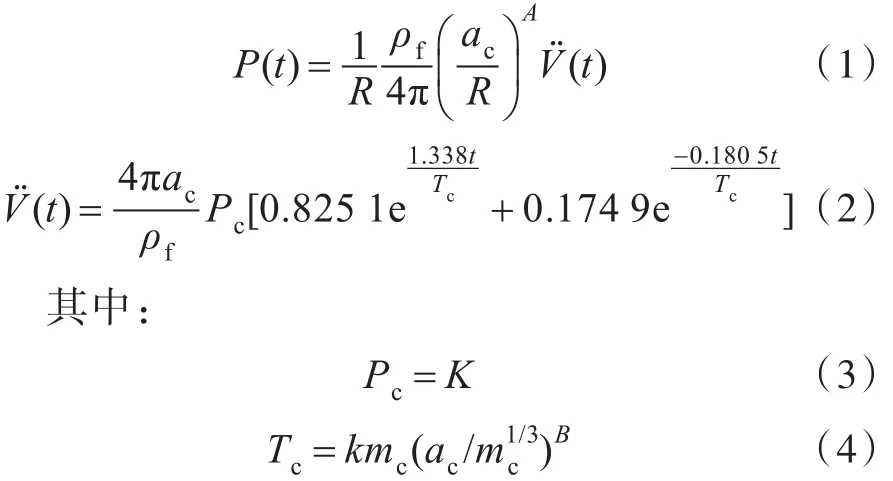
当t≥7Tc时，为气泡脉动阶段，采用双渐进法推导得出：

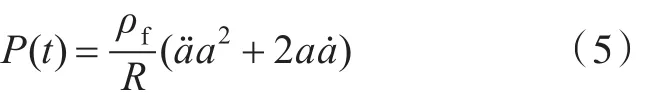
以上式中：P(t)为冲击波压力；ρf为流体密度；Pc，Tc分别为爆炸特征压力和特征时间；mc，ac分别为药包初始质量和初始半径；K，k，A，B为材料常数；a为气泡半径，通过微分方程组求得［8-9］。

船体梁的鞭状运动包括中拱中垂往复的过程，持续时间较长，船体运动以及水面反射波容易引起水中空化效应。而ABAQUS软件水下爆炸模块的总波公式（Total wave formulation）计算方法则能模拟水域的空化效应，故本文采用总波公式进行计算。

2.2 详细有限元建模

使用MSC.Patran建立详细有限元数值模型，如图2所示，然后导入ABAQUS中赋予属性并定义水下非接触爆炸下的计算参数。在船体结构有限元模型中，对船体主要结构，包括甲板大开口等进行详细建模，并使用质量点模拟设备等的重量，以使全船重量分布与实船一致。使用壳单元模拟各层甲板、外板和主隔壁等板材，使用梁单元模拟纵骨、T型材和支柱等。模型共包含S3R单元2 095个，S4R单元166 367个，梁单元120 574个，单元尺寸为0.25～0.4 m。船体材料为高强度钢，材料密度ρ=7 850 kg/m3，弹性模量E=210 GPa，泊松比为0.3。为考虑爆炸冲击中的应变率强化效应，采用分段形式定义材料弹塑性特征。程序将根据计算中的实时应变率插值计算各时刻船体材料的动态屈服应力。

在舰船受水下爆炸冲击的有限元计算中，船体外的水域不仅起到传播爆炸冲击波、与结构耦合传递载荷的作用，还对船体动态响应具有重要影响。本文在爆炸冲击计算中建立的水域模型能够模拟附连水质量的影响，而不用在船体模型上额外施加附加附连水质量。考虑到计算成本与精度的平衡，建立了4倍于结构大小的水域模型［10］，其中包括520 657个声学AC3D4R单元。流场网格划分采用渐变方法，网格尺寸从船体湿表面到外围水域逐渐加大。在与船体湿表面耦合的区域，采用与船体单元尺寸相似的网格大小，以保证足够的计算精度；在离船体较远的外围水域，加大网格尺寸以提高计算效率。将水域底部设置为无反射边界条件，水面设置为零压力边界条件，并与船体外板表面使用Tie方法建立耦合。最终，得到全船详细有限元及流场耦合模型（图2）。

图2 详细有限元及流场耦合模型Fig.2 Finite element model and fluid-coupled model of ship

2.3 基于梁模型的简化建模

建立全船详细有限元模型并进行水下非接触爆炸冲击计算能够得到校核剖面的爆炸弯矩载荷，但只有船体构件和尺寸均确定时才能建立准确的全船详细有限元模型，且建立全船模型费时费力，计算平台要求较高。可运用有限元软件建立船体梁简化计算模型，该模型包括船体结构和水域模型2个部分。其中船体结构模型又分为2个部分：船体梁和船体外壳。船体梁模型如图3所示。将船体梁分为20站进行模拟，大致位于中和轴的位置采用梁单元（B31），每站通过赋予站内质量、惯性矩、剪切面积等参数来近似替代实际船体结构。站内质量按实际全船质量分布得到，惯性矩和剪切面积则通过各站实际船的剖面要素计算得到。具体简化过程参照经典的船体梁理论进行，与运用20站船体梁剖面要素及20站重量进行总振动计算的简化过程一致。各站的船体外壳与实船完全相同，在软件中设置为分离的刚性体，而不定义各外壳的接触关系，因而在计算中各外壳不会发生接触及碰撞效应，互不干扰。船体外壳的网格尺寸与详细模型外板的网格大小相近，各站外壳所有的节点通过Coupling运动耦合方式与对应站的船体梁节点刚性连接，如图4所示（为表示船体梁结构，图中梁单元已放大）。水域大小、网格划分及边界条件则均与详细有限元模型水域相同。

图3 船体梁简化模型及流场耦合模型Fig.3 Simplified hull girder model and fluid-coupled model

图4 船体结构模型耦合示意图Fig.4 Schematic diagram of hull girder coupling

2.4 总振动固有频率计算验证

水下非接触爆炸下，船体梁的垂向低阶频率对总纵弯曲有明显的影响。对全船详细有限元模型和船体梁简化模型进行总振动固有频率计算：总强度计算模型不包括水域模型，按照刘易斯附连水计算方法，根据各站形状和三维流动系数做修正，从而得到各站附连水质量［11］。对于详细模型，将附连水质量均分到各站吃水以下船体外板的有限元节点上；对于简化模型，将各站附连水质量作为质量点施加到相应的梁节点上。计算结果表明，2种模型各阶振型良好。船体梁简化模型与详细有限元模型的垂向一阶、二阶频率误差均较小，船体梁垂向前两阶振型图如图5所示。通过总振动固有频率计算，表明本文2种模型的刚度与重量分布均相似，可进行水下非接触爆炸计算研究。

图5 船体梁垂向前两阶振型Fig.5 First and second order vibration mode of hull girder

2.5 计算结果分析

进行总纵强度计算研究时，需要选择总强度研究剖面。在水下非接触爆炸下，船体梁的总纵弯曲运动主要频率成分为垂向前三阶频率［4］。对垂向挠曲振动主振型进行分析，发现只考虑一阶振型时，L/2（L为船长）船舯剖面弯矩最大，只考虑二阶振型时，沿船长L/4和3L/4附近剖面的弯矩最大。由振型线性叠加原理可知，在综合考虑前三阶振型的情况下，叠加后的最大爆炸弯矩的可能位置有3个：L/4，L/2和3L/4处。本文的总纵强度研究选取以上3个位置附近剖面模数较小的危险剖面。

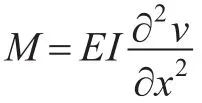
分别使用详细有限元模型和船体梁简化模型计算本文水下非接触爆炸工况下各危险剖面的爆炸弯矩。由于爆炸冲击下的鞭状运动以垂向前三阶频率为主，故以船体梁第3阶垂向频率为截止，对原始爆炸弯矩曲线进行低通滤波，得到滤波后的曲线作为最终爆炸弯矩的计算结果［12］。

2.5.1 工况1

工况1时，爆炸攻角θ=90°，爆心位于船舯正下方位置。3个危险剖面的爆炸弯矩时历曲线对比如图6所示。表1所示为该工况下的中拱中垂最大爆炸弯矩。

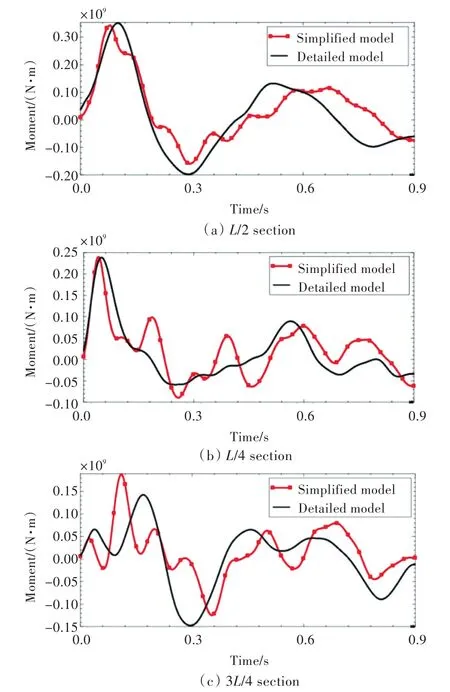
图6 工况1时的爆炸弯矩曲线对比Fig.6 Comparison of explosion bending moment curves for case 1

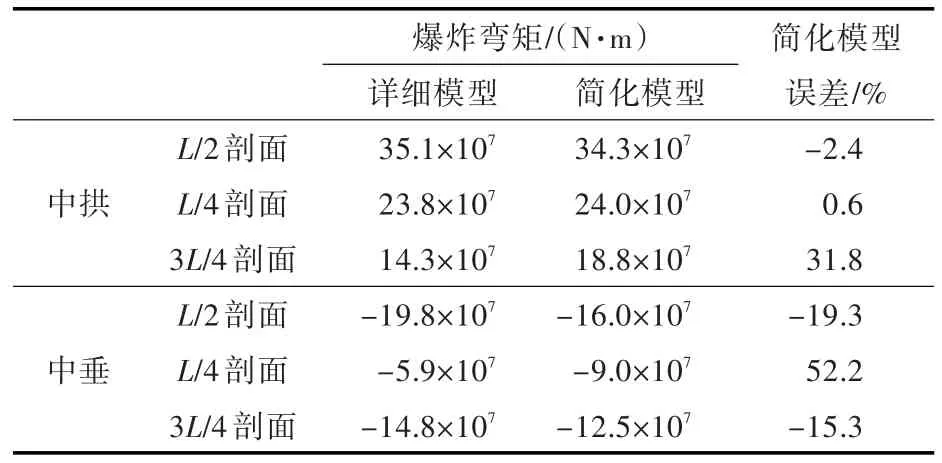
表1 工况1时各剖面最大爆炸弯矩Table 1 Maximum explosion bending moment of sections in case 1

由图6可以看到，在该工况下，详细有限元模型和船体梁简化模型的爆炸弯矩曲线在第1个波峰时间段重和度很高，而后稍有差异，但变化趋势相同，都有明显的中拱中垂现象。由于船舯的总纵运动主要为垂向一阶成分，而简化模型的一阶频率与详细模型相近，故在L/2剖面2个模型的弯矩曲线精度都很高。L/4剖面和3L/4剖面的垂向二、三阶频率成分相对较高，简化模型与详细模型因前三阶频率不同造成2条曲线在相位上略有差异。

通过比较中拱中垂的爆炸弯矩数值（表1）发现：危险剖面的中拱爆炸弯矩范围为14×107～35×107N·m，中垂的爆炸弯矩范围为 5×107～20×107N·m；2种模型下L/2剖面处的弯矩和其他剖面处的相比要大。简化模型在L/2剖面处精度较好，中拱中垂弯矩误差分别为-2.4%和-19.3%；其他剖面处计算精度各有不同，平均误差约为30%。

2.5.2 工况2

工况2时，爆炸攻角θ=30°，爆心位于船舯右舷位置。3个危险剖面的爆炸弯矩时历曲线对比如图7所示。表2所示为该工况下的中拱中垂最大爆炸弯矩。

图7 工况2时爆炸弯矩曲线对比Fig.7 Comparison of explosion bending moment curves for case 2

表2 工况2时各剖面最大爆炸弯矩Table 2 Maximum explosion bending moment of sections in case 2

由图7可知，与工况1类似，从船体受到冲击波的作用到第1次中拱时，各曲线基本吻合，特别是L/2船舯剖面处的弯矩曲线几乎重合。而后简化模型曲线的变化趋势与详细有限元模型的相同，中垂中拱的时间略有错位。产生此现象的原因：一方面，是2个模型在垂向前三阶的频率不同；另一方面，是工况2为爆炸冲击呈30°入射，能引起船体梁一定的水平运动，两模型水平特征的差异有可能会引起爆炸弯矩曲线的不同。

比较工况2下的爆炸弯矩数值（表2）发现：危险剖面中拱爆炸弯矩的范围为7×107～26×107N·m，中垂爆炸弯矩的范围为6×107～15×107N·m，整体上比工况1略小；简化模型在L/2剖面处的中拱中垂计算误差分别为9.9%和-28.2%，其他剖面处的计算精度各有不同，平均误差约为30%。

2.5.3 结果探讨

本文的船体梁简化模型和详细有限元模型相比在建模上花费的时间少，计算效率高，得到的爆炸弯矩曲线与详细有限元模型较为一致，中拱中垂爆炸弯矩的平均计算精度良好，对水下非接触冲击下，舰船爆炸弯矩的快速估算具有一定的参考作用。需要注意的是：当水下爆炸冲击因子较大时，实船可能会发生较大的塑性变形，而简化模型因只有梁结构，故并不能模拟实船内部复杂的塑性变形情况，会产生较大的计算误差。所以，本文的船体梁简化模型对爆炸弯矩的计算适用于冲击因子较小或实船塑性应变较小的情况。

3 结 论

本文提出了一种水下非接触爆炸下船体爆炸弯矩的简化计算方法。运用ABAQUS软件，分别建立详细有限元模型和基于船体梁的简化模型，并分别对水下爆炸冲击下舰船所受到的爆炸弯矩进行计算对比，得到结论如下：

1）在本文的冲击因子下，危险剖面的爆炸弯矩为同一量级。其中，船舯L/2剖面处的爆炸弯矩值最大。攻角θ=90°时各剖面的爆炸弯矩比θ=30°时的大。

2）通过本文提出的水下非接触爆炸下船体爆炸弯矩简化计算方法，可快捷建立船体结构模型，模拟水下非接触爆炸作用下的船体总纵弯曲运动，计算获得爆炸弯矩曲线。其中，船舯L/2剖面处的最大中拱爆炸弯矩误差小于10%，其他剖面处的中垂中拱爆炸弯矩误差约为30%。所得结果可为舰船水下非接触爆炸冲击下的爆炸弯矩快速估算提供参考。

3）本文仅对典型工况下采用20站梁的爆炸弯矩的简化计算方法进行了研究，对工程中最常遇到工况下的船体爆炸弯矩的简化计算具有一定的实用参考价值。而有关更多工况下该方法的计算准确性，以及更少或更多站时该简化方法的计算收敛性，还有待在今后的工作中进一步开展计算研究。

［1］姚熊亮，张阿漫，许维军，等.基于ABAQUS软件的舰船水下爆炸研究［J］.哈尔滨工程大学学报，2006，27（1）：37-41.YAO X L，ZHANG A M，XU W J，et al.Research on warship underwater explosion with ABAQUS software［J］.Journal of Harbin Engineering University，2006，27（1）：37-41（in Chinese）.

［2］张弩，于馨.水下爆炸冲击波与气泡载荷作用下船体结构的动响应［J］.中国舰船研究，2014，9（1）：99-104.ZHANG N，YU X.Dynamic response of a hull struc⁃ture subjected to underwater explosion shock wave and bubbles［J］.Chinese Journal of Ship Research，2014，9（1）：99-104（in Chinese）.

［3］朱锡，方斌.舰船静置爆炸气泡时总纵强度计算方法研究［J］.海军工程大学学报，2007，19（6）：6-11.ZHU X，FANG B.Study on longitudinal strength calcu⁃lation method of hull standing above an explosion bub⁃ble［J］.Journal of Naval University of Engineering，2007，19（6）：6-11（in Chinese）.

［4］岳永威.大型运输船水下爆炸结构强度计算方法研究［D］.哈尔滨：哈尔滨工程大学，2013.YUE Y W.Research on structural strength calculation method of large-scale transport ship subjected to un⁃derwater explosion［D］.Harbin：Harbin Engineering University，2013（in Chinese）.

［5］张弩.水下爆炸气泡作用下船体总纵强度估算方法［J］.中国舰船研究，2014，9（6）：14-18，25.ZHANG N.The evaluation method of the longitudinal strength of a ship hull subjected to the bubble load in underwater explosion［J］.Chinese Journal of Ship Re⁃search，2014，9（6）：14-18，25（in Chinese）.

［6］李烨，王雷，陈莹玉，等.水下爆炸作用下计及冲击动弯矩的舰船总强度分析［J］.舰船科学技术，2015，37（8）：12-17.LI Y，WANG L，CHEN Y Y，et al.Analysis of global strength of hull subjected to non-contact explosive load considering the impact bending moment［J］.Ship Science and Technology，2015，37（8）：12-17（in Chi⁃nese）.

［7］崔杰，李佳，陈莹玉，等.水下爆炸冲击波作用下舰船总纵强度工程预报方法［J］.噪声与振动控制，2015，35（6）：110-114，180.CUI J，LI J，CHEN Y Y，et al.Engineering forecast method for the longitudinal strength of ship hulls sub⁃jected to underwater explosion shock wave［J］.Noise and Vibration Control，2015，35（6）：110-114，180（in Chinese）.

［8］GEERS T L，HUNTER K S.An integrated wave-ef⁃fects model for an underwater explosion bubble［J］.The Journal of the Acoustical Society of America，2002，111（4）：1584-1601.

［9］GEERS T L，PARK C K.Optimization of the G&H bubble model［J］.Shock and Vibration，2005，12（1）：3-8.

［10］BLEVINS R D.Formulas for natural frequencies and mode shapes［M］.［S.l.］：Fruger Publishing Co.，1979.

［11］金咸定，夏利娟.船体振动学［M］.上海：上海交通大学出版社，2011.

［12］张阿漫，郭君，孙龙泉.舰船结构毁伤与生命力基础［M］.北京：国防工业出版社，2012.

Calculation of explosion bending moment in hull girders subjected to non-contact underwater explosions

WU Guangming，CHEN Wei，WU Di，LI Zhengguo
Shanghai Division，China Ship Development and Design Center，Shanghai 201108，China

Non-contact underwater explosion can generate violent movement on hull girders，which may cause longitudinal strength problems.The explosion bending moment can be calculated using a detailed finite element ship model，but this costs considerable working time.This paper advances a new method for calculating explosion bending moment by a hull girder model.The explosion bending moment of typical ship sections is calculated according to a detailed ship model and simplified hull girder model using ABAQUS software.Comparisons between the results indicate that the simplified hull girder model is easily created and has good precision，enabling it to provide a reference for the estimation of explosion bending moment in hull girders subjected to non-contact underwater explosion.

hull girder；non-contact underwater explosion；longitudinal strength；explosion bending moment

U661.43

：ADOI：10.3969/j.issn.1673-3185.2017.03.009

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1253.024.html期刊网址：www.ship-research.com

吴广明，陈炜，吴敌，等.水下非接触爆炸下船体爆炸弯矩简化计算方法［J］.中国舰船研究，2017，12（3）：58-63.

WU G M，CHEN W，WU D，et al.Calculation of explosion bending moment in hull girders subjected to non-contact underwater explosions［J］.Chinese Journal of Ship Research，2017，12（3）：58-63.

2016-09-21< class="emphasis_bold">网络出版时间

时间：2017-5-12 12:53

中国舰船研究设计中心研发基金资助项目

吴广明（通信作者），男，1976年生，博士，高级工程师。研究方向：船体结构设计。E-mail：1078801933@qq.com

陈炜，男，1971年生，高级工程师。研究方向：船体结构设计