页岩气藏体积压裂水平井产能有限元数值模拟

何易东，任岚，赵金洲，李志强，邓鹏

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.中国石油塔里木油田分公司塔中油气开发部，新疆 库尔勒 841000）

页岩气藏体积压裂水平井产能有限元数值模拟

何易东1，任岚1，赵金洲1，李志强1，邓鹏2

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.中国石油塔里木油田分公司塔中油气开发部，新疆 库尔勒 841000）

考虑到压裂过程中的多重复合作用，将压后页岩储层分为支撑主裂缝、缝网波及区与未压裂区。考虑基岩纳米孔隙中气体吸附与解吸、Knudsen扩散、滑脱流、黏性流，以及水压诱导裂缝应力敏感效应，建立了页岩气藏体积压裂生产动态模拟的物理模型和渗流数学模型。结合Galerkin有限元方法，对基质和裂缝渗流方程进行空间上的离散，推导了三角形单元有限元数值模型，给出了压裂水平井二维渗流场内、外边界条件和水力裂缝处理方法，对时间域采用向后差分，最后顺序求解裂缝和基质压力方程，模拟了页岩气藏体积压裂水平井生产动态和压力场分布。该研究为页岩气储层体积压裂产能评价提供了理论模型，对于有限元法模拟双重介质渗流场和产能预测具有现实意义。

页岩气；体积压裂；双重介质；有限元；产能模拟

0 引言

近年来，页岩气藏的开发方兴未艾，然而页岩储层物性较差，基岩渗透率一般在10-9μm2数量级，孔隙度一般在4%～6%。同时，储层非均质性也较为严重，天然裂缝发育。通过水力压裂沟通储层天然裂缝，形成较大范围的网络裂缝，是实现该类储层有效开发的关键技术之一，油藏增产体积是衡量页岩气藏改造效果的关键参数［1］。页岩气的储集、运移机理和常规天然气存在较大差异，目前认为，页岩气主要以游离气和吸附气形式储集于基质纳米孔隙中，一部分以游离气形式储集于天然裂缝系统中，还有一部分是以溶解气形式储集于有机质干酪根中［2］。页岩储层中发育大量连通的纳米孔隙、不连通或闭合的天然微裂缝以及水力压裂形成的体积裂缝。页岩气在开采过程中将在纳米孔隙—微裂缝—水压体积裂缝多尺度空间进行流动传输。首先从纳米孔隙介质向微裂缝发生微观分子级的扩散流动汇聚，然后从微裂缝向宏观水力压裂体积裂缝发生宏观渗流［3］。页岩气开发过程中，流体传输机理和流动路径复杂，流态形式多样［4］，但目前对页岩气在储层中渗流机理认识还不清，页岩气储层体积压裂产能模拟方法也存在严重滞后。

应用有限元法可以较好地处理内外边界条件，且其网格划分的灵活性优于有限差分法。目前有限元法已经成功应用于模拟油气藏单相和多相流体流动［5-10］，但是对于模拟页岩这种双重介质气藏的研究较少［11］，特别是如何采用Galerkin有限元法模拟页岩气在多尺度空间中的复杂流动，建立相应的有限元数值求解模型，以及页岩储层压裂水平井考虑储层中流体为二维流动的内外边界条件处理方法尤为少见。

1 物理模型

对于天然裂缝发育、低水平主应力差的页岩储层，由于低黏度压裂液的携砂能力差，在压裂施工过程中形成一条高导流能力的支撑主裂缝，主裂缝之间出现相互连通的诱导裂缝网络［12］，从而形成一个体积压裂区。如图1所示，该复合气藏模型由支撑主裂缝、体积压裂区和未压裂区构成［13］。为便于工程上的模拟应用，该复合模型可以用离散裂缝描述支撑主裂缝，而采用双重介质模型来描述体积压裂区和未压裂区［14］，也可以将未压裂区考虑为单孔隙介质系统。

2 页岩气渗流数学模型

2.1 连续性方程

随着基质纳米孔隙半径的减小，气体分子平均自由程和流动空间的特征长度将越来越接近，此时，气体分子和孔壁的碰撞将会更加频繁，气体分子更容易表现出微观级的分子流态，这种效应使得储层表观渗透率进一步增加［15］。考虑纳米孔隙中气体滑脱、Knudsen扩散和黏性流的表观渗透率模型为

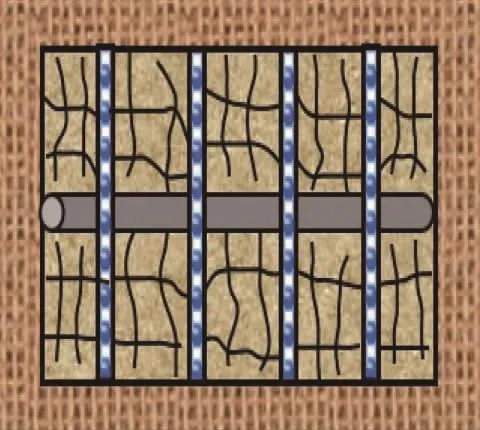
图1 页岩储层体积压裂产能模拟物理模型

页岩储层水力压裂后，气体将在由基质纳米孔隙、天然裂缝和人工裂缝组成的多尺度空间中运移，其流动机理复杂，主要包括基质中的吸附、解吸、Knudsen扩散、黏性流，以及裂缝中的黏性流［16-17］。由此，页岩基质系统中气体连续性方程为

页岩气在基质纳米孔隙中的吸附量可由Langmuir等温吸附方程描述：

页岩气在天然裂缝系统中的连续性方程为

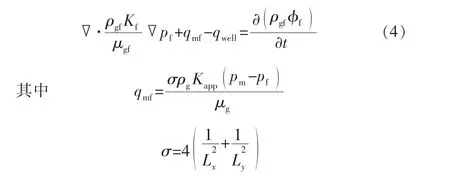
页岩储层水力压裂后，主裂缝周围的缝网一般处于未支撑或弱支撑状态，随着储层孔隙压力的下降，开启的裂缝将会逐渐闭合，表现出较强的应力敏感性。表征体积压裂区渗透率随压力变化的公式为

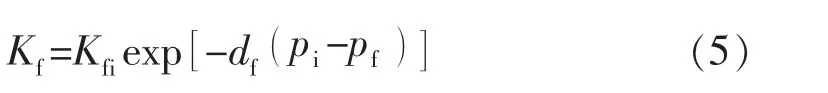
页岩气在主裂缝中的连续性方程为

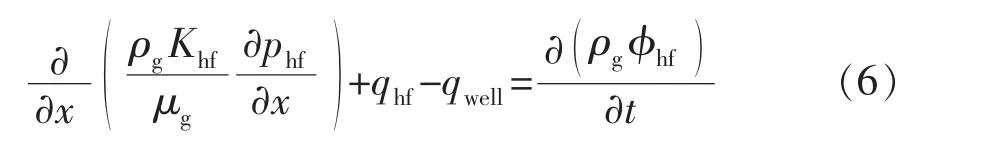
2.2 初始条件

初始条件下，基质系统和裂缝系统压力相同，均为原始储层压力：

2.3 边界条件

Γ1表示求解域外边界，Γ2表示求解域内边界。假设对于给定的研究区域外边界封闭，内边界定压，则边界条件为

3 数值离散模型

3.1 Galerkin有限元方法

将式（3）代入式（2）中，只考虑储层中流体平面二维流动，将式（2）和式（4）展开得：

其中：Cft=Cg+Cf，Cmt=Cg+Cm。

对于页岩气渗流微分方程（9），由Galerkin有限元法在单元内进行积分得［18-19］：

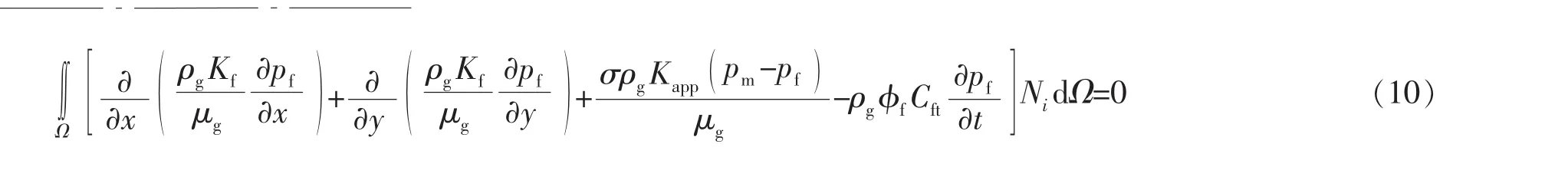
应用Green-Gauss公式得：

采用Galerkin加权残量法来推导式（14）的有限元计算格式，采用三角形单元进行剖分，设插值函数为

将式（15），（16）代入式（14）并写成矩阵形式，得：

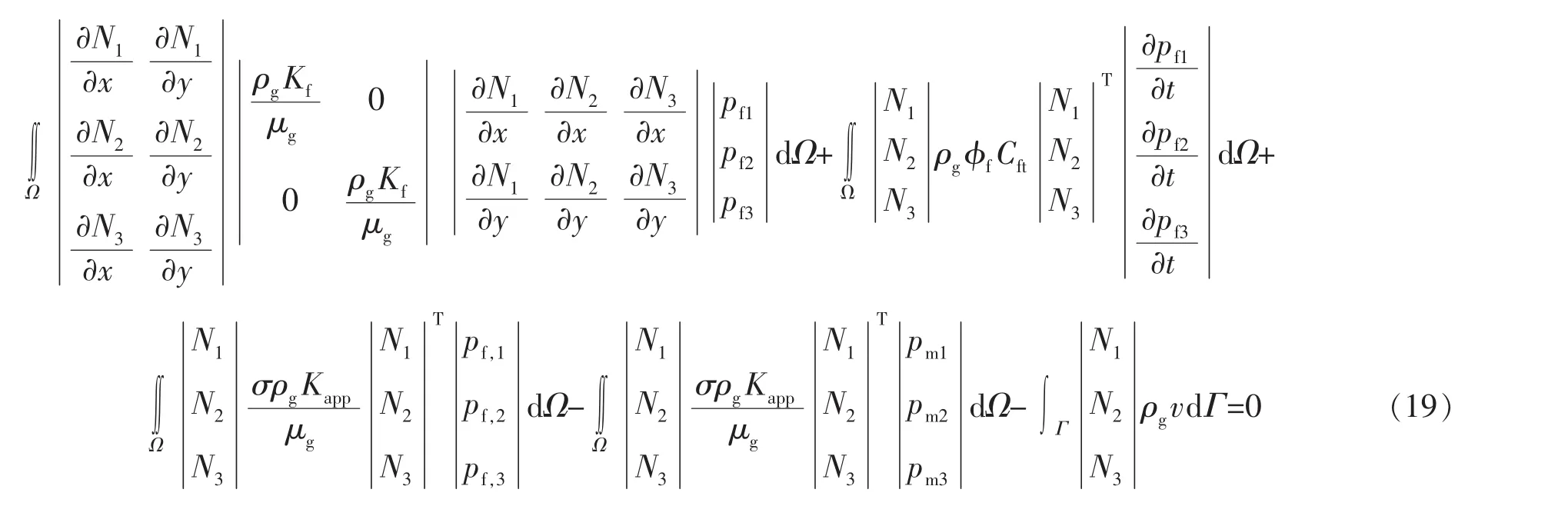
则式（19）变为

类似于裂缝系统有限元方程的推导过程，可得基质系统有限元方程：

上述单元矩阵方程Mf和Mm中，气体密度、黏度、以及基质和裂缝渗透率均是压力的函数，考虑单元内物性参数均匀。因此，可以用三角形单元形心处的值近似处理，即：

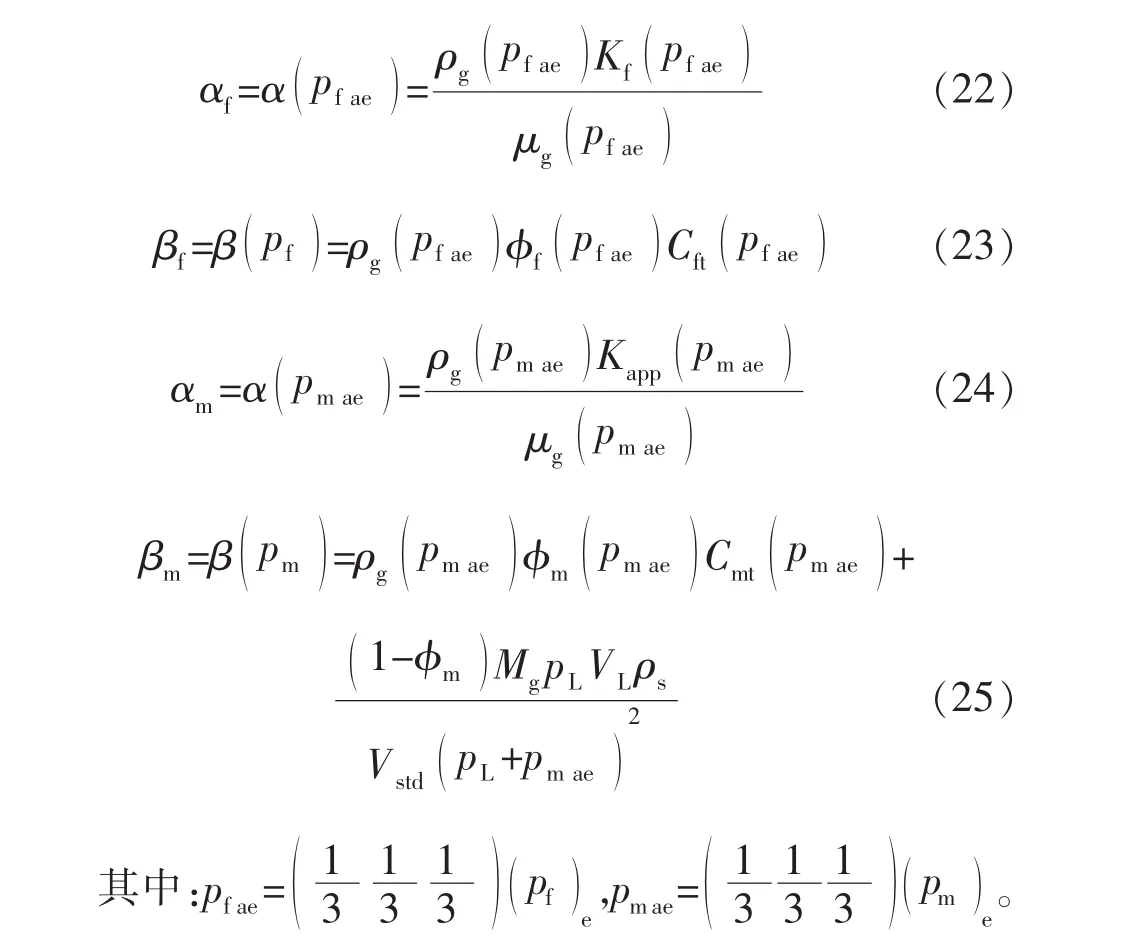
暂时不考虑方程（20）左边最后一项（即压力场边界条件影响项，将在后面进行讨论）。对时间域采用向后差分格式离散，并对与压力有关的系数进行显式处理［20］，最终得到天然裂缝系统任意单元矩阵平衡方程：

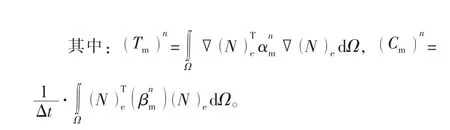
对单元有限元方程进行总体合成，获得整体的有限元方程，并引入初始条件和边界条件，在有限元整体平衡方程中，由于互含基质和天然裂缝压力项，因此，先求解裂缝系统压力方程，再求解基质系统压力方程，从而可获得地层中任一节点处压力随时间的变化规律，并求得任意时间步井底流量。

3.2 边界条件处理

对于方程（20）中边界影响项Γ∫（N）TeρgvdΓ，若单元e为不含边界的单元，则该项自然为0，单元特征分析后处理为［0，0，0］T向量。值得注意的是，对于封闭外边界，v=0，该项依然处理为［0，0，0］T向量。因此，对于内部单元和封闭外边界，该项自然为0。对于内边界，由于井筒尺寸相比整个油藏小得多，因此，根据质量守恒原理，可以将qgwell考虑为裂缝单元中的点汇项，这与采用有限差分法进行油藏模拟类似。将裂缝放宽处理并剖分为多个矩形单元，进一步将矩形单元剖分为三角形单元后，井点则位于三角形单元的某一节点上。在实际计算中，采用上一时间步的井点压力计算的点源或点汇强度，代入总刚度矩阵合成的某一裂缝单元节点上，对于定产内边界，可以直接在单元节点上加上或减去一个源汇强度。对于定压内边界：

4 实例模拟

4.1 基本参数

页岩储层厚度40 m，长度1 500 m，宽度400 m，井筒长度1 200 m，井底流压10 MPa，原始地层压力20 MPa，地层温度70℃，基质孔隙度5%，天然裂缝孔隙度0.1%，基质孔隙半径5 nm，孔隙介质迂曲度为5，天然裂缝渗透率 3×10-5μm2，水力主裂缝导流系数 0.5 μm2·cm，次裂缝导流系数 0.03 μm2·cm，缝网长 120 m，缝网宽90 m，主裂缝数10条，天然裂缝间距3 m，天然裂缝应力敏感系数0.05 MPa-1，基质压缩系数2×10-4MPa-1，天然裂缝压缩系数 0.05 MPa-1，Langmuir体积 2×10-3m3/kg，Langmuir压力 5 MPa， 页岩密度 2 600 kg/m3，甲烷分子质量16 g/mol，标准状况下页岩气摩尔体积0.022 4 m3/mol。

4.2 模拟结果分析

基于上述参数，模拟页岩气水平井体积压裂后生产5，10 a的储层压力分布（见图2），可以看出体积压裂区内的储层压力下降较多，而未压裂区的储层压力几乎没有变化，表明该时间段主要采出了改造体积内的游离气和吸附气。

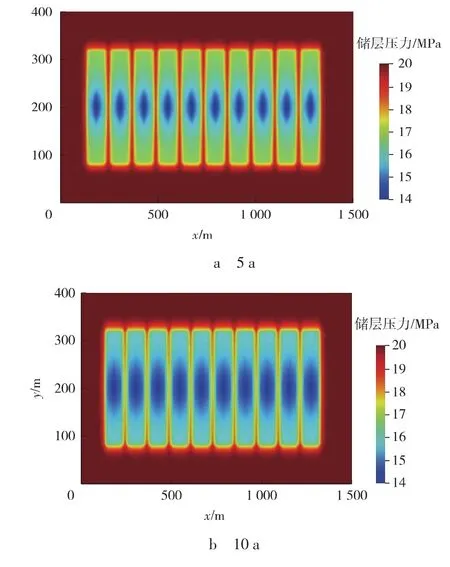
图2 页岩气生产过程中储层压力分布

图3，4为页岩储层改造体积对产气量的影响情况。由图可以看出：在其他参数相同的情况下，改造体积SRV从36×104m3增大到180×104m3， 产气量增加幅度较大；随着改造体积的增加，日产气量和累计产气量都增加，但是增加幅度逐渐变小，对于给定储层地质条件，存在最佳增产改造体积。

图3 页岩储层改造体积对日产气量的影响

图4 页岩储层改造体积对累计产气量的影响

图5是本文有限元方法与商业软件模拟产气量结果的对比（SRV=180×104m3）。由图可以看出，两者结果误差为8%，这也说明了有限元方法模拟结果的准确性，同时商业软件的模拟结果略小于有限元方法的模拟结果，这是因为本文有限元方法考虑了表观渗透率的影响。

图5 模拟结果对比

5 结论

1）基于三孔双渗连续介质模型，考虑基岩纳米孔隙中气体吸附解吸效应、Knudsen扩散和滑脱流、储层应力敏感效应，建立了页岩储层考虑复杂流动行为的动态评价数学模型。基于页岩储层体积压裂缝网扩展特征，划分了支撑主裂缝、缝网波及区和未改造区，提出了采用双重介质和离散裂缝模型描述复杂缝网的物理模拟模型。

2）推导了基于Galerkin有限元法离散的页岩气双重介质二维渗流数值模型，给出了压裂水平井内外边界处理方法，实现了应用有限元法求解页岩气压裂井产能动态和压力场分布，对于采用有限元法模拟双重介质气藏渗流场具有重要的理论意义。

3）页岩储层改造体积是影响页岩气产量的重要因素，随着储层改造体积的增大，气井产量逐渐增加，但是增加的幅度会下降。开展页岩气在多尺度储层中的复杂流动行为的研究，建立相应的产能评价模型，分析影响产能的缝网参数和储层参数对于认识完善页岩气渗流理论，弄清影响产能的主次因素，提高页岩储层体积压裂设计的科学性具有重要的理论和现实意义。

6 符号注释

Kapp为基岩表观渗透率，10-3μm2；φ为孔隙度；τ为多孔介质迂曲度；rn为页岩平均基质孔隙半径，nm；Mg为气体分子质量，kg/mol；μ为黏度 mPa·s；R 为绝对气体常数，8.314 J·mol/K；T 为绝对温度，K；ρ为密度，kg/m3；p为压力，MPa；α为切向动量适应系数，本文取值0.8；qmf为气体从基质向天然裂缝的流量，kg/（m3·s）；qa为单位体积的吸附量，kg/m3；ρs为页岩密度，kg/m3；Vstd为气体在标准状况下的摩尔体积，m3/mol；VL为Langmuir体积，m3/kg；pL为 Langmuir压力，MPa；qwell为气体从裂缝流向井筒的窜流量，kg/（m3·s）；Lx，Ly分别为基质岩块在x，y方向的长度，m；σ为形状因子；Kfi为裂缝初始条件下的渗透率，10-3μm2；df为天然裂缝应力敏感系数，MPa-1；pi为原始储层压力，MPa；qhf为气体从主裂缝向天然裂缝的窜流量，kg/（m3·s）；n 为求解域外边界曲面的外法线矢量；pwf为井底流压，MPa；Cft，Cmt分别为裂缝、 基质的总压缩系数，MPa-1；Ni为单元形函数；Γ为区域Ω的边界；QT为水平井总日产量，m3/d；W为裂缝宽度，m；req为等效井半径，m；rw为井半径，m；Bg为体积系数。下标 m，f，g，hf分别表示基质、裂缝、气体、主裂缝。

［1］ MAYERHOFER M J，LOLONE P，WARPINSKI N R，et al.What is stimulated reservoir volume （SRV）? ［J］.SPE Prod&Oper，2008，15（4）：473-485.

［2］ SWAMI V，SETTARI A T，TAVADPOUR F.A numerical model for multi-mechanism flow in shale gas reservoirs with application to laboratoryscaletesting［C］//TheEAGEAnnualConference&Exhibition incorporating SPE Europe，London，United Kingdom，2013.

［3］ CUO C H，WEI M Z，CHEN H W，et al.Improved numerical simulation for shale gas reservoirs［C］//The Offshore Technology Conference，Kuala Lumpur，Malaysia，2014.

［4］ 任岚，舒亮，胡永全，等.纳米尺度页岩储层的气体流动行为分析［J］.西南石油大学学报（自然科学版），2014，36（5）：112-115.

［5］ HATTIMGH S K F，REDDY B D.A finite element approach for modelling single-phase compressible flow in dual porosity systems ［J］.Journal of Petroleum Science and Engineering，2009，69（1）：1-24.

［6］ PARK Y C，SUNG W M.Development of FEM reservoir modelequipped with effective permeability tensor and its application to naturally fractured reservoirs［C］//The International Oil and Gas Conference and Exhibition in China，Beijing，2000.

［7］ SHENG M，LI G，SHAH S N，et al.Extended finite element modeling of multi-scale flow in fractured shale gas reservoirs ［R］.SPE 159919，2012.

［8］ BHATIA K S，ADVANI S H，LEE J K.Finite element representation of two-phase fluid flow through a naturally fractured reservoir［R］.SPE 19069，1989.

［9］ 程林松，李春兰，郎兆新.裂缝性底水油藏水平井三维油水两相有限元数值模拟方法［J］.石油勘探与开发，1998，25（2）：41-45.

［10］盛茂，李根生，黄中伟，等.页岩气藏流固耦合渗流模型及有限元求解［J］.岩石力学与工程学报，2013，32（9）：1894-1900.

［11］徐兵祥，李相方，张磊，等.裂缝性页岩气藏水平井产能预测模型［J］.中国石油大学学报（自然科学版），2013，37（6）：92-99.

［12］ ZHAO Y L，ZHANG L H，LUO J X，et al.Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir［J］.Journal of Hydrology，2014，512：447-456.

［13］ WU Y S，LI J F，DING D Y，et al.A generalized framework model for the simulation of gas production in unconventional gas reservoirs［J］.SPE Journal，2014，19（5）：845-857.

［14］ SWAMI V，CLARKSON C R，SETTARI A.Non darcy flow in shale Nan pores：do we have a final answer?［R］.SPE 162665，2012.

［15］ AZOM P N，JAVADPOUR F.Dual-continuum modeling of shale and tight gas reservoirs［R］.SPE 159584，2012.

［16］ SHABRO V，TORRES-ERDIN C，SEPEHRNOORI K.Forecasting gas production in organic shale with the combined numerical simulation of gas diffusion in Kerogen，Langmuir desorption from Kerogen surfaces，and advection in Nan pores［R］.SPE 159250，2012.

［17］董平川，牛彦良，李莉.各向异性油藏渗流的有限元数值模拟［J］.岩石力学与工程学报，2007，26（增刊1）：2634-2639.

［18］刘振宇.有限元法在油藏渗流中的理论和应用［D］.大庆：东北石油大学，2003.

［19］ 姚军，孙海，樊东艳，等.页岩气藏运移机制及数值模拟［J］.中国石油大学学报（自然科学版），2013，37（1）：91-98.

［20］黄朝琴，姚军，王月英，等.基于离散裂缝模型的裂缝性油藏注水开发数值模拟［J］.计算物理，2011，28（1）：41-49.

（编辑 孙薇）

Finite element numerical simulation of shale gas production of hydraulically fractured horizontal well with stimulated reservoir volume

HE Yidong1,REN Lan1,ZHAO Jinzhou1,LI Zhiqiang1,DENG Peng2
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China;2.Tazhong Oil and Gas Development Department,Tarim Oilfield Company,PetroChina,Korla 841000,China)

Affecting by multiple composite effects,shale gas reservoirs with complex fracture-network were divided into propped primary-fracture,stimulated area and unstimulated area.Considering adsorption and desorption of shale gas in matrix porosity,Knudsen diffusion,slippage effect,viscous flow,stress sensitivity of natural fractures,corresponding physical model for production simulation of volume fracturing and mathematical model of shale gas flow after hydraulic fracturing were established.Galerkin finite element has been used to discretize seepage equations for natural fracture and matrix with only taking two-dimensional flow into consideration.Finite element equation based on triangular element was derived,we also give the method for handling the boundary condition with considering two-dimensional seepage field for fractured horizontal well and main hydraulic fracture;backward difference was employed for time domain discretization,and pressure equation of matrix and fracture systems were solved sequentially to model pressure field and production of shale horizontal well with stimulated reservoir volume.This study provides a theoretical model for the evaluation of the volume fracturing of shale gas reservoirs,which has important theoretical and practical significance for the finite element method to simulate the flow field of the double porosity reservoir.

shale gas;volume fracturing;dual continuum;finite element;production simulation

TE357

A

国家自然科学基金青年科学基金项目“基于多尺度页岩复杂流动行为的动态评价模型研究”（51404204）；国家科技重大专项“涪陵页岩气开发示范工程”（2016ZX05060）；中国石油化工股份有限公司项目“裂缝动态扩展影响因素研究”（31400026-16-ZC0607-0013）

10.6056/dkyqt201704025

2016-12-23；改回日期：2017-05-20。

何易东，男，1993年生，在读硕士研究生，主要从事油气田增产改造技术研究工作。E-mail：heyidong1993@163.com。

任岚，男，1979年生，副教授，2003年毕业于西南石油学院石油工程专业，主要从事油气田增产改造技术研究工作。E-mail：renlanswpu@163.com。

何易东，任岚，赵金洲，等.页岩气藏体积压裂水平井产能有限元数值模拟［J］.断块油气田，2017，24（4）：550-556.

HE Yidong，REN Lan，ZHAO Jinzhou，et al.Finite element numerical simulation of shale gas production of hydraulically fractured horizontal well with stimulated reservoir volume［J］.Fault-Block Oil&Gas Field，2017，24（4）：550-556.