具有连续时滞的微分方程的概周期解

严建明

（湖南财政经济学院基础课部，湖南长沙410205）

具有连续时滞的微分方程的概周期解

严建明

（湖南财政经济学院基础课部，湖南长沙410205）

结合运用Liapunov泛函数，研究Lotka-Volterra系统的概周期解的存在唯一性和一致渐近稳定性.关键词：连续时滞；竞争系统；Liapunov泛函；概周期解

众所周知，在种群动力学的研究中，生物种群的持续生存是数学生态学中捕食与竞争理论及其相关课题的一个重要而广泛的、且受到人们非常关注的课题.1965年，Holling在实验的基础上，对不同的物种，提出了三种不同的功能性反应函数.对具有Holling I、II、III类功能性反应的系统，许多学者进行了深入研究[1，2].由于概周期现象在实际问题中经常可见，以周期现象作为特例，它是比周期现象更广泛的现象。对于Lotka-Volterra系统的概周期解的定性性质（概周期解的存在唯一性和一致渐近稳定性）的研究工作目前相对还较少[3-6].而对于同时具有连续时滞、扩散、HollingⅡ类功能性反应的Lotka-Volterra型竞争系统的研究非常少.本文研究如下的具有连续时滞、扩散、HollingⅡ类功能性反应的非自治竞争模型：

在本文中，我们采用如下记号和概念.

代表欧几里德范数）的非负连续函数构成的Banach空间.因此，如果我们选C+为系统（1）的初始函数空间，易知对坌准=（准0，准1，准2）∈C+且准（0）＞0，则系统（1）在[-τ，∞）上存在唯一解x（t，准），且对于t∈[0，+∞）有x（t，准）＞0，我们称此解为系统（1）的正解.因此，在本文下面的研究中，我们总假定

对于系统（1），记x（t）=x（0，准）（t）是过（0，准）的解，其中初值函数.则x（t）是唯一的，且x（t）＞0，t∈[0，T），这里[0，T）是系统（1）的解的最大存在区间，这样的解叫做系统（1）的正解.

引理1[7]考虑泛函微分方程

及乘积系统

这里总是假设0＜H*＜+∞，f∶R×C→R3对φ关于t是一致概周期的，若存在连续函数V∶R+×S×S→R+，满

H*H*H*足如下条件：

（Ⅰ）a（|x-y|）燮V（t，x，y）燮b（|x-y|），其中a（s），b（s）∈CIP，b（0）=0；

（Ⅲ）存在连续非减函数p（s），当s＞0时，有p（s）＞s，使得当

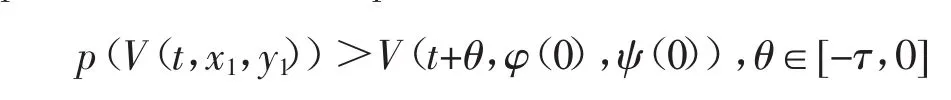
时有D+V（t，φ（0），ψ（0））燮-cV（t，φ（0），ψ（0）），c＜0是常数.

如果系统（5）的每一个解满足‖ξ（t）‖燮-cV（t，φ（0），ψ（0）），t叟T0，那么系统（5）必存在一致渐近稳定的概周期解，进而如果（ft，φ）关于t是ω周期的，则系统（5）存在一个周期解，且是全局渐近稳定的.

定理设系统（1）满足以上给定的条件（2）（3），且还满足

证明考虑系统（1）的乘积系统

定义集合

可知Ω*是系统（7）的最终正向不变集.

在Ω*上定义Liapunov函数为

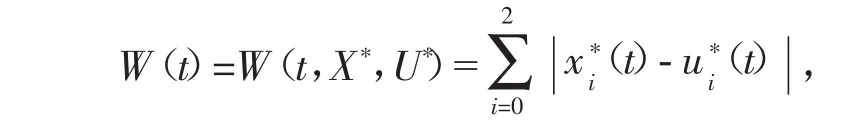
对于乘积系统（9）在Ω×Ω上的任一解

因为

其中ξ（t），η（t）分别位于lnm1与lnM1之间及lnm与lnM之间.

则得到

则

从而由条件（8）可知存在常数使得有

由引理1知，系统（1）在区域Ω中存在一致渐近稳定的概周期解，进而如果系统（1）的右端关于t是ω-周期的，则系统（1）存在一个ω-周期解.

[1]靳祯，原三领，马知恩.具有功能性反应的三种群食物链系统全局周期解的存在性[J].工程数学学报，2001，18（4）：69-75.

[2]桂占吉，陈兰荪.具有功能性反应的非自治竞争系统持续性[J].工程数学，2001，17（2）：7-10.

[3]罗桂烈.具时滞的非自治扩散捕食系统的概周期解[J].生物数学学报，1998，13（1）：32-38.

[4]罗桂烈，廖民锂，江佑霖.两种群非自治Lotka-Volterra竞争扩散系统的概周期解[J].系统科学与数学，1998，18（2）：204-210.

[5]Zhang Jingru，Chen Lansun.Periodic solutions of single-species nonautonomous diffusion models with continuouse time delays[J].Math. comput.modelling，1996，23（7）：17-27.

[6]杨启贵，江右霖.Willis环状脑动脉瘤模型的概周期解[J].生物数学学报，2000，15（3）：313--318.

[7]Yuan Rong.Existence ofalmost periodic solution offunctional differential equations[J].Ann.ofDiff.Eqs.1991，7（2）：234-342.

On almost Periodic Solution of Differential Equations with Continouous Time Delay

YAN Jian-ming
（Dept.of Basic Subject，Hunan University of Finance and Economics，Changsha，Hunan 410205）

In this paper，the existence，uniformly asymptotical stability of almost periodic solutions was considered by using Liapunov functional.

continouous time delay；competition system；liapunov function；almost periodic solution

O175

A

1671－9743（2017）05－0028－04

2016-09-21

严建明，1974年生，男，湖南益阳人，讲师，研究方向：微分方程.