基于方差分析与主成分分析下的教育指标评价应用
——以上海市2015年“绿色指标”为例
2017-07-21汪慧玲
汪慧玲
(咸宁职业技术学院 工学院,湖北 咸宁 437100)
基于方差分析与主成分分析下的教育指标评价应用
——以上海市2015年“绿色指标”为例
汪慧玲
(咸宁职业技术学院 工学院,湖北 咸宁 437100)
在统计学中,方差分析用于检验各因素间显著性水平,主成分分析用于生成相互独立的组合变量,便于实际分析需求。在新课程背景下,教育学中的理论研究与教学实践反馈相结合,为完善教育理论体系,提供有力的数据基础与理论保证。本文主要基于方差分析与主成分分析,结合教育实际案例,对相关教育评价指标体系作出科学评估与反馈。
方差分析;主成分分析;教育指标
作为统计学与数学应用的重要组成部分,方差分析与主成分分析广泛应用于显著性测评与影响因素管控等方面。近年来,随着教育的不断发展,各地的教育研究学者都相继提出不同教育评价指标体系。本文主要基于数学中方差分析与主成分分析等方法,以上海市2015年提出的“绿色指标”为例,结合某小学实际案例分析,从数学应用出发,作出关于教育评价指标体系科学性的评价与检验,同时也为继续发展和完善相关教育指标体系提供新的思路与方法。
一、关于方差分析与主成分分析
(一)方差分析
1.方差分析简介
方差分析(Analysis of Variance),简称ANOVA,又称为“变异数分析”或者“F检验”,是R.A.Fisher发明的用于两个及以上样本均数差别显著性检验的方法。由于各种因素的共同影响,研究所得的数据呈现波动状,而造成波动的原因可以分为两大类:一类是不可控的随机因素,另一类是研究中的相关可控因素对结果形成的影响。
方差分析是从观测变量的方差着手,去研究诸多控制变量中对观测变量有显著性影响的相关变量。方差分析可分为单因素方差分析与多因素方差分析。
2.方差分析的作用
方差分析的主要作用有:(1)均数差别的显著性检验,(2)分离各有关因素并估计其对总变异的作用,(3)分析因素间的交互作用,(4)方差齐性检验,等等。
在实际研究中,针对一个复杂的事物体系,其中往往有许多因素相互制约又相互依存。方差分析的目的就是通过数据分析,找出对该事物体系有显著影响的因素,各因素间的交互作用,以及显著性水平等。方差分析在可比较数组中,将数据总的变差,并对变差的度量采用离差平方和,来按照各指定变差来源进行分解处理。
3.方差分析的基本步骤
(1)前提假定
1)各处理条件下的样本随机;
2)各处理条件下的样本相互独立;
3)各处理条件下的样本分别来自正态分布总体;
4)各处理条件下的样本具有齐效性。
(2)基本步骤
Step 1:建立假设检验(H0:各样本总体均值相等,H1:各样本总体均值不全等,检验水平α一般默认为0.05);
Step 2:计算检验统计量F值;
Step 3:确定P值并作出结果评价。
(二)主成分分析
1.主成分分析简介
主成分分析(Principal component analysis)是采取一种数学降维的方法,找出几个综合变量来替代原来众多的原始变量。这些综合变量尽可能的代表原始变量的信息表达,同时彼此间做到互不相关性。这种将多个原始变量转化为少数几个相互独立的综合变量的统计分析方法叫做主成分分析或者主分量分析法。
2.主成分分析的作用
假设X=(x1,x2,…,xp)T是一个p维的总体,X的期望E(X)和协方差矩阵cov(X)已知,则我们求解协方差矩阵的p个特征值,不妨记为:λ1≥λ2≥…≥λp≥0
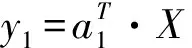
3.主成分分析的基本步骤
Step 1:对原始数据作标准化处理,设样本观测数据矩阵为:
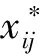
其中,

Step 2:计算样本相关系数矩阵R,
其中,为简便记,假定原始数据标准化后矩阵仍为X,此时有:
Step 3:用Jacobi方法求相关系数矩阵R的特征值(λ1,λ2,…,λp)与相应特征向量
ai=(ai1,ai2,…,aip),i=1,2,…,p;
Step 4:选择重要的主成分,并写出主成分表达式,其中:
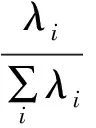
Step 5:计算主成分得分矩阵F(k为主成分个数),则有:
Step 6:依据主成分得分数据,可进行进一步统计分析。
二、关于“绿色指标”体系
(一) “绿色指标”的总体概述
1.实施“绿色指标”评价体系的重要性
(1)“绿色指标”有利于发挥科学教育评价的正确导向作用,引导学校、家长和社会树立全面的教育质量观,丰富学业质量评价的内涵,引导学校开展全面质量观指导下的教学与评价活动,减轻学生课业负担,促进学生全面发展。
(2)“绿色指标”有利于构建教育内部“标准—教学—评价”的良性循环系统,指导学校建立以校为本、基于过程的教育质量综合评价体系,营造有利于学生健康成长的良好氛围,促进教育质量持续提高。
2. “绿色指标”的主要内容和测评手段
(1)指标内容:包括学生学业水平指数、学生学习动力指数、学生学业负担指数、师生关系指数、教育方式指数、学生社会经济背景对学业成绩的影响指数、学生品德行为指数、身心健康指数、校长课程领导力指数与学生跨年度进步指数,共十个方面。本次数据评估,只选取前八个指数参与测评与分。
(2)测评手段:学业测试水平(小学生测试语文、数学,初中生测试语文、数学、外语等学科)、问卷调查(以学生为主,兼顾教师、校长)等。
(二)关于“绿色指标”的具体参数
“绿色指标”主要包括以下具体指数,并构成三层指标体系(指标-指数-因子),如表1所示:

表1 绿色指标三层架构分类
三、基于数据的评价反馈
(一)主要流程
本次数据采集对象均来源于湖北省武汉市洪山区武珞路小学2015-2016学年第一学期三年级(共7个班级)与五年级(共6个班级)的全体在校学生。具体数据分为:(1)2015-2016学年第一学期三年级与五年级全体在校学生的期中测验有效成绩记录,数据由校方提供,并将数据按照一定的百分比(原则上人数前20%为一类,后20%为一类,剩余为一类)(2)以上全体学生参与的《武珞路小学关于“绿色指标”的问卷调查表》其中的有效问卷数据记录,问卷由校方代为分发收集,供于非直观量化评价因子的数据采集与分析。
本部分基于武汉市某小学三年级段在2015-2016学年第一学期的学测成绩与问卷调查结果的统计分析,运用“绿色指标”评价体系,对该年级师生作出新的一轮评价,并分析学生学业成绩与其余指标间的显著性水平[1]。
本部分主要采用方差分析与主成分分析法,采用的分析软件主要有:IBM SPSS Statistics 20与MATLAB 2007b等。
(二)学生基本信息
1.年级基本概况
本年级共有学生334人,有效成绩记录332人,有效问卷调查数据316人。
2.成绩基本信息统计
本次期中测试共有332人参加,语文平均为91.4分,成绩及格率为100%。数学平均为92.6分,成绩及格率为100%。其余信息详见以图2所示:
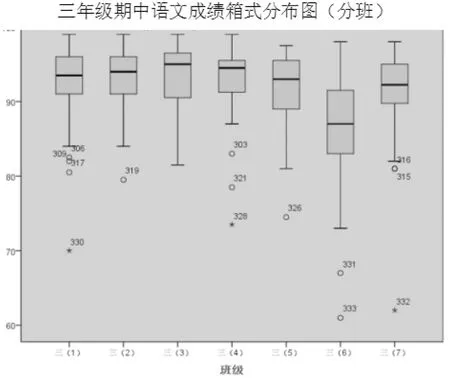
图2 三年级期中语文成绩箱式分布图
3.非成绩基本信息统计
本次问卷调查共有316人有效参与。问卷部分数据有缺损,不作为作废标准。各题情况与初步分析见以图3~4表示:
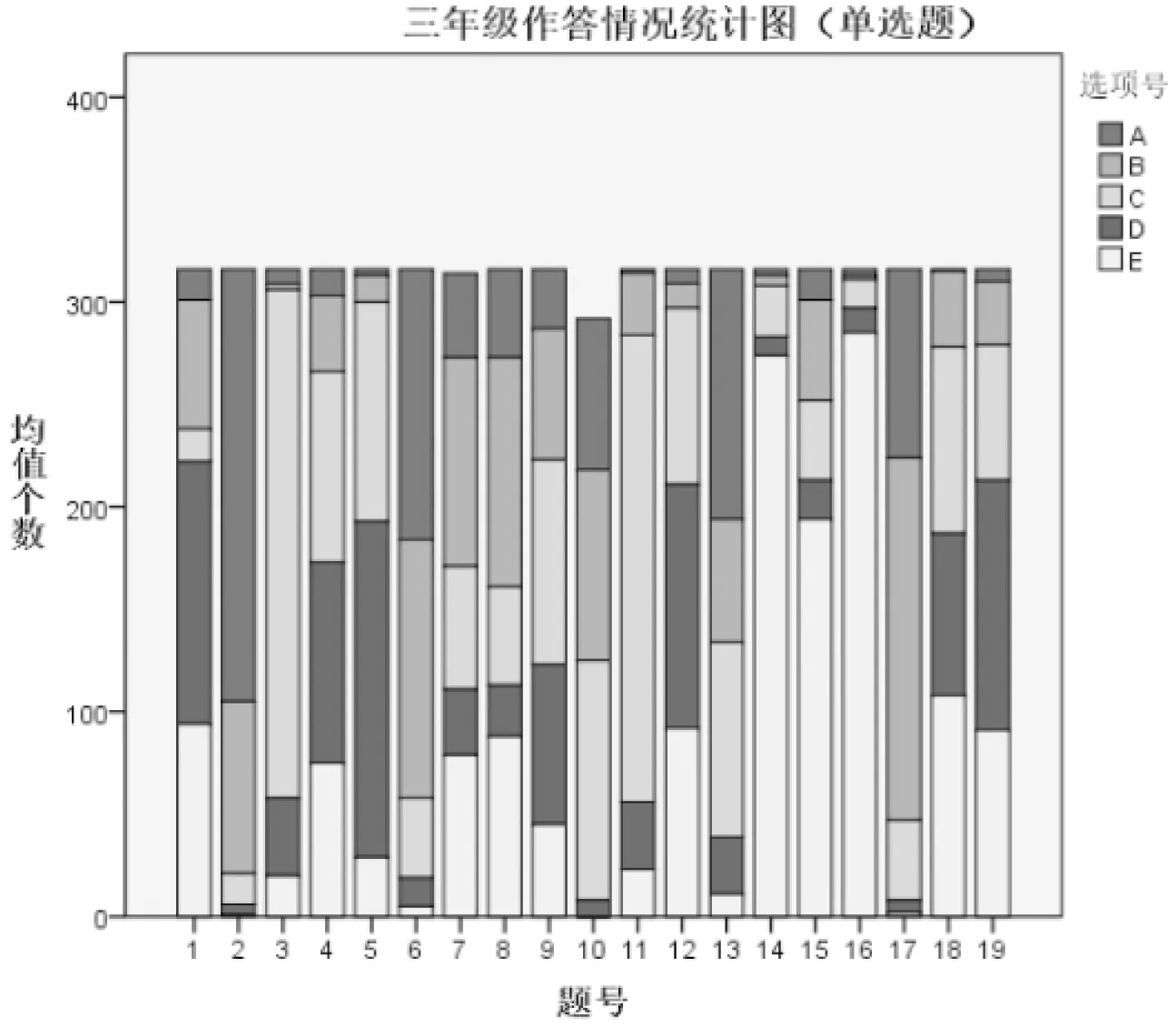
图3 三年级作答情况统计图(单选)
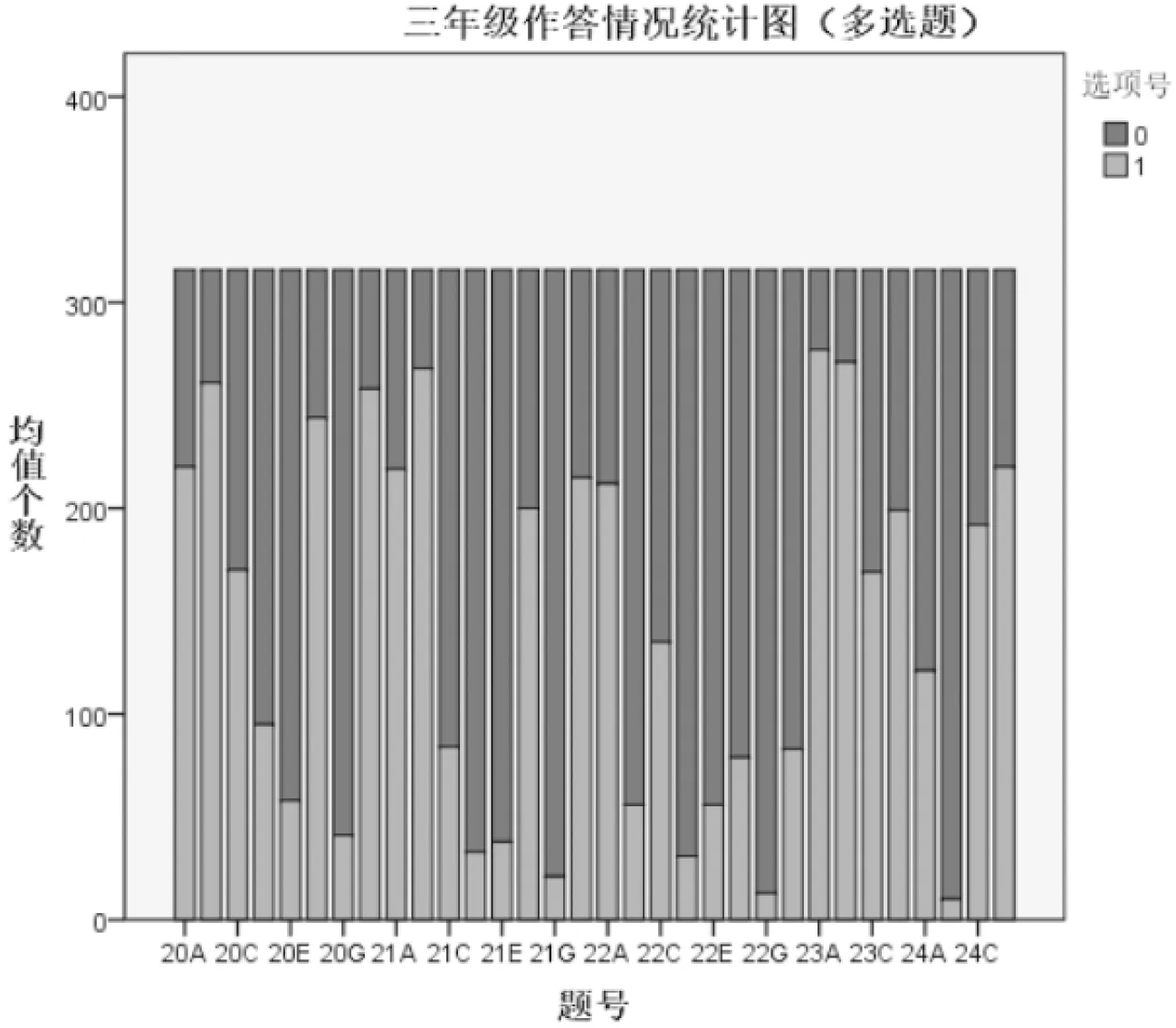
图4 三年级作答情况统计图(多选)
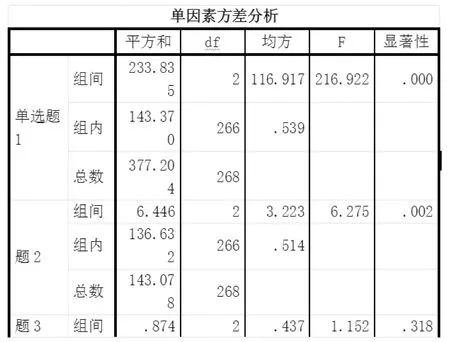
图5 单因素方差分析
(三)方差分析
1.明确目的
我们通过方差分析,得出单纯依靠成绩衡量学生标准下的“好与坏”,在新型建立的“绿色指标”教育评价体系下的更多相关因素,以探讨学生学业成绩水平的综合因素。
2.统计分析
我们对本年级学生学业水平指数(即成绩因子)与问卷调查因素(如上所示)的关联性加以分析,试图找出成绩与其它因素的相关性,并给出指导性建议[2]。我们采用各因素方差分析的方法,具体如图5所示。
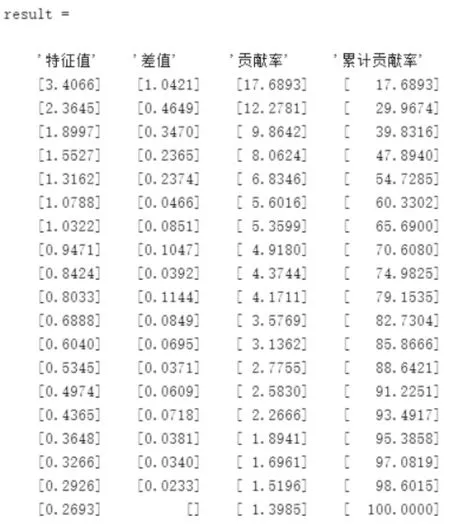
图6 各因素主成分分析
3.相关分析
我们选择的显著性为0.05,即置信度为95%。关注图表中的sig.指数,其中:
单选题01,04,12,13,15,18,19的sig<0.01,说明以上单选题与学生分类显著相关;
单选题02,03的sig<0.05,说明以上单选题与学生分类有相关性。
4.相关结论
(1)在三年级中,学生成绩的好坏,与学生的自信心,学生的自我认同度有关联。通过对数据的分析,一般地,成绩好的学生有较大自信,自我认同度高;成绩中等的学生,自信心与自我认同度会较之下降;成绩较差的学生,自信心与自我认同度较低;
(2)在三年级中,学生成绩的好坏,与学习动力、往次成绩对自身的影响因素有关;其中,成绩较好的学生,学习动力越强,也较看重往次成绩,对自身影响较大;反之亦然;
(3)在三年级中,学生成绩的好坏,与家庭和谐因素有关;其中,学生成绩较好,家庭较为和谐;反之,学生成绩较差,家庭和谐程度也较为低迷;
(4)在三年级中,学生成绩的好坏,与学生尊重与责任心有关,且成正相关:学生成绩较好,相应尊重与责任心表现也越好;
(5)在三年级中,学生成绩的好坏,还与学生锻炼与幸福指数相关,且呈正相关:学生成绩较好,相应的锻炼积极性与幸福感表现也较好;反之亦然。
5.相关评价
通过进行方差分析,我们可以得出以下结论:
(1)学生学业成绩(即分数)的高低与“绿色指标”评价体系中的因素有相关性,部分指标显出的显著性较强;
(2)存在部分指标是各类学生都具有共性的,或者分布较为均匀的;
(3)我们在教育中,应重视显著性较强的相关指标,在日常的教育中有所体现和侧重,并建立更为科学合理的评价标准,因材施教。
(四)主成分分析
1.明确目的
我们通过主成分分析,可以优化现有的“绿色指标”评价体系,使得评价指标更简洁,更精准,更具有相互独立性。
2.统计分析
我们对除学生学业水平指数(即成绩因子)外的其余19个单选研究指数做主成分分析[3],并得出主成分指标,以便进行进一步的有效研究。详见上图3-5所示。
此分析中不可允许NaN或者Inf,故我们采用平均取值的方法补齐为数不多的缺损值。
3.相关分析
主成分分析旨在找到分析问题的主要指标因素,在本年级数据中,由图6可知,取前12个主成分,其累计贡献率达85%,即其代表率达85%,即可符合要求。
四、结语
在当今“育人为本,教育为先”的背景下,用适合学生全面发展的教育评价体系来代替以往“唯成绩论成败”的评价标准,是一种势在必行的趋势和发展方向。面对各种教育评价体系的提出与实践,我们更加需要用一种科学严谨的态度,去反复的跟踪论证它的科学性与可行性。
本文中主要运用的方差分析与主成分分析法,则为我们提供了对教育评价体系作出效能评估的有力方法,它使得我们去评价一种体系时,有理有据,从理论中来,到教学实践中去,最后再反馈和修正机制,使得更加科学完善。
同时,关于“绿色指标”评价,应根据各个学校的实际情况,选择主要影响因素来分析学生、教师、家庭、学校、社会等方面的相互影响性。对于“绿色指标”评价体系而言:一方面,要关注普遍倾向性明显的作答情况,此说明学生与家庭的普遍诉求与愿望;另一方面,要重点关注某些因素(如学业水平因素)与其余某些因素之间的关系,以作为“绿色指标”的重要应用之一。针对后续规划,我们可以进一步分析其余因素间影响,优化问卷调查形式及内容,保证进行的客观性,持续关注效果反馈等。
将数学统计分析应用于教学评价中,无疑为我们得出的结论提供了强有力的保障,使得我们在教育改革的路上,走得自信,科学,可持续发展。
[1] 薛薇.统计分析与SPSS的应用(第4版)[M].北京:中国人民大学出版社,2014.90~97.
[2] 赵东方.数学模型与竞赛[M].武汉:华中师范大学出版社,2014.50~70.
[3] Rick Durrett.Probability:Theory and Examples[M].Oxford:Cambridge University Press,2010.20~22.
责任编辑:熊 瑛
2017-01-12
2095-4654(2017)03-0148-05
O212.4
A
