水平采空区群动力响应的类非线性振动模型
2017-07-21姜立春曾俊佳吴爱祥
姜立春,曾俊佳,吴爱祥
水平采空区群动力响应的类非线性振动模型
姜立春1, 2,曾俊佳2,吴爱祥3
(1. 华南理工大学土木与交通学院,广东广州,510640;2. 华南理工大学安全科学与工程研究所,广东广州,510640;3. 北京科技大学土木与环境学院,北京,100083)
在线性多自由度振动模型的基础上,考虑到围岩对水平采空区群的水平地应力作用及能量耗散影响,引入水平地应力因子和类非线性因子,建立适用于水平采空区群的类非线性多自由度振动模型。基于单个间柱微差爆破及间隔间柱单段爆破2个算例,对类非线性多自由度振动模型的合理性进行验证。研究结果表明:水平地应力未对水平采空区群的动力响应造成明显的影响,可忽略水平地应力的作用(=0);采用标准动载荷()计算水平采空区群各岩体的类非线性因子是可行的,对于同一矿山,只需计算1次,便可应用到类似工况,节省了的取值时间;对比线性模型,类非线性振动模型结果与数值模拟结果更加吻合,较好地揭示了水平采空区群各岩体的动力响应规律。
岩体力学;水平采空区群;动力响应;多自由度振动模型;水平地应力;能量耗损
金属矿体在地下空场法开采过程中形成大量采空区,同时也遗留下大量顶(底)板和间柱残矿资源。在间柱残矿进行爆破作业时,较多关注间柱本身或其相邻空区岩体的单体稳定性,而忽略了爆破作业对空区群岩体整体稳定性的影响。目前,动载荷下采空区群的力学响应规律尚处于探索阶段,揭示采空区群的动力响应特性规律,分析采空区群的稳定性并提出控制技术措施,是矿业界亟待解决的难题。现阶段,采空区(硐室)群岩体的动力响应特性主要通过数值模拟的方法获得。闫长斌等[1]利用FLAC3D研究了不同爆破荷载特性(速度、频率)和空区间距对竖向采空区群的力学响应规律及其稳定性。隋斌等[2]利用FLAC3D软件对地震荷载作用下某地下硐室群围岩的动态响应进行了模拟。吕涛等[3]基于显式有限差分方法建立了二维及三维数值模型,对溪洛渡地下硐室群的动力时程响应和地震安全性进行了分析与讨论。鲁文妍等[4]结合ABAQUS隐式和显式分析,对硐室群在地震作用下的动力时程响应进行了仿真研究。此外,也有学者借助传递函数[5]、加卸载比[6]、小波包[7]等方法对采空区的动力响应特性进行研究,并取得了一定的成果。线性多自由度振动模型源于振动力学,其建立直观、简便,可以用于描述连续体的动力响应特性[8−9],是结构动力分析的基础。本文作者将线性多自由度振动模型引入到水平采空区群动力响应研究中,根据矿山实际情况对线性振动模型进行改进,提出了适用于水平采空区群的类非线性振动模型。针对某地下矿山水平采空区群间柱残采工程,采用类非线性模型对各岩体进行动力响应分析,借助数值模拟并通过与线性模型对比,对类非线性模型的合理性进行了验证,为采空区群的动力响应研究提供一种新方法。
1 类非线性多自由度振动模型
1.1 振型截断
采空区岩体呈连续分布,属于无限自由度系统,具有无限多个自振频率。每个自振频率对应一种特定的振型,不同的振型对岩体振动产生不同的影响。
岩体受动载荷作用后,高阶频率一般不参与到动力反应中,或高阶频率引起的振型幅值相对于低阶频率在绝对值意义上是可以忽略的。原因有3个:1) 动荷载的局限性。振幅、频率和持时等动力特性不能满足岩体产生连续高频率振动的条件;2) 内部阻尼的作用。岩体发生振动时其内部孔隙的张开闭合以及其变形时产生的内摩擦,使能量以热能的形式迅速耗散,高频率振动分量快速减弱;3) 外部阻尼的影响。部分能量会耗散在周边围岩中,使高频率振动分量更快地衰减。
因此,动载荷作用下岩体发生高阶频率振动状况可忽略,可采用振型截断的方法,利用前几阶较低的自振频率进行系统动力响应的近似分析。
1.2 模型构建
将水平采空区群岩体划分为图1所示的分布结构。当水平采空区群岩体发生水平振动时,受到动荷载、重力和周边围岩剪切力等外力作用(图2)。其中,重力对岩体的水平振动未做有用功,可忽略其影响。
由于地应力的影响,水平采空区群受到围岩的水平挤压,顶(底)板岩体处于水平受压状态。另外,从能量的角度来看,因能量的衍射作用,动载荷除了给水平采空区群岩体提供振动的能量,还在围岩中耗散了部分能量。
基于上述考虑,在模型中引入水平地应力因子(≥0)和类非线性因子(≥1)。前者表示使模型左右固定边界相向靠近,各弹性元件处于初始受压状态,各质量惯性元件的和应力为0;后者则表示增加岩体内部阻尼等效内外部阻尼的共同作用。

图1 水平采空区群结构分布图
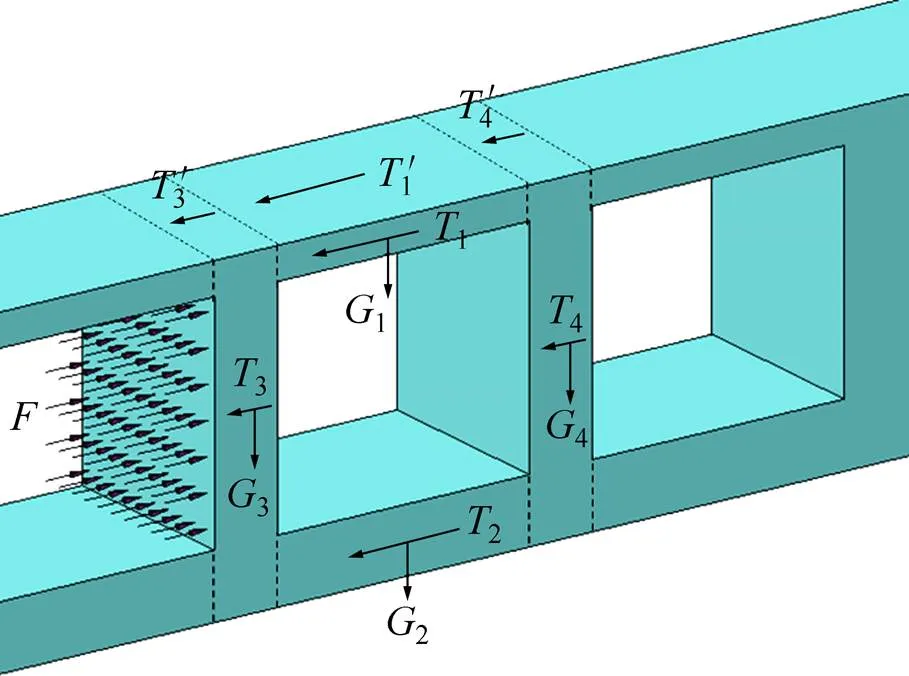
图2 单元采空区力学分析
根据各岩体在水平方向相互作用方式,建立由(≥3)个单元空区组成的水平采空区群多自由度振动模型(图3),其中,顶(底)板及间柱各等效成一个质量惯性元件,各质量惯性元件之间用无质量的弹性元件和代表能量损耗的阻尼元件连接,模型两端边界采用已压缩的固定边界。
根据牛顿第三定律及达朗贝尔原理,由个单元空区组成的水平采空区群动力平衡方程为

式中:,,,,,分别为质量矩阵、阻尼矩阵、刚度矩阵、动载荷矩阵、剪切力矩阵及类非线性矩阵;+为考虑水平地应力的位移矩阵,和分别为加速度列向量、速度列向量。其中,类非线性矩阵中的各元素只与阻尼矩阵的对应元素相乘;位移矩阵+的对角元素中为0,并与的对应元素相乘。+,和的表达式分别为
(2)
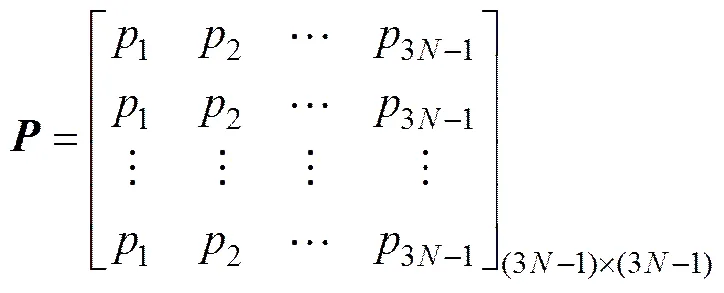
(4)
1.3 参数确定
1.3.1 刚度系数
弹性元件的刚度系数为二分之一跨度顶(底)板的水平方向刚度,即

式中:1为顶(底)板弹性模量;1为顶(底)板水平方向横截面积;为顶(底)板跨度。
1.3.2 阻尼矩阵
阻尼反映了岩体内多种耗能因素的综合影响,一般通过结构原位振动试验的方法获得[10−11]。在动力反应问题中,一般采用理想化的方法将黏性阻尼等效为实际阻尼。工程界常用的黏性阻尼为瑞利阻尼[12],如下式所示:
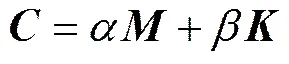
式中:和分别为质量阻尼比例系数和刚度阻尼比例系数。
当自振频率为时,阻尼比ζ为

实际工程中,通常取岩体阻尼比为0.05,则和为
(8)
考虑到自振频率带来的阻尼误差,ω和ω应选取第1阶和第3阶自振频率(即振动可能覆盖的低阶自振频率)进行阻尼系数的计算。
1.3.3 剪切力
岩体的剪切力为

式中:2为顶(底)板和间柱的剪切模量,2=1/[2(1+)];2为顶(底)板和间柱与围岩的接触面积;为顶(底)板的跨度或间柱的宽度;负号表示与位移方向相反。
1.3.4 水平地应力因子
建立由3个单元空区组成的水平采空区群二维数值模型(图4),单元空区长为40 m,间柱高为30 m,宽为10 m,岩体力学参数参照文献[13]。
图中空区采用增量法依次开挖,模型四周设置自由场边界,顶部设置自由边界,底部设置静态边界。引入标准动载荷()=5 000sin(10π),并施加到间柱1个侧面上。选取无地应力、顶部施加均布载荷为0,5,10和15 MPa等不同地应力5种工况,得到监测点在不同工况下的位移响应时程曲线,同时对方框中的曲线局部放大,见图5。

图3 水平采空区群多自由度振动模型
从图5(a)可以看出:水平地应力对水平采空区群的影响不明显,同一时间的位移相差不超过1.64%,可忽略水平地应力的影响,即=0。数值模拟过程中,可忽略地应力的作用。

图4 3个单元空区组成的水平采空区群二维数值模型

(a) 位移响应曲线总体图;(b) 位移响应曲线局部放大图
1.3.5 类非线性因子
根据前面分析,水平采空区群多自由度振动模型可忽略水平地应力因子,因此式(1)可只考虑围岩耗损的影响,经简化得

类非线性因子的计算步骤为:
1) 分别建立线性多自由度振动模型(即各岩体=1)和相应的数值模型(不考虑地应力作用);
3) 对于岩体,初始取p=1,若d<D,则直接输出p;若d>D,令p=×(和为正整数,越小,p取值越精确,但计算量越大),不断增加以增加p,直至d<D时,输出p。
需要注意的是,计算岩体的p时,应考虑之前所计算的1,2,…,p−1对p的影响,因此需保留1,2,…,p−1。类非线性因子的计算流程如图6所示。

图6 类非线性因子p计算流程
2 工程算例
2.1 算例1
取某地下矿山中由3个单元空区组成的水平采空区群进行分析(图7)。矿房长度为40 m,矿体厚度为30 m;单元空区顶板厚5 m、底板厚10 m;间柱宽10 m,高35 m。岩体力学参数见表1。为回收间柱1残矿资源,采用削柱法对间柱1侧面进行爆破作业。
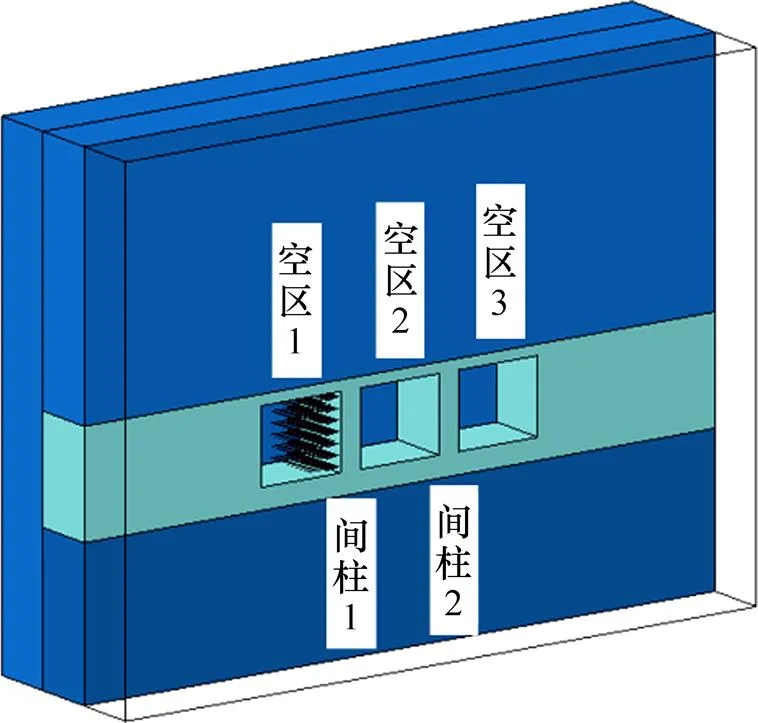
图7 3个单元空区组成的水平采空区群数值模型
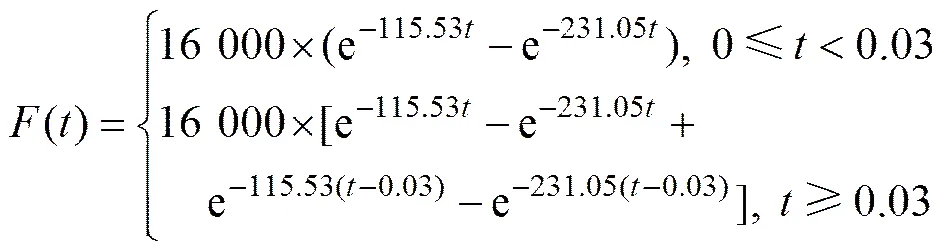
在数值模拟中,忽略地应力和模型顶部荷载的影响。根据类非线性因子的计算流程,在间柱1侧面施加标准动载荷(),考虑到p需满足较高的准确性和较少的计算量的要求,取=5,得到各岩体类非线性因子为(30,35,1,40,45,75,55,60)。将各岩体的线性模型、类非线性模型结果与数值模拟的平均结果进行对比,对比结果如图8所示。
由图8可知,数值模拟中,间柱1、空区1顶板和空区2底板产生了2次位移峰值,且第2次峰值小于第1次峰值;间柱2与空区3顶板速度则呈现幅值衰减的响应规律,最后达到平衡状态。对于类非线性模型,间柱1位移、间柱2速度与空区3顶板速度具有与数值模拟类似的响应规律,而空区1顶板和空区2底板的位移响应趋势上与数值模拟结果存在一定的差别。
对比线性模型,类非线性模型曲线在动力响应极值上与数值模拟结果具有较高的吻合性,较好地反映了水平采空区群的动力响应规律。

表1 岩体力学参数

(a) 空区1顶板位移时程曲线;(b) 间柱1位移时程曲线;(c) 空区2底板位移时程曲线;(d) 间柱2速度时程曲线;(e) 空区3顶板速度时程曲线
2.2 算例2
取同一地下矿山中由5个单元空区组成的水平采空区群进行分析(图9)。空区尺寸和岩体力学参数与算例1相同。为回收多个间柱残矿资源,同时对间隔的间柱1和间柱3进行单段爆破作业,单位面积爆破等效荷载(kPa)为

间隔间柱单段爆破可等效为2个间柱单独爆破作用的叠加,爆破交叉影响的各岩体`的取值为单独爆破作用下的较小值。因此,根据算例1中的取值,本算例中′=(30,35,1,40,45,75,30,35,1,40,45,75,55,65)。忽略地应力和模型顶部荷载的影响,将各岩体的线性模型、类非线性模型结果与数值模拟平均结果进行对比,对比结果如图10所示。
但既然决定要改,就要下决心、立规矩、出政策。为提升我国食品工业整体发展水平,中央与地方开始出台一系列支持政策,用以推动食品工业前行。
从图10可知,数值模拟中所列岩体的位移及速度响应均呈幅值逐步递减的规律,最后达到平衡状态。与线性模型相比,类非线性模型在动力响应极值上更接近数值模拟结果,且更快达到平衡状态,充分揭示了水平采空区群的动力响应规律。
为保证间隔间柱单段爆破作业的安全性,即防止顶板因振动作用力过大,导致岩体内的拉应力超过其极限抗拉强度,发生失稳破坏,需要对关键空区顶板的振动速度进行监测。为了确保监测人员及仪器的安全,禁止直接对爆破载荷作用的空区(空区1和空区3)进行监测。因此,选取空区2和空区4顶板作为监测对象,如图11所示。其中,监测点与爆破荷载1和2的距离约50 m,监测点与爆破荷载2的距离约41 m。
图12所示为监测点和的速度时程监测曲线。从图12可以看出,监测点和的最大速度小于0.06 m/s,均低于GB6722—2014“爆破安全规程”[15]中设定的地下爆破安全振动速度(0.18~0.30 m/s)。因此,间隔间柱单段爆破作业具有较高的安全性。

图9 5个单元空区组成的水平采空区群数值模型
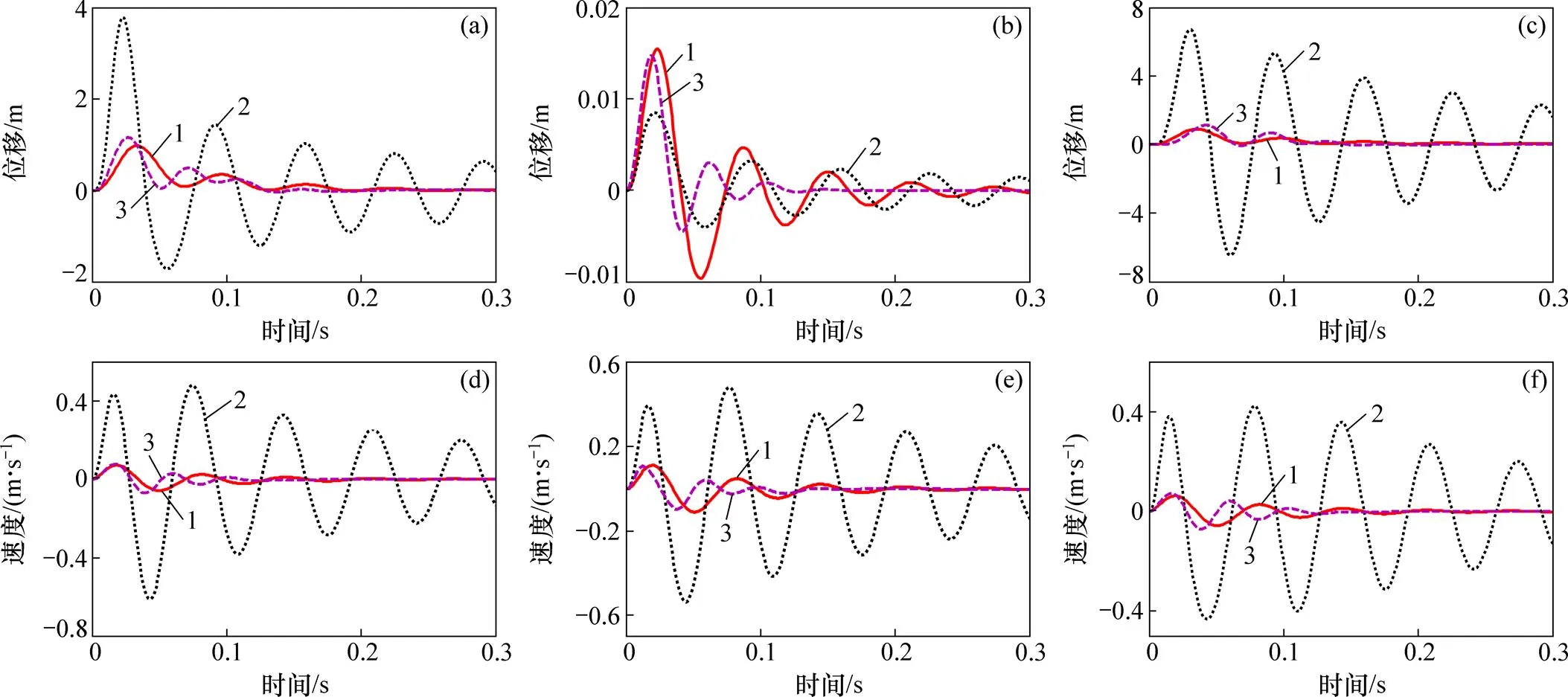
(a) 空区1顶板位移时程曲线;(b) 间柱1位移时程曲线;(c) 间柱2位移时程曲线;(d) 空区2底板速度时程曲线;(e) 空区3顶板速度时程曲线;(f) 空区4顶板速度时程曲线
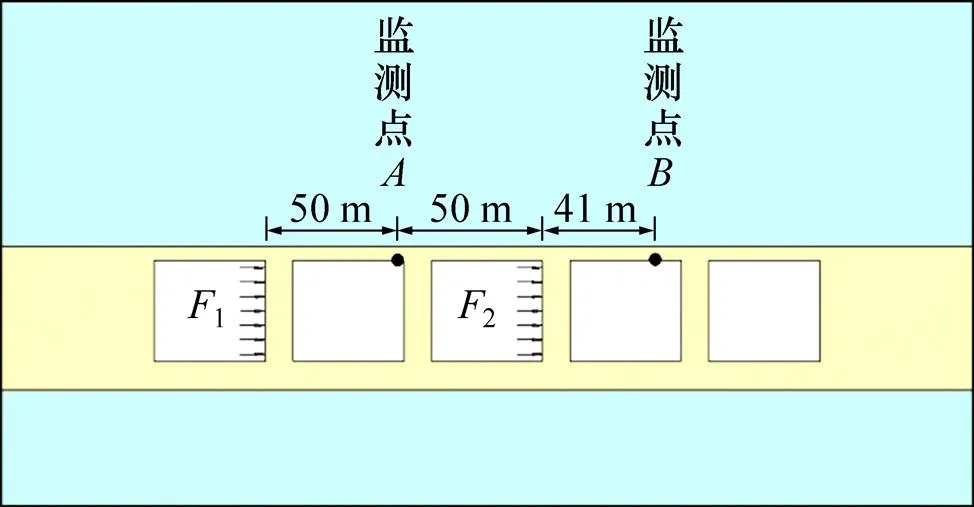
图11 监测点示意图
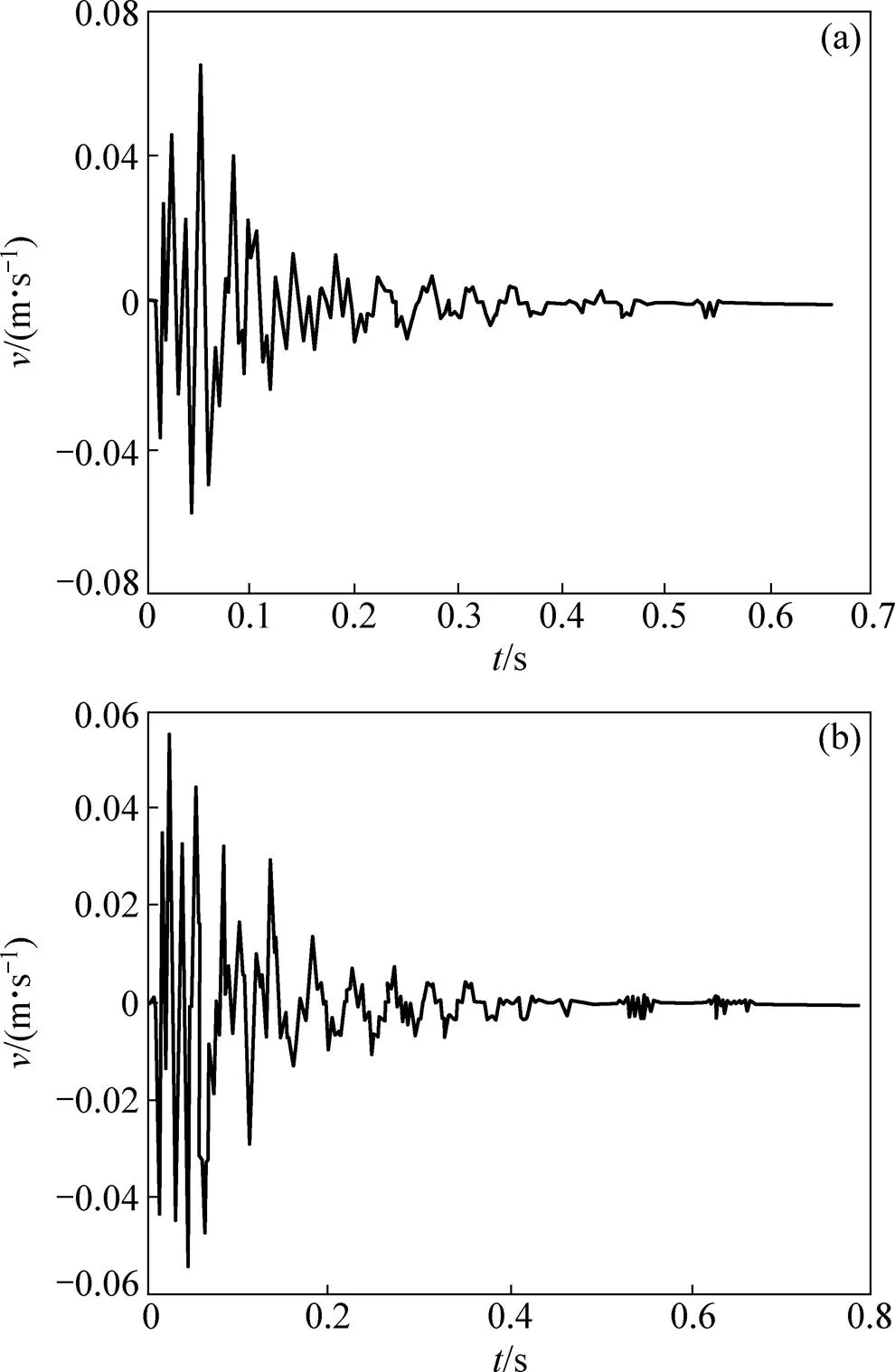
(a) 监测点A;(b) 监测点B
3 讨论
各空区顶(底)板及其围岩的能量损耗量与间柱未有明显的线性关系,这是因为岩体是非线性介质。在水平采空区群中,各岩体本身动力响应规律具有非线性振动的特性,相邻岩体之间的动力响应规律呈非线性变化。对的非线性取值,即为对线性振动模型的“类非线性”改进。
同一空区顶(底)板类非线性因子的取值接近,说明同一空区顶(底)板围岩所损耗的能量相近。
2个算例中,类非线性模型结果与数值模拟结果存在一定的时间差,主要原因是数值模拟中岩体内能量的传递具有时间效应,而类非线性模型中的能量传递是瞬间完成的。
在水平采空区群动力响应计算过程中,数值模拟耗时数小时,而类非线性振动模型仅耗时十几秒,极大地提高了求取空区群动力响应的效率。
目前类非线性多自由振动模型仅建立在线性系统的假设上,而采空区群属于非线性系统,构建空区群的非线性振动模型是将来研究的方向。
4 结论
1) 在线性多自由度振动模型的基础上,考虑到围岩对水平采空区群的水平地应力作用及能量耗散影响,引入水平地应力因子和类非线性因子,建立了适用于水平采空区群动力响应的类非线性多自由度振动模型。
2) 水平地应力对水平采空区群的动力响应无明显的影响,可忽略水平地应力因子的作用,即=0。
3) 采用标准动载荷()计算水平采空区群各岩体的类非线性因子是可行的。对于同一矿山,只需进行1次的计算,便可应用到类似工况,节省了的取值时间。
4) 单个间柱微差爆破及间隔间柱单段爆破2个算例结果表明,与线性模型对比,类非线性振动模型结果与数值模拟结果更加吻合,较好地揭示了水平采空区群各岩体的动力响应规律。
[1] 闫长斌, 徐国元. 竖向排列地下硐室群动力稳定性的数值模拟分析[J]. 中南大学学报(自然科学版), 2006, 37(3): 593−599. YAN Changbin, XU Guoyuan. Numerical simulation analysis on stability of vertically arranged underground chambers under dynamic load[J]. Journal of Central South University (Science and Technology), 2006, 37(3): 593−599.
[2] 隋斌, 朱维申, 李晓静. 地震荷载作用下大型地下洞室群的动态响应模拟[J]. 岩土工程学报, 2008, 30(12): 1877−1882. SUI Bin, ZHU Weishen, LI Xiaojing. Simulation on dynamic response of large underground opening complex under seismic loads[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(12): 1877−1882.
[3] 吕涛, 李海波, 杨建宏, 等. 溪洛渡地下洞室群地震响应的二维及三维数值模型比较分析研究[J]. 岩土力学, 2009, 30(3): 721−728. LÜ Tao, LI Haibo, YANG Jianhong, et al. Dynamic response analysis of underground cavern group based on 3D geologic model[J]. Rock and Soil Mechanics, 2009, 30(3): 721−728.
[4] 鲁文妍, 钟登华, 佟大威, 等. 基于三维地质模型的地下洞室群地震动力响应分析[J]. 岩土力学, 2012, 33(3): 919−924. LU Wenyan, ZHONG Denghua, TONG Dawei, et al. Dynamic response analysis of underground cavern group based on 3D geologic model[J]. Rock and Soil Mechanics, 2012, 33(3): 919−924.
[5] 盛谦, 崔臻, 刘加进, 等. 传递函数在地下工程地震响应研究中的应用[J]. 岩土力学, 2012, 33(8): 2253−2258. SHENG Qian, CUI Zhen, LIU Jiajin, et al. Application study of transfer function for seismic response analysis of underground engineering[J]. Rock and Soil Mechanics, 2012, 33(8): 2253−2258.
[6] 杨继华, 盛谦, 朱泽奇, 等. 地下岩体洞室群地震响应的加、卸载响应比分析[J]. 岩土力学, 2012, 33(7): 2127−2132. YANG Jihua, SHENG Qian, ZHU Zeqi, et al. Loading/unloading response ratio study of seismic response on underground rock cavern group[J]. Rock and Soil Mechanics, 2012, 33(7): 2127−2132.
[7] 崔臻, 盛谦, 刘加进, 等. 基于小波包的地下洞室群地震响应及其频谱特性研究[J]. 岩土力学, 2010, 31(12): 3901−3906. CUI Zhen, SHENG Qian, LIU Jiajin, et al. Spectrum characteristics analysis of seismic response for underground caverns via wavelet packet[J]. Rock and Soil Mechanics, 2012, 31(12): 3901−3906.
[8] 黄靓, 包堂堂, 施楚贤. 剪切型多自由度结构的层间初始侧移刚度实测方法[J]. 工程力学, 2013, 30(8): 90−95. HUANG Liang, BAO Tangtang, SHI Chuxian. Stiffness measurement method of shearing MDOF structure[J]. Engineering Mechanics, 2013, 30(8): 90−95.
[9] 李寿英, 陈政清, 顾明. 斜拉桥拉索风雨激振的两质量三自由度理论模型[J]. 土木工程学报, 2007, 40(10): 60−66. LI Shouying, CHEN Zhengqing, GU Ming. A theoretical model of rain-wind induced vibration of stay cables: a couple two-mass oscillators with three degree-of-freedoms[J]. China Civil Engineering Journal, 2007, 40(10): 60−66.
[10] 肖建清, 冯夏庭, 丁德馨, 等. 常幅循环荷载作用下岩石的滞后及阻尼效应研究[J]. 岩石力学与工程学报, 2010, 29(8): 1677−1683. XIAO Jianqing, FENG Xiating, DING Dexin, et al. Study of hysteresis and damping effects of rock subjected to constant amplitude cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1677−1683.
[11] 刘建锋, 谢和平, 徐进, 等. 循环荷载下岩石变形参数和阻尼参数探讨[J]. 岩石力学与工程学报, 2012, 31(4): 770−777. LIU Jianfeng, XIE Heping, XU Jin, et al. Discussion on deformation and damping parameters of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 770−777.
[12] 丁海平, 马俊玲. 基于场地特征周期的瑞利阻尼确定方法[J]. 岩土力学, 2013, 34(增刊2): 35−40. DING Haiping, MA Junling. A method for determining Rayleigh damping based on site characteristic period[J]. Rock and Soil Mechanics, 2013, 34(Supp. 2): 35−40.
[13] 姜立春, 魏叙深. 采动应力作用下陡倾板裂状岩体巷道溃屈破坏[J]. 辽宁工程技术大学学报(自然科学版), 2015, 34(1): 15−20. JIANG Lichun, WEI Xushen. Buckling failure of roadway in vertically stratified rock under mining stress[J]. Journal of Liaoning Technical University: Natural Science, 2015, 34(1): 15−20.
[14] 蔚立元, 李术才, 徐帮树. 青岛小净距海底隧道爆破振动响应研究[J]. 土木工程学报, 2010, 43(8): 100−108. YU Liyuan, LI Shucai, XU Bangshu. Study on the effect of blasting vibration for Qingdao twin subsea tunnels[J]. China Civil Engineering Journal, 2010, 43(8): 100−108.
[15] GB 6722—2014. 安全爆破规程[S]. GB 6722—2014. Safety regulations of blasting[S].
(编辑 赵俊)
A similar nonlinear vibration model for dynamic response of horizontal goaf group
JIANG Lichun1, 2, ZENG Junjia2, WU Aixiang3
(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;2. Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640, China;3. School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China)
On the basis of linear multi-degree of freedom (MDOF) vibration model, considering the effect of horizontal geostatic stress and energy dissipation caused by surrounding rocks, a similar nonlinear vibration model for horizontal goaf group was established by introducing horizontal geostatic stress factorand similar nonlinear factor. Similar nonlinear vibration model was investigated and verified based on two cases of millisecond blasting in single barrier pillar and single deck blasting in interval barrier pillars. The results show that the dynamic response results are not obviously affected by horizontal geostatic stress, and the effect of horizontal geostatic stress could be ignored (=0). It is feasible to use the standard dynamic load() to calculate the similar nonlinear factorof each rock mass in horizontal goaf group, andcould be applied to similar conditions by calculating only once for the same mine, which saves the selecting time of; compared with linear model, similar nonlinear vibration model result is more consistent with numerical simulation result, which effectively reveals the dynamic response law of horizontal goaf group.
rock mass mechanics; horizontal goaf group; dynamic response; MDOF vibration model; horizontal geostatic stress; energy dissipation
10.11817/j.issn.1672−7207.2017.06.022
TU 45
A
1672−7207(2017)06−1577−08
2016−06−06;
2016−08−25
国家“十二五”科技支撑计划项目(2012BAB08B02);国家自然科学基金资助项目(51174093, 51374035) (Project (2012BAB08B02) supported by the National Science and Technology Pillar Program during the 12th “Five-Year” Plan Period of China; Projects(51174093, 51374035) supported by the National Natural Science Foundation of China)
吴爱祥,教授,博士生导师,从事金属矿安全开采技术研究;E-mail:wuaixiang@126.com
