岩体结构面对爆炸冲击工程响应的影响
2017-07-21胡建华高宏伟薛小蒙周科平
胡建华,高宏伟,薛小蒙, 2,周科平
岩体结构面对爆炸冲击工程响应的影响
胡建华1,高宏伟1,薛小蒙1, 2,周科平1
(1. 中南大学资源与安全工程学院,湖南省深部金属矿开发与灾害控制重点实验室,湖南长沙,410083;2. 中钢集团马鞍山矿山研究院有限公司, 安徽马鞍山,243000)
基于裂隙岩体的结构面是矿山安全生产的重要影响因素,对爆炸冲击应力波的传播规律有重要影响,以铜坑矿岩体力学参数为基础,采用ANSYS /LS-DYNA软件,建立结构面厚度、倾角及结构面充填材料对爆炸冲击工程响应的数值模型,获取结构面对爆炸冲击下的工程响应特性,并基于神经网络构建结构面参数灰关联神经网络预测模型,确定结构面参数在爆破冲击工程响应的重要度。研究结果表明:结构面前、后测点的质点峰值振速的衰减度与结构面厚度呈指数函数,当结构面厚度为0,5,10,15和20 cm时,衰减度分别为0.365,1.508,2.303,2.418和2.443;结构面倾角对爆破冲击工程响应与衰减度呈正相关,当结构面倾角为30°,45°和60°时,衰减度分别为1.580,2.495和2.698;当结构面的充填材料为胶结、碎屑、泥质时,质点峰值振速的衰减度分别为2.303,2.458和2.598,与充填材料的强度呈负相关;3种因素的影响度由大到小依次为结构面厚度、倾角、充填材料强度。
结构面;爆炸冲击;质点峰值振速;影响度
岩体是由完整岩石和结构面构成的地质体,其结构面对岩体力学性质和爆破工程响应有重要的影响。在矿山破岩、开挖等爆破工程中,当岩体中存在结构面时,爆破应力波会在结构面处产生反射、透射现象,阻碍应力波的传播,加速能量衰减。Mckenzie 等[1]指出,应力波的衰减取决于裂隙的数量、宽度以及充填物的波阻抗;柯新华等[2]认为不同尺度结构面对应力波衰减应采用不同方法研究其工程响应特性,并提出了采用应力波时空衰减相结合的方法研究多结构面耦合作用对应力波衰减的影响规律;张秀丽等[3]通过数值研究方法发现节理面能阻碍波的传播、加速波的衰减,并指出节理面越多,波的反射越强,透射越弱;王洋等[4]采用LS-DYNA与离散元3DEC相结合的方法,分别模拟了爆炸应力波在不同裂隙条件中传播的特点,认为岩体中裂隙越多,最小主应力降低越快;周剑等[5−6]根据应力波的时延理论推导了应力波透射线弹性结构面的时延关系式,并运用数值软件模拟了应力波穿越不同产状大型结构面的传播特征;胡世丽等[7]在研究结构面间距对透射波的影响时发现,结构面间距与波长之比存在1个临界值,超过此临界值时,多重反射和投射对应力波传播影响很小,对透射系数几乎没有影响。此外,已有大量研究表明爆炸冲击波的能量随着传播距离的增加而衰减,并在爆破中远区衰减为应力波。彭府华等[8]采用全数字型多通道微震检测系统,结合现场试验拟合得出应力波传播速度,获得振幅与传播距离的衰减特性曲线;李洪涛等[9]基于地震学相关理论,研究了爆破地震的能量随距离衰减规律,证明了爆破地震的能量随距离迅速衰减。为探求结构面参数在爆炸冲击应力波随距离传播工程响应的影响及其程度,本文作者采用ANSYS数值模拟软件,以铜坑矿为例,建立不同状态下结构面的有限元模型,分析结构面厚度、角度以及充填物材料性质对爆破冲击应力波传播的影响,并通过神经网络软件Easy NN-plus对各因素的影响度进行评价。
1 岩体结构面影响因素
1.1 工程概况
铜坑矿属于锡多金属矿山,岩体节理裂隙较发育,不同类型结构面的存在导致岩体力学参数降低。在钻爆开采过程中,由于存在断面过大、爆破震动和结构面分布等不良因素,导致采矿过程中采动爆破能耗损失大,工程结构出现局部冒顶、片帮甚至垮塌等灾变现象,给矿山生产效率和安全带来极大危害。为设计合理的爆破参数,分析不同状态下结构面对爆炸冲击应力波传播的影响十分重要。
根据矿山提供的地质资料,其岩体与结构面的力学参数见表1。
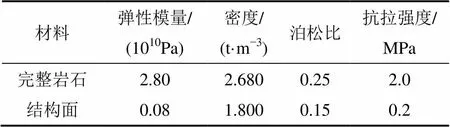
表1 岩石及结构面物理力学参数
1.2 结构面影响因素
由于岩体中结构面规模、产状各异,在构建模型时,将岩体中的优势结构面及附近的较小裂隙一致等效为有一定厚度的结构面。Hakan等[10]认为岩体中应力波传播至结构面处产生的反射、透射现象与结构面的厚度、角度有关。由于岩体结构面充填物是重要参数,在模型分析中,主要考察结构面厚度、角度及结构面充填物对爆炸冲击应力波传播的影响。
1.3 爆炸荷载加载方法
对于矿山地下工程,研究的工程响应主要针对爆炸作用的中远区,针对该区域,许红涛等[11−12]提出了爆炸等效荷载施加模拟爆炸方法,并实现爆破冲击工程效应的模拟方法。根据圣维南原理,在爆源处采用三角形曲线加载方式施加爆炸荷载。加载力随时间的变化规律如图1所示。

图1 爆炸三角形曲线加载
1.4 数值模型
为简化计算,采用线弹性材料模型,并将其简化为长度×宽度×厚度为6.00 m×4.00 m×0.05 m的长方体,沿宽度方向布置贯穿模型的裂隙结构面,模型采用共节点算法,映射网格划分形式,网格长度为0.05 m,四周采用无反射边界,并对前、后2个面进行法线方向上的位移约束。截取部分模型见图2,材料力学参数见表1。以爆源中心为起点,沿长度方向在模型中布置测线,施加三角形爆炸荷载曲线。为考察爆炸冲击波在结构面前后传播过程中的质点振速变化的对比情况,选取的测点充分涵盖了结构面前、后质点。为了更清晰地观察质点振速的变化,测点距爆源中心的距离不应设过大,分别设为0.1,0.7,1.1,1.5和1.9 m,其中0.1 m和0.7 m处的测点位于结构面与爆源之间,其余测点均位于结构面之后的测线上。
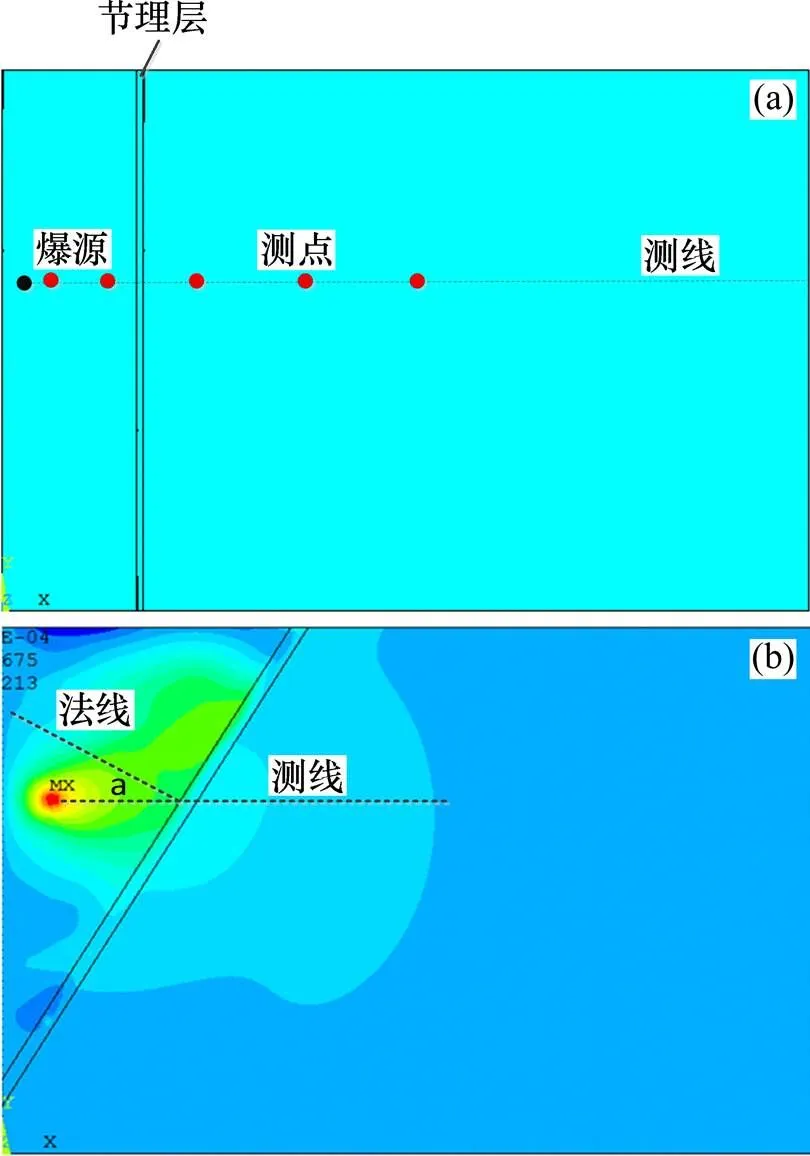
(a) 测点布置图;(b) 结构模型图
为研究结构面的厚度、倾角和填充物对爆炸冲击应力波传播的影响,采用建立的模型分别对3种因素进行分析。设置结构面参数时考虑到后续计算时参与计算的结构面前后测点的距离仅为0.4 m,故模型中的节理层厚度不应设过大,将其分别设置为0,5,10,15和20 cm共5种,结构面倾角可设为0°,30°,45°和60°共4种,并依据强度不同选用胶结充填、碎屑充填和泥质填充3种充填材料类型共10种组合分析模式,模型组合方式的计算参数见表2,分别观察爆炸冲击经过各测点时相应质点的振动速度,比较不同参数组合下的工程响应(质点振速衰减)规律。充填物材料参数见表3。
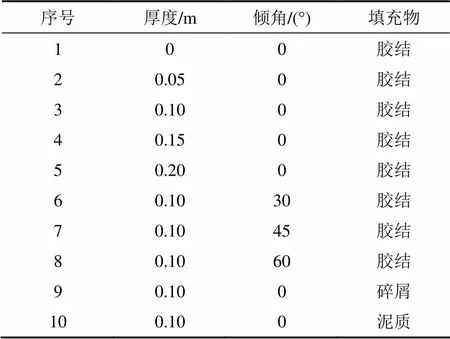
表2 计算参数组合表
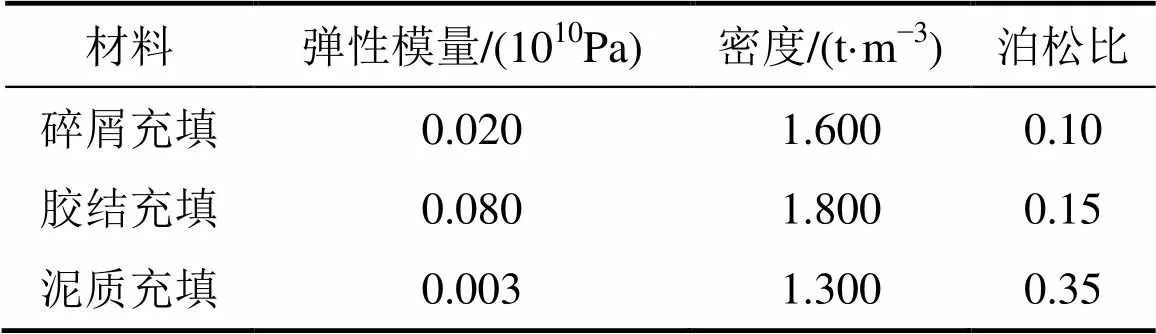
表3 结构面充填物材料参数
2 数值结果与分析
2.1 结构面厚度分析
在相同的结构面倾角及充填强度下,不同厚度爆破冲击应力波的传播各测点的向速度−时间曲线见图3。
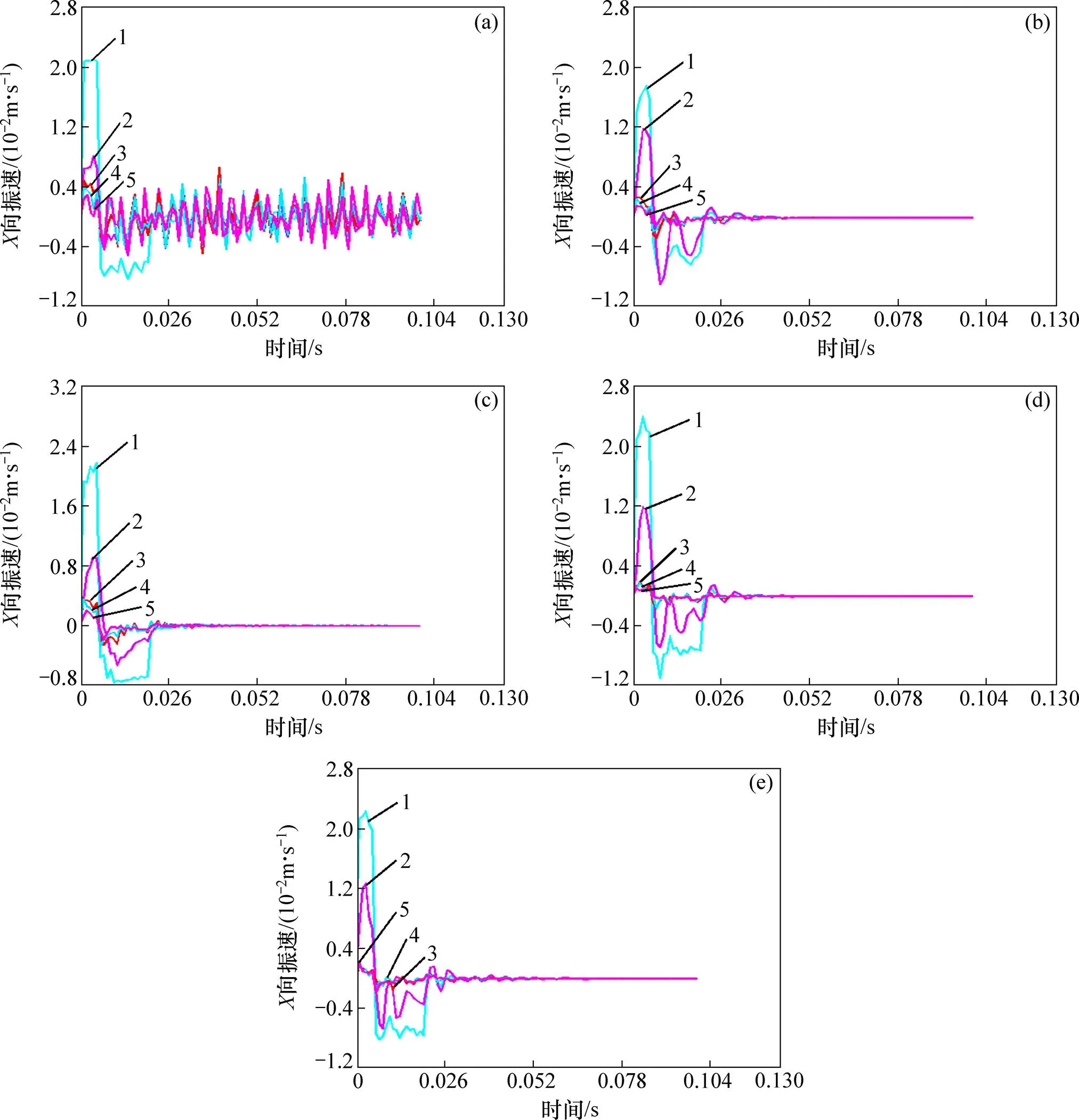
结构面厚度/cm:(a) 0(无节理);(b) 5;(c) 10;(d) 15;(e) 20
由图3可知:随着与爆源距离增大,爆破振动在岩体传播中均发生衰减;结构面的厚度是影响矿山工程爆破振动传播的重要控制因素;在测点距离爆源0.1 m和0.7 m处,由于测点位于爆源与结构面之间,测点振动速度幅值基本相同,主要来源于爆破应力波传播至结构面处质点响应速度以及结构面反射产生的应力波。另3个测点位于结构面的后方,在无结构面条件下,主要表现出岩体对爆炸波的正常衰减,而在有结构面条件下,向振速差异较大,且随着结构面厚度增加,衰减幅度增加,表明结构面在一定程度上吸收了爆炸应力波的能量,进一步增强了爆炸波的衰减。各测点的和向速度见表4。由表4可以看出:各测点的向振速远小于其向振速,遭遇结构面时,向振速衰减规律不太明显,衰减程度远比向的小。这说明此类型结构面主要导致向质点振速衰减。此外,对比相同厚度条件下各测点振速可以看出:随着传播距离增大,振速的衰减均趋向于缓慢,甚至出现波动。

表4 不同节理厚度下质点速度峰值
表4中5种节理厚度条件下各测点的质点振动速度峰值曲线见图4(将结构面厚度0 cm的曲线设为基准线,以方便对比)。
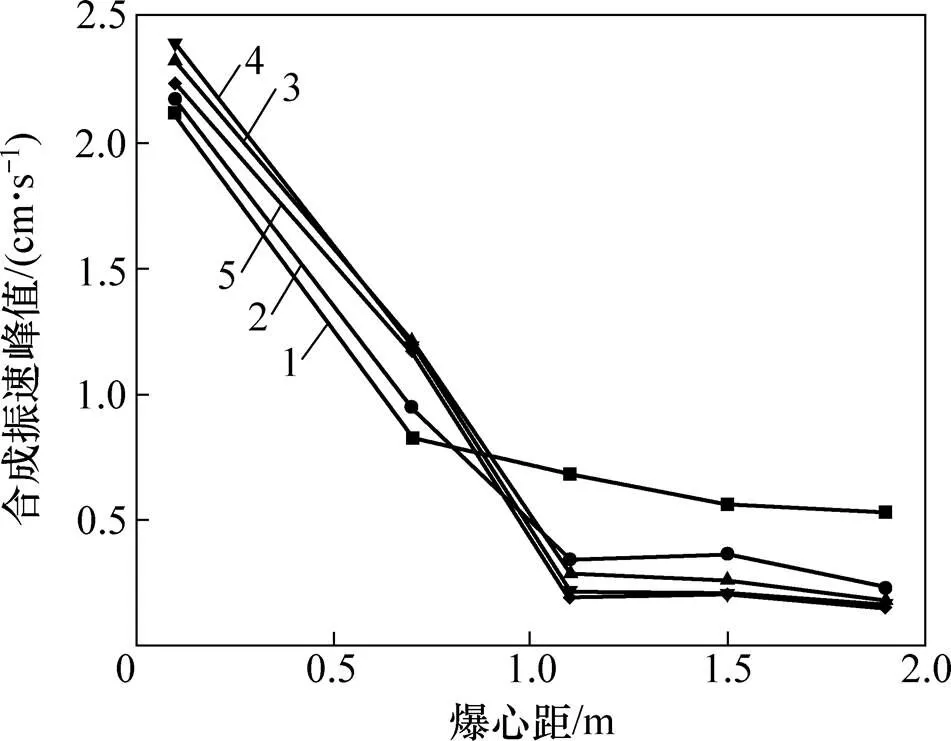
节理厚度/cm:1—0(基准线);2—5;3—10;4—15;5—20。
李洪涛等[9]的研究表明:爆炸振动波总能量与振速的平方近似成正比关系,即波速越大,应力波能量也越大。由图4可知:爆破冲击应力波穿过结构面后,振速大幅度下降,且结构面后的各测点峰值振速均小于无结构面时相同质点的振速,说明结构面吸收了爆破冲击应力波的部分能量。定义衰减度为单位长度质点振速的衰减值,主要用于表征质点振动衰减随着结构面的特征参数变化的程度,可根据式(1)计算。计算应力波通过不同结构面厚度的前后测点的振速峰值的衰减度和间距,绘制并拟合结构面厚度−衰减度曲线,如图5所示。

式中:1和0为待测2点的速度,即爆心距1.1 m和0.7 m处的质点振速峰值,cm/s;为2个测点之间的距离,m,此处取测点2和测点3为计算目标,其值为0.4 m。
由图5可知:5种结构面厚度对应的衰减度分别为0.365,1.508,2.303,2.418和2.443。可以得知:当结构面厚度在一定的范围内时,随着结构面厚度越大,应力波通过时质点振速衰减越快;当结构面厚度超过某一数值时(如超过15 cm时),衰减度慢慢趋于稳定。这说明当结构面厚度与结构面前、后两测点间距的比例达到某一值后,衰减度将不再继续增大,与实际情况基本相符。其拟合方程式为

式中:为结构面厚度(m)。
图5 结构面厚度−衰减度拟合曲线
Fig. 5 Fitting curve of thickness of structural planes−attenuation degree
2.2 结构面倾角分析
结构面的倾角主要影响爆破应力波的传播方向的衰减,并通过不同倾角下的水平厚度变化改变爆破应力波衰减度。同时,在结构面的反射响应下,结构面前方的测点振动速度增加,形成爆破冲击应力波与反射波的叠加。在同一结构面厚度、不同倾角条件下,爆破冲击应力波在结构面岩体中各测点的质点振速峰值如表5所示。

表5 不同结构面倾角质点速度峰值
不同倾角条件下质点振速峰值变化见图6。由图6可知:结构面的角度也是影响矿山工程爆破振动传播的重要控制因素;当结构面厚度一致、爆炸荷载相同时,爆炸应力波通过不同倾角结构面时质点振速峰值的衰减速率均比其他段的大。根据计算,当结构面倾角为0°,30°,45°和60°时,衰减度分别为2.303,1.580,2.495和2.698。结构面倾角越大,衰减度也越大。这是因为结构面倾角越大,爆炸冲击应力波传播时遭受反射和绕射的影响越大,而且因倾角增大造成的结构面水平厚度也越大,因此,爆炸应力波在结构面内传播的能量损耗也随之增大;当倾角为0°时,应力波垂直结构面入射,不少能量沿原路反射,导致结构面偏爆源一侧产生能量聚集效应,测点振速偏大,衰减度计算值偏大。
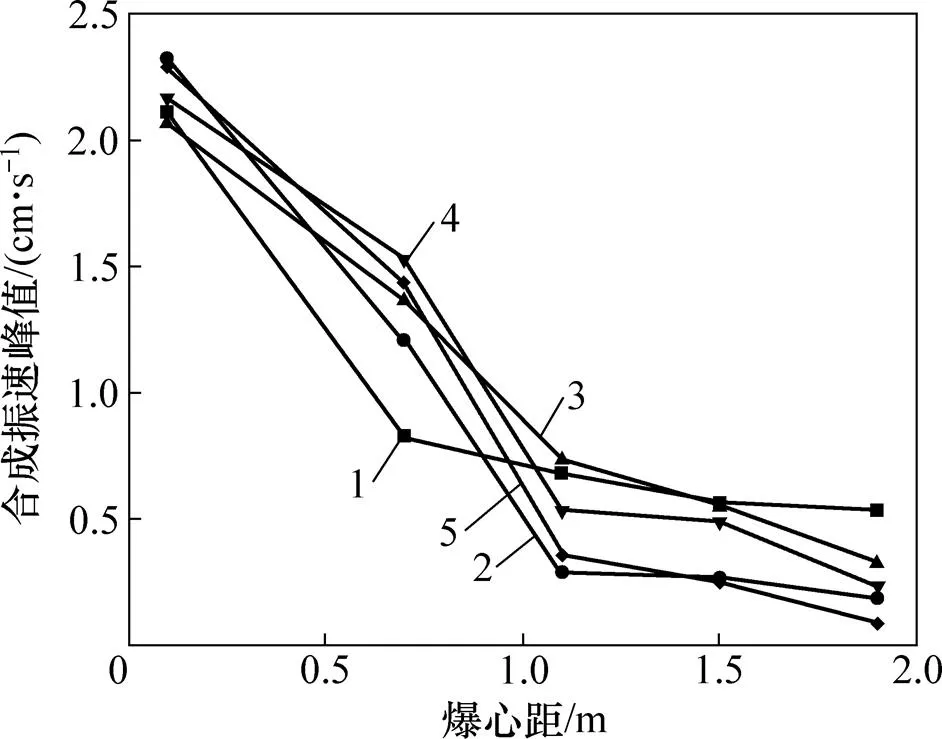
结构面倾角/(°):1—无结构面;2—0;3—30;4—45;5—60。
2.3 结构面充填材料分析
在相同的结构面厚度及倾角条件下,不同充填物爆破冲击应力波在结构面岩体中各测点的质点振速峰值见表6。
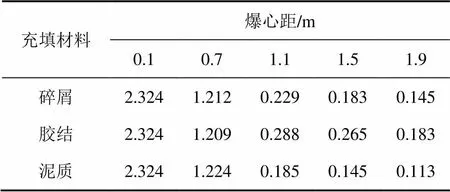
表6 不同充填材料下测点振速峰值
不同充填物条件下质点振速峰值变化见图7。由图7可知:结构面充填物的存在加快了质点振速峰值的衰减,同时受结构面的影响,爆破冲击应力波与反射波叠加,在爆破源与结构面间形成振动速度增加的趋势。爆破冲击应力波通过3种不同充填物的结构面时质点振速峰值的衰减速率均比其他段的大,根据计算,衰减度分别为2.458,2.303和2.598。胶结充填材料强度大,完整性好,结构面与两侧岩石力学性质相差不大,损耗的爆炸冲击能量较少,因此,质点振速的衰减度最小;碎屑充填材料强度较小,完整性较差,应力波在结构面充填物中的反射、折射较多,损耗能量较多,质点振速的衰减度较大;泥质充填材料强度最小,细微颗粒多,含水多,结构面与两侧岩石力学性质相差较大,故损耗能量最多,质点振速衰减度最大。

1—无结构面;2—碎屑;3—胶结;4—泥质。
3 影响因素的相对重要性评价
灰关联分析作为灰色系统的分析方法之一,可通过计算分析影响某现象发生的各因素亲疏关系,该方法在矿业领域可用于建立安全评价体系[13]。而神经网络模型可用于大规模并行分布处理非线性信息处理系统,通过学习和存储大量的输入层−输出层映射关系并进行推理,找出对应关系,如空区地基稳定性、爆炸冲击预测及影响因素的敏感性预测等[14−16]。胡建华等[17]耦合了灰关联分析和神经网络方法,建立了空区危险度的结构尺寸效应灰关联神经网络模型,分析了空区危险度与结构尺寸参数间的影响程度及响应 关系。
为深入分析结构面厚度、倾角及充填材料对爆炸冲击传播规律的影响程度,运用式(3)对结构面厚度、倾角进行归一化处理,并根据岩体质量分级中节理面因素对3种充填材料进行评价,得出节理层强度且进行归一化处理。将3种影响因素作为输入层因子,衰减度处理后化为关联度用作模型的学习输出因子,基于神经网络软件Easy NN-plus建立结构面参数灰关联神经网络预测模型,见图8。
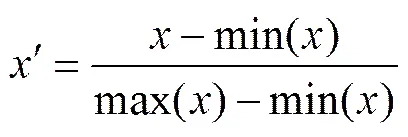
式中:′为影响因素归一化值;为影响因素的评价指标值;min()和max()分别为影响因素评价指标最小和最大值。
图8 神经网络预测模型
Fig. 8 Neural network prediction model
将学习率、惯性系数和目标训练误差分别设为0.60,0.80和0.01[18],得到表征3个输入因子对输出因子的影响度的训练结果,见图9。
由图9可知:学习率、惯性系数和目标训练误差在一定条件下,对结构面厚度、倾角和充填料强度这3种因素对输出结果的影响度分别为69.8%,16.2%和14.0%,即影响度由大到小依次为结构面厚度、倾角、充填材料强度,说明这3个因素中,结构面厚度对爆炸冲击应力波传播的质点振速峰值衰减贡献最大,结构面充填材料强度贡献最小。
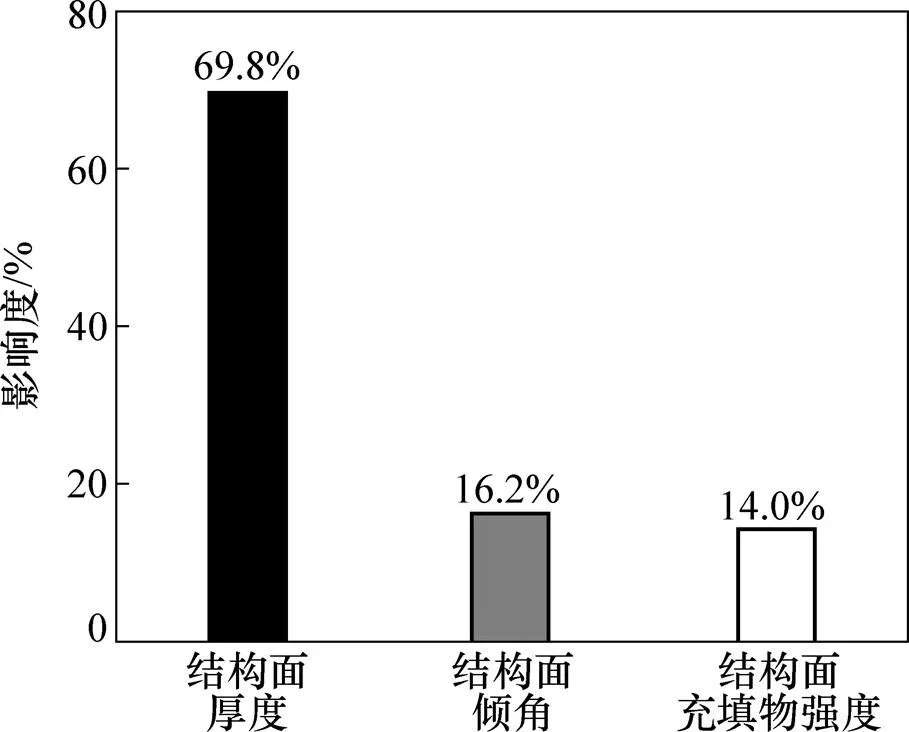
图9 影响因素的影响度
4 结论
1) 爆炸冲击应力波通过结构面时能量会被其吸收且主要产生质点向振速衰减,衰减度与结构面厚度呈指数函数规律,当结构面厚度为0,5,10,15和20 cm时,衰减度分别为0.365,1.508,2.303,2.418和2.443。
2) 爆炸冲击穿过结构面时,结构面倾角与质点振速的衰减度呈正相关性。当倾角为0°,30°,45°和60°时,衰减度分别为2.303,1.580,2.495和2.698。当结构面倾角为0°时,应力波垂直结构面入射,不少能量沿原路反射,导致结构面偏爆源一侧产生能量聚集效应,测点振速偏大,衰减度计算值偏大。
3) 当结构面充填材料分别取胶结充填、碎屑充填、泥质充填时,爆炸冲击应力波传播时质点振速衰减度分别为2.303,2.458和2.598,与充填材料的强度呈负相关。
4) 基于神经网络构建结构面参数灰关联神经网络预测模型,研究结构面各因素的影响度,影响度由大到小依次为结构面厚度、倾角、充填材料强度。
[1] Mckenzie C K, Stacey G P, Gladwin M T. Sonic wave characteristics of rock mass[J]. International Journal of Rock Mechanics and Mining Science, 1982, 19(1): 25−30.
[2] 柯新华, 王观石, 金解放, 等. 结构面尺度对应力波衰减影响的研究进展[J]. 铜业工程, 2011(6): 7−11. KE Xinhua, WANG Guangshi, JIN Jiefang, et al. Research progress of influence of interfaces dimension to stress wave attenuation[J]. Copper Engineering, 2011(6): 7−11.
[3] 张秀丽, 焦玉勇, 刘泉声, 等. 节理对爆炸波传播影响的数值研究[J]. 岩土力学, 2008, 29(3): 717−721. ZHANG Xiuli, JIAO Yuyong, LIU Qiansheng, et al. Numerical study on effect of joints on blasting wave propagation in rock mass[J]. Rock and Soil Mechanics, 2008, 29(3): 717−721.
[4] 王洋, 叶海旺, 李延真. 裂隙岩体爆破数值模拟研究[J]. 爆破, 2012, 29(3): 20−22. WANG Yang, YE Haiwang, LI Yanzhen. Numerical simulation on jointed and fractured rock blasting[J]. Blasting, 2012, 29(3): 20−22.
[5] 周剑, 张路青. 应力波时延与结构面刚度的关联性分析[J]. 岩石力学与工程学报, 2013, 32(2): 3266−3274. ZHOU Jian, ZHANG Luqing. Study of relevancy between stress wave time delays and stiffness of structural surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 3266−3274.
[6] 周剑, 张路青, 胡瑞林, 等. 大型结构面产状影响下应力波传播规律研究[J]. 岩石力学与工程学报, 2011, 30(4): 769−780. ZHOU Jian, ZHANG Luqing, HU Ruilin, et al. Study of rules of stress waves propagation under various attitudes of large-scale fractures[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 769−780.
[7] 胡世丽, 罗嗣海, 王观石. 结构面间距对透射波的影响[J]. 矿冶工程, 2011, 31(4): 5−8. HU Shili, LUO Sihai, WANG Guanshi. Influence of structural face interval on transmission wave[J]. Mining and Metallurgical Engineering, 2011, 31(4): 5−8.
[8] 彭府华, 李庶林, 程建勇, 等. 中尺度复杂岩体应力波传播特性的微震试验研究[J]. 岩土工程学报, 2014, 36(2): 312−319. PENG Fuhua, LI Shulin, CHENG Jianyong, et al. Experimental study on characteristics of stress wave propagation in mesoscale and complex rock mass by microseismic monitoring[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 312−319.
[9] 李洪涛, 卢文波, 舒大强, 等. 爆破地震波的能量衰减规律研究[J]. 岩石力学与工程学报, 2010, 29(1): 3364−3369. LI Hongtao, LU Wenbo, SHU Daqiang, et al. Study of energy attenuation law of blast-induced seismic wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 3364−3369.
[10] Hakan A K, Konuk A. The effect of discontinuity frequency on ground vibration from bench blasting: a case study[J]. Soil Dynamics and Earthquake Engineering, 2008, 28(9): 686−694.
[11] 许红涛, 卢文波, 周小恒. 爆破震动场动力有限元模拟中爆破荷载的等效施加方法[J]. 武汉大学学报(工学版), 2008, 41(1): 67−71. XU Hongtao, LU Wenbo, ZHOU Xiaoheng. An equivalent approach for acting blasting load in dynamic finite element simulation of blasting vibration[J]. Engineering Journal of Wuhan University, 2008, 41(1): 67−71.
[12] 张玉成, 杨光华, 刘鹏, 等. 爆破何在在数值计算中的等效施加方法[J]. 地下空间与工程学报, 2012, 8(1): 56−64. ZHANG Yucheng, YANG Guanghua, LIU Peng, et al. An equivalent approach for acting blasting load in dynamic numerical simulation of blasting vibration[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(1): 56−64.
[13] 曹树刚, 徐阿猛, 刘延保, 等. 基于灰色关联分析的煤矿安全综合评价[J]. 采矿与安全工程学报, 2007, 24(2): 141−145. CAO Shugang, XU Ameng, LIU Yanbao, et al. Comprehensive assessment of security in coal mines based on grey relevance analysis[J]. Journal of Mining & Safety Engineering, 2007, 24(2): 141−145.
[14] 丁陈建, 汪吉林. 神经网络法的采空区地基稳定性评价[J]. 采矿与安全工程学报, 2009, 26(2): 208−211. DING Chenjian, WANG Jilin. Using artificial neural network to assess the stability of goaf foundation[J]. Journal of Mining & Safety Engineering, 2009, 26(2): 208−211.
[15] 袁俊明, 刘玉存, 王建华, 等. 基于粒子群神经网络的黑索今基混合炸药大隔板试验冲击波感度预测[J]. 兵工学报, 2014, 35(2): 188−193. YUAN Junming, LIU Yucun, WANG Jianhua, et al. Prediction of shock sensitivity of RDX-based composite explosive by particle swarm neural network in large-scale gap test[J]. Acta Armamentarii, 2014, 35(2): 188−193.
[16] WANG Rui, JIANG Juncheng, PAN Yong. Prediction of impact sensitivity of nonheterocyclic nitroenergetic compounds using genetic algorithm and artificial neural network[J]. Journal of Energetic Materials, 2012, 30(2): 135−155.
[17] 胡建华, 甯瑜琳, 张行成, 等. 群空区危险度的结构尺寸效应灰关联神经网络模型[J]. 中南大学学报(自然科学版), 2012, 43(10): 3982−3988. HU Jianhua, NING Yulin, ZHANG Xingcheng, et al. Risk factor forecast based on neural network and grey relational analysis on physical dimension effect of mine goafs[J]. Journal of Central South University (Science and Technology), 2012, 43(10): 3982−3988.
[18] 蒋复量, 周科平, 李书娜, 等. 基于粗糙集−神经网络的矿山地质环境影响评价模型及应用[J]. 中国安全科学学报, 2009, 19(8): 126−132. JIANG Fuliang, ZHOU Keping, LI Shuna, et al. Study on the model of mines’ geological environmental impact assessment based on rough set and artificial neural network and its application[J]. China Safety Science Journal, 2009, 19(8): 126−132.
(编辑 陈灿华)
Influence of structural planes on response of explosion shock engineering
HU Jianhua1, GAO Hongwei1, XUE Xiaomeng1, 2, ZHOU Keping1
(1. Hunan Key Laboratory of Resource Exploitation and Hazard Control for Deep Metal Mines,School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. Sinosteel Maanshan Institute of Mining Research Co. Ltd., Maanshan 243000, China)
Considering that structural plane of fractured rock mass is one of the important factors that affects mine safety production, and it has important effect on the propagation law of explosion shock waves, blasting engineering response numerical models with different structural planes’ thicknesses, angles and structural planes’ filling material conditions were established based on rock mass mechanics parameters and ANSYS/LS-DYNA software, structural plane engineering’s response characteristics were obtained. Then neural network forecasting model based on grey relational analysis with different structural plane parameters was built by neural network to study the response degree of structural plane parameters in blasting engineering. The results show that attenuation degree before and after the structure’s peak particle vibration velocities presents exponential function with structural plane’s thickness. When the thickness is 0, 5, 10, 15 and 20 cm, attenuation degree is 0.365, 1.508, 2.303, 2.418 and 2.443, respectively. Attenuation degree is alsopositively correlated with structural plane’s angle, when the angle is 30°, 45° and 60°, the attenuation degree is 1.580, 2.495 and 2.698, respectively. When structural plane’s filling material is consolidated, debris, argillaceous and attenuation degree is 2.303, 2.458 and 2.598, respectively, and it is negatively related to intensity of filling material. The influencing degree of three factors from big to small is structural plane’s thickness, angle and intensity of filling material.
structural planes; explosion shock; peak particle vibration velocities; influencing degree
10.11817/j.issn.1672−7207.2017.06.020
O383
A
1672−7207(2017)06−1560−08
2016−07−10;
2016−08−22
国家“十二五”科技支撑计划项目(2015BAB12B01,2013BAB02B05);国家自然科学基金资助项目(41672298)(Projects (2015BAB12B01, 2013BAB02B05) supported by the National Science and Technology Pillar Program during the 12th “Five-year” Plan Period; Project (41672298) supported by the National Natural Science Foundation of China)
胡建华,博士,教授,从事高效安全采矿技术与岩土工程的稳定性分析研究;E-mail:hujh21@126.com
