多喷嘴撞击流混合器径向流场数值模拟研究
2017-07-19张建伟刘思源张学良王诺成
张建伟, 刘思源, 冯 颖, 张学良, 王诺成
(沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142)
多喷嘴撞击流混合器径向流场数值模拟研究
张建伟, 刘思源, 冯 颖, 张学良, 王诺成
(沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142)
为优化撞击流混合器结构,采用Fluent软件,对不同初始速度下的水平三向撞击流混合器径向流场特性进行数值模拟研究,并与两喷嘴对置式混合器进行对比.研究表明:水平三向撞击流混合器径向速度呈双峰分布,峰值点关于撞击点对称,随着初始速度的增大,峰值点位置不发生改变;三喷嘴混合器径向湍动能和湍流耗散率均呈单峰分布,峰值点即为撞击点;在相同初始速度下,三喷嘴混合器湍动能和湍流耗散率最大值分别为两喷嘴混合器湍动能和湍流耗散率最大值的2.21和2.06倍;4种初始速度下,水平三向撞击流混合器撞击点附近15 mm范围内的湍动能值均大于两喷嘴混合器的湍动能最大值.
撞击流混合器; 数值模拟; 径向速度; 湍动能; 湍流耗散率
撞击流作为一种科学概念,首先由Elperin提出[1].其基本原理是:通过流体的相向高速撞击,在撞击区产生高度湍动,极大地改善混合性能,以达到强化传热、传质等目的[2].我国学者伍沅、肖扬、周玉新等[3-4]从20世纪90年代开始了对撞击流的研究,研究结果表明:两股相向撞击的流体间发生强烈的相互作用和动量传递,产生强烈的微观混合效果.Siddiqui等[5-6]的研究表明:高流量下的撞击流反应器类似于平推流反应器,其内部的湍流动能耗散率远高于传统搅拌槽.孙怀宇等[7]等通过实验对撞击流反应器内流体的压力场进行测量,结果表明:围绕撞击区有一个强烈湍动的区域,能够促进混合及反应的进行.杨侠等[8]对不同导流筒间距下的立式循环撞击流反应器(简称VCISR)进行数值模拟,结果表明:导流筒间距为60 mm时反应器内时域压力波动强度达到最大值,速度分布梯度更大,微观混合效果更好.前人的研究多针对两喷嘴撞击流混合器,关于水平三向撞击流混合器的报道较少,考虑到混合器的湍动能及湍流耗散率在促进混合作用中起到的重要作用,及以往人们对水平三向撞击流混合器中的湍动能和湍流耗散率的研究还不够全面,本文对不同初始速度下的水平三向撞击流混合器的径向截面速度、湍动能和湍流耗散率进行数值模拟研究,并对比两喷嘴撞击流混合器,为优化和改进撞击流混合器结构提供理论依据.
1 计算模型和数值方法
1.1 计算模型
对水平三向撞击流混合器和两喷嘴撞击流混合器进行数值模拟研究.模型结构尺寸如表1所示,物理模型见图1.两种混合器除喷嘴布局外,结构尺寸均相同.两喷嘴混合器喷嘴呈同轴对称布局,水平三向混合器3个喷嘴在混合器中心水平面互成120°分布,如图2所示,3个喷嘴出口与中心圆相切,中心圆的直径即为当量喷嘴间距L.喷嘴间距L=2dN=16 mm.共进行了4组初始速度的模拟研究,进口流速分别为1 m·s-1、2 m·s-1、2.8 m·s-1和4 m·s-1.
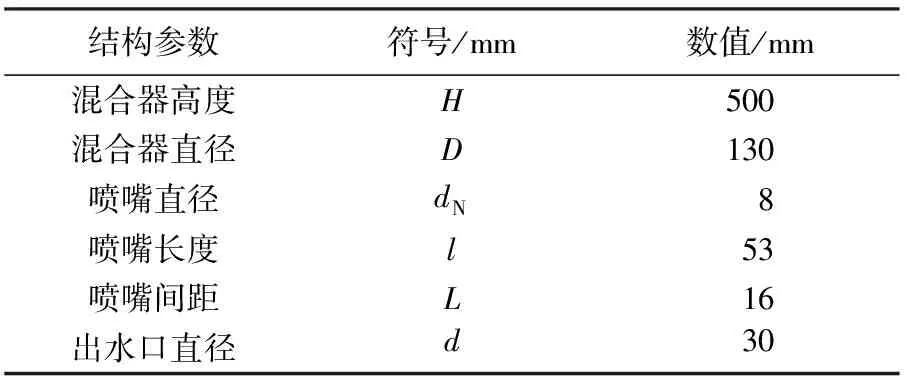
表1 撞击流混合器结构尺寸

图1 混合器物理模型

图2 三喷嘴水平布局示意图
1.2 数值方法
使用CFD软件中的FLUENT进行模拟计算,在前处理软件GAMBIT中完成几何模型和网格划分.采用基于压力的隐式求解器,运用SIMPLEC算法求解压力速度耦合关系,为提高模拟精度,采用2阶迎风格式进行计算.不考虑重力因素,无黏流动,进口边界条件类型定义为VELOCITY-INLET,出口边界类型定义为OUTFLOW.壁面条件:反应器壁面为无滑动光滑壁面.在撞击区域采用Tgrid形式进行网格划分并加密,网格SIZE为1.5,数目为318 524,其余区域为非主要计算区域,采用Cooper形式进行划分,网格SIZE为2.0.模拟介质为20 ℃的水.控制方程采用Realizableκ-ε方程模型.
连续性方程
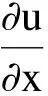
(1)
动量方程


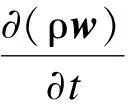
(2)
其中:μ为动力黏度,p为压力,u、v、w是流体在x、y、z三个方向上的速度矢量,Su、Sv、Sw为动量守恒方程的广义源项.
在Realizablek-ε模型中,关于k和ε的输运方程如下:
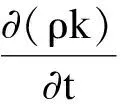
(3)
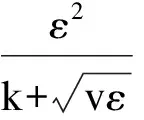
(4)
其中:σk=1.0,σε=1.2,C2=1.9,
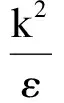

其中:Ωij是从角速度为ωk的参考系中观察到的时均转动速率张量,k为湍动能,ε为耗散率,Gk是由平均速度梯度引起的湍动能k的产生项,C1和C2是经验常数.
2 水平三向混合器与两喷嘴混合器模拟结果分析
2.1 两种混合器径向速度分析
对4种不同初始速度下的模拟结果进行分析,得到两种混合器径向截面速度云图,以初始速度2 (m·s-1)为例进行分析,如图3所示.如无特殊说明,本文所指径向截面均为混合器X-O-Z平面.
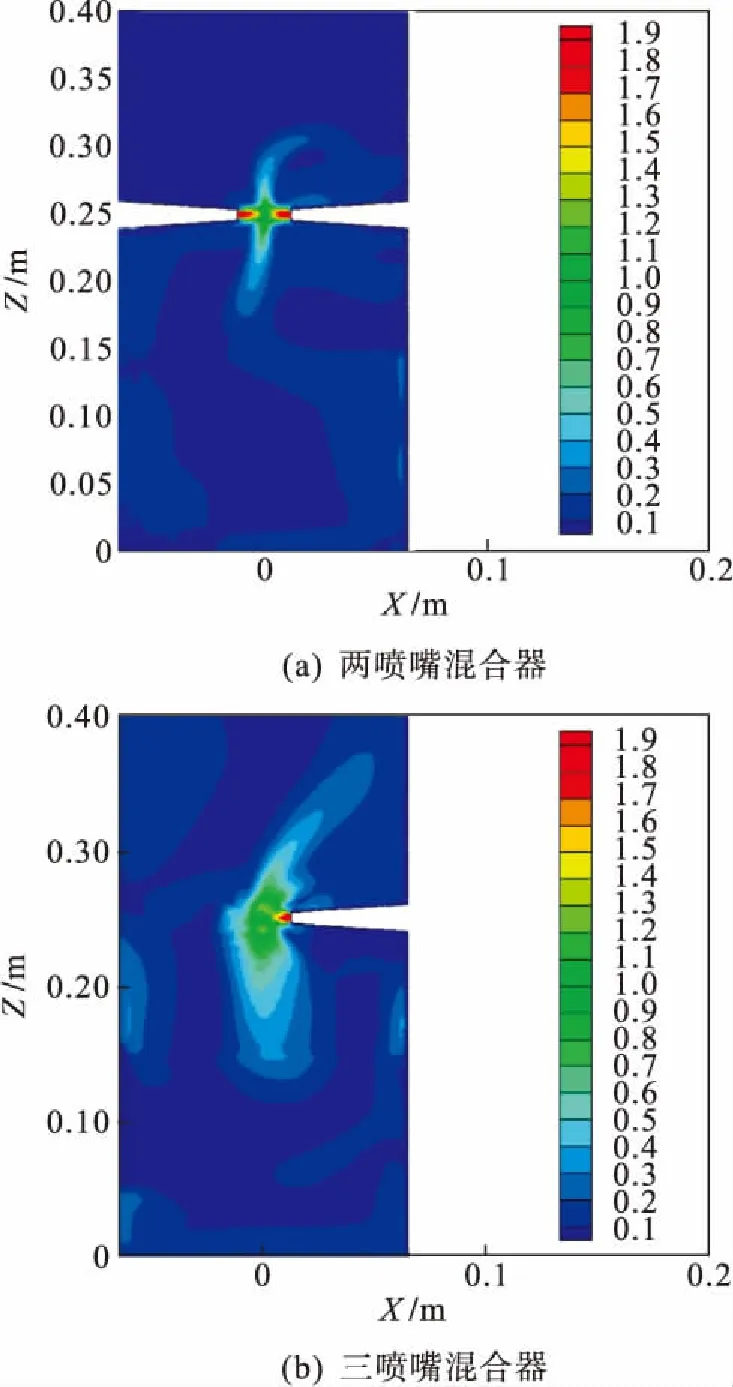
图3 两种混合器径向速度云图
从图3可以看出:三喷嘴混合器的流体在撞击前发展规律与两喷嘴混合器相似,流体相向运动发生撞击时,沿喷嘴轴线方向的流速会在撞击区域迅速减小.由于流体撞击动量比为1,所以在喷嘴轴线中心点形成撞击点,此处为流速的最小值点.对比两混合器径向速度云图,三喷嘴混合器的发展区面积明显较两喷嘴混合器发展区面积大,分析其原因为:撞击后的流体在撞击点处压缩后,转向压力较低的区域发展.两喷嘴混合器由于喷嘴为对称布置,流体沿Z轴呈直线转向径向发展,三喷嘴混合器喷嘴为非对称布局,撞击区域中流体流量更大且流体间相互作用更加剧烈,使撞击后的流体偏离Z轴一定角度转向径向发展,由于流体运动的不稳定性,流体轨迹发生弯曲、扭转[9],从而增大了三喷嘴混合器的发展区,更有利于混合.
为进一步分析径向速度分布规律,在两种混合器Z轴上200~300 mm范围内取等空间步长的50个点,对其径向速度进行数据处理,得到的结果如图4、图5所示.
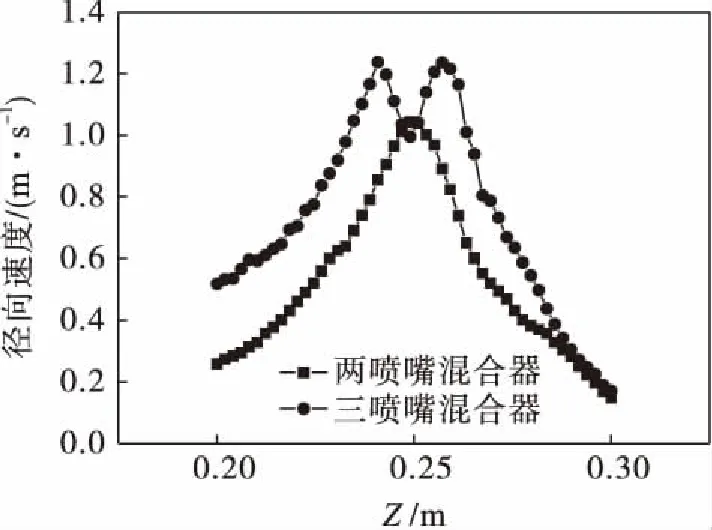
图4 两种混合器径向速度分布曲线
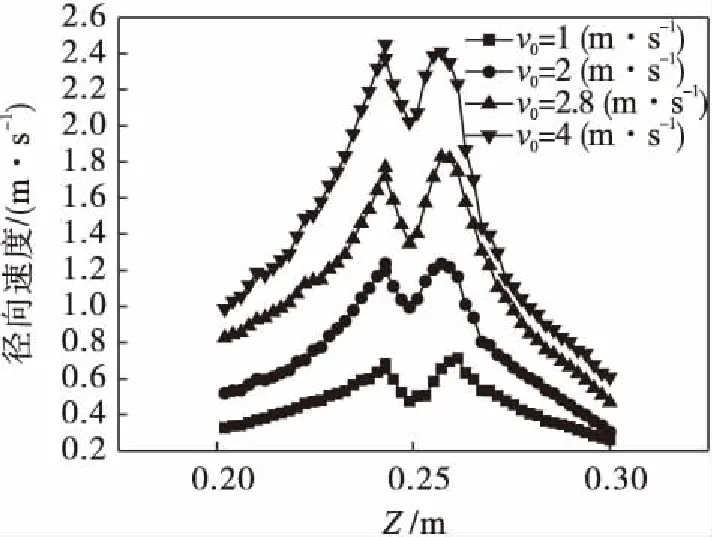
图5 三喷嘴混合器4种初始速度下径向速度分布曲线
图4为初始速度2 (m·s-1)时两混合器径向速度分布曲线,结合图3可知:两喷嘴混合器径向速度呈单峰分布,峰值点即为撞击点;三喷嘴混合器径向速度呈双峰分布,峰值点非撞击点,峰值点在Z轴上关于撞击点上下对称,且在所取点上三喷嘴混合器径向速度均不小于两喷嘴混合器径向速度.分析其原因为:三股流体在撞击前表现为自由圆射流,流体不断与周围静止流体发生卷吸,形成混合层;随着流程增大,混合层边缘部分流体速度被降低,达到撞击区域后未参与撞击,而是与撞击后的径向流体交汇,转向径向发展.因为三股流体动量相等,发生撞击后流体速度大幅减小,相比与参与撞击后转向径向的流体,未参与撞击的混合层流体速度较大,两两交汇后与参与撞击的径向流体汇聚,在一定程度上增大了径向流体的速度,从而在Z轴上形成关于撞击点对称的峰值点.图5为三喷嘴混合器在不同初始速度下径向速度分布曲线,由图5可以看出:随着初始速度的增大,三喷嘴混合器最大径向速度增大,且径向速度峰值位置不随初始速度的增大而改变.
2.2 两种混合器径向湍动能分析
水平三向撞击流混合器径向速度的分布规律必然影响到混合器径向湍流特性.湍动能(k)的大小是比较混合器混合效果优劣的一个标准.对4种初始速度下两种混合器进行模拟计算,以2 (m·s-1)初始速度下的两混合器湍动能分布云图为例进行分析,结果如图6所示.
从图6可以明显看出:两种混合器的湍动能均在撞击点达到最大值;水平三向撞击流混合器的高湍动能区域明显大于两喷嘴对置式撞击流混合器高湍动区域,湍动能区域以喷嘴轴线为轴呈上下对称的椭圆形分布,撞击点即为椭圆中心,长短轴分别位于Z轴和喷嘴所在轴线;且水平三向撞击流混合器湍动能最大值大于两喷嘴对置式混合器湍动能最大值.分析其原因为:相比于两喷嘴混合器,水平三向撞击流混合器在撞击区流量更大,其独特的径向速度规律产生了更大的速度梯度,流体间相互剪切作用更强烈,从而使得三向撞击流混合器撞击区湍动更剧烈,高湍动区域更大,混合效果更好.
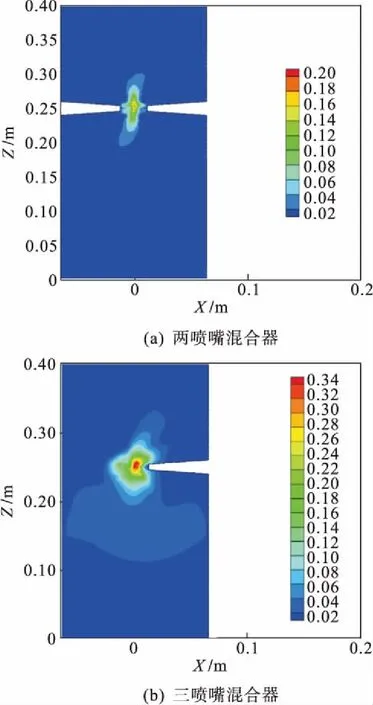
图6 两种混合器径向截面湍动能云图
对该区域进行进一步的研究,以探讨水平三向撞击流混合器湍动能分布规律.在两种混合器Z轴上200~300 mm范围内取等空间步长的50个点,对其湍动能进行数据处理,结果如图7、图8所示.

图7 两种混合器Z轴湍动能分布曲线
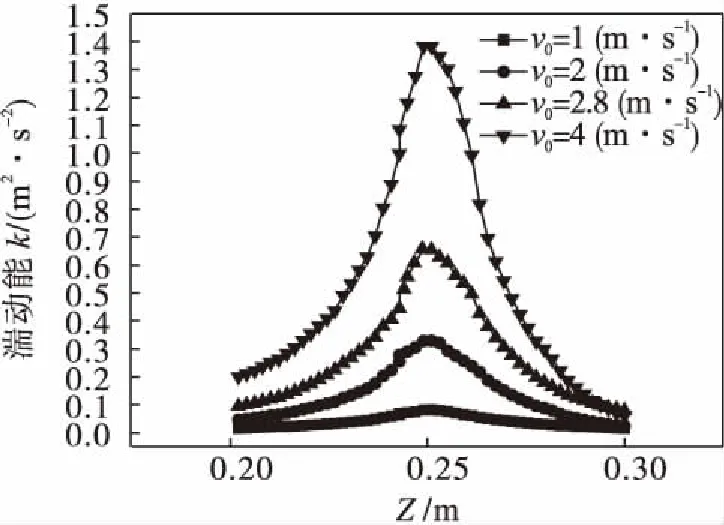
图8 不同初始速度下三喷嘴混合器Z轴湍动能分布曲线
从图7中可以看出:两种混合器湍动能均呈单峰对称分布,峰值点即为撞击点,两种混合器湍动能均在撞击点达到最大值;水平三向撞击流混合器湍动能在所取点范围内均大于两喷嘴混合器,且撞击点附近15 mm范围内的湍动能值均大于两喷嘴混合器的湍动能最大值.对比4种初始速度下三喷嘴混合器湍动能分布曲线,如图8所示,随着初始速度的增大,其湍动能增大幅度明显,表明在撞击区有更大的速度梯度,相对湍流强度增强,更有利于混合器的湍动混合.
对4种初始速度下所得两种混合器湍动能最大值进行二次处理,结果如表2所示.

表2 两种混合器最大湍动能值
在4种工况中,随着初始速度的增大,两种撞击流混合器最大湍动能值逐渐增大,水平三向撞击流混合器湍动能最大值分别为两喷嘴对置式撞击流混合器湍动能最大值的1.57倍、1.89倍、2.03倍和2.21倍,水平三向撞击流混合器的湍动程度更优于两喷嘴对置式.湍动程度的高低影响着混合效果的优劣,相比于两喷嘴对置式撞击流反应器,水平三向撞击流混合器较大的湍动能值和较大的高湍动能区域均证明水平三向撞击流混合器混合效果优于两喷嘴对置式撞击流反应器.
2.3 两种混合器径向湍流耗散率分析
湍流耗散率(ε)是指在分子黏性作用下由湍动能转化为分子热运动动能的速率,通常以单位质量流体在单位时间内损耗的湍动能来衡量,以ε表示,其大小和分布是反应器湍流结构的关键参数,对微观混合效率有直接影响.但前人对水平三向撞击流混合器湍流耗散率的研究还不够完善,为此,通过对径向上湍流耗散率分布规律的研究进行补充.
初始速度为2 (m·s-1)时两种混合器中Z轴上200~300 mm范围内50个点的湍流耗散率分布曲线如图9、图10所示.
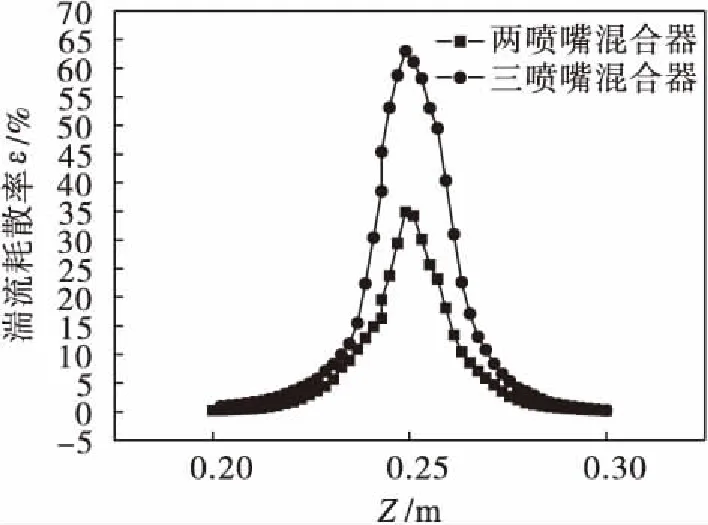
图9 两混合器Z轴湍流耗散率分布曲线
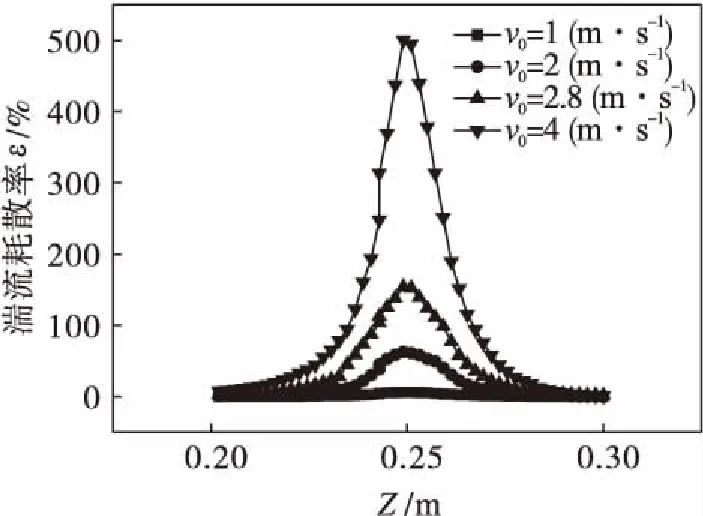
图10 不同初始速度下三喷嘴混合器Z轴湍流耗散率分布曲线
由图9可知:两混合器湍流耗散率分布规律与湍动能分布规律相似,湍流耗散率亦呈单峰分布,峰值点即为撞击点,此处湍流耗散率为最大;径向流体湍流耗散率在发展区衰减曲线以峰值点为中心呈对称分布,在所取点上三喷嘴混合器湍流耗散率不小于两喷嘴混合器.由图10可知:随着初始速度增大,三喷嘴混合器湍流耗散率迅速增大.对两种混合器湍流最大耗散率数值进行二次处理发现,初始速度为1 (m·s-1)时,三向撞击流混合器湍流耗散率最大值为两喷嘴对置式混合器湍流耗散率最大值的1.31倍,2 (m·s-1)时为1.85倍,2.8 (m·s-1)时为1.94倍,4 (m·s-1)时为2.06倍,三喷嘴混合器较大的湍流耗散率对微观混合有更好的影响.
3 结 论
(1) 水平三向撞击流混合器径向速度呈双峰分布,峰值点并非撞击点,峰值点在Z轴上关于撞击点上下对称,三喷嘴混合器径向速度最大值大于两喷嘴混合器径向速度最大值.随着初始速度的增大,三喷嘴混合器最大径向速度值增大,径向速度峰值位置不随初始速度的增大而改变.
(2) 水平三向撞击流混合器湍动能呈单峰分布,峰值点即为撞击点,其高湍动能区域大于两喷嘴对置式撞击流混合器,且关于喷嘴轴线对称,呈椭圆形分布,水平三向撞击流混合器最大湍动能值大于两喷嘴对置式混合器,模拟工况下(初始速度4 m/s)最大达到两喷嘴混合器的2.21倍.
(3) 水平三向撞击流混合器径向湍流耗散率分布与湍动能分布规律相似,呈单峰分布,在撞击点达到最大值.模拟工况下三喷嘴混合器湍流耗散率最大达到两喷嘴混合器的2.06倍.
[1] TAMI A.撞击流反应器:原理和应用[M].伍沅,译.北京:化学工业出版社,1996:21-33.
[2] 伍沅.撞击流-原理·性质·应用[M].北京:化学工业出版社,2005:8-9.
[3] WU Yuan(伍沅),XIAO Yang(肖扬),ZHOU Yuxin(周玉新).Micromixing in the Submerged Circulative Impinging Stream Reactor[J].Chinese J Chen Eng,2003,11(4):420-425.
[4] 肖杨.浸没循环撞击流反应器中的流动与混合[D].武汉:武汉化工学院,武汉工程大学,2002:12-43.
[5] SIDDIQUI S W,ZHAO Y A,KUKUKOVA A,et al.Characteristics of a Confined Impinging Jet Reactor:Energy Dissipation Homogeneous and Heterogeneous Reaction Products and Effect of Unequal Flow[J].Ind.Eng.Chem.Res.,2009,48(17):7945-7958.
[6] SIDDIQUI S W,UNWIN P J,XU Z,et al.The Effect of Stabilizer Addition and Sonication on Nanoparticle Agglomeration in a Confined Impinging Jet Reactor [J].Colloids Surf.A:Phys.Eng.Asp,2009,350(1):38-50.
[7] 孙怀宇,王宇.撞击流反应器的流场测量及数值模拟研究[J].沈阳化工大学学报,2011,25(3):217-219.
[8] 杨侠,刘丰良,毛志慧,等.立式循环撞击流反应器不同撞击间距下混合性能分析[J].化工进展,2012,31(6):1210-1214.
[9] 张建伟,徐成海,伍沅,等.浸没循环撞击流反应器的流场数值模拟[J].东北大学学报(自然科学版),2004,25(2):157-159.
Numerical Simulation of Radial Flow Field in Multi-nozzle Impinging Stream Reactor
ZHANG Jian-wei, LIU Si-yuan, FENG Ying, ZHANG Xue-liang, WANG Nuo-cheng
(Shenyang University of Chemical Technology, Shenyang 110142, China)
In order to optimize the structure of the impinging stream reactor,we use Fluent software to carry out numerical simulation studies for the flow field characteristics of three nozzles impinging stream reactor in different initial speeds,and compare with two nozzles impinging stream reactor.The results show that the radial velocity of three nozzles impinging stream reactor shows the bimodal distribution,and the peak is symmetrical about the point of impact.With the increase of initial velocity,the positions of peak point are not changed.The turbulence kinetic energy and turbulent dissipation rate in radial direction of three nozzle impinging stream reactor show the unimodal distribution,the peak is the impact point.In the same initial speed,the biggest turbulence kinetic energy and turbulent dissipation rate of three nozzle impinging stream reactor is 2.21 and 2.06 times compared with the biggest of two nozzles impinging stream reactor,respectively.In four different initial velocities,distance of the impact point of three nozzle impinging stream reactor within the scope of 15 mm,turbulent kinetic energy values of three nozzle reactor are greater than the biggest values of two nozzle reactor.
impinging stream reactor; numerical simulation; radial velocity; turbulence kinetic energy; turbulent dissipation rate
2015-05-28
国家自然科学基金资助项目(21476141);辽宁省教育厅资助项目(L2012138)
张建伟(1964-),男(满族),辽宁义县人,教授,博士,主要从事新型高效节能过程装备的研究.
2095-2198(2017)01-0050-06
10.3969/j.issn.2095-2198.2017.01.009
TQ021.1
A
