一类二阶离散哈密顿系统的无限多同宿轨
2017-07-19陈梦迪吴海英
陈梦迪,吴海英
(武汉理工大学 理学院,湖北 武汉 430000)
一类二阶离散哈密顿系统的无限多同宿轨
陈梦迪,吴海英
(武汉理工大学 理学院,湖北 武汉 430000)
应用变分法研究了超二次二阶离散哈密顿系统的同宿轨问题。在L(t)允许变号并且b(t)是变号实数的条件下,运用临界点理论得到了该系统具有无限多的同宿轨。借鉴现有研究成果,进一步弱化系统中非线性项的控制条件,仍可得到较好的结果。
同宿轨;离散;哈密顿系统;临界点理论;超二次
0 引言
本文将讨论具有变号位势的二阶离散哈密顿系统
△[p(t)△u(t-1)]-L(t)u(t)+b(t)▽V(u(t))=0, ∀t∈,
(1)
其中:u∈N,N为给定的正整数;△u(t-1)=u(t)-u(t-1);p(t)与L(t)都是N×N实对称矩阵,并且p(t)总是正定的;b(t)为变号实数;V∈C1(N,),V(x)≥0,∀x∈N,▽V(x)为V关于x的梯度。
系统(1)的一般形式是:
△[p(t)△u(t-1)]-L(t)u(t)+▽W(t,u(t))=0, ∀t∈。
(2)
近年来,许多学者将临界点理论运用到离散系统(2)解的研究中。当p(t)≡IN×N,且A(t)≡0时,系统(2)的周期解[1-5]和正解[6-7]不唯一。当N=1时,对于系统(2)的解,已有一些文献报道,例如文献[8]关于周期解的研究;文献[9-11]关于边界值问题的讨论;文献[12-13]得到了系统(2)在N=1和W(t,u)≥0时同宿轨存在性的证明。针对系统(1)也有一些研究,如文献[14]得到了系统(1)在p(t)≡IN×N和A(t)≡0时周期解存在性的证明;文献[15]考虑了在L(t)是正定的且b(t)是变号的情况下系统(1)的同宿轨。文献[16]考虑了L(t)非全局正定且满足条件(L)时,系统(2)同宿轨的存在性:
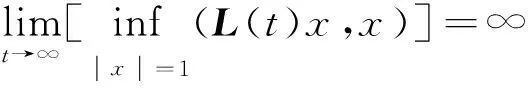
然而,当W(t,u)=b(t)V(u)时,在L(t)非全局正定且在b(t)可变号的情形下,尚未得到同宿轨存在性的结论。为解决这个问题,本文运用临界点理论来研究系统(1)。
1 理论基础
首先,令N1={t∈:b(t)>0},N2={t∈:b(t)≤0},然后给出以下条件:
(Ⅰ)b(t)(t∈)是实数,,且存在n0∈使得b(n0)>0。
(Ⅲ)V∈C1(N,),V(0)=0,且存在c0>0,R0>0使得
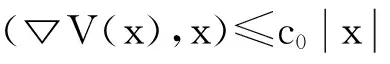
(Ⅳ)存在μ>2及a1>0使得


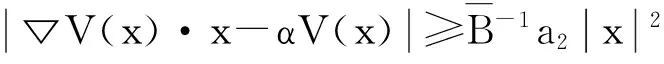

(Ⅵ)V(x)=V(-x),∀x∈N。
2 主要结论
定理1 假设p(t)是N×N实对称的正定矩阵,并且L(t)、b(t)和V满足条件(L)和条件(Ⅰ)~条件(Ⅵ),则系统(1)有无限多非平凡的同宿轨。
由条件(L)知,存在a3>0,使得当t∈N1时,有
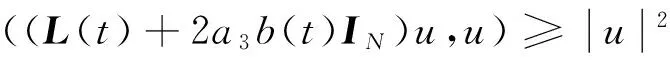
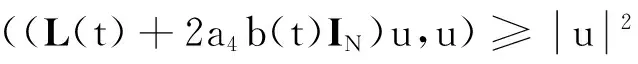

条件(L′)
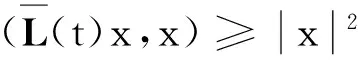
此时系统(1)变为
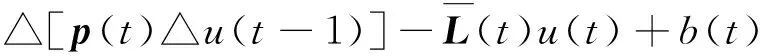
(3)
可知系统(1)和系统(3)的条件是等价的,因此有下面的引理。
引理1 u是系统(1)的解当且仅当它是系统(3)的解。
3 变分框架
令
S={{u(t)}t∈:u(t)∈N,t∈};
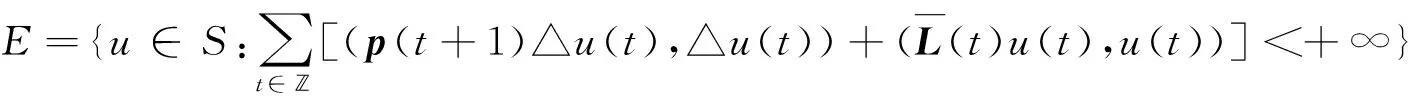
由E的定义可知,对于任意的u,v∈E,有
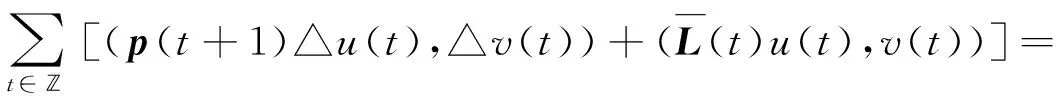
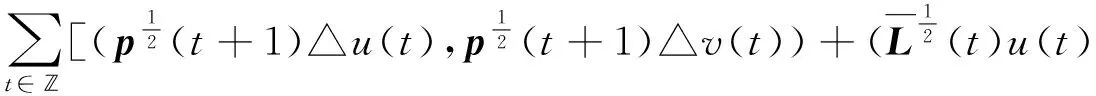
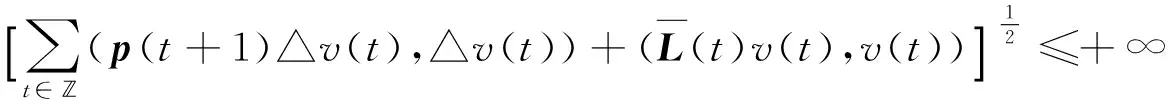
(4)
因此,可在E上定义内积
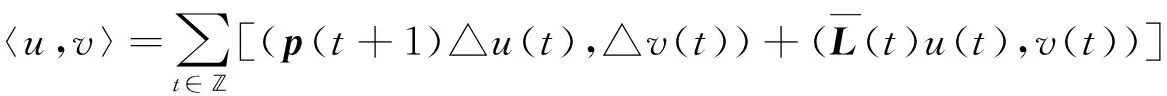
可知(E,〈·,·〉)是希尔伯特(Hilbert)空间,并且相应的范数为

对任意的1≤q<+∞,令
lq(,;
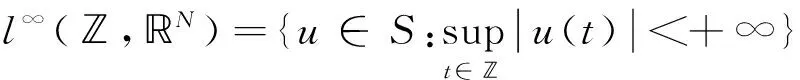
它们的范数分别定义为

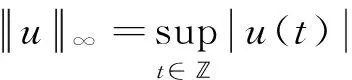
由文献[17]引理2.2和文献[18]引理2.1可知:对所有的2≤q≤+∞,E连续地嵌入到lq(,N),即存在γq>0,使得
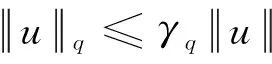
(5)
在E上定义泛函Φ为
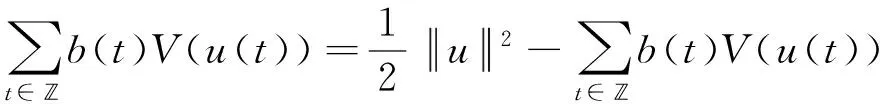
(6)
下面证明Φ∈C1(E,)。
对所有的u∈E,存在N0∈使得当>N0时,,因此由条件(Ⅲ)可知,。
因此,

(7)
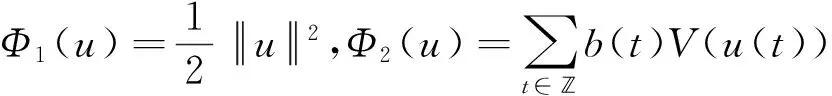
下面证明Φ2∈C1(E,)。
令φ(θ)=Φ2(u+θh),0≤θ≤1,∀u,h∈E,由于V∈C1(E,),
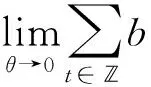
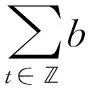
其中:0<ξt<1,则Φ2在E上是Gteaux可微的。

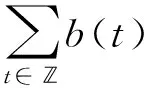

可知Φ2关于u有Gteaux微分算子(E的对偶空间),且有
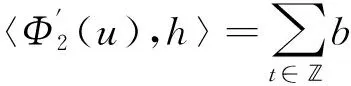
对任意的v=v(t)∈E,∀ε>0,由于V∈C1(E,),那么存在δ>0使得当,进而时
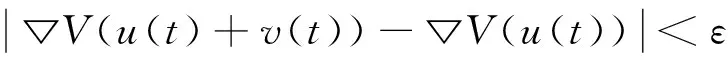
因此,可得
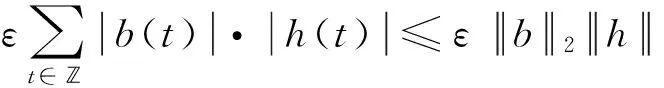

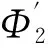
因此,Φ∈C1(E,)且
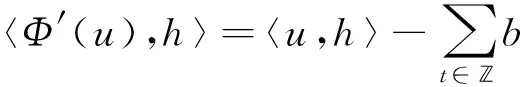

(8)
取k∈,h={h(t)}∈E使得h(k)≠0且对所有的t∈{k},有h(t)=0,则由式(8)可得:
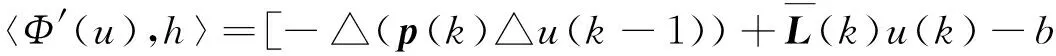
(9)
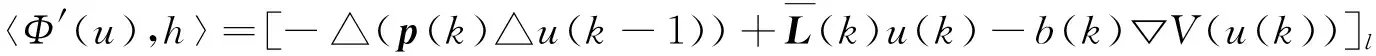
(10)
由k和l的任意性可知,Φ′(u)=0当且仅当

因此,u是Φ的一个临界点当且仅当u是系统(1)的解。

引理2 在定理1的条件下,Φ满足(C)c条件。
证明 假设序列{uk}k∈⊂E使得当k→+∞时Φ(uk)→c>0,〈Φ′(uk),uk〉→0。
首先证明{uk}k∈在E中有界。
由条件(Ⅲ)可知:

(11)
对足够大的k,有
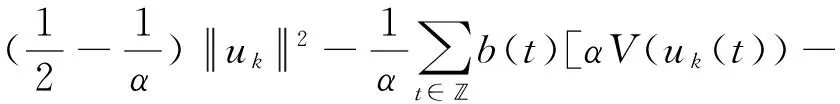
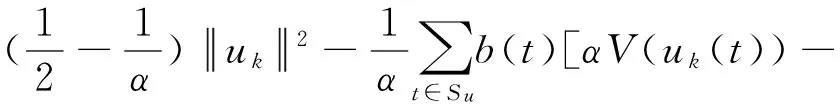
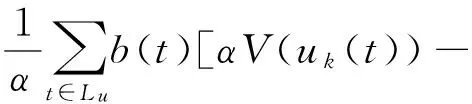
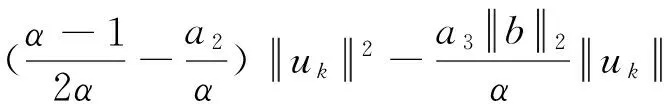
(12)
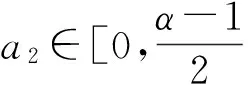
由于E的自反性,uk在E中存在弱收敛的子列,一般地,可假设子列仍为uk且其弱极限为u0。
由于




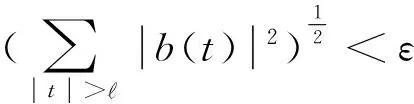
并定义E},那么E是E的有限维子空间并且维数是2N。
令
显然,vk={vk(t)}∈E,v0={v0(t)}∈E。
〈uk,h〉→〈u0,h〉, ∀h∈E,
(13)
取h∈E,则〈vk,h〉→〈v0,h〉,即在E中有。由于E维数有限,根据有限维空间中强收敛和弱收敛的等价性可得,在E中有vk→v0,k→∞,从而在E中有vk→v0,k→∞,并且有

(14)
对足够大的k,
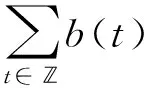
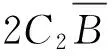
由ε的任意性可得:

(15)
此外,由式(14)可得:

因此有

由ε的任意性、式(8)和式(13)可得:
〈Φ′(uk)-Φ′(u0),h〉→0,k→+∞, ∀h∈E,
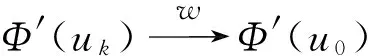
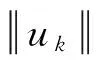
〈Φ′(uk) -Φ′(u0),uk-u0〉= 〈Φ′(uk),uk-u0〉≤
(16)
由式(15)和式(16)可得:
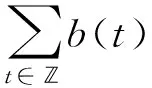
即在E中有uk→u0,k→+∞。证毕。
令{ej}是E的正交基,定义Xj=ej,

(17)
由文献[19]可知,可以找到正整数m≥1,使得:
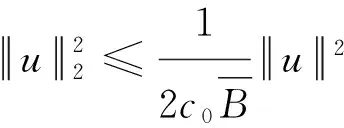
(18)
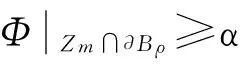
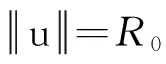
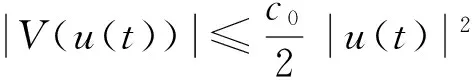
(19)
由式(6)、式(18)和式(19),有:

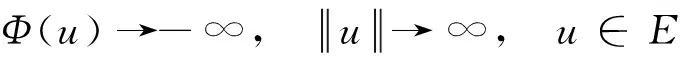
证明 反证法。

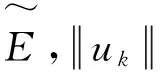
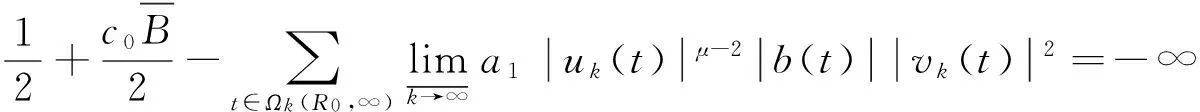
矛盾,故引理4得证。


引理5 令X是Banach空间,X=Y⊕Z,其中Y是有限维的。若I∈C1(X,)满足(PS)条件,且满足:
(I1) I(0)=0,I(-u)=I(u);
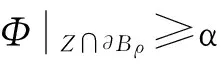
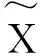
则I有一个无界的临界值序列。
4 主要结论的证明
[1] GUO Z,YU J.Existence of periodic and subharmonic solutions for second-order superlinear difference equations[J].Science in China(series a),2003,46(4):506-515.
[2] RODRIGUEZ J,ETHERIDGE D L.Periodic solutions of nonlinear second-order difference equations[J].Advances in difference equations,2005,2005(2):173-192.
[3] XUE Y F.Existence and multiplicity of periodic solutions for second-order discrete Hamiltonian systems[J].Journal of southwest China normal university,2006,31(1):7-12.
[4] XUE Y,TANG C.Existence of a periodic solution for subquadratic second-order discrete Hamiltonian system[J].Nonlinear analysis,2007,67:2072-2080.
[5] BIN H,YU J,GUO Z.Nontrivial periodic solutions for asymptotically linear resonant difference problem[J].Journal of mathematical analysis and applications,2006,322(1):477-488.
[6] AGARWAL R P,PERERA K,O’REGAN D.Multiple positive solutions of singular and nonsingular discrete problems via variational methods[J].Nonlinear analysis,2004,58(1/2):69-73.
[7] AGARWAL R P,PERERA K,O’REGAN D.Multiple positive solutions of singular discretep-Laplacian problems via variational methods[J].Advances in difference equations,2005,2005(2):93-99.
[8] YU J,GUO Z,ZOU X.Periodic solutions of second order self-adjoint difference equations[J].Journal of the London mathematical society,2005,71(1):146-160.
[9] YU J,GUO Z.Boundary value problems of discrete generalized Emden-Fowler equation[J].Science in China(series a),2006,49(10):1303-1314.
[10]YUJ,GUOZ.OnboundaryvalueproblemsforadiscretegeneralizedEmden-Fowlerequation[J].Journalofdifferentialequation,2006,231(1):18-31.
[11]LIANGH,WENGP.Existenceandmultiplesolutionsforasecond-orderdifferenceboundaryvalueproblemviacriticalpointtheory[J].Journalofmathematicalanalysisandapplications,2007,326(1):511-520.
[12]MAM,GUOZ.Homoclinicorbitsandsubharmonicsfornonlinearsecondorderdifferenceequation[J].Nonlinearanalysistheorymethods&applications,2007,67:1737-1745.
[13]MAM,GUOZ.Homoclinicorbitsforsecondorderself-adjointdifferenceequation[J].Journalofmathematicanalysisandapplications,2006,323(1):513-521.
[14]YUJ,DENGX,GUOZ.PeriodicsolutionsofadiscreteHamiltoniansystemwithachangeofsigninthepotential[J].Journalofmathematicanalysisandapplications,2006,324(2):1140-1151.
[15]TANGX,CHENJ.InfinitelymanyhomoclinicorbitsforaclassofdiscreteHamiltoniansystems[J].Advancesindifferenceequations,2013,2013(1):242.
[16]DENGX,CHENGG.HomoclinicorbitsforsecondorderdiscreteHamiltoniansystemswithpotentialchangingsign[J].Actaapplicandaemathematicae,2008,103:301-314.
[17]LINX,TANGX.ExistenceofinfinitelymanyhomoclinicorbitsindiscreteHamiltoniansystems[J].Journalofmathematicanalysisandapplications,2011,373(1):59-72.
[18]TANGX,LINX.InfinitelymanyhomoclinicorbitsfordiscreteHamiltoniansystemswithsubquadraticpotential[J].Journalofdifferenceequationsandapplications,2013,19(5):796-813.
[19]WILLEMM.Minimaxtheorems[M].Boston:Birkhäuser,1996.
国家自然科学基金项目(51179146);教育部人文社会科学基金项目(12YJAZH022)
陈梦迪(1990-),女,河南许昌人,硕士生;吴海英(1966-),女,通信作者,湖北武汉人,副教授,博士,硕士生导师,主要研究方向为泛函分析和应用统计.
2016-09-11
1672-6871(2017)06-0074-08
10.15926/j.cnki.issn1672-6871.2017.06.015
O177.91
A
