带渐消因子的容积卡尔曼滤波算法

贺 姗，师 昕

（西安工程大学计算机科学学院，陕西 西安 710048）

带渐消因子的容积卡尔曼滤波算法

贺 姗，师 昕

（西安工程大学计算机科学学院，陕西 西安 710048）

在实际的非线性系统滤波问题中，会出现模型不匹配的情况，而标准容积卡尔曼滤波器对于这种模型不确定性的鲁棒性比较差，其滤波估计后的效果会出现较大的偏差。针对这个问题，结合强跟踪滤波器的思想，提出了一种新的带渐消因子的容积卡尔曼滤波算法。这个算法的主要思想是，在滤波过程中，引入渐消因子修正滤波器的状态协方差矩阵。应用这种方法能够获得比容积卡尔曼滤波更高的滤波精度。

非线性系统；强跟踪滤波；容积卡尔曼滤波；卡尔曼滤波

在状态估计中，如果为非线性系统，通常采用扩展卡尔曼滤波（Extended Kalman Filter，EKF）。这个算法的主要思想是，通过对系统的非线性方程进行泰勒级数展开，截取一阶项或二阶项对非线性函数进行线性化近似，再通过卡尔曼滤波器处理。2009年，Arasaratnam提出了容积卡尔曼滤波（Cubature Kalman Filtering，CKF），它是一种确定点采样滤波算法。然而在实际应用过程中，可能出现系统初始状态建模不准确的问题。

针对这个问题，周东华等人提出了强跟踪滤波器。强跟踪滤波器应对系统产生的状态突变等问题，该方法的滤波精度比较高。随后，在周东华等人提出的强跟踪滤波算法的基础上，又提出了一系列的改进算法，例如扩展卡尔曼滤波强跟踪算法（Strong Tracking Extended Kalman Filter，SEKF）滤波。

该算法通过引入强跟踪滤波因子修正滤波器的状态预测协方差矩阵，具有较强的跟踪性。本文将强跟踪滤波器算法应用到了容积卡尔曼滤波器算法中，提出了带渐消因子的容积卡尔曼滤波算法。

1 带渐消因子的容积卡尔曼滤波

针对滤波过程中出现的模型不确定性问题，基于前人所提出的强跟踪滤波算法，可以得到一种改进的滤波方法，即带渐消因子的容积卡尔曼滤波算法。该算法可以有效克服模型的不确定性。一个滤波器具有强跟踪性能的充分条件是需要满足正交性原理。正交性原理是，一个滤波器要成为强跟踪滤波器的充分条件是，在线选择一个适当的时变增益矩阵，从而得出：

式（1）中：γk为量测估计值与量测真实值间的误差（残差）。

当出现系统模型不匹配的情况时，需要在线调整时变增益矩阵，让残差序列仍然保持正交性，使得滤波器仍能满足正交性原理，能够保持较强的跟踪能力。为了使得滤波器具有强跟踪滤波器的特性，可以引入一个时变的渐消因子λ。具体实现方法是，在强跟踪容积卡尔曼滤波的预测误差协方差阵中引入渐消因子，而量测更新部分与标准容积卡尔曼滤波算法相同，此处不再赘述。

算法1是在线求解渐消因子λ，即：

式（2）中：ρ为遗忘因子，0.95≤ρ≤0.995；lk为弱化因子，lk≥1.

第一步，初始状态协方差因式分解：

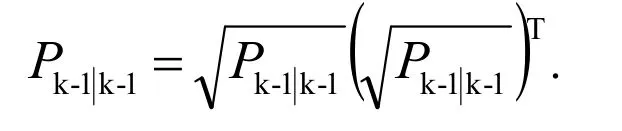
第二步，计算积分点：

第三步，计算修正之后的积分点，得到新的积分点Xl，k-1│k-1.

第四步，计算增值积分点：

第五步，计算公式（3），得到估计状态，然后计算公式（4），得到预测误差协方差：

2 仿真实验和结果分析

针对单变量非稳定增长模型（Univariate Nonstationary Growth Model，UNGM），可得：

3 结论

针对非线性系统滤波问题，本文结合相关学者提出的强跟踪滤波算法，提出了带渐消因子的容积卡尔曼滤波算法。针对容积卡尔曼滤波对于模型不确定性的鲁棒性比较差这一问题，利用强跟踪滤波器在线调整增益矩阵，使得系统输出的残差序列仍然保持正交，则可以使得滤波器在实际系统中具有更强的跟踪性能。

实验仿真的结果表明，与标准容积卡尔曼滤波器相比，本文提出的带渐消因子的容积卡尔曼滤波算法，能够获得更高的滤波精度，均方根误差比较小。

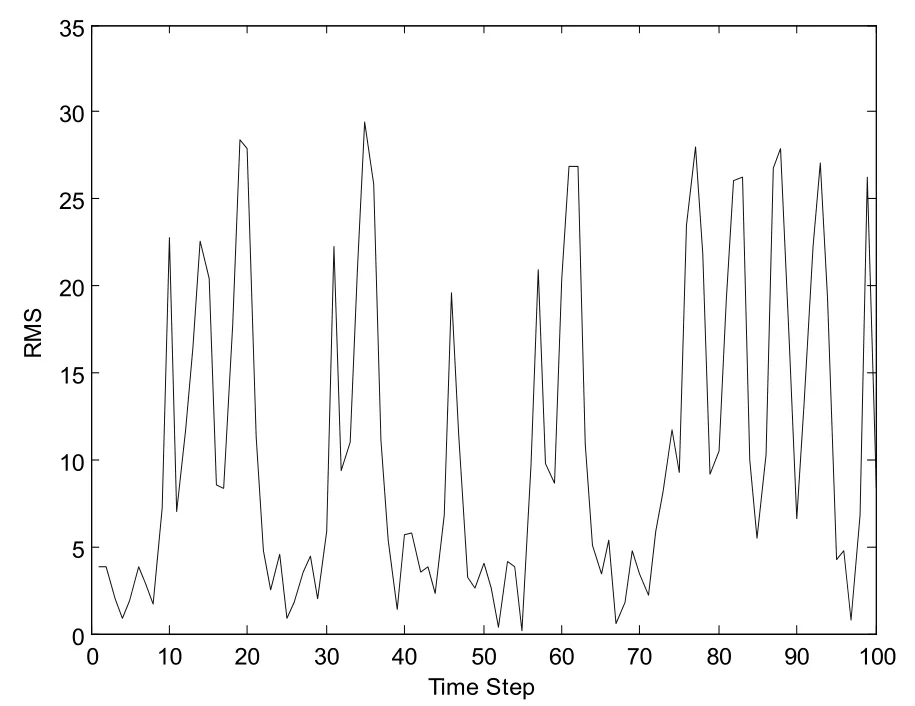
图1 容积卡尔曼滤波算法估计误差

图2 强跟踪容积卡尔曼滤波算法估计误差

［1］PS Maybeck，EJ Balder.Book-Review-Stochastic Models Estimation and Control.Space Science Reviews，1980，26（8）：868-869.

［2］Arssaratnam I，Haykin S.Cubature Kalman filters.IEEE Trans onAutomatic Control，2009，54（6）：1254-1269.

［3］周东华，席裕庚，张钟俊.非线性系统的带次优渐消因子的扩展卡尔曼滤波［J］.控制与决策，1990，5（5）：1-6.

［4］周东华，席裕庚，张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器［J］.自动化学报，1991，17（6）：690-695.

［5］付梦印，邓志红，闫丽萍.Kalman滤波理论及其在导航系统中的应用［M］.北京：科学出版社，2010：100-103.

［6］范文兵，刘春风，张素贞.一种强跟踪扩展卡尔曼滤波器的改进算法［J］.控制和决策，2010，21（1）：74-76.本文部分参考文献因著录项目不全被删除。

〔编辑：白洁〕

TN97

A

10.15913/j.cnki.kjycx.2017.13.001

2095-6835（2017）13-0001-02