基于NSGA-Ⅱ的电动汽车充电站多目标优化规划

韩克勤，丁丹军，钱科军，戴康，蔡吉人，周辉，张新松

（1.国网江苏省电力公司苏州供电公司，江苏苏州215004；2.南通大学电气工程学院，江苏南通226019）

基于NSGA-Ⅱ的电动汽车充电站多目标优化规划

韩克勤1，丁丹军1，钱科军1，戴康1，蔡吉人1，周辉2，张新松2

（1.国网江苏省电力公司苏州供电公司，江苏苏州215004；2.南通大学电气工程学院，江苏南通226019）

发展电动汽车（Electric vehicle，EV）是落实国家低碳经济发展战略、促进资源节约型、环境友好型社会建设的重要举措。当前，各国政府都非常重视EV的发展，美国能源部将设立20亿美元政府资金资助下一代EV需要的电池和部件开发；德国计划到2030年拥有600万辆EV；日本计划到2020年，EV占日本市场的50%。工信部《电动汽车发展战略研究报告》预测，2030年全国EV保有量将达到6 000万辆。现有技术水平下，EV主要通过电网充电，随着未来EV的大规模普及，充电网络将成为配电系统中的重要新增负荷，将对电力系统的规划、运行、调度、控制和电力市场运营产生不可忽视的影响［1—3］。

EV需要利用电网补充能量，因此，充电网络是发展EV的重要基础设施之一，其是否完善在很大程度上决定了电动汽车车主使用的便利性。若充电网络规划不合理，将直接阻碍EV的推广，并对配电系统的运行产生影响。目前，EV充电网络规划研究主要集中于EV充电站的选址和定容两个子问题［4—5］。文献［6］首先建立了EV充电负荷模型，并在此基础上提出了以对潮流影响最小化为目标的EV充电站选址模型与方法。文献［7］综合考虑了充电站建设运营成本和充电者充电成本，构造了基于充电站综合成本最小的充电网络规划模型。文献［8］根据网格划分思想提出了一种充电站选址和定容方法，以充电总成本最小为依据选址，以充电站总充电功率为依据定容。文献［9］综合考虑多种因素，建立了充电网络规划的最大收益模型，并采用粒子群算法和加权伏罗诺伊图对其进行了求解，得出充电站的最优建设地址与建设容量。文献［10］提出了一种基于云重心理论的EV充电站选址规划评估方法，该方法能综合处理定量指标和定性指标，从而确定充电站的最优建站地址。然而，上述文献均未全面考虑EV充电站作为公共服务设施的特性，从而导致规划模型中的规划目标单一，规划结果参考价值不大。

针对以上问题，本文综合考虑EV充电站作为公共服务设施以及大型用电设施的双重特性，提出了同时考虑充电网络充电服务能力（即截取车流量）最大化与配电网络损耗最小化的充电网络多目标优化规划模型，并考虑了包括配电网络电压偏差约束在内的一系列约束条件。上述模型具有截取车流量最大与配电系统网络损耗最小两个不同维度的优化目标，是典型的多目标优化问题。本文采用改进的非支配排序遗传算法（Non-dominated sorting genetic algorithm II，NSGA-II）［11］对其进行求解，获得了该多目标优化问题的帕累托解集。帕累托解集由一系列非劣解组成，可为规划人员提供全面的参考。最后，以25节点交通网络［12］对和IEEE33节点配电系统［13］对为例，对所提出的模型及算法进行验证。

1 EV充电网络规划模型

1.1 目标函数

与加油站网络一样，充电站网络是保障车主出行的重要公共服务设施，因此，确保其服务能力最大化是充电网络规划的首要目标，本文以充电站建成之后所能截获的车流量Fc为依据衡量其服务能力，因此，充电网络规划模型存在以下的优化目标

式中：Q为交通网络中所有线路q的集合；yq为表征线路q上车流量能否被充电网络截获的二进制变量，“1”表示可被截获，“0”表示不被截获；fq为线路q上的车流量，可由重力空间互动模型求出，该模型如下式所示

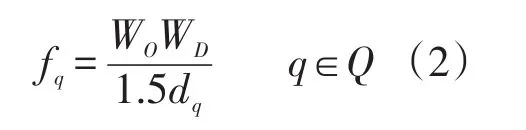
式中：WO为线路q起点O的权重；WD为线路q终点D的权重；dq为线路q的距离。

除做为公共服务设施外，EV充电站还是配电网络中的大型用电设施，其接入电网将对配电网络的电能质量和经济性运行产生显著影响，主要体现为网络损耗的增加与节点电压幅值的偏移两方面。因此，本文所提的充电网络规划模型中将网络损耗Floss最小作为另一个优化目标，如下式所示

式中：Ploss,i为配电网络中支路i的功率损耗；n为支路数；Pi为支路i末端的有功负荷，Qi为无功负荷；Ui为支路i末端电压；Ri为支路i电阻。

1.2 约束条件

1）充电站个数约束

考虑到市政规划中土地资源较为紧张，为避免资源浪贾，提高土地利用率，在规划中应限制充电站建设数目，如下所示

式中：Xi为表征是否在节点i是否建设充电站的二进制变量，取1表示该节点建设充电站，“0”表示不建设；N为规划的充电站个数。

2）充电站容量约束

显然，充电网络中充电站的总容量应能满足该规划区域所有电动汽车的充电需求，即存在如下约束

式中，Wi为节点i建设的充电站容量；Wmax为规划区域最大充电需求。

3）电压偏移约束

对配电网络来说，充电站接入不仅可导致网络损耗增加，还将改变配电网络的电压分布，进而可能影响对电力用户供电的电能质量，因此，电压偏移必须限制在一定范围之内，即存在如下所示的电压偏移约束

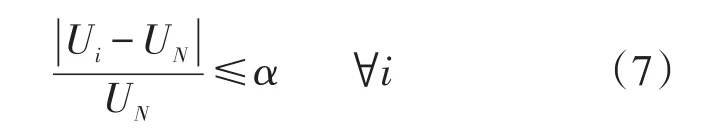
式中：Ui为节点i电压；UN为配电网络的额定电压；α为允许的最大电压偏移。

4）对配电网络来说，线路输送功率必须小于其输送极限，否则将导致配电设备的温度超过最高允许温度，因此，存在如下输送功率约束

式中：Pl为线路l的有功功率；Pl,max为线路i允许流过的最大功率。

2 基于NSGA的模型求解

如上文所示，本文提出的EV充电网络规划模型具有充电服务能力最大化与配电网络损耗最小化两个不同维度的优化目标，是典型的多目标优化问题，其数学上的最优解为一系列非劣解组成的帕累托解集。传统的遗传算法（genetic algorithm，GA）很难对此类多目标优化问题进行求解，本文采用NSGA-Ⅱ算法对其进行求解。与常规GA相比，NSGA的最大特色在于选择操作［15］，即选择操作中基于非支配排序原理对种群中的个体进行分类、排序，下文将对此问题进行详细描述。

2.1 染色体编码

与传统GA一样，编码是应用NSGA-Ⅱ求解优化问题的基础，本文采用如图1所示的编码方案对优化问题进行编码。如图所示，染色体长度取为交通网络节点总数n，码位i的取值j代表了在交通节点i处建设第j类充电站，若可建设的充电站有k类，则j=1，2，3，…，k。显然，图1所示的染色体对应于一个充电网络建设方案。

图1 染色体编码示意图

2.2 遗传操作算子

NSGA-Ⅱ的遗传操作与传统GA大致相同，其最大的特点在于选择操作。假定规模为Npop的种群按非劣解等级分类可分为m层，层次索引越小，非劣解层等级越高［16］。对个体i来说，若其所处的非劣解层次为j，则该个体的适应Vfit,i为

显然，同一非劣解层次上的个体适应度相同，称之为共享适应度，为使优化结果在目标空间中均匀分布，需要对个体在各自非劣解层中的局部拥挤距离进行计算，局部拥挤距离计算如图2所示，用id表示，其取值为在个体i周围包含个体i本身但不包含其他个体的最小的矩形的两条边之和。

在共享适应度以及局部拥挤距离计算的基础上，采用轮赛制选择算子进行选择操作，即从父代中随机选取2个个体，若共享适应度值不同，则选取共享适应度大的个体，若共享适应度值相同，则选择局部拥挤距离大的个体。上述选择操作重复进行，直至形成子代种群。

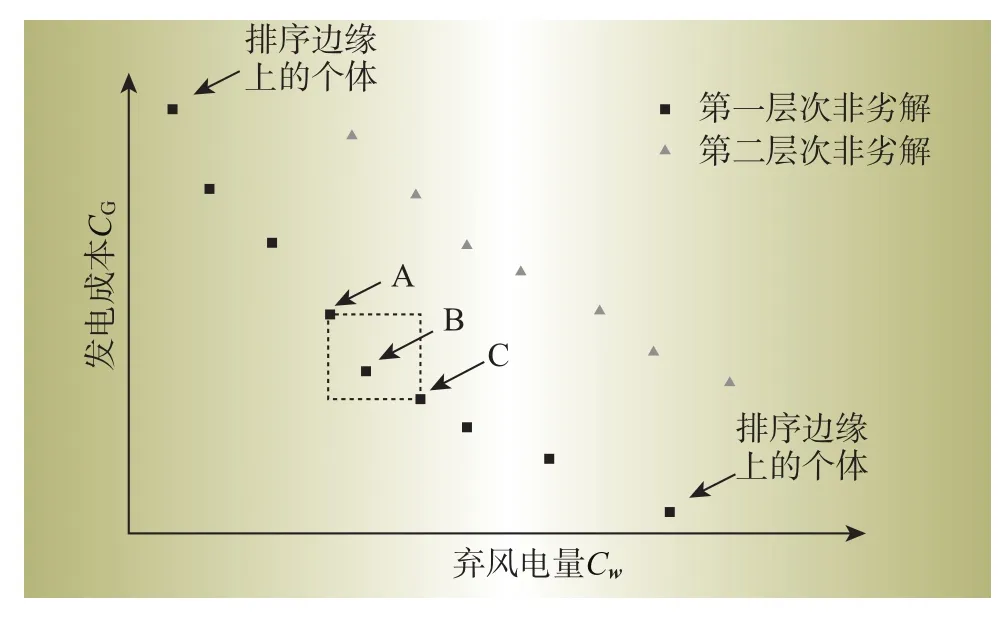
图2 局部拥挤距离计算

2.3 模型求解流程

首先，随机生成一个父代种群P0，并将所有个体按非支配关系排序且指定一个适应度值，然后，采用选择、交叉、变异算子产生下一代种群Q0，大小为Npop；接着将新种群Q0与父代P0合并成R0，种群规模为2Npop，对R0进行非支配排序，产生一系列非支配集Fi，并计算拥挤度，此时第一层非劣解集F1中包含的个体是R0中最优的，将F1放入下一代种群P1中，若F1中个体数小于Npop，则继续向P1中添加下一层非劣解集F2，使P1中个体数量达到Npop，若超出，则根据F2中个体的拥挤度从大到小进行排序，取前Npop-||P1个个体；迭代进行以上步骤，直至达到事先设定的最大进化代数Gmax。图3为算法流程图。

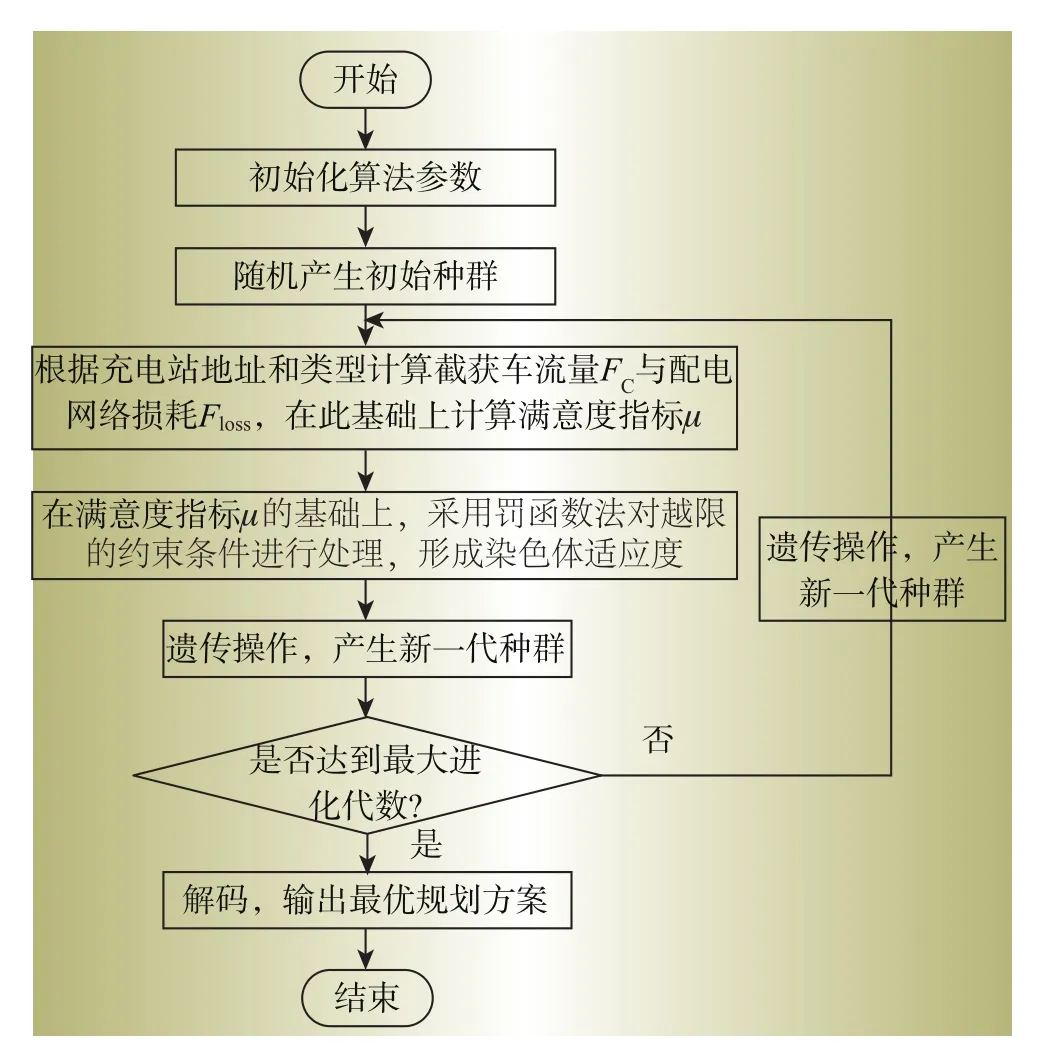
图3 算法流程图

3 算例分析

3.1 算例介绍

以图4、5所示的25节点交通网络与IEEE33节点配电系统为例对文中所提的充电网络多目标规划模型及求解算法的有效性进行验证。

设置电动汽车满电状态下最大行驶路程L=120 km；允许建设的充电站个数N=4；可供选择的充电站容量为0.1、0.2、0.3、0.4 MW4种，染色体编码时分别用1、2、3、4代表；最大充电负荷需求Wmax设为0.8 MW；允许的最大电压偏移量α设为10%；交通节点的权重系数如表1所示。

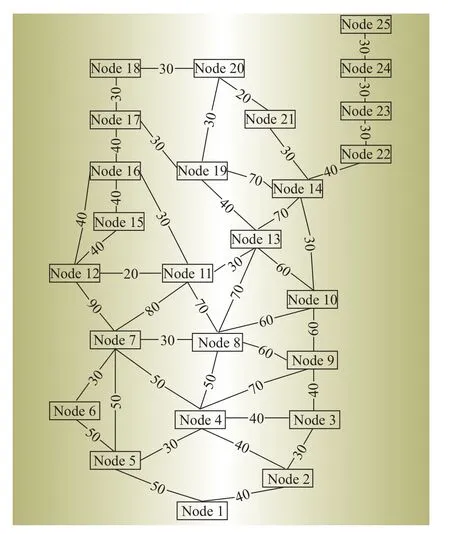
图4 25节点交通网络

图5 IEEE33节点配电系统

表1 交通节点权重系数

3.2 基于NSGA-Ⅱ的算例系统仿真结果

按照上文描述的编码方案，染色体长度n=25，此外，初始种群规模Nnop=50，最大进化代数Gmax设为120，交叉率pc=0.5，变异率pm=0.2。表2给出了由NSGA-Ⅱ求解得到的Pareto最优解集，图6给出了NSGA-Ⅱ初始代、第60代以及进化终止时的非劣解集。

NSGA-Ⅱ收敛特性如图6所示。从图6可看出，NSGA-Ⅱ进化过程中，种群朝着Pareto最优解的方向不断进化，说明算法具有较好的收敛性。

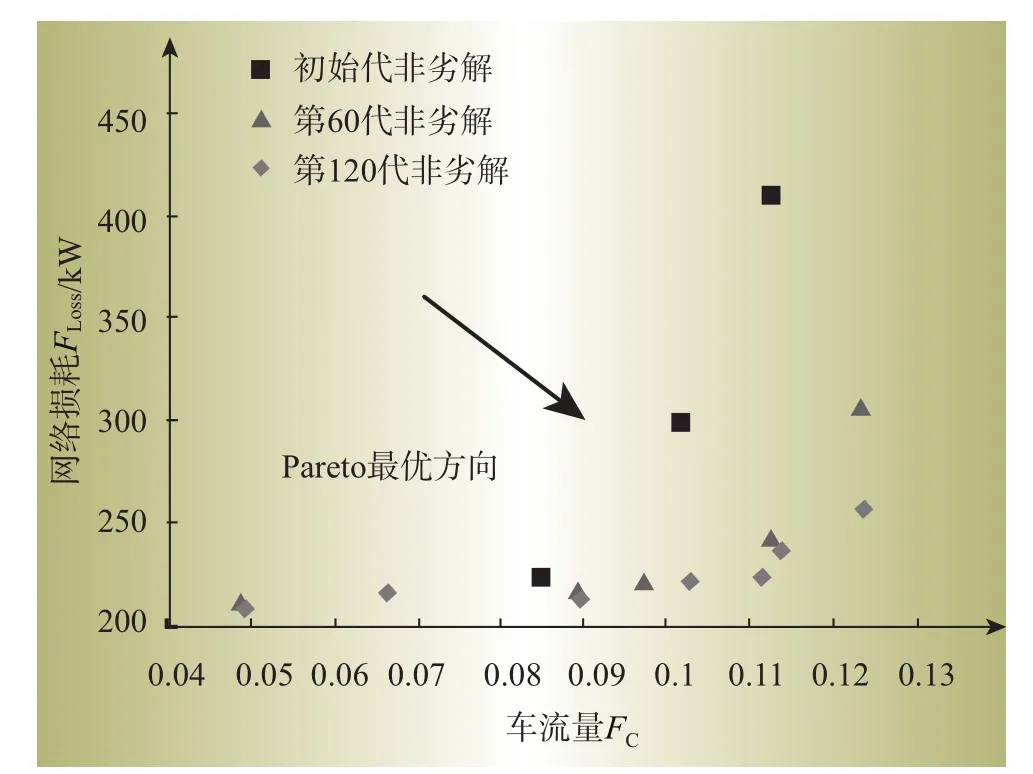
图6 NSGA-Ⅱ收敛特性

由表2可以看出，NSGA-Ⅱ求解得到的Pareto最优解集由7个非劣解组成，解1对应的EV充电网络所能截获的车流量FC=0.123 6（约占总交通网络中总车流量的40.6%），此时，网络损耗Floss也较大，为258.283 0 kW；解7对应的Fc=0.048 8，Floss= 212.507 8 kW，可见，该方案所能截获的车流量较小，但是配电系统中的网络损耗却有所降低。

另外，从表2还可以看出，本文所提规划模型中2个优化目标不存在必然的联系，并且在一定程度上相互冲突，难以同时达到最优，常规优化方法很难得到令人满意的结果，而本文所提的优化方法很好的解决了这一问题，最后给出了一个Pareto最优解集供规划人员参考，规划人员可在Pareto最优解集的基础上确定最终的规划方案。图为NSGA-Ⅱ收敛特性。

表2 算例系统的Pareto最优解集

4 结束语

本文提出了一种同时考虑充电网络服务能力最大化与配电网络损耗最小化的多目标充电网络规划模型，并采用NSGA-Ⅱ算法对其进行了求解，获得了该多目标优化模型的Pareto最优解集。基于25节点交通网络和IEEE33节点配电系统的仿真结果验证了本文所提模型及其算法的有效性。

与一般的EV充电网络规划模型给出一个理论上的最优解不同，本文所提多目标规划模型及其算法可以给出一个Pareto最优解集，规划人员可根据实际情况合理的选择一个最优规划方案，因此，本文所做的研究工作更符合实际，为规划人员提供更多的参考。D

［1］Boulanger A G,Chu A C,Maxx S,et al.Vehicle Electrification:Status and Issues［J］.Proceedings of the IEEE,2011,99（6）:111 6-113 8.

［2］王锡凡，邵成成，王秀丽，等.电动汽车充电负荷与调度控制策略综述［J］.中国电机工程学报，2013，33（1）：1-10.

［3］高赐威，张亮.电动汽车充电对电网影响的综述［J］.电网技术，2011，35（2）：127-131.

［4］任玉珑，史乐峰，张谦，等.电动汽车充电站最优分布和规模研究［J］.电力系统自动化，2011，35（14）：53-57.

［5］WANG Hengsong,HUANG Qi,ZHANG Changhua,et al. A novel approach for the layout of electric vehicle charging station［C］.Proceedings of 2010 International Conference on Apperceiving Computing and Intelligence Analysis,Chengdu,China:IEEE,2010:64-70.

［6］郭建龙，文福拴，袁军，等.电动汽车充电站在配电系统中电气接入点的最优选择［J］.电力建设，2017，38（1）：1-7.

［7］冯超，周步祥，林楠，等.电动汽车充电站规划的多种群混合遗传算法［J］.电力系统及其自动化学报，2013，25（6）：123-129.

［8］GE Shaoyun,FENG Liang,LIU Hong.The planning of electric vehicle charging station based on grid partition method［C］.2011 International Conference on Electrical and Control Engineering,Yichang,China:IEEE,2011: 2726-2730.

［9］唐现刚，刘俊勇，刘友波，等.基于计算集合方法的电动汽车充电站规划［J］.电力系统自动化，2012，36（8）：24-30.

［10］彭泽军，兰剑，陈艳，等.基于云重心理论的电动汽车充电站选址方法［J］.电力建设，2015，36（4）：1-7.

［11］王秀丽，李淑慧，陈皓勇，等.基于非支配遗传算法及协同进化算法的多目标多区域电网规划［J］.中国电机工程学报，2006，26（12）：11-15.

［12］HODGSON M J.A flow capturing location-allocation model［J］.Geographical Analysis,1990,22（3）:270-279.

［13］SINGH D,MISRA R K,SINGH D.Effect of load models in distributed generation planning［J］.IEEE Trans on Power System,2007,22（4）:2204-2211.

［14］Heydt G T.The impact of electric vehicle deployment on load management strategies［J］.IEEE Transactions on Power Apparatus and Systems,vol.PAS-102,no.5, pp.1253-1259,1983.

［15］高媛.非支配排序遗传算法的研究与应用［D］.杭州，浙江大学，2006.

［16］张新松，郭晓丽，周辉，等.基于多目标优化的日前风电接纳研究［J］.南方电网技术，2016，10（1）：60-67.

［17］Kalyanmoy D,Amrit P,Sameer A,et al.A fast and elitist multi-objective genetic algorithm:NSGA-II［J］. IEEE Transactions on Evolutionary Computation［J］. 2002,6（2）:182-197.

［18］王辉，王贵斌，赵俊华，等.考虑交通网络流量的电动汽车充电站规划［J］.电力系统自动化，2013，37（13）：63-69.

Multi-objectivechargingnetwork planningfor electric vehiclesbasedon NSGA-Ⅱ

HAN Ke⁃qin1,DING Dan⁃jun1,QIAN Ke⁃jun1,DAI Kang1,CAI Ji⁃ren1,ZHOU Hui2,ZHANG Xin⁃song2
（1.State Grid Jiangsu Power Company Suzhou Power Supply Company,Suzhou 215004,China；2.School of Electrical engineering,Nantong University,Nantong 226019,China）

电动汽车充电站既是公共服务设施又是配电网络中的大型用电负荷，构建了同时考虑充电服务能力最大与配电网络损耗最小的电动汽车充电网络优化规划模型。该模型为典型的多目标优化模型，采用改进非支配排序遗传算法对其进行了求解，获得了Pareto最优解集。基于25节点交通网络和IEEE33节点配电系统的仿真结果验证了本文所提模型及其算法的有效性。

充电网络规划；多目标优化；非支配排序遗传算法；Pareto最优解

Electric vehicles（EV）charging stations are not only public facilities,but also large⁃scale electricity load demands in distribution network.As a result,an EV charging network plan⁃ning model is proposed in this paper to maximize charging service capacity and to minimize energy losses in distribution systems.The planning model proposed here is a typical multi⁃objective optimal formulation,and the non⁃dominated sorting genetic algorithmⅡ（NSGA⁃Ⅱ）is utilized to obtain Pareto optimal result set of the for⁃mulation.The simulation results based on the 25⁃node traffic net⁃work and IEEE 33 node distribution system verify that the pro⁃posed model and corresponding resolving algorithm are effective.

charging network planning;multi⁃objective opti⁃mization;NSGA⁃Ⅱ;Pareto optimal result

10.3969∕j.issn.1009-1831.2017.S1.026

F407.61

B

2017-03-09