基于层次分析法和模糊理论的液氨泄漏风险研究

周德红，王浩然，2，李文，冯豪

1.武汉工程大学资源与土木工程学院，湖北 武汉 430074；2.仙桃职业学院计算机科学技术学院，湖北 仙桃 433000

基于层次分析法和模糊理论的液氨泄漏风险研究

周德红1，王浩然1，2，李文1，冯豪1

1.武汉工程大学资源与土木工程学院，湖北 武汉 430074；2.仙桃职业学院计算机科学技术学院，湖北 仙桃 433000

采用层次模糊数学理论评价法对液氨企业进行定性和定量的风险评估，从员工的不安全行为、设备设施的不安全状态、安全管理的缺陷、不良的作业环境4个方面构建液氨泄漏事故原因的阶级层结构模型，研究分析事件发生泄漏原因的影响水平，并进行综合性的评判.以液氨使用企业为例，运用该模型可分析出不同企业的安全优劣等级和共同存在的泄漏风险特征.提出应完善企业法律法规定性指标检测的方法、提升员工的专业知识和技术水平、强化生产工艺系统和储罐系统定期与不定期安全检查的力度、建立设备的维修及更新淘汰机制、加强人工智能化检测的建设实现人与科技的双控防范的措施.

液氨泄漏；阶层结构模型；模糊理论；层次分析法风险评估

液氨是企业生产的基础材料，使用非常普遍，在各个行业都有重要的应用.由于市场的需求量大，企业生产的自动化、连续化，给液氨企业带来巨大经济效益.同时，液氨泄漏的事故每年也层出不穷.由于液氨独有的特性，发生泄漏能给周围很大范围内的人员、财产、生态环境带来十分严重的后果.由于液氨泄漏的事故发生的偶然性、不确定性、泄漏原因的复杂性，给人们的安全生产、生活带来了极其的不便［1］.针对液氨泄漏的事故进行全面的分析、考虑各类影响的因素，构建可靠的阶级层次结构模型，并结合MATLAB程序编程计算确定各评价指标的权重［2］.最后结合模糊数学理论构建风险评判模型.该评价方法全面评价了液氨泄漏风险的可能性.既体现了评价过程对客观事物复杂性、多样性的定性和定量分析，又尽可能减少了个人的主观性和局限性.

1 层次模糊数学理论构建的风险评判模型

1.1 评价指标体系的选取

依据液氨泄漏的致因全面分析，尽量选取少的定量、定性指标来反映全面的信息.指标的选取遵循国家的标准、法规以及企业规章制度等，还需详细理解保护对象的主要特点［3-4］.

可以从人员的不安全行为、设备的不安全状态、安全管理的缺陷、环境的不良因素四个方面分析建立指标体系：

一是人员（P1），可从业务技术水平（X1）、职业素质（X2）、安全意识（X3）、违章操作（X4）、岗位变动（X5）等来分析.

二是设备设施（P2），可从生产工艺系统（X6）、消防系统（X7）、储罐系统（X8）、安全辅助系统（X9）、设备安全使用规范（X10）、应急报警系统（X11）、浓度检测预警系统（X12）等来分析.

三是安全管理（P3），可以从安全投入（X13）、安全教育（X14）、专职安全的规章制度（X15）、安全预案的演练（X16）、安全专职机构的业务能力（X17）、安全组织和培训（X18）等来分析.

四是环境（P4），可从车间布局（X19）、作业环境（X20）、工作环境（X21）、企业文化（X22）等来分析.

在现实的评价操作过程中，选取应按照实际情况随机应变的运用，对上述的指标，适当的增减.

1.2 评价指标权重的确定

在全面评价中，各因素成分的权重的分配关乎整个评价成效的高低.利用层次分析法原理来实现决策过程中各个因素的权重的有效分配，从而构建出科学、合理的评价模型.在模型中把难以解决的问题具体化，这些成分又根据本身的属性和从属关系形成阶级层.层次分析分为单层和多层，这里研究二级层次分析［5-6］.

判断矩阵A=(aij).aij反映元素i与元素j对比的标度.判断矩阵的定义如表1所示.

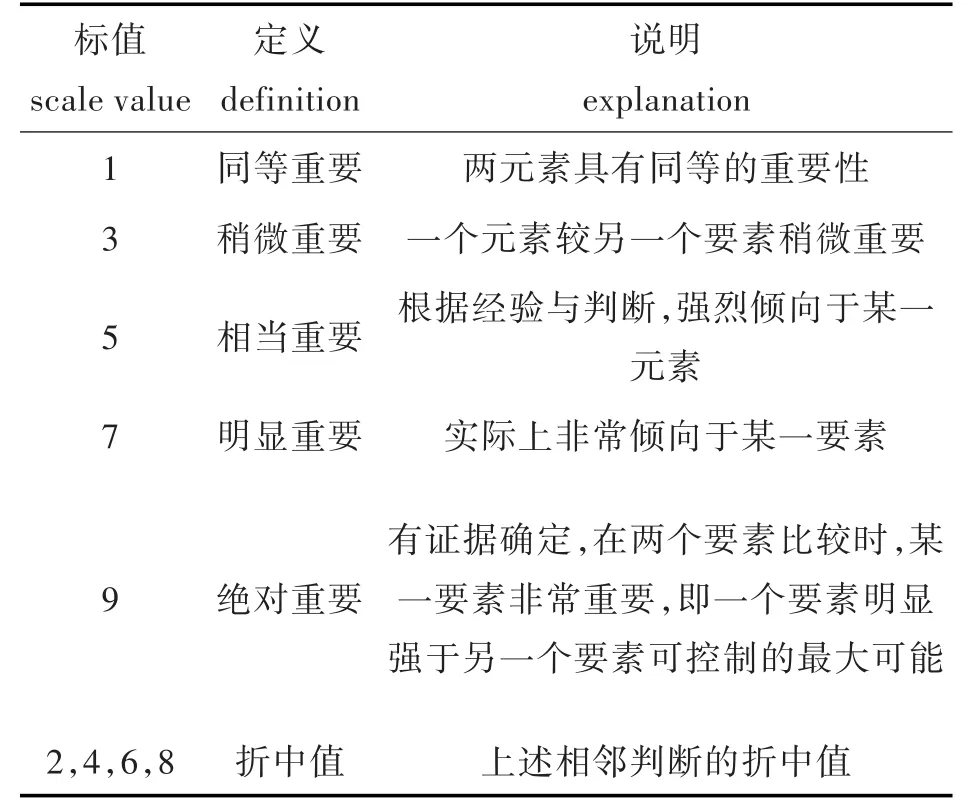
表1 判断矩阵的定义Tab.1Definition of judgment matrix

针对液氨泄漏风险评价的目标，构造出准则层各成分依据表1量化出上一级层次的某成分对下一级层次相关成分的相对重要性［7］.按照两两元素比较的结果，即用数字直观的表达出来，并写出判断距阵.

按行计算矩阵元素的乘积Mi（i=1，2，…，n），运算公式为然后计算Mi的n次方根值，公式为

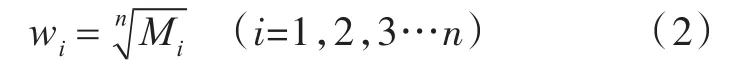
式（3）中：wi为各个元素的权重值.

判断距阵A的λmax.利用MATLAB进行程序的编程计算λmax.

判断距阵是评判者依靠本身的认知、履历的积累给出的判断，很难避免误差的存在.因此，需要对评价指标进行一致性的查验.公式为

再计算CR，计算公式为式（5）中CR=0时，矩阵A能完全满足设计的要求.当CR<0.1时，矩阵A较好的完成一致性的查验要求.如果矩阵不能完成上述指标查验的条件，应重新对各个因素进行再次相对重要度评价，直到判断矩阵完成一致性指标查验为止.

RI平均随机一致性如表2所示.

表2 平均随机一致性Tab.2Average random consistency

1.3 模糊数学评价

该模型方法是凭借模糊数学的理论，把难以量化的、模糊不清的、非定量的问题等价为定量的评价.即用该模型解决受多成分互相影响的对象或目标，给定一个针对性强、成果清晰的综合评判.本文建立二阶的评价模型.

1.3.1 建立因素集按照液氨评价风险指标选取的原则，成立因素集，即

评价集是决策者对对象或目标可能做出评判结果的集合.从研究实际情况出发，取n=5，即评价的结果主要分为5类

V1（0.85～1）为优秀可以认为达到本质安全的级别.

V2（0.75～0.85）为良好（可以认为达到较（非常）安全的级别.

V3（0.60～0.75）为及格可以认为达到安全生产的级别.

V4（0.55～0.60）为不及格可以认为存在安全隐患，需要排除隐患.

V5（0～0.55）为差可以认为必须停产整顿，责令整改.

1.3.2 各因素的权重（w）的确定利用阶层结构模型，来进行诸多因素的权重集w的构建.

1.3.3 隶属矩阵的建立隶属度函数的构建包含定性与定量指标的运算.

1）对于非定性或可量化的指标构建的隶属矩阵是指对n个不同的涉氨企业m个指标组成的：

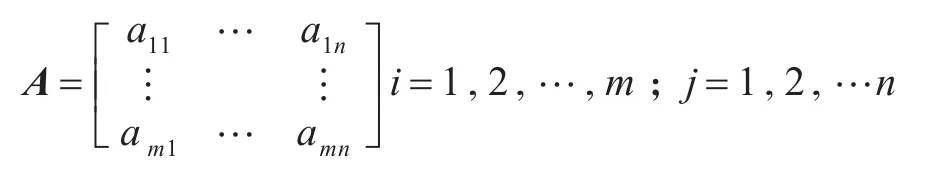
非定性的指标或可量化的指标可采用梯形分布函数的升半梯形分布归一化处理，从而获得对象或者目标相对隶属度矩阵U.计算公式如下：

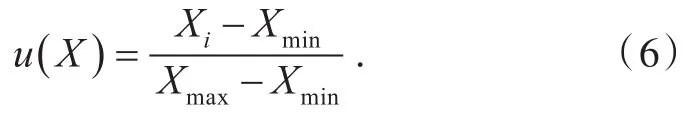
式（6）中Xmin，Xmax各自为第i评价指标中的最小值和最大值.

采用公式（6）进行归一化处理，可得矩阵U为

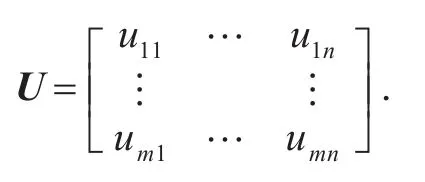
2）对于非定量的指标和难以量化的指标，运用相对二元比较法［8-10］.

目标集中的目标元素Xi与Xj相比：

①若Xi比Xj重要，则令排序标度eij=1，eji=0；

②若Xj比Xj同等重要，则令eij=0.5，eji=0.5；

由此可得到二元比较矩阵E.

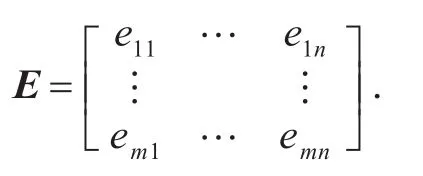
当0≤eij≤1，eij+eji=1，eij=eji=0.5(i=j)时，称矩阵E为二元比较矩阵.eij为目标i对j作二元比较时，目标i对于j的重要性模糊标度；eji为目标j对于i的重要性模糊标度.目标集中的不同元素在进行最优评价时，无法精确的定量描述.因此只有用模糊语言来形容优劣的概念.因此需借助排序，查语气算子与定量标度表（见表3）.令语气算子标度为u，隶属度选取为（1-u）/u.

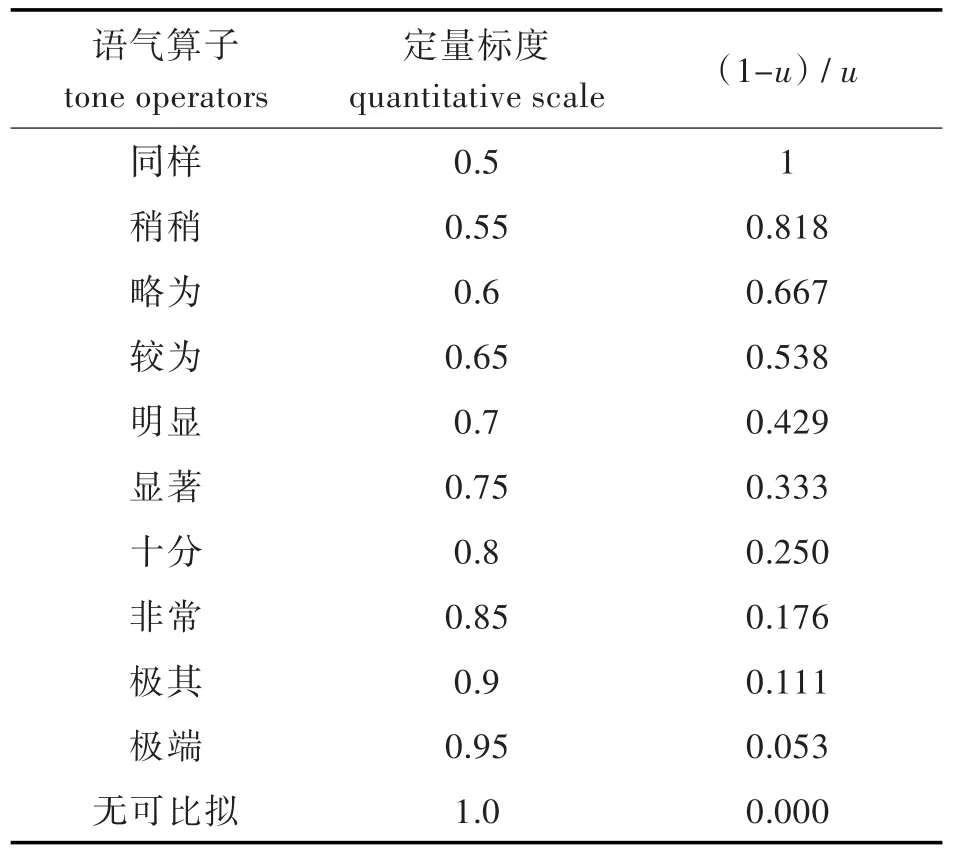
表3 相对隶属度关系表Tab.3Relative membership degree

1.4 综合评价

由上述评价指标构建的隶属度距阵U、因素权重分配集采用矩阵的运算可得到目标集的综合评价向量为：

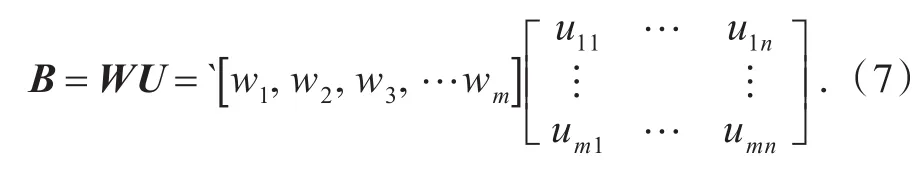
式（7）中，W为阶层结构模型确定权重值，U为评价指标构建的模糊矩阵，B为综合评价向量.

综合评价方法的模型，可以针对合成氨企业液氨泄漏的风险进行评价、安全等级的划分，为预测事故发生的可能性做出依据.综合评价结果可根据评价语集进行安全类型排序的划分.

2 工程实例

以湖北省某化工园区的合成氨企业为例，采用上述综合模型的方法对4家企业（企业M、企业N、企业O、企业Q）进行液氨泄漏风险的评价［10-13］.研究区域不同涉氨企业专家评价打分的结果，如表4所示.

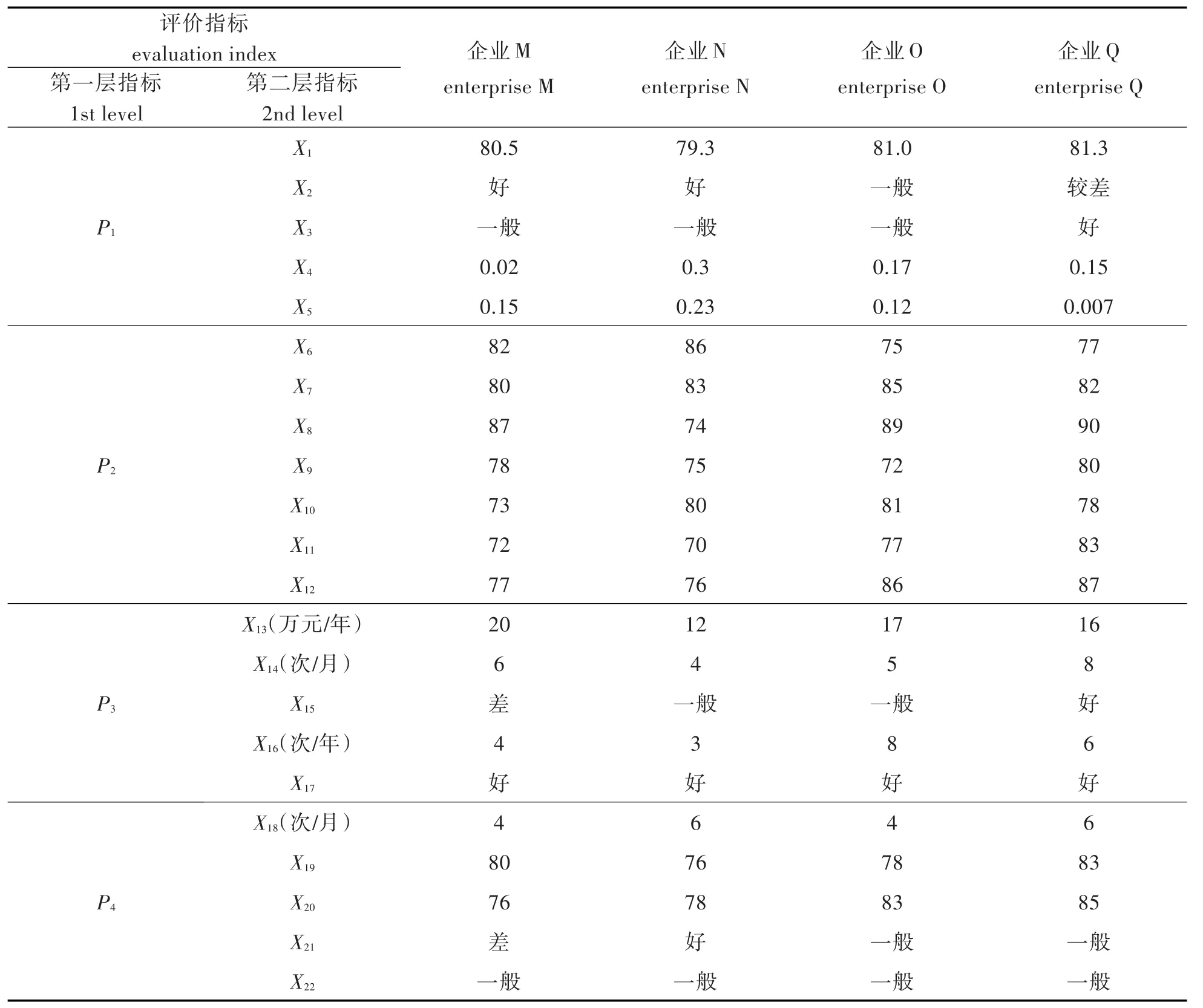
表4 不同涉氨企业综合评价的结果Tab.4Results of comprehensive evaluation of different ammonia related enterprises

2.1 评价指标权重的确定

利用阶层结构模型，成立上下层不同成分的相互评比结果如表5所示.

表5 相互评比结果Tab.5Judgment matrix

根据式（1）和式（2）计算因素权重的近似值wi：

利用公式（3）作规范归一化可得评价因素权重即

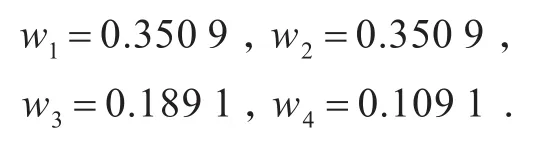
再采用MATLAB计算判断矩阵A的λmax，可得4.009 8.根据公式（4）、（5）进行一致性指标判断.

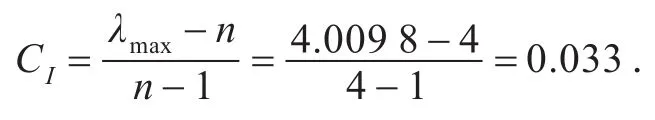
通过查表2可得RI=0.89，则一致性比率为

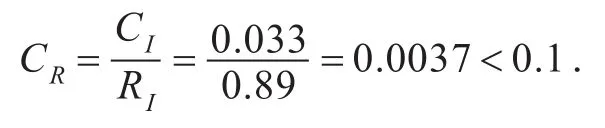
由此可知，各个权重满足一致性的要求，可以接受.

同理，可得各二级指标的权重如下：

对上述指标进行查验，均满足要求.因此各项指标权重均可接受.即可得出综合指标的权重值如表6所示.

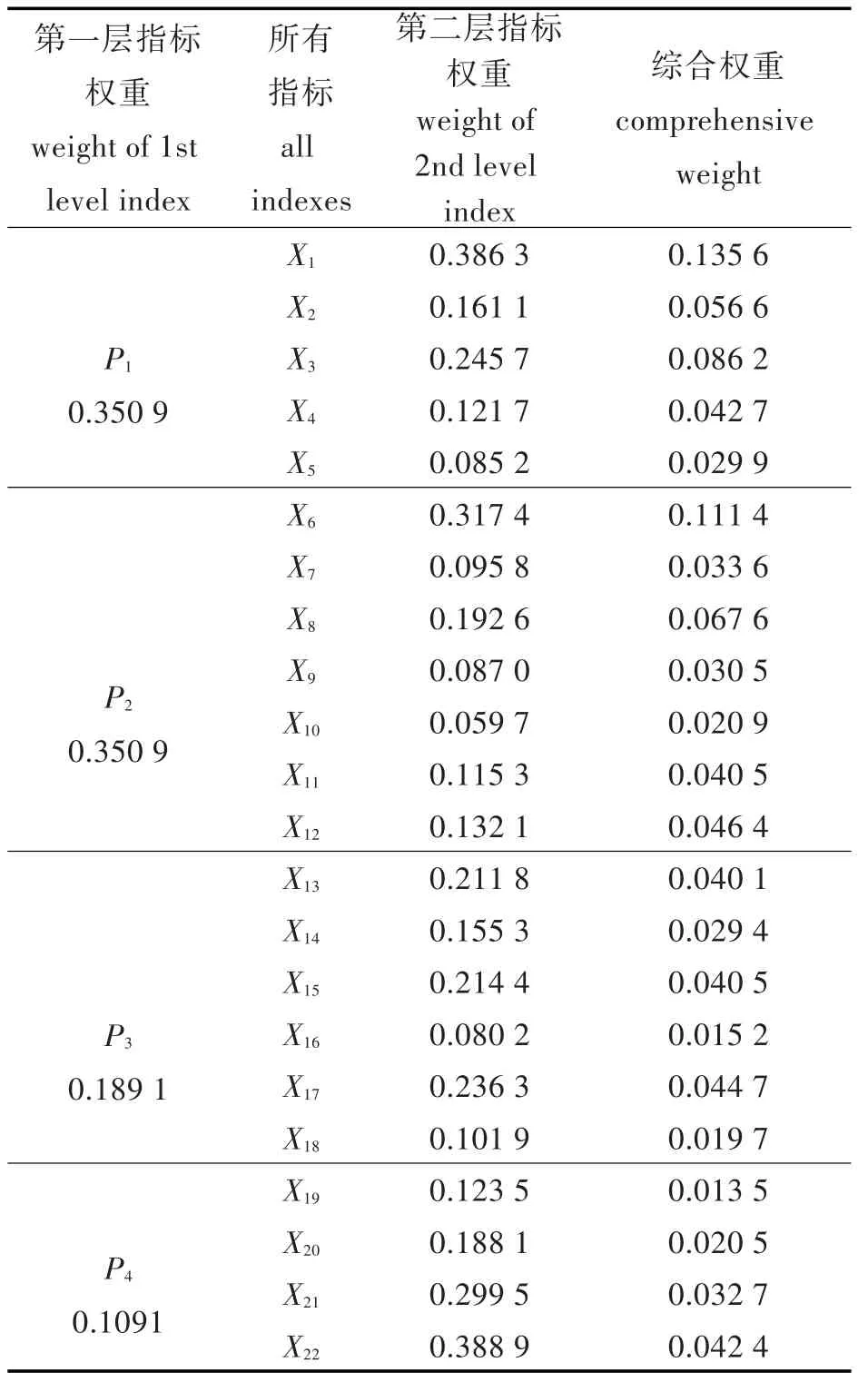
表6 综合指标的权重Tab.6Weight of comprehensive index

2.2 隶属矩阵的确定

评价体系由定量和定性指标组成的特征向量矩阵［14-15］.

1）采取相对二元比较法，对不同涉氨企业综合评价的结果中的定性指标进行量化：

①根据不同涉氨企业的员工的职业素质高低，可得特征向量矩阵.

②根据各企业的员工安全意识高低，可得

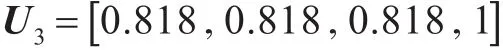
③根据各企业的专职规章制度完善的情况，可得

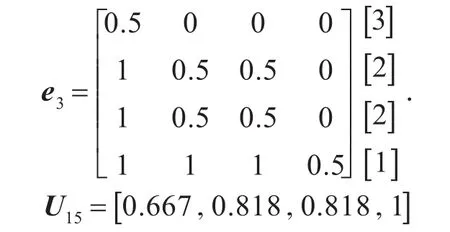
④根据安全专职机构的业务能力的大小，可得

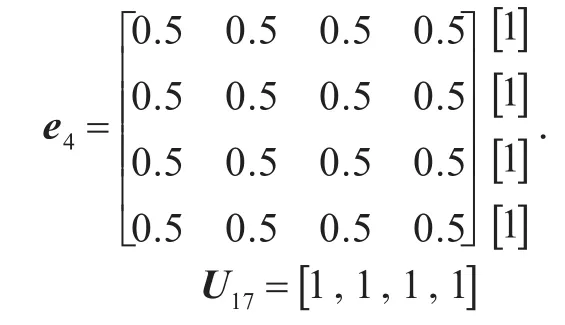
⑤根据工作环境的氛围的好坏，可得

⑥根据企业文化的建设和底蕴，可得

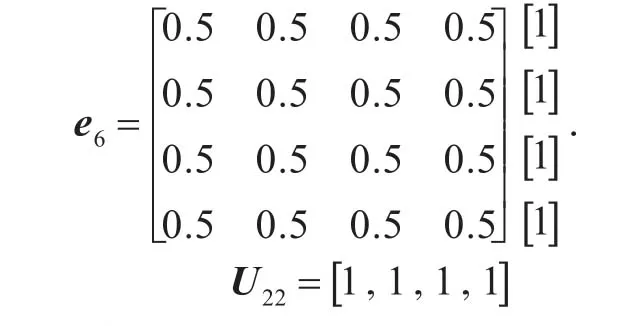
2）采用公式（6）对可量指化指标归一化处理，在结合上述定性指标的隶属度距阵，可得出总的隶属度矩阵.

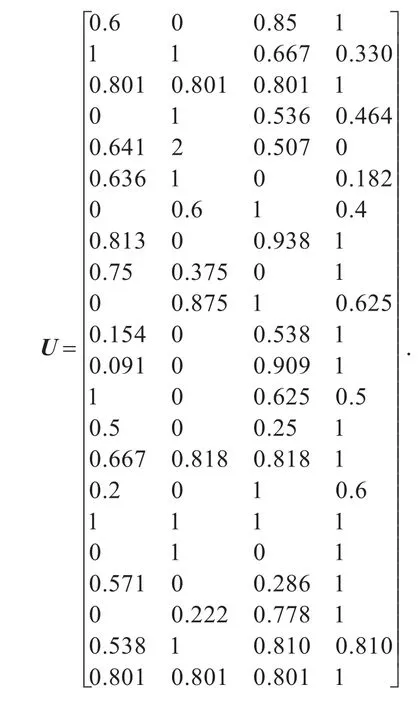
2.3 研究区域风险的综合评价

根据公式（7）可得不同涉氨企业的综合评价的结果为

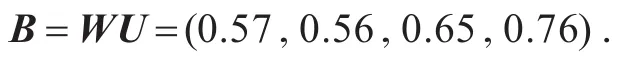
综上所述可知不同涉氨企业的综合评价的安全优劣等级为：企业Q为0.758 4处于较安全的级别，（良好）.企业O为0.647 7处于安全生产的级别（及格）.企业M和企业N分别为0.574 1、0.558 2，处于存在安全隐患的阶段，需要排除和治理隐患，进一步达到安全生产的级别.

3 结语

液氨泄漏的二级风险评价综合模型，能完全实现多属性、多样本、多目标的定性和定量指标的综合性评判.该评价模型优于其它模型.

运用该模型建立了4个一级指标，22个二级指标.系统的分析引起合成氨企业发生液氨泄漏产生的问题的主要原因是人员业务技术水平和职业素质与安全意识的高低，主要的隐患和缺陷为生产工艺系统和储罐系统，并按相互的关联研究了各个因素的危害程度，综合地评估出合成氨企业液氨泄漏的风险大小.

运用此方法可知：应加强员工的专业知识和技术水平、岗前的培训和职场的教育、企业安全文化教育专栏的设置、增加安全机构的业务能力、完善法律法规企业定性指标的检测方法形成高目标、高质量、高要求的标准，以便降低企业的泄漏风险，达到人们可接受的安全范围.

加强生产工艺系统和储罐系统的定期与不定期的检查力度、实施设备的维修及更新淘汰机制、加强人工智能化检测的建设，达到人与科技的双控防范措施，对于提高合成氨企业安全生产目标的控制、应急救援、编写应急预案的水平有着重要的作用，也为降低风险达到可接受的水平提供决策和技术指导.

［1］沈斐敏.安全系统工程理论与应用［M］.北京：北京煤炭工业出版社，2001.

［2］李刚.MATLAB函数速查手册［M］.北京：北京清华大学出版社，2011.

［3］相艳景，刘茂.液氨储罐泄漏中毒事故的个人风险分析［J］.安全与环境学报，2009（1）：176-179.

XIANG Y J，LIU M.Personal risk analysis over the ammonia poisoning accidents caused by the use of liquidammoniatanks［J］.JournalofSafetyandEnvironment，2009（1）：176-179.

［4］孟凡亭，吴欣甜，张苗，等.液氨泄漏爆炸的模糊事故树分析研究［J］.南开大学学报（自然科学版），2014（4）：14-20.

MENG F T，WU X T，ZHANG M，et al.Fuzzy tree analysis model for liquid ammonia leakage explosion［J］. Acta Scientiarum Naturalium Universitatis Nankaiensis，2014（4）：14-20.

［5］许树柏.译.SATTYTL层次分析法［M］.北京：北京煤炭工业出版社，1988.

［6］赵焕臣，许树柏，和金生.层次分析法［M］.北京：北京科学出版社，1988.

［7］邓雪，李家铭，曾浩健，等.层次分析法权重计算方法分析及其应用研究［J］.数学的实践与认识，2012（7）：93-100.

DENG X，LI J M，ZENG H J，et al.Research on computation methods of AHP wight vector and its applications［J］.Mathematics in Practice and Theory，2012（7）：93-100.

［8］阮铖巍，寇英信，徐安，等.基于二元模糊比较法的单步空战机动决策研究［J］.指挥控制与仿真，2012（5）：10-13.

RUAN C W，KOU Y X，XU A，et al.Research on single step manuvering decision in air combat based on binary Fuzzy comparison method［J］.Command Control &Simulation，2012（5）：10-13.

［9］赵峰，廖志海，乔洪波，等.二元比例X射线荧光光谱法测定铀锆体系中铀和锆［J］.冶金分析，2015（7）：44-47.

ZHAO F，LIAO Z H，QIAO H P，et al.Determination of uranium and zirconium in uranium-zirconium system by binary ratio X-ray fluorescence spectrometry［J］. Metallurgical Analysis，2015（7）：44-47.

［10］徐兵兵，张妙仙，王肖.改进的模糊层次分析法在南苕溪临安段水质评价中的应用［J］.环境科学学报，2011（9）：2066-2072.

XU B B，ZHANG M X，WANG X.Application of an improved fuzzy analytic hierarchy process in water quality evaluation of the South Tiaoxi River，Linan section［J］.Acta Scientiae Circumstantiae，2011（9）：2066-2072.

［11］张杰，赵明.液氨泄漏事故的定量风险评价研究［J］.安全与环境工程，2012（1）：69-72.

ZHANG J，ZHAO M.Study on the quantitative risk assessment of ammonia leakage accident［J］.Safety and Environmental Engineering，2012（1）：69-72.

［12］柳红卫，黄沿波.液氨泄漏风险评估和风险分级方法［J］.安全与环境工程，2010（1）：70-74.

LIU H W，HUANG Y B.Risk assessment of liquid ammonia leakage and method of risk classification［J］. Safety and Environmental Engineering，2010（1）：70-74.

［13］夏登友，钱新明，黄金印，等.液氨泄漏扩散模拟及危害评估［J］.中国安全科学学报，2014（3）：22-27.

XIA D Y，QIAN X M，HUANG J Y，et al.Diffusion simulation and hazard evaluation for liquid ammonia leakage［J］.China Safety Science Journal，2014（3）：22-27.

［14］孙莉，赵颖，曹飞，等.危险化学品泄漏扩散模型的研究现状分析与比较［J］.中国安全科学学报，2011（1）：37-42.

SUN L，ZHAO Y，CAO F，et al.Comparison and analysis on the research situation of release and dispersion models of hazardous chemicals at home and abroad［J］.China Safety Science Journal，2011（1）：37-42.

［15］王静，叶海明.液氨少量泄漏事故风险预测分析［J］.化学工程师，2013（5）：46-49.

WANG J，YE H M.Discussion on environment risk assessment of accident of small amount of liquid ammonia［J］.Chemical Engineer，2013（5）：46-49.

本文编辑：陈小平

Risk Analysis of Liquid Ammonia Leakage Based on Analytic Hierarchy Process and Fuzzy Theory

ZHOU Dehong1，WANG Haoran1，2，LI Wen1，FNEG Hao1
1.School of Resources and Civil Engineering，Wuhan Institute of Technology，Wuhan 430074，China；2.School of Computer Science and Technology，Xiantao Vocational College，Xiantao 433000，China

The hierarchical-fuzzy theory was executed in liquid ammonia enterprises for qualitative and quantitative risk assessment.The class layer structure model of accident causes was built from four aspects，the unsafe behavior of employees，the unsafe condition of equipment and facilities，safety management deficiencies and poor working environment.The affect level of incident cause was evaluated.The safety merits order and existence of leakage risk characteristics were analyzed by using the models of some ammonia enterprises.It is suggested that we should implement the corporate legal law，develop the professional knowledge and technology of staffs，improve the regular and irregular safety inspection for production process system and storage tank system，establish equipment maintenance and update mechanism，strengthen the artificial intelligence detection to realize the dual control of people and technology.

liquidammonialeakage；classstructuremodel；fuzzytheory；analytichierarchyprocessriskassessment

TD853，TD325

A

10.3969/j.issn.1674⁃2869.2017.03.013

1674-2869（2017）03-0281-07

2016-05-20

2015年安全生产重大事故防治关键技术科技项目（hubei-0008-2015AQ）；湖北省安全生产监督管理局2015年安全生产专项资金（鄂安监发［2015］73号）；湖北省安全生产监督管理局2016年安全生产专项资金（鄂安监发［2016］54号）；武汉工程大学第二批校级课程综合改革项目（校教［2016］6号）；武汉工程大学研究生教育创新基金（CX2015038）；武汉工程大学2016年研究生教育改革研究项目（yjg201601）

周德红，博士，副教授.E-mail：zhoudehongwuhan@163.com

周德红，王浩然，李文，等.基于层次分析法和模糊理论的液氨泄漏风险研究［J］.武汉工程大学学报，2017，39（3）：281-287. ZHOU D H，WANG H R，LI W，et al.Risk analysis of liquid ammonia leakage based on analytic hierarchy process and fuzzy theory［J］.Journal of Wuhan Institute of Technology，2017，39（3）：281-287.