一种月表采样器合理铲挖深度的研究

2017-07-18姚猛郑燕红赵志晖金晟毅司永顺韩璐

航天器工程 2017年3期

关键词：采样器月面月壤

姚猛郑燕红赵志晖金晟毅司永顺韩璐

(北京空间飞行器总体设计部，北京 100094)

一种月表采样器合理铲挖深度的研究

姚猛郑燕红赵志晖金晟毅司永顺韩璐

(北京空间飞行器总体设计部，北京 100094)

铲挖深度是月表采样器的重要技术指标，合理的铲挖深度需既能降低采样器安全风险又可确保一定的采样效率。设计了一种斜插式铲挖方法的月表采样器，针对其构型与铲挖方法,在Reece模型的基础上，通过离散元法推导了月表采样器铲挖阻力矩的表达式。参考历次阿波罗飞船(Apollo)月壤样本数据，在实验室环境下构筑了与月壤物理特性相匹配的模拟月壤，并测得模拟月壤的物理特性参数。然后，根据所测得模拟月壤的物理特性参数，利用所推导的铲挖阻力矩表达式，对月表采样器典型输出力矩下的铲挖深度进行了仿真分析与试验验证，仿真分析结果与试验结果吻合。根据试验结果与月表采样器设计参数确定了合理的铲挖深度，可为月表采样器在月面采样时提供参考。

采样器；铲挖阻力矩；仿真与验证；铲挖深度

1 引言

目前，我国正在开展探月三期工程，其主要任务是实现月面采样及返回[1]。为实现月面采样，机械臂携带采样器在月面进行多点多次采样。采样器铲挖深度将会对采样效率与安全性产生直接影响，铲挖深度较浅时会降低单次采样量，从而增加采样次数与月面工作时间；而铲挖深度较深时，采样器的驱动力矩可能无法满足铲挖阻力矩要求导致采样器卡滞在月壤中，当采样器卡滞在月壤中时，采样器会发生堵转进而可能烧毁电机，对采样器造成较大的安全风险。因此，在月面有限的采样时间内，在确保安全风险的基础上，为提高采样效率，需根据采样器特性确定合理的铲挖深度。

铲挖深度是铲挖阻力的直观表现形式，而影响铲挖阻力的主要因素包括月壤重力、月壤力学特性(密度、内聚力、内摩擦角、月壤与采样器摩擦角等)、采样器结构等[2-4]。国内外学者对铲挖阻力进行了大量的研究，Mckyes模型和Reece模型针对二维推土板与土壤的切割过程，给出了不同的铲挖阻力表达式[5-6]。Mckyes模型提出了铲挖阻力由推移阻力、粘着力、铲挖惯性力组成；Reece模型提出了铲挖阻力由推移阻力、粘着力、附件月壤阻力构成。李操在Mohr-Coulomb屈服准则和Rankine理论的基础上建立了月壤-铲斗挖掘模型，通过离散元法推导了主/被动土压力的数学表达式，给出了主/被动土压力与月壤特性的函数关系[7]。安明国开展了不同土壤的挖掘试验，根据所观察到的土壤破坏机理，结合工程经验，建立了挖掘阻力的基本方程[8-9]。

上述研究工作主要侧重于建立与优化铲挖阻力模型，提出了不同的铲挖阻力模型，但对铲挖阻力的实际应用研究较少。本文在分析采样器铲挖机理的基础上，结合采样器构型，利用Reece模型和离散元法对铲挖深度进行了分析，并开展了验证试验，确定了合理的铲挖深度，使采样器在月面采样时既能确保安全又可确保一定的采样效率，可为采样器月面采样提供参考。

2 采样器设计

2.1 构型设计

月表采样器采用斜插式铲挖方法，如图1所示，其原理简单，结构紧凑，可靠性高。采样器安装在机械臂上，在月面开展采样时，由安装在探测器上的机械臂将采样器转移至月面，实现采样。

图1 采样器示意图Fig.1 Schematic diagram of sampler

采样器的采样执行部分为摇臂铲，由直流电机与减速器进行驱动，直流电机通过减速器驱动摇臂铲转动进而实现月壤的铲挖。摇臂铲的输出力矩与电机的输入电流成正比。采样器摇臂铲结构采用曲面式设计，既可增加内部容积又便于月壤在内部自然滑动。摇臂铲分为切削板和推移板，如图2 所示，分别用于切削月壤和推移月壤，两者采用一体化设计与加工。

图2 摇臂铲示意图Fig.2 Schematic diagram of rotating shovel

2.2 铲挖过程

采样器铲挖过程主要分为4部分，如图3所示。铲挖月壤前，摇臂铲打开至一定角度；在铲挖初期，切削板用于切削月壤，以便能够顺利插入月壤；待切削板完全插入月壤后，推移板与月壤接触，推移板推移待铲挖月壤，经而实现月壤的铲挖。

为简化铲挖模型，将推移板曲面结构简化为平面结构，如图4所示。图4中，L为推移板长度，D为最大铲挖深度，(L-D)为推移板露出月壤部分的高度，H为推移板底部深度，h为变量，其定义为待铲挖月壤中任意一点的深度，Ψ为铲挖角度，α为铲挖月壤时推移板旋转角度的半角。

在铲挖月壤时，采样器处于确定的高度位置(L-D)，因此推移板的铲挖面为扇形区域。由于推移板长度L已知，当摇臂铲高度位置(L-D)确定后，在几何上的铲挖深度D也随之确定；当推移板旋转至与重力线夹角为Ψ(铲挖角度，范围为[-α,α])时，推移板底部深度为H。

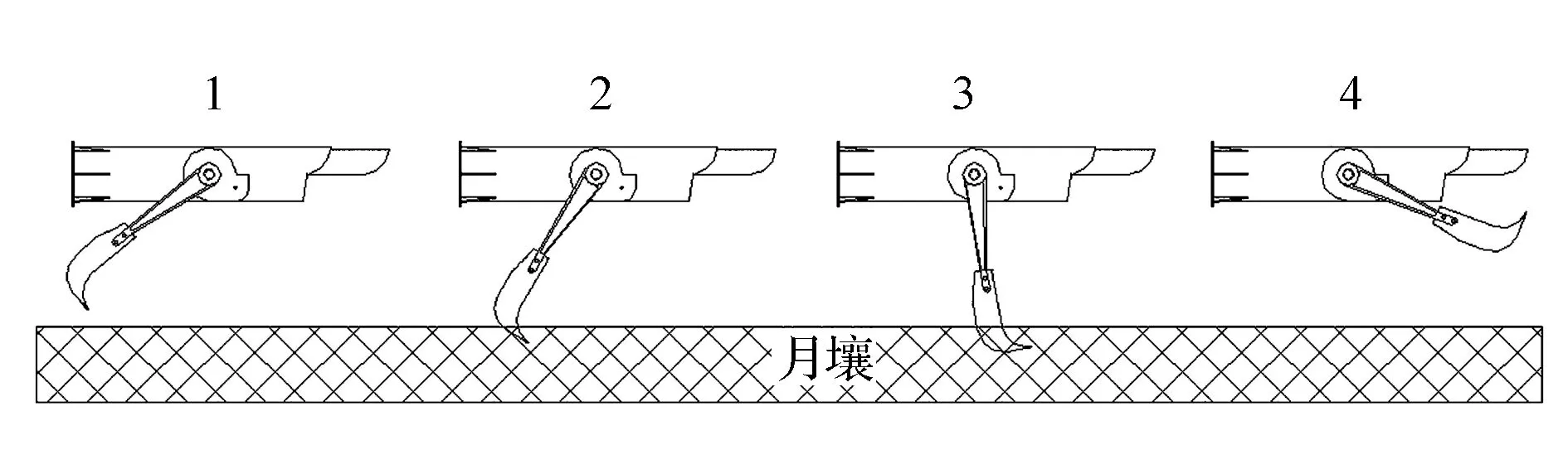
图3 铲挖过程示意图Fig.3 Schematic diagram of excavating process

图4 铲挖模型几何图Fig.4 Geometrical diagram of excavating model

3 铲挖阻力模型

3.1 铲挖阻力分析

采样器的铲挖阻力主要包括：推移阻力、月壤内聚力、堆积月壤的附加阻力、月壤与摇臂铲铲斗底部及侧面的摩擦力、惯性力等。在建立挖掘阻力模型时需尽可能考虑较多的影响因素，但过于追求模型的完整性会导致计算式冗长，计算量较大，甚至无法计算。因此，基于Reece模型，本文仅考虑推移阻力、月壤内聚力和堆积月壤的附加阻力，忽略月壤与摇臂铲外侧的摩擦力；同时由于摇臂铲在铲挖过程中运动速度较慢，忽略惯性力。

摇臂铲在铲挖月壤过程中，受力形式如图5所示，θ为待铲挖月壤滑移面与水平面夹角，并假设δ为推移板与月壤间的摩擦角，φ为月壤间内摩擦角。

图5 推移阻力模型图Fig.5 Diagram of pushing resistance model

1)月壤推移阻力

Fp=γbh2·

(1)

式中：γ为月壤重度值(N/m3)；b为摇臂铲铲斗宽度。

2)堆积月壤阻力[3]

Fq=GqNq=γbSΔNq

(2)

式中：Gq为堆积月壤的重力；Nq为堆积月壤阻力的影响系数；SΔ为已挖掘月壤的截面积。

Nq=

(3)

3)待铲挖月壤粘着阻力[7]

Fc=chNc

(4)

式中：c为月壤内聚力;Nc为月壤粘着阻力影响系数。

(5)

3.2 采样器所受铲挖阻力矩

1)推移阻力矩Mp

利用离散元法，对图5中月壤进行离散化处理，结合图4中采样器铲挖几何模型，离散后月壤层推移阻力对摇臂铲形成的阻力矩为

(6)

积分后整理可得

(7)

2)堆积月壤阻力矩Mq

结合式(3)中堆积月壤阻力表达式与图4中采样器铲挖几何模型，堆积月壤对摇臂铲所产生的阻力矩为

(8)

3)粘着阻力矩Mc

由式(5)可知，月壤粘着阻力是铲挖深度的函数，利用离散元法，对图5中月壤进行离散化处理，结合图4中采样器铲挖几何模型，月壤粘着阻力对摇臂铲所产生的阻力矩为

(9)

将式(5)与式(6)代入式(10)，积分后可得

(10)

4)摇臂铲所受铲挖阻力矩M

由上述分析可知，待铲挖月壤对摇臂铲的铲挖阻力矩为

M=Mp+Mq+Mc

(11)

将式(7)、(8)、(10)代入式(11)后即可求得铲挖阻力矩的表达式。

4 仿真分析与试验验证

4.1 月壤参数

由式(7)、(8)、(10)可知，影响挖掘效果的月壤参数主要包括月壤重度、月壤内摩擦角、月壤-摇臂铲摩擦角、内聚力。参考历次阿波罗飞船(Apollo)月壤样本，在实验室环境下构筑了与月壤物理特性相匹配的模拟月壤[10]。通过地面试验，测得模拟月壤主要物理特性如表1所示。

表1 模拟月壤物理参数

4.2 仿真分析

由式(7)、(8)、(10)可知，推移阻力矩、堆积月壤阻力矩、粘着阻力矩均与铲挖角度Ψ、采样器高度位置(L-D)相关。在铲挖月壤时，采样器高度位置(L-D)保持不变，且当月壤物理参数确定时，在整个铲挖过程中，铲挖阻力矩仅与铲挖角度Ψ有关，即

M=Mp+Mq+Mc=f(Ψ)

(12)

绘制铲挖阻力矩M和铲挖角度Ψ的函数关系曲线图，如图6所示。通过对式(12)中函数求极值方式，求得当Ψ=-27.7°(-0.483 9 rad)时，铲挖阻力矩最大。

图6 铲挖阻力矩与铲挖角度关系曲线图Fig.6 Relationship curve of excavation resistance torque with excavation angle

由图4可知，挖掘角度Ψ与摇臂铲长度L、铲挖深度D、摇臂铲瞬时铲挖深度H的关系有

(13)

联立式(12)、(13)，理论上可求得在摇臂铲输出力矩下的铲挖深度。但由于式(12)较为复杂，难以直接求解。将式(13)代入式(12)后利用曲线交汇的方式求解铲挖深度D。将式(12)分解为如下函数。

(14)

式中：f1(D)为铲挖阻力矩与推移阻力矩之差与铲挖深度的函数关系；f2(D)为月壤附加阻力矩与粘着阻力矩之和与铲挖深度的函数关系。

通过绘制两条函数曲线，曲线的交点即为式(12)、(13)的数值解。由于摇臂铲铲挖月壤时，速度均匀且缓慢，因此可将摇臂铲输出力矩等效为月壤阻力矩，即可求得在摇臂铲输出力矩下的铲挖深度。以摇臂铲输出力矩为8.4Nm为例，月壤物理参数按表1取值，铲挖角度Ψ=-27.7°，两条曲线绘制结果如图7所示，两条曲线相交时，铲挖深度为6.11 cm。

采样器电机最大输入电流为0.3 A，对应的最大输出力矩为8.4 Nm，且输入电流与输出力矩成正比。根据上述求解方法，对典型输出力矩状态下的铲挖深度进行了求解，结果如表2所示。

图7 铲挖深度分析结果Fig.7 Simulation results of excavation depth

表2 典型输出力矩状态下的铲挖深度分析结果

根据表2中的计算结果绘制对应曲线，如图8所示，摇臂铲输出力矩与铲挖深度呈近似线性关系。

图8 典型输出力矩下的铲挖深度曲线图Fig.8 Excavation depth curve for typical output torque

4.3 试验验证

为验证分析结果的有效性，设计了采样器铲挖试验。试验中模拟月壤参数与表1中参数一致。摇臂铲为试验样机，通过设置采样器电机输入电流，控制其输出力矩。在典型输出力矩状态下测量铲挖深度，实物图如图9所示，试验结果如表3所示。

图9 采样器铲挖深度试验实物图Fig.9 Test of excavation depth of the sampler

表3 典型输出力矩状态下的铲挖深度实测结果

图10 铲挖深度分析结果与试验结果对比图Fig.10 Comparison curve of excavation depth about simulation results and testing results

如图10所示，将分析结果和试验结果进行对比可发现：分析结果与试验结果基本吻合，在同一输出力矩状态下，铲挖深度的试验结果比仿真分析结果略小，实际铲挖深度较仿真分析结果略浅。这是因为在实际铲挖过程中，存在摇臂铲外侧与月壤间的摩擦力和铲挖过程中的惯性力，但摇臂铲外侧与月壤间的摩擦力较小，且摇臂铲在铲挖过程中运动速度较慢，为简化计算，在仿真分析过程中将二者忽略处理了。

5 合理铲挖深度的确定

合理的铲挖深度需既能确保采样器安全，又能确保一定的采样量。在月面采样时，铲挖深度越深，采样量越多，效率越高，但也会存在采样深度较深导致采样器摇臂铲卡滞在月壤中的风险，从而因堵转烧毁电机；如采样深度较浅，虽能确保采样器摇臂铲不会卡滞在月壤中，但会因采样量较少而增加采样次数，从而增加月面采样工作时间，降低月面工作效率；为此需确定合理的铲挖深度。

对于合理的铲挖深度，可根据探测器中运动部件静力矩裕度不小于1的准则进行确定，运动部件的静力矩裕度计算公式为

ηs=Fm/Fr-1

(15)

式中：ηs为运动部件的静力矩裕度；Fm为驱动力矩；Fr为静态阻力矩。

由于采样器电机最大输入电流为0.3 A，对应的摇臂铲最大输出力矩即驱动力矩为8.4 Nm，在静力矩裕度设定为1的情况下，将驱动力矩8.4 Nm代入(15)中后可计算出静态阻力矩为4.2 Nm，此时，静态阻力矩即为铲挖阻力矩。由表3可以看出，当采样器输入电流为0.15 A时，采样器输出力矩为4.2 Nm，刚好能够克服铲挖阻力矩完成采样，此时铲挖深度为3.1 cm。因此，取整后将3 cm设定为合理的铲挖深度，在此铲挖深度下，采样器的输出力矩仍有一倍的安全余量，确保摇臂铲不会卡滞在月壤中。

在理想状态下，当采样器铲挖深度为3 cm时，既能确保采样器安全又能确保一定的采样量，但在工程实践中考虑到机械臂的定位精度误差(在月面开展采样时，由安装在探测器上的机械臂将采样器转移至月面，实现采样)，在每次采样时，难以按预定的铲挖深度进行精准铲挖，因此，合理的铲挖深度应为一个范围值，即范围上限为3 cm；而对于下限值，本文所设计的机械臂样机定位精度指标为±5 mm，则下限值为2 cm。由表3可以看出，当铲挖深度为2.3 cm时，采样量约为89 g，而采样量与铲挖深度大致呈线性关系，根据线性计算，当铲挖深度为2 cm时，采样量约为77 g左右，能够确保一定的采样量。

综上所述，在本文所设计的采样器与机械臂相关指标条件下，合理的铲挖深度范围应为2～3 cm。

6 结论

(1)经仿真分析与试验验证，在Reece模型的基础上，结合采样器采样构型与铲挖方法，利用离散元法推导的采样器铲挖阻力矩表达式有效。

(2)由于未考虑摇臂铲外侧与月壤间的摩擦力以及铲挖过程中的惯性力，导致铲挖深度的试验结果较分析结果略小，后续有待做进一步研究。

(3)根据所设计的采样器与机械臂相关指标，合理的铲挖深度应为2～3 cm，在此范围内既可确保采样器安全又可确保采样效率，同时也能够确保在工程实践中的可实现性。

References)

[1]李操，谢宗武，李永绍，等. 一种应用于月球样品采集、返回计划的末端执行器[J]. 机器人，2013,35(1)：9-17

Li Cao,Xie Zongwu,Li Yongshao,et al. A novel end-effector for lunar sample acquisiton and return[J]. Robot,2013,35(1):9-17 (in Chinese)

[2]梁磊，魏承，赵阳. 浅表层月壤铲挖采样的振动减阻技术仿真研究[J]. 航天器环境工程,2013,30(3):256-261

Liang Lei,Wei Cheng,Zhao Yang. Simulation of vibration drag-reduction in the excavation sampling of lunar regolith[J]. Spacecraft Environment Engineering,2013,30(3):256-261 (in Chinese)

[3]段隆臣,李谦,张大伟,等. 基于模拟月壤的表层采样试验研究[J]. 探矿工程(岩土钻掘工程),2014,41(1):3-8

Duan Longchen,Li Qian,Zhang Dawei,et al. Experimental research on surface sampling based on lunar soil simulants[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling),2014,41(1):3-8 (in Chinese)

[4]高辉,段隆臣,李谦,等. 模拟月壤表层采样试验研究[J]. 地质科技情报，2014,33(6):175-178

Gao Hui,Duan Longchen,Li Qian，et al. Surface sampling experiment for lunar soil simulant[J]. Geological Science and Technology Information,2014,33(6):175-178

[5]Mckyes E. Soil cutting and tillage[M]. Amsterdam:Elsevier,1985

[6]Reece A. The fundamental equation of earth-moving mechanics[J]. Proceedings of the Institution of Mechanical Engineers,1964(1):16-22

[7]李操. 基于机械臂的月壤挖掘采样及力学参数辨识的研究[D]. 哈尔滨:哈尔滨工业大学,2014

Li Cao. Study of lunar soil excavation acquisition and mechanical parameters identification based on robot arm[D]. Harbin:Harbin Institute of Technology,2014 (in Chinese)

[8]安国明. 反铲斗挖掘土壤实验研究与挖掘阻力计算(上)[J]. 建筑机械化，2005(4)：26-28

An Guoming. Experimental research about backhoe excavating soil calculating the excavating resistance(1)[J]. Construction Mechanization,2005(4):26-28 (in Chinese)

[9]安国明. 反铲斗挖掘土壤实验研究与挖掘阻力计算(下)[J]. 建筑机械化，2005(5)：34-39

An Guoming. Experimental research about backhoe excavating soil calculating the excavating resistance(2)[J]. Construction Mechanization,2005(5):34-39 (in Chinese)

[10]欧阳自远. 月球科学概论[M]. 北京：中国宇航出版社，2005

Ouyang Ziyuan. Introduction to lunar science[M]. Beijing：China Astronautic Press，2005

(编辑：张小琳)

Research on Reasonable Excavation Depth for Lunar Regolith Sampler

YAO Meng ZHENG Yanhong ZHAO Zhihui JIN Shengyi SI Yongshun HAN Lu

(Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

Excavation depth is an important parameter of lunar regolith sampler. The reasonable excavation depth can not only reduce the safety risk of lunar regolith sampler but also ensure certain excavation efficiency. A kind method of lunar regolith sampler is designed which excavates lunar soil by the way of oblique breaking in. For the configuration and excavation way of the lunar regolith sampler,an equation of excavation resistance torque is derived through discrete element method based on Reece model. Simulated lunar soil is constructed in the laboratory environment referring to the sample data of Apollo and the physical parameters of the simulated lunar soil is measured. The excavation depth of sampler’s typical output torque are emulated and tested based on the parameters of the simulated lunar soil and the equation of excavation resistance torque. The emulation results and testing results are coincident. The reasonable excavation depth is proposed based on testing results and the designed parameters of the lunar regolith sampler. The reasonable excavation depth provides reference for lunar regolith excavation of the lunar regolith sampler.

sampler；torque of excavation resistance；emulation and testing；excavation depth