火炮后坐阻力的区间不确定性优化研究

李 荣,杨国来,孙全兆,萧 辉

(南京理工大学 机械工程学院,江苏 南京 210094)

火炮后坐阻力的区间不确定性优化研究

李 荣,杨国来,孙全兆,萧 辉

(南京理工大学 机械工程学院,江苏 南京 210094)

为减小火炮炮架受力,获得更优后坐阻力规律,进行了后坐流液孔尺寸的区间不确定性优化研究。结合公差带定义了三参数区间,构建了基于三参数区间的不确定性优化模型及算法;以流液孔的几何尺寸为不确定性变量,利用上述方法对节制杆形状尺寸进行了区间优化设计;优化求解了不同公差等级的节制杆外径。研究结果表明:优化后的后坐阻力峰值区间更小,后坐阻力曲线更加平缓,充满度更好。实现了节制杆外径尺寸设计与公差设计的同步优化,得到了兼顾工艺性和后坐阻力的节制杆外径设计方案。

火炮;后坐阻力;结构设计;区间优化;尺寸不确定性

通过设计火炮反后坐装置的制退机液压阻力可得到后坐阻力的规律,它极大地减小了火炮炮架受力。典型节制杆式制退机的液压阻力是靠制退机活塞挤压液体高速流过流液孔而产生,故后坐阻力规律实际是由流液孔面积的改变实现的[1]。宗士增[2]考虑了火炮后坐和全炮运动的相互影响,建立了火炮反后坐装置动力学耦合模型,以节制杆尺寸为设计变量进行了结构优化。周成[3]以后坐阻力曲线与拟定的后坐力曲线的符合程度、后坐长与设计值的接近程度为目标函数,建立以节制杆尺寸为设计变量的优化模型。这些文献所建立的模型都是确定性的模型,即认为材料特性、载荷、几何尺寸等参数在优化过程中不存在摄动,忽略了参数的不确定性对目标性能的影响[4]。然而,加工和装配得到的流液孔尺寸是不确定的,它会影响火炮的后坐阻力和后坐长,因此需要研究流液孔尺寸的不确定性。

区间优化方法仅需知道不确定性变量的上下限,因此,采用区间优化理论及算法来研究不确定性问题[5]。Jiang C[6]定义了公差指标,通过基于可靠度的区间可能度模型,提出了考虑公差的区间优化方法,同时优化得到了名义尺寸和公差。谢慧超[7]基于区间分析方法,建立了一种汽车悬架平顺性的不确定性优化模型,在保证平顺性的前提下使设计参数的对称公差最大化。上述区间优化方法采用区间中点和半径的形式来表征既是区间变量又是设计变量的量,但在机械工程实际中,尺寸常采用公差带来表征,区间中点和半径的形式使得优化结果难以应用。

针对火炮炮架受力大的问题,从后坐流液孔几何尺寸偏差的角度进行了区间优化研究。先结合公差带定义了三参数区间,建立了三参数区间的不确定性优化模型及算法;然后以节制杆各段折点直径、节制环内径、制退杆活塞与制退筒的间隙和节制环与节制杆起始位置的轴向装配误差作为不确定性变量,采用上述优化方法进行了后坐阻力的优化,并定量评估了后坐阻力曲线的充满度和平缓度。

1 三参数区间的不确定性优化

1.1 三参数区间定义

考虑结构尺寸由加工和测量引起的不确定性,合格产品的尺寸会在设计的公差带范围内摄动。公差带是上极限尺寸和下极限尺寸所限定的一个范围,它的数学本质是区间。公差带一般有3种形式,区间一般有2种形式,如表1,表中Dmin为下极限尺寸,Dmax为上极限尺寸,D为公称尺寸,es为上极限偏差,ei为下极限偏差,ITn为公差等级,xL为区间下限,xR为区间上限,xC为区间中点,xC=(xL+xR)/2,xW为区间半径,xW=(xR-xL)/2。

表1 公差带和区间的形式及示例

公称尺寸是选型的标准,而且确定性设计方法是以公称尺寸为基础;公差可表示加工的精度,还影响着零部件的成本。因此,机械工作者关心的尺寸参数是公称尺寸和公差。表1中公差带的后2种形式均包含3个参数,同时能有效地表示上述2个特征,然而现有两参数的区间形式均不符合设计要求,其中区间中点和半径的形式只是表1中公差带第2种形式的特例。区间形式限制了区间优化方法对不确定性结构尺寸的研究。

由于公差大小不仅与公差等级相关,还与公称尺寸的大小相关,同时还是离散的,本文以公称尺寸和公差等级为基础构造三参数区间。

综上,三参数区间记为

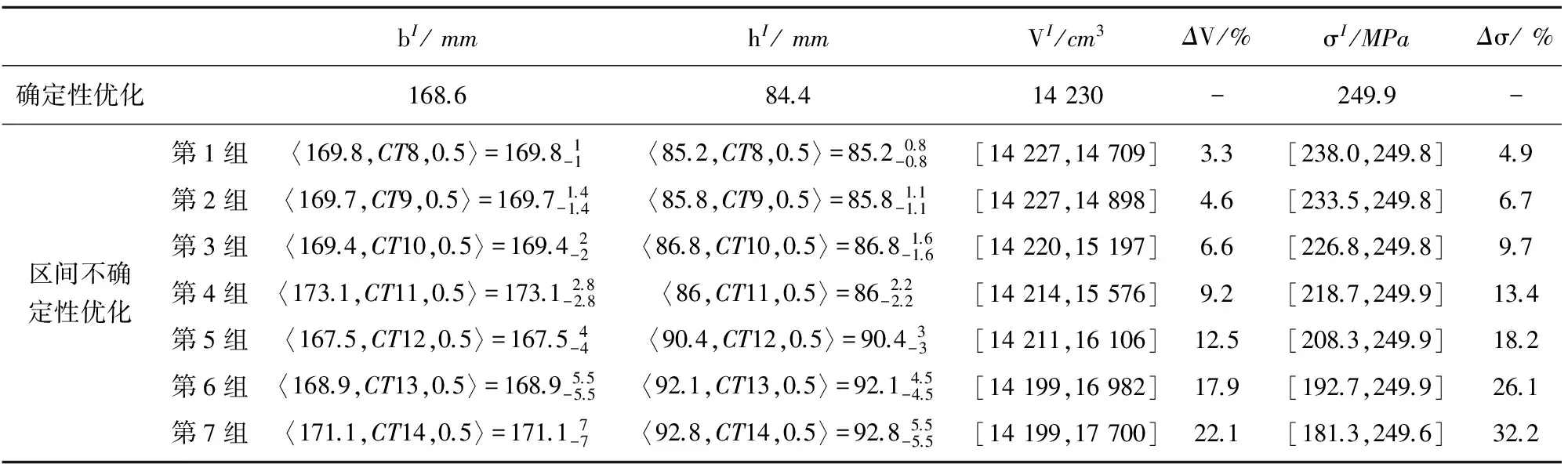
xI=〈xg,xIT n,xθ〉={x|xg-xθxt

xt,x、xg、xθ∈R}

(1)

1.2 三参数区间不确定性优化模型及算法

1.2.1 三参数区间设计变量转化

区间优化理论建立在两参数的区间变量基础上,故需将三参数区间转化为两参数区间。一般公差带的实际约束如下:

①公差等级要求。以光轴为例,规定光轴的外圆公差等级为ITn,即xIT n为常数。

②行业习惯。如在铸造生产中,行业习惯标注对称公差,即xθ=0.5。

因此,三参数区间设计变量可通过公差带实际等式约束h(x)=0转化为两参数区间。

1.2.2 目标函数和约束函数的确定性转化

采用罚函数将目标和约束区间处理为增广目标区间,那么目标和约束函数的确定性转化的实质是增广目标区间的排序。先采用姜潮[4]提出的区间可能度模型进行区间的两两比较,然后建立可能度矩阵,并用徐泽水[8]提出的排序公式进行排序。区间可能度定量描述了一区间优于另一区间的具体程度,模型如下:

(2)

式中:AI和BI为区间,AR和AL分别为区间AI的上、下限,BR和BL分别为区间BI的上、下限。

(3)

1.2.3 三参数区间不确定性优化模型

通过上述确定性转化,一般的优化模型可转化为如下三参数区间不确定性优化模型:

(4)

式中:f为目标函数,X为设计向量,m为设计变量的个数,g(XI)为不等式约束函数。

1.2.4 算法流程

上述不确定性优化问题的求解一般是两层嵌套优化问题,其中外层用于设计向量的寻优,内层用于计算不确定目标和约束区间。本文外层采用NSGA-Ⅱ遗传算法,为兼顾计算效率和精度,在不确定程度较小的情况下,内层采用对称拉丁超立方试验设计方法(SLHS)[9]计算目标和约束区间,内层不再需不断寻优,因此两层嵌套优化问题被解耦为单层优化问题,算法流程如图2所示。

1.3 悬臂梁算例

如图3所示矩形截面悬臂梁结构[6],长度L=1 000mm,截面尺寸为b和h,顶端受水平载荷Fx=50kN和垂直向下载荷Fy=25kN的作用。

悬臂梁最大应力σ在固定端,计算公式为

(5)

以截面尺寸b和h为设计变量,σ满足许用应力[σ]=250 MPa的约束,以体积V最小为优化目标,建立确定性优化模型。

考虑铸造悬臂梁的制造误差,有3个不确定变量b、h和L,三者公差等级相同,均采用铸造公差标准(GB/T6414-1999),且根据铸造行业习惯,无特殊要求的尺寸均用对称公差形式。采用三参数区间不确定性优化方法建立优化模型:

(6)

根据砂型铸造大批量生产达到的公差等级范围,悬臂梁铸造公差等级选定CT8、CT9、CT10、CT11、CT12、CT13和CT14分别进行优化求解,并采用遗传算法进行确定性优化,尺寸圆整后的结果均列入表2。表中,ΔV为悬臂梁体积摄动百分率,σI为悬臂梁固定端应力,Δσ为悬臂梁固定端应力摄动百分率。

表2 确定性优化结果和区间不确定性优化结果对比

从表2可知,随着公差等级的增大,悬臂梁体积和固定端应力的摄动也在增大,最大分别达到22.1%和32.2%,表明尺寸的不确定性在设计时必须加以考虑。与确定性优化结果对比,不确定性优化值偏大,因为它考虑了结构尺寸的摄动对悬臂梁体积和应力的影响,具有更好的稳健性。体积最小为轻量化要求,公差等级与制造工艺性相关。如果设计者对悬臂梁质量较关注,可以选择第1组和第2组数据;如果对工艺性较关注,可以选择第6组和第7组这两组;如果需综合考虑质量和工艺性,则可选择第3组、第4组和第5组这三组方案。

悬臂梁算例表明,三参数区间的不确定性优化联合了结构尺寸设计与公差设计,得到了截面尺寸及其公差带,并得到稳健性更好的设计方案。

2 基于三参数区间的后坐阻力优化

2.1 火炮后坐受力分析

火炮射击时,其受力十分复杂,取后坐部分为研究对象,在后坐过程中,主动力Fpt是火炮发射时产生后坐运动的原因,而后坐阻力FR是阻止后坐运动的原因。后坐阻力包括制退机的液压阻力Fh、复进机力Ff和它们紧塞装置的摩擦力F、摇架导轨摩擦力FT、后坐部分重力沿炮膛轴线分力mhgsinφ。则后坐运动微分方程为

(7)

2.2 后坐反面问题计算模型验证与分析

加工和装配是流液孔几何尺寸产生不确定性的重要原因。以节制杆各段折点直径dk、节制环内径dp、制退杆活塞与制退筒间隙Δδ1、节制环与节制杆起始位置的轴向装配误差Δl作为不确定性变量,其中前两者主要由加工引起,后两者主要由装配导致。典型节制杆式制退机结构如图4所示。

以某火炮为例,在保持火炮系统基本参数和反后坐装置其他结构尺寸不变的基础上,流液孔尺寸的不确定性变量范围采用该火炮的设计参数,如表3所示。

表3 流液孔尺寸的不确定参数范围

以不确定性变量的公称尺寸为初始值,Δδ1=0.315mm为初始值,Δl=0为初始值,运用对称拉丁超立方试验设计方法在总体中抽500个样本。对每个样本,用式(7)建立的后坐运动微分方程在正常射击条件下进行后坐反面问题仿真。得到后坐阻力峰值FRmax的初始值、最小值和最大值分别为190 982N,182 391N和197 072N,后坐阻力峰值区间相对其初始值的变化率为7.69%,得到后坐长λ的初始值、最小值和最大值分别为865.8mm、853.2mm和889.3mm,后坐长λ的最小值和最大值相差36.1mm。

该火炮设计后坐长为910mm,后坐长λ的仿真值中最大为889.3mm,其与设计值的相对误差仅为2.27%,说明了仿真模型的可信性。

计算结果表明,计及流液孔尺寸不确定性,后坐阻力峰值波动为7.69%,后坐长波动为36.1mm。在传统的确定性后坐阻力优化中没有考虑流液孔尺寸的不确定性带来的目标和约束的摄动,这会导致优化结果鲁棒性差。同时传统优化不能将结构尺寸设计与公差设计联合求解。因此,需进行计及流液孔尺寸不确定性的区间优化研究。

2.3 计及流液孔尺寸不确定性的后坐阻力优化

本文通过对节制杆形状进行优化来调整流液孔面积变化规律,从而实现后坐阻力的优化。

本文在后坐长基本不变的情况下减小后坐阻力峰值,根据2.2节后坐长计算结果,故将后坐长λ约束在λ0=895mm内。同时为避免节制杆根部与节制环卡滞,节制杆与节制环配合间隙不小于Δδ2。

在第1节的基础上,建立基于三参数区间的流液孔尺寸不确定的后坐阻力优化模型:

(8)

式中:dk,min和dk,max分别为节制杆各段折点初始公称直径的最小值和最大值,λI为考虑流液孔尺寸不确定后得到的后坐长区间。

2.4 后坐阻力曲线评估

后坐阻力不仅要求其峰值小,还要求后坐阻力随后坐行程变化的曲线(FR-s)充满度好和更加平缓。目前在后坐阻力曲线的评价上,后坐阻力峰值采用定量评估,但是只有定性分析充满度和平缓度,没有建立定量的评价指标。

1)充满度。

后坐阻力FR在后坐长度λ内所做的总负功等于炮膛合力对后坐部分的总功,因此理想上的后坐阻力为常数FRC。如图6所示,充满度指阴影面积充满FRC-s直线作功面积的程度。

充满度α计算公式为

α=Sy/S

(9)

式中:Sy为设计的FR-s曲线和s轴所围成的图形与

FRC-s直线和s轴所围图形的交集所对应的面积,即阴影面积;S为FRC-s直线形成的矩形面积。

充满度α∈(0,1),α越接近1代表FR-s曲线的充满度越好,也越接近理想后坐阻力。

2)平缓度。

后坐阻力的变化越平缓越好,它有利于全炮受力和减小振动,因此平缓度是评价后坐阻力的另一重要指标。在FR-s曲线中,平缓度指后坐阻力随后坐行程变化的快慢程度,它是对整条曲线全局的描述;而导数正是反映函数因变量随自变量变化的快慢程度,但导数是函数的局部性质。因此本文采用导数的平均值来描述FR-s曲线的平缓度β:

(10)

式中:q为在整个后坐行程上等距且连续的取点个数;kw为上述第w个取点在FR-s曲线的导数。β越小,FR-s曲线的平缓度越好。

2.5 结果及分析

节制杆外径公差等级保持IT10不变,采用1.2.4节算法求解计及流液孔尺寸不确定的后坐阻力优化模型,优化前后的不确定性变量取公称值对应的FR-s曲线,如图7所示。继续取节制杆外径公差等级为IT8、IT9、IT11和IT12进行数值计算,结果圆整后计算得到后坐阻力与后坐长,如表4所示。

表4 节制杆外径取不同公差等级的优化结果

结果表明,优化后的后坐阻力峰值区间较优化前有较大幅度降低,后坐阻力曲线更加平缓,充满度更好,后坐长基本不变,而后坐阻力得到了优化,还实现了节制杆外径尺寸设计与公差设计的同步优化,使考虑设计方案的工艺性变得可行。

节制杆属于多锥度细长杆,加工过程中由于它刚性差和多锥度变截面的问题,导致加工高质量的节制杆不易,因此节制杆的工艺性需重点考虑。5个优化方案中,从工艺性角度考虑,以公差等级越大工艺性越好为准则;从后坐阻力的角度考虑,以后坐阻力峰值区间越小后坐阻力越好为准则。当设计者较为关注后坐阻力时,可选择节制杆公差等级为IT8的优化设计方案;当设计者较为关注加工工艺性时,可选择公差等级为IT11或IT12的优化设计方案;设计者需综合考虑工艺性和后坐阻力时,可选择节制杆公差等级为IT9或IT10的优化设计方案。

3 结束语

本文提出了一种三参数区间的不确定性优化模型及算法,定义了三参数区间来描述结构尺寸的不确定性,研究了三参数区间的转化,采用NSGA-Ⅱ和试验设计方法相结合的算法,将两层嵌套优化解耦为单层优化来求解。悬臂梁算例结果表明,该方法将结构尺寸优化设计与公差设计相结合,得到了关键尺寸及公差带,并能得到稳健性更好的设计方案。

利用上述提出的方法进行了计及流液孔尺寸不确定的后坐阻力优化,并对后坐阻力曲线的2个定性评价指标充满度和平缓度进行了定量化表征。结果表明,优化后的后坐阻力峰值区间较优化前有较大幅度降低,后坐阻力曲线更加平缓,充满度更好。实现了节制杆外径尺寸设计与公差设计的同步优化,得到了兼顾制造和性能的设计方案。

[1] 高树滋,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995. GAO Shu-zi,CHEN Yun-sheng,ZHANG Yue-lin,et al.Design of recoil system for gun[M].Beijing:Ordnance Industry Press,1995.(in Chinese)

[2] 宗士增,钱林方,徐亚栋.火炮反后坐装置动力学耦合分析与优化[J].兵工学报,2007,28(3):272-275. ZONG Shi-zeng,QIAN Lin-fang,XU Ya-dong.Dynamic coupling analysis and optimization of gun recoil mechamism[J].Acta Armamentarii,2007,28(3):272-275.(in Chinese)

[3] 周成,顾克秋,邵跃林.火炮制退机节制杆优化设计[J].火炮发射与控制学报,2012(4):68-70. ZHOU Cheng,GU Ke-qiu,SHAO Yue-lin.Optimal design of throttling bar in gun recoil mechanism[J].Journal of Gun Launch & Control,2012(4):68-70.(in Chinese)

[4] 姜潮.基于区间的不确定性优化理论与算法[D].长沙:湖南大学,2008:15-18. JIANG Chao.Theories and algorithms of uncertain optimization based on interval[D].Changsha:Hunan University,2008:15-18.(in Chinese)

[5] 李荣,杨国来,刘宁,等.火炮制退机关键结构尺寸及公差优化研究[J].弹道学报,2016,28(4):80-85. LI Rong,YANG Guo-lai,LIU Ning,et al.Research on optimization for key structure dimension of gun recoil mechanism considering tolerance[J].Journal of Ballistics,2016,28(4):80-85.(in Chinese)

[6] JIANG C,XIE H C,ZHANG Z G,et al.A new interval optimization method considering tolerance design[J].Engineering Optimization,2015,47(12):1 637-1 650.

[7] 谢慧超,姜潮,张智罡,等.基于区间分析的汽车平顺性优化[J].汽车工程,2014,36(9):1 127-1 131. XIE Hui-chao,JIANG Chao,ZHANG Zhi-gang,et al.Vehicle ride comfort optimization based on interval analysis[J].Automotive Engineering,2014,36(9):1 127-1 131.(in Chinese)

[8] 徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70. XU Ze-shui,DA Qing-li.Possibility degree method for ranking interval numbers and its application[J].Journal of Systems Engineering,2003,18(1):67-70.(in Chinese)

[9] 王群.基于对称拉丁超立方设计的多目标进化算法[D].西安:西安电子科技大学,2011:29-43. WANG Qun.Multiobjective evolutionary algorithm based on symmetric Latin hypercube designs[D].Xi’an:Xidian University,2011:29-43.(in Chinese)

Optimization on Interval Uncertainty of Artillery Recoil Resistance

LI Rong,YANG Guo-lai,SUN Quan-zhao,XIAO Hui

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to reduce the force of artillery carriage and obtain the better recoil resistance,the optimization on interval uncertainty of recoil fluid-hole were conducted.The three-parameter interval was defined combining with tolerance,and then the uncertainty optimization model and algorithm based on three-parameter interval were established.Taking the dimension of fluid hole as the uncertainty variable,the interval optimization design of the shape size of control rod was carried out by using the method mentioned above.The outer diameter of the control rod with different tolerance-grades was optimized.Research results show that the peak interval of recoil resistance is reduced after the optimization,and the recoil resistance curve is more gentler with a better fullness.The synchronous optimization of the tolerance design and the design of the outer diameter of control rod was realized.The optimum design-scheme of the outer diameter of the control rod considering the workmanship and the recoil resistance was obtained.

artillery;recoil resistance;structure design;interval optimization;uncertainty dimension

2016-12-16

国防973计划项目(1503613249);国家自然科学基金项目(11572158)

李荣(1991- ),男,硕士研究生,研究方向为火炮结构优化与优选。E-mail:lirongwork@qq.com。

杨国来(1968- ),男,教授,博士生导师,研究方向为火炮现代设计理论与方法。E-mail:yyanggl@mail.njust.edu.cn。

TJ303

A

1004-499X(2017)02-0078-07