线性回归模型在电力系统中的应用设想

伊国鑫+马国福

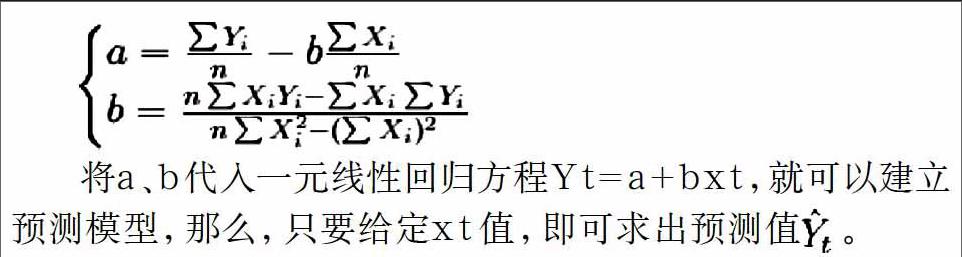
摘 要：回归分析是一种统计工具，它利用两个或两个以上变量之间的关系，由一个或几个变量来预测另一个变量，它是处理变量之间相关关系的一种数理统计方法。将该统计方法应用于预测电力系统运行中各种因素对设备状态量的影响，从而对设备的运维提供指导，具有可行性。

关键词：线性回归分析；预测；电力系统；设备状态量

中图分类号：TM715 文献标识码：A 文章编号：1671-2064（2017）11-0162-01

1 线性回归分析的意义

在客观世界中，我们经常会遇到一些相互依赖、相互制约的变量。它们之间有着一定的关系，这种关系在量上主要有两种类型.一类是确定性关系，也就是我们所熟悉的函数关系，其特点就是给定自变量的值，能确定因变量的对应值。另一类是非确定性关系，其特点是给定自变量的值，不能确定因变量的值。

回归分析是研究自变量的变化对因变量变化的影响程度，其目的在于根据已知自变量的变化来估计或预测因变量的变化情况。利用回归分析，确定因变量与自变量之间的回归模型；根据样本观测数据，估计并检验回归模型及未知参数；在众多的自变量中，判断哪些变量对因变量的影响是显著的，哪些变量的影响是不显著的；根据自变量的已知值或给定值来估计和预测因变量的值。

2 在电力系统中的应用

在电力系统运行过程中，一个设备运行参数的变化，往往会引起设备其他运行参数的变化，他们之间存在类似于线性的关系，例如：设备负荷电流的不同变化，引起设备接触面上发热温度的不同；或者设备负荷的不同引起设备电磁场场量的变化，从而引起设备局部放电放电量的大小变化。由于在系统运行过程中，对设备运行状态或者设备运行参数的影响，通常都是由多个影响因素，温度、湿度、电流、压力等等都会对设备的参数构成影响，并且这些影响因素对设备所构成的影响都不是确定的函数关系，因此，通过线性回归分析，构建各种影响因素对设备参数影响的模型，从回归分析入手，判断哪些变量对因变量的影响是显著的，根据自变量的已知值或给定值来估计和预测因变量的值，这对指导设备的状态检修、判断设备异常的发展趋势具有现实意义。

一元线性回归分析法的预测模型为：

将a、b代入一元线性回归方程Yt=a+bxt，就可以建立预测模型，那么，只要给定xt值，即可求出预测值。

将以上模型应用于电力系统中，例如，设备负荷电流的变化对设备接触面上发热温度的影响进行一元线性回归分析，则在以上模型中式中，xt代表设备t次负荷电流的值、代表t次设备接触面上的温升值。通过实际测试的一组数据，求出回归方程参数a、b的值，得到设备接触面上发热温度与设备负荷电流之间关系的线性回归方程Yt=a+bxt

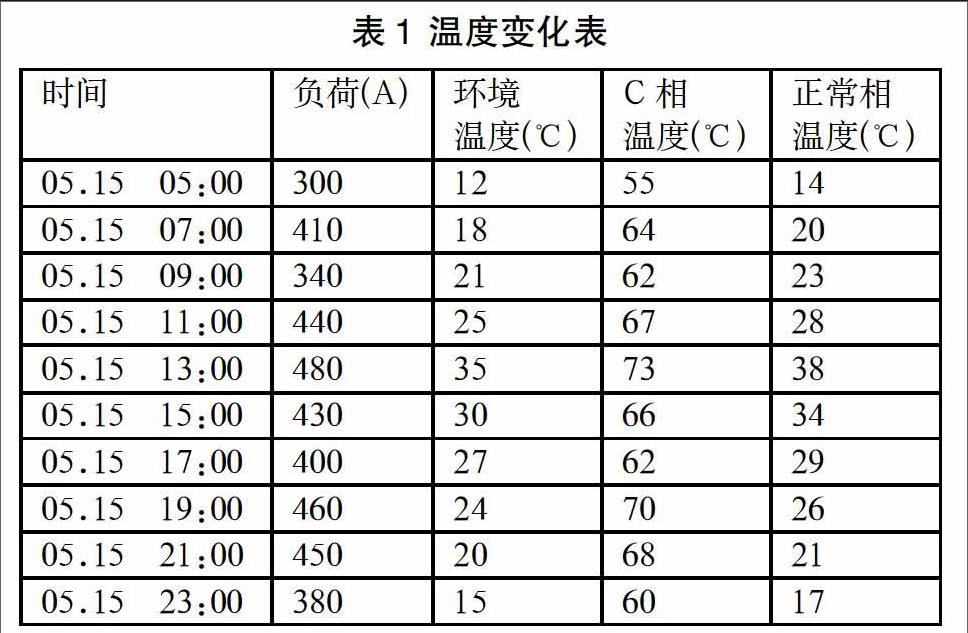
列如：某220kVxx变电站110kV隔离开关C相刀口发热，测得一天內的温度变化如下表1所示。只考虑负荷对测试温度的影响，忽略其他因素影响。

将19：00前的数据代入上述公式，计算求得：a=29.626b =0.087，即线性回归方程为Yt=29.626+0.087xt。通过该线性回归方程，我们验算21：00与23：00两个时间点的设备温度预测。将这两个时间点的参数带入以上方程，得到21：00的设备预测温度为：68.8℃，实际温度为：68℃，误差率为：-1.2%；23：00的设备预测温度为：62.7℃，实际温度为：60℃，误差率为-4.5%：这样，在设备运行过程中，我们可以通过该线性回归方程，可预测在不同的负荷电流下设备接触面上的温升值，从而制定相应的巡视、检修计划。

3 结语

类似于上述分析方法，线性回归分析可以运用于系统运行中所面临的各种不确定因素对设备影响的预测中，通过建立线性回归模型，预测设备状态量在相关因素影响下的发展趋势，从而指导设备的运维。

参考文献

[1]沈其君主编.SAS统计分析[M].东南大学出版社，2001.

[2]王学仁，王松桂，编译.实用多元统计分析[M].上海科学技术出版社，1990.

[3]上海师范大学数学系概率统计教研组 编.回归分析及其试验设计[M].上海教育出版社，1978.

[4]孙目珍.电介质物理基础[M].广州：华南理工大学出版社，2000.

[5]周泽存，沈其工，方瑜，等.高电压技术[M].北京：中国电力出版社，2007.

[6]严璋，朱德恒.高电压绝缘技术[M].北京：中国电力出版社，2007.