IGBT模块结壳热阻快速计算法研究

姚芳，胡洋，吴伟涛

（河北工业大学电气工程学院，天津 300130）

IGBT模块结壳热阻快速计算法研究

姚芳，胡洋，吴伟涛

（河北工业大学电气工程学院，天津 300130）

热阻是评价IGBT可靠性的重要指标。寻找简便高精度的测量方法对IGBT热阻进行测试具有十分重要的意义。根据JESD51—14中的瞬态热阻抗定义式，提出了一种可以快速、准确计算IGBT模块结壳热阻的方法。建立了根据不同散热系数下模块结温变化曲线的分离点求解模块结壳热阻的计算模型，制定了试验求解具体步骤。对所提出的方法和所设计的计算模型进行仿真研究和试验研究，并在实验室条件下验证了其可行性。

IGBT模块；结壳热阻；快速计算；瞬态热阻抗；模型

随着半导体技术的迅速发展以及绝缘栅双极型晶体管（insulated gate bipolar translator，IGBT）模块的普遍应用，对电力电子可靠性的要求越来越高，过热失效作为主要失效原因也成为阻碍IGBT器件发展的一大因素［1］。为了突破这一瓶颈，近年来国内外专家学者也把目光投入到IGBT模块热失效分析上［2-3］。热阻作为表征半导体器件热传导能力的参数，也成为热失效问题的研究重点［4］。

IGBT热阻的测试及计算方法常见的有以下几种，包括热传导法、热敏参数法［5-6］、物理接触法［7］、红外热成像法［8-9］、等效热网络模型法［10-11］等。

热传导法根据IGBT的定义式计算热阻。该方法的优点是以直接根据尺寸参数及材料热特性求解模块的结壳热阻，并可以清晰反映模块内部各层结构的热阻值，缺点是模块内部各层导热材料的厚度和有效导热面积均为近似值，并且忽略了各层材料热导率随温度及退化程度发生变化的情况。

热敏参数法首先得到温敏参数，由温敏参数求得IGBT的结温，再根据IGBT热阻的计算式求得其热阻。该方法优点是不易对器件造成破坏；缺点是引入了较多的测量误差，壳温最大值点难以确定，并且该方法需要在IGBT模块达到热稳态时才能进行求解。对此也有很多文献对该方法进行改进。

物理接触法包括使用热电偶、光纤探头等直接对结温或壳温进行测量。该方法的优点是直接可以得到测量点任意时刻的温度；缺点是一方面会对器件造成破坏，并且造成的破坏也会影响温度的分布情况，另一方面测量点可能并非温度最大值点，这都将带来误差。

红外热成像法是使用红外热成像系统进行测温。其优点是测量精度高，探测速度快；缺点是成本高。

等效热网络模型法通过利用计算机软件编程，对IGBT模块的瞬态热阻抗曲线进行拟合，得到其RC热网络模型，进而求得热阻。该方法优点是计算速度快；缺点是随着IGBT模块的不断退化，需要对热网络模型的阻容参数不断进行修正，工作繁琐。

根据以上分析可知，传统的热阻计算方法在准确性、测量周期或是成本上都有着些许缺陷，因此，本文根据瞬态热阻抗计算式提出了一种可以在工况条件下快速、准确计算IGBT模块结壳热阻的方法。

1 IGBT模块快速计算法原理

JESD51—14中定义，在t=0时刻给半导体器件施加1个恒定的热功率，那么t时刻的瞬态热阻抗可通过下式计算：

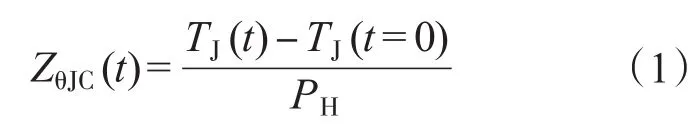
式中：TJ(t)为t时刻的芯片结温；TJ(t=0)为t=0时刻的芯片结温；PH为施加的热功率。

根据电热比拟理论，热阻作为材料自身属性，是固定不变的。但是热与电还有着根本的不同，电的传递速度即电场的传播速度非常快，而热的传播则相对比较缓慢，具有迟滞性。因此，以IGBT模块为例，在热量由芯片产生，向下传递的过程中，当t1时刻热量前端刚传递到衬底层（DBC）底面时，那么热量所流经材料的热阻为结到DBC底面的热阻，根据式（1）求得的ZθJC（t1）即结到DBC底面的热阻；当t2时刻热量前端传递到铜基板底面时，那么热量所流经的热阻则为模块结壳热阻，根据式（1）求得的ZθJC（t2）即结壳热阻。所以通过研究热量前端传递到铜基板底面的时间节点及该时刻的模块结温大小，根据热量的流经热阻，由式（1）就可求得模块的结壳热阻。

为了研究热量传递到铜基板底面的时间点，通过仿真研究某恒功率载荷下IGBT模块的结壳温度在0.02 s前的变化曲线，如图1所示。

图1 IGBT模块0.02 s前结壳温度变化曲线Fig.1 Junction-case temperature change curves before 0.02 s of IGBT

由图1可知，在t0时刻施加恒功率载荷后，芯片温度迅速上升，在0.02 s时刻升高了0.85℃，而壳的温度升高出现迟滞性，在0.014 s才有较为明显的升高，且温度变化速率要小于结温变化速率，在0.02 s时壳温升高了0.003℃左右。为了准确研究模块热能传递过程，对图1中的壳温变化曲线进行局部放大，如图2所示。

图2 IGBT模块0.01 s前壳温变化曲线Fig.2 Case temperature change curve before 0.01 s of IGBT

由图2可知，壳温在0.003 s前不发生变化，也就是说当t=0.003 s时，由芯片吸收的热量刚好传递到IGBT模块基板底面。

为了便于观察，只对模块中1组IGBT芯片的剖切面进行仿真，得出IGBT在0.003 s时的瞬态纵向分布，如图3所示。

图3 IGBT模块0.003 s温度瞬态纵向分布Fig.3 Temperature transient vertical distribution at 0.003 s of IGBT

图3中，热流的流动沿箭头方向由IGBT芯片流向铜基板底面。根据该仿真可知，在0.003 s时，热流刚好传到铜基板底侧，也证明了我们所提出的迟滞性理论。

通过图1～图3可知，热量从芯片传递到铜基板底面的时间为0.003 s，由于IGBT模块芯片到铜基板底面的垂直距离为4.75 mm，所以可以求得热量在IGBT模块中的平均传播速度为1.58 m/s，远低于电子在金属导体中的传播速度，因此热量的传递与电能传递相比具有迟滞性。

2 IGBT快速计算模型建立

根据对式（1）的分析可知，当tp时刻热量恰好传递至模块铜基板底面时，由式（1）所计算的瞬态热阻ZθJC（tp）是模块热量所流经的热阻和，即为模块的结壳热阻。

由图1可知，热量从模块芯片传递到铜基板底面的时间在10-3s数量级，非常短暂，因此使用该方法可快速计算模块结壳热阻，不用等到IGBT模块进入稳态传热模式时才能进行测量。因此，工况条件下使用该方法，可以在IGBT模块启动的瞬间获取模块的结壳热阻。

因为模块在工作前各点温度与环境温度相同，所以模块结壳热阻的计算方法如下式所示：

其中，tp满足：

式中：Ta为环境温度；Tc(t)为t时刻模块的壳温；tp为模块壳温刚开始升高的时间点。

根据以上研究表明，通过仿真能简单捕捉到壳温刚开始升高的时间点及对应时刻的结温。而在实际工况测量时，为了获取该时间节点，需要同时监测模块的结壳温度，根据模块的变化曲线拟合曲线方程，寻找ΔTc正好不为零时的tp值。但建立数学模型，并求导分析的过程繁琐，且在选取底壳温度测量点时具有随机性，因而导致结壳热阻计算结果产生误差。

为了可以准确获取tp时刻的结温TJ(tp),需要对IGBT模块的传热过程进一步分析。当给IGBT模块施加一恒定功率时，热量由芯片的PN结产生并垂直向下传递，当器件的壳温没有发生变化之前，通过式（1）求得的瞬态热阻大小不受模块外部散热条件的影响，只与模块内部散热性能有关。因此，对于散热条件不同的IGBT模块，由于在此时间段，热量的传递路径完全一致，所以模块的结温变化曲线也完全一致。随着时间的推移，由于IGBT模块铜基板底面温度升高而通过热对流的方式向环境中散失热量，此时通过式（1）求得的瞬态热阻大小将受模块外部散热的影响。对于不同的散热条件，IGBT模块的热量传递路径在此时刻后发生变化，结温曲线也出现分离。2个不同散热系数的IGBT模块，在施加相同热载荷时结温变化曲线如图4所示。

图4 不同散热系数下IGBT模块结温变化曲线示意图Fig.4 The temperature change curves under differentheat dissipation coeffcient of IGBT

由图4分析知，在tp时刻，热量刚好由芯片传递至模块铜基板底面；在tp时刻之前两模块热量传递路径及条件完全一致，所以对于不同散热系数的IGBT模块结温在此时间段变化曲线一致；在tp时刻后，热量开始由铜基板底面向环境中散失，由于采用不同的对流系数，两种模块的热量传递条件发生变化，结温升高速率也发生变化：对流系数较大的模块，结温变化率小，对流系数小的模块，结温变化率大。

3 IGBT模块快速计算仿真研究

为了验证所提出方法的正确性，通过有限元仿真对一案例进行求解计算。为了可以同时快速计算模块热阻，仿真中在同一工作平台建立2个完全一致的IGBT模块三维模型，并为它们设置不同的对流系数，以代替实际测量时的先后2次测量。具体求解过程如下。

1）在同一工作平台建立2个完全一致的IGBT模块3维模型，并进行完全相同的网络划分，如图5所示。

图5 同一工作平台2模块网络划分示意图Fig.5 Network partition sketch map of two IGBT in the same working platform

2）铜基板底面的对流系数分别设为50和100，仿真不同散热条件的模块传热特性。

3）给2个模块的IGBT芯片均施加功率为50 W的热载荷。

4）通过仿真获得IGBT模块的结温变化曲线如图6所示。

图6 不同散热系数下结温仿真曲线Fig.6 Junction temperature simulation curves under different heat dissipation coeffcient

由图6可知，在t=0.001 4 s时，2条结温曲线发生分离，分离时的结温大小为TJ（0.001 4）=33.3℃。

5）经过仿真可知，TJ（0.001 4）=33.3℃，Ta=25℃，P=50 W，根据式（2），求得IGBT模块的结壳热阻RJC=0.166℃/W。

通过热传导法求得的IGBT模块结壳热阻为0.168℃/W，通过等效热网络模型法求得的结壳热阻值为0.1672℃/W，IGBT使用手册中给出该试品未退化时的结壳热阻为0.167℃/W。这里，通过获取不同散热条件下结温变化曲线分离点求解的结壳热阻为0.166℃/W。对以上结果进行比较，验证了IGBT模块快速计算法的可行性与正确性。

4 IGBT模块快速计算试验研究

4.1 快速计算工况条件实现方法

根据以上分析，在实际工况条件下使用该模型计算IGBT模块结壳热阻的实现方法为：在同一坐标系下绘制不同散热条件下IGBT模块的结温变化曲线，2条曲线的分离点对应的时刻即为壳温刚开始升高的时间点tp,此时对应的结温大小即为TJ(tp)。这样就可以根据式（2）直接计算模块的结壳热阻。

在工况条件下通过该方法计算模块结壳热阻的具体步骤如下：

1）使IGBT模块在环境温度Ta下达到热稳态，即模块各节点温度均为Ta,没有热传递发生；

2）给IGBT模块施加一恒定功率P，采集其结温变化曲线；

3）改变IGBT模块的散热条件，如：装配散热器时，改变铜基板与散热器之间的导热硅脂厚度，不装配散热器时，施加或改变风冷的空气流速。再次施加恒定功率P，采集其结温变化曲线；

4）寻找2次采集的结温变化曲线分离点对应的结温大小TJ(tp)；

5）根据式（2）计算模块的结壳热阻。

为了使得测试过程更加快捷方便，可以提前测量不同条件下结温的变化曲线，形成数据库。这样，实际操作时只需测量1次结温变化曲线，再与数据库中同条件结温曲线进行比对即可。

4.2 快速计算实验条件实现方法

通过埋入光纤传感器可以实现在不改变模块自身传热特性的基础上准确测量芯片结温，本节将根据分离点求结壳热阻的方法，在实验室条件下测量模块结壳热阻。

根据制定的在工况条件下实验该方法的具体步骤，设计实验条件下结壳热阻测试的实现方法。

1）环境温度设置。为了更好地模拟工况条件，实验过程直接在实验室环境中进行，同时记录测试时刻环境温度的大小。

2）施加恒定功率。给IGBT模块施加30 A的恒定电流，由于出现结温分离点的时刻在几ms左右，所以给模块栅极施加+15 V，持续时间为1 s的脉冲信号。经测量计算，此时的产热功率为52.6 W。

3）设置不同散热系数。由于2次测量需要给模块设置不同的散热系数，所以实验过程中，第1次测量时，不做任何散热处理，第2次测量时给模块进行风冷。

4）结温采样。通过温度信号解调器可以将光纤探头采集的光信号处理后发送给PC机，通过PC机可进行曲线拟合等处理。试验时，通过计算机设置结温的采样频率为9 600 Hz，即每s可以采集9 600个温度值，每隔0.1 ms采样1次。经测量IGBT模块施加载荷时，环境温度为Ta=19.8℃。

4.3 快速计算实验条件结果及分析

严格按照以上实验室条件进行测试，2次实验采集的结温点如图7所示。

图7 试验结温采集点Fig.7 Experimental junction temperature acquisition point

由图7及采集点数据分析可知，2次测量结温分离点时刻结温为TJ(tp)=28.6℃。根据实验条件可知，Ta=19.8℃，P=52.6 W，根据式（2）求得模块的结壳热阻为RJC=0.167 3℃/W。

经过比对实验计算结果发现，使用结温分离点法计算模块结壳热阻准确度较高。同时，实验过程耗时短，无需等待模块进入热稳态，可实现快速测量。

通过分析试验过程，总结发现在工况条件下使用该方法也存在一些不足：1）工况条件下的IGBT模块都有封装结构，无法直接测量芯片结温；2）该测试方法需要在不同对流系数下进行2次测量，第1次结束后需等待IGBT模块冷却到环境温度才可进行下一次测量；3）在工况条件下IGBT模块都是装配散热器使用的，拆卸散热器或改变散热器与铜底板导热硅脂的厚度，工作会比较繁琐，并且影响IGBT模块的正常使用。

通过本文的分析可知，该IGBT模块结壳温度快速计算法具有以下优点：1）无需测量模块的壳温，消除了测量IGBT壳温时因选取节点的随机性而引入的计算误差；2）测量误差小，IGBT模块芯片各处温度分布差异很小，所以测量点选取的随机性对热阻计算的影响非常小，同时，环境温度和施加的恒定功率都可以在工况条件下准确测量；3）测量周期短，因为热量从模块芯片传递到铜基板底面的时间在10-3s数量级，因此给IGBT模块施加恒功率P的时间要求非常短，采集1个结温变化的曲线在几s内就可完成。

5 结论

本文为了探寻热阻的快速计算方法，提出了通过获取不同散热条件下结温变化曲线分离点来求解IGBT模块结壳热阻的方法。设计出了工况条件下通过该方法求解IGBT模块结壳热阻的实现方法和具体实验步骤，并对该方法进行了仿真分析以及试验分析，利用该方法均快速准确获得了IGBT模块的结壳热阻。总结知该方法具有计算误差小、测量周期短的优点，可以实现准确、快速测量模块结壳热阻的要求。

［1］Yang Yi-Che，Hsu Feng-Mao，Su Yen-Fu，et al.Thermal Anal⁃ysis and Reliability Assessment of Power Module Under Power Cycling Test Global-local Finite Element Method［C］//Micro⁃systems，Pachaging，Assmbly and Circuits Technology Confer⁃ence（IMPACT），2014：335-338.

［2］El Boubkari K，Azzopardi S，Theolier L，et al.Failure Initia⁃tion of IGBT Due to Emitter Contact Degradation：A 2D Fi⁃nite Elements Electro-thermal Multi-cell Simulation Ap⁃proach Under Hard Switching，Short-circuit and Avalanche Operations［C］//Applied Power Electronics Conference and Exposition（APEC），2013 Twenty-eighth Annual IEEE，2013：2048-2415.

［3］赖伟，陈民铀，冉立，等.老化试验条件下的IGBT失效机理分析［J］.中国电机工程学报，2015，35（20）：5293-5300.

［4］Low Khai Yen C.The Theory，Practice and Application of Thermal Resistance Measurements of IGBT Devices［C］//Electronic Manufacturing Technology Symposium（IEMT），2010 34th IEEE/CMPT Intermational，2010：1-10.

［5］Avenas Y，Dupont L.Evaluation of IGBT Thermo-sensitive Electrical Parameters Under Different Dissipation Condi⁃tion-comparison with Infrared Measurement［J］.Microelec⁃tronics Reliability，2012，52（11）：2617-2626.

［6］Butron Ccoa J A，Strauss B，Mitic G，et al.Investigation of Temperature Sensitive Electrical Parameters for Power Semi⁃conductors（IGBT）in Real-time Applications［C］//PCIM Eu⁃rope 2014，2014：1-9.

［7］杨旭，周雒维，杜雄，等.绝缘栅双极型晶体管结温测量方法及其发展［J］.电测与仪表，2012，49（2）：7-12.

［8］禹鑫，杜明星，窦汝振，等.IGBT功率模块键合线故障下的温度特性研究［J］.电力电子技术，2015，49（2）：55-57.

［9］Dupont L，Avenas Y，Jeannin P O.Comparision of Junction Temperature Evaluations in a Power IGBT Module Using an IR Camera and Three Thermosensitive Electrical Parameters［J］.IEEE Transactions on Industry Applications，2013，49（4）：1599-1608.

［10］Gradinger T，Riedel C.Thermal Networks for Time-variant Cooling Systems：Modeling Approach and Accuracy Require⁃ments for Lifetime Prediction［C］//Integrated Power Electron⁃ic Systems，International Conference on 2012 7th，2012：1-6.

［11］陈明，胡安，唐勇，等.绝缘栅双极型晶体管传热模型建模分析［J］.高电压技术，2011，37（2）：453-459.

Study on a Fast Calculation Method of Junction-to-case Thermal Resistance of IGBT Modules

YAO Fang，HU Yang，WU Weitao
（School of Electrical Engineering，Hebei University of Technology，Tianjin 300130，China）

Thermal resistance is an important index to evaluate the reliability of insulated gate bipolar translator（IGBT）.It′s very significant to find a simple and accurate method to measure the thermal resistance of IGBT.According to the analysis of the transient thermal impedance formula defined in JESD51—14，a fast，accurate calculation method of the junction-to-case thermal resistance of IGBT module was proposed.A calculation model was designed according to the separation point of the temperature changed curve of the module under different heat dissipation coefficient to solve the catculation merhod of the juntion-to-case resistance module，specific steps of test solution were also made.The simulation and experimental study of the proposed method and the computational model were carried out and its feasibilitied is verified under the laboratory conditions.

IGBT module；junction-to-case thermal resistance；fast calculation；transient thermal impedance；moduler

TM56

A

10.19457/j.1001-2095.20170614

2016-05-19

修改稿日期：2016-08-06

国家自然科学基金（51377044）；河北省科技支撑计划（13214303D，14214503D）

姚芳（1973-），女，硕士生导师，教授，Email：yaofang@hebut.edu.cn