基于可变形卷积神经网络的图像分类研究
2017-07-12欧阳针陈玮
欧阳针+陈玮

摘要:卷积神经网络(Convolutional Neural Networks,CNNs)具有强大的特征自学习与抽象表达能力,在图像分类领域有着广泛应用。但是,各模块较为固定的几何结构完全限制了卷积神经网络对空间变换的建模,难以避免地受到数据空间多样性的影响。在卷积网络中引入自学习的空间变换结构,或是引入可变形的卷积,使卷积核形状可以发生变化,以适应不同的输入特征图,丰富了卷积网络的空间表达能力。对现有卷积神经网络进行了改进,结果表明其在公共图像库和自建图像库上都表现出了更好的分类效果。
关键词:卷积神经网络;图像分类;空间变换;可变形卷积
DOIDOI:10.11907/rjdk.171863
中图分类号:TP317.4
文献标识码:A 文章编号:1672-7800(2017)006-0198-04
0 引言
图像分类一直是计算机视觉领域的一个基础而重要的核心问题,具有大量的实际应用场景和案例。很多典型的计算机视觉问题(如物体检测、图像分割)都可以演化为图像分类问题。图像分类问题有很多难点需要解决,观测角度、光照条件的变化、物体自身形变、部分遮挡、背景杂波影响、类内差异等问题都会导致被观测物体的计算机表示(二维或三维数值数组)发生剧烈变化。一个良好的图像分类模型应当对上述情况(以及不同情况的组合)不敏感。使用深度学习尤其是深度卷积神经网络,用大量图像数据进行训练后可以处理十分复杂的分类问题。
卷积神经网络是为识别二维形状而专门设计的一个多层感知器,这种网络结构对平移、缩放、倾斜等扰动具有高度不变性,并且具有强大的特征学习与抽象表达能力,可以通过网络训练获得图像特征,避免了复杂的特征提取与数据重建过程。通过网络层的堆叠,集成了低、中、高层特征表示。AlexNet等网络模型的出現,也推动了卷积网络在海量图像分类领域的蓬勃发展。
1 卷积神经网络
卷积神经网络是人工神经网络的一种,其“局部感知”“权值共享”[1]等特性使之更类似于生物神经网络,网络模型复杂度大大降低,网络训练更容易,多层的网络结构有更好的抽象表达能力,可以直接将图像作为网络输入,通过网络训练自动学习图像特征,从而避免了复杂的特征提取过程。
Yann LeCun等[2]设计的LeNet-5是当前广泛使用的卷积网络结构原型,它包含了卷积层、下采样层(池化层)、全连接层以及输出层,构成了现代卷积神经网络的基本组件,后续复杂的模型都离不开这些基本组件。LeNet-5对手写数字识别率较高,但在大数据量、复杂的物体图片分类方面不足,过拟合也导致其泛化能力较弱。网络训练开销大且受制于计算机性能。
2012年,在ILSVRC竞赛中AlexNet模型[3]赢得冠军,将错误率降低了10个百分点。拥有5层卷积结构的AlexNet模型证明了卷积神经网络在复杂模型下的有效性,并将GPU训练引入研究领域,使得大数据训练时间缩短,具有里程碑意义。AlexNet还有如下创新点:①采用局部响应归一化算法(Local Response Normalization,LRN),增强了模型的泛化能力,有效降低了分类错误率;②使用Dropout技术,降低了神经元复杂的互适应关系,有效避免了过拟合;③为了获得更快的收敛速度,AlexNet使用非线性激活函数ReLU(Rectified Linear Units)来代替传统的Sigmoid激活函数。
Karen等[4]在AlexNet的基础上使用更小尺寸的卷积核级联替代大卷积核,提出了VGG网络。虽然VGG网络层数和参数都比AlexNet多,但得益于更深的网络和较小的卷积核尺寸,使之具有隐式规则作用,只需很少的迭代次数就能达到收敛目的。
复杂的网络结构能表达更高维的抽象特征。然而,随着网络层数增加,参数量也急剧增加,导致过拟合及计算量大增,解决这两个缺陷的根本办法是将全连接甚至一般的卷积转化为稀疏连接。为此,Google团队提出了Inception结构[5],以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能。以Inception结构构造的22层网络GoogLeNet,用均值池化代替后端的全连接层,使得参数量只有7M,极大增强了泛化能力,并增加了两个辅助的Softmax用于向前传导梯度,避免梯度消失。GoogLeNet在2014年的ILSVRC竞赛中以Top-5错误率仅6.66%的成绩摘得桂冠。
网络层数的增加并非永无止境。随着网络层数的增加,将导致训练误差增大等所谓退化问题。为此,微软提出了一种深度残差学习框架[6],利用多层网络拟合一个残差映射,成功构造出152层的ResNet-152,并在2015年的ILSVRC分类问题竞赛中取得Top-5错误率仅5.71%的成绩。随后,对现有的瓶颈式残差结构进行改进,提出了一种直通结构[7],并基于此搭建出惊人的1001层网络,在CIFAR-10分类错误率仅4.92%。至此,卷积神经网络在越来越“深”的道路上一往直前。
2 可变形的卷积神经网络
2.1 空间变换网络
空间变换网络(Spatial Transformer Network,STN)[8]主要由定位网络(Localisation net)、网格生成器(Grid generator)和可微图像采样(Differentiable Image Sampling)3部分构成,如图1所示。
定位网络将输入的特征图U放入一个子网络(由卷积、全连接等构成的若干层子网络),生成空间变换参数θ。θ的形式可以多样,如需要实现2D仿射变换,那么θ就是一个2×3的向量。
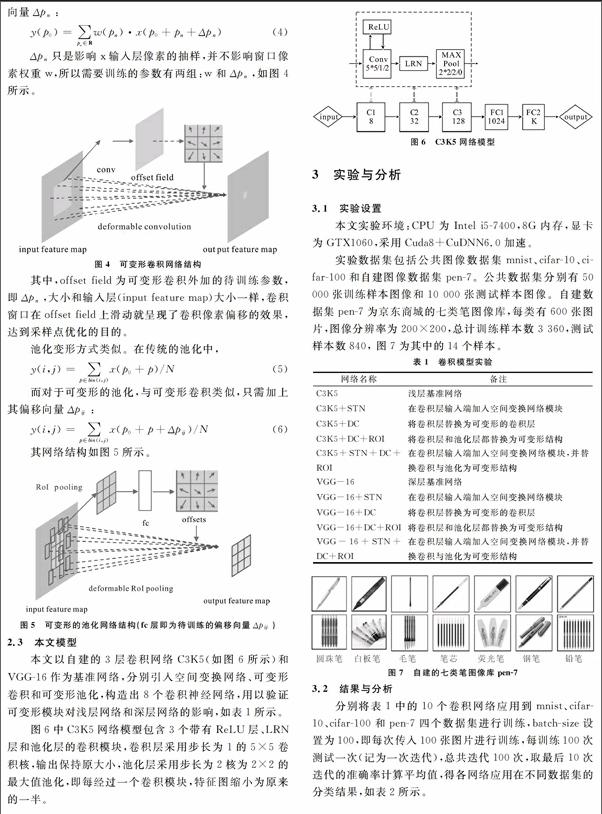
2.3 本文模型
本文以自建的3层卷积网络C3K5(如图6所示)和VGG-16作为基准网络,分别引入空间变换网络、可变形卷积和可变形池化,构造出8个卷积神经网络,用以验证可变形模块对浅层网络和深层网络的影响,如表1所示。
图6中C3K5网络模型包含3个带有ReLU层、LRN层和池化层的卷积模块,卷积层采用步长为1的5×5卷积核,输出保持原大小,池化层采用步长为2核为2×2的最大值池化,即每经过一个卷积模块,特征图缩小为原来的一半。
3 实验与分析
3.1 实验设置
本文实验环境:CPU为Intel i5-7400,8G内存,显卡为GTX1060,采用Cuda8+CuDNN6.0加速。
实验数据集包括公共图像数据集mnist、cifar-10、cifar-100和自建图像数据集pen-7。公共数据集分别有50 000张训练样本图像和10 000张测试样本图像。自建数据集pen-7为京东商城的七类笔图像库,每类有600张图片,图像分辨率为200×200,总计训练样本数3 360,测试样本数840, 图7为其中的14个样本。
3.2 结果与分析
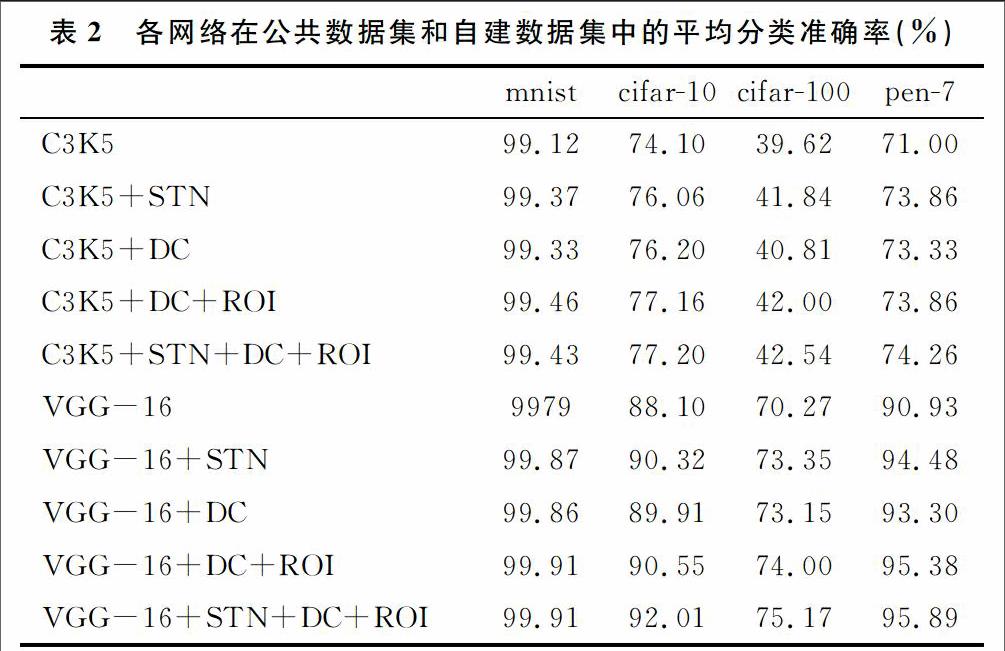
分别将表1中的10个卷积网络应用到mnist、cifar-10、cifar-100和pen-7四个数据集进行训练,batch-size设置為100,即每次传入100张图片进行训练,每训练100次测试一次(记为一次迭代),总共迭代100次,取最后10次迭代的准确率计算平均值,得各网络应用在不同数据集的分类结果,如表2所示。
实验结果表明,在卷积网络中引入空间变换网络、用可变形的卷积层和可变形的池化层替换传统的卷积层和池化层,不管是在浅层网络还是在深层网络,都能获得更高的分类准确率,这验证了空间变换网络和可变形卷积(池化)结构,丰富了卷积神经网络的空间特征表达能力,提升了卷积网络对样本的空间多样性变化的鲁棒性。包含3种模块的网络获得了最高的分类精度,使空间变换网络、可变形卷积层和可变形池化层在更多应用场景中并驾齐驱成为可能。
4 结语
通过在现有卷积神经网络中引入空间变换网络、可变形的卷积层和可变形的池化层,使得卷积网络在mnist、cifar-10、cifar-100及自建的pen-7数据集中获得了更高的分类精度,包含3种模块的网络获得了最高分类精度,证明了空间变换网络、可变形的卷积层和可变形池化层都能丰富网络的空间特征表达能力,协同应用于图像分类工作,这为后续研究打下了坚实的基础。
参考文献:
[1]BOUVRIE J. Notes on convolutional neural networks[J].Neural Nets,2006(1):159-164.
[2]Y LECUN,L BOTTOU,Y BENGIO,et al.Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[3]KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]. International Conference on Neural Information Processing Systems. Curran Associates Inc,2012:1097-1105.
[4]SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. Computer Science, 2014(6):1211-1220.
[5]SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[J]. CVPR, 2015(3):1-9.
[6]HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]. Computer Vision and Pattern Recognition. IEEE, 2015:770-778.
[7]HE K, ZHANG X, REN S, et al. Identity mappings in deep residual networks[J]. arXiv,2016(1603):5-27.
[8]JADERBERG M, SIMONYAN K, ZISSERMAN A, et al. Spatial transformer networks[J].Computer Science, 2015(5):1041-1050.
[9]DAI J, QI H, XIONG Y, et al. Deformable convolutional networks[J]. arXiv: 2017(1703):62-111.
(责任编辑:杜能钢)
英文摘要Abstract:Convolutional neural networks (CNNs) have powerful abilities of self-learning and abstract expression and they have gained extensive research and wide application in the field of image classification. However, since each module has a fixed geometric structure, it fundamentally limits the modeling of spatial transformation by convolutional neural networks, and is inevitably affected by the spatially diversity of data. The involve of a self-learning spatial transform structure and the deformable convolutional which can change its shape to adapt different input feature are both enrich the spatial expression ability of convolutional networks. In combination with the two characteristics, the existing convolutional neural networks are improved, and a better classification result is obtained in both the public image library and my own image library.
英文关键词Key Words: Convolutional Neural Network; Image Classification; Spatial Transform; Deformable Convolutional
