基于决策树的呼叫中心分时段话务量预测模型
2017-07-12王三军杨厚新王向英
王三军+杨厚新+王向英
摘要:为解决交通服务热线12328呼叫中心坐席安排难的问题,提高坐席人员工作效率,针对呼叫中心分时段话务量特性,提出了由预测分时段话务量占当日总话务量比例间接得出分时段话务量的思路,并以比例向量作为叶节点构建决策树模型。应用分类和回归树算法构建决策树时,考虑到分时段话务量样本间的相关性,引入马氏距离对算法中度量切分误差的方法进行改进。结合实际需求,对常用的误差衡量标准进行了修改,以更好地反映分时段话务量预测效果。实验证明,相比于直接预测分时段话务量,该方法预测误差降低了8%,提升了预测准确性。
关键词:呼叫中心;分时段话务量;分类和回归树算法;决策树;预测误差
DOIDOI:10.11907/rjdk.171968
中图分类号:TP319
文献标识码:A 文章编号:1672-7800(2017)006-0138-04
0 引言
为了畅通群众交通运输服务监督渠道,建立交通运输服务监督业务协同处理工作机制,提升交通运输行业科学决策水平,交通运输部自2013年开通全国服务监督电话,建设部、省、市三级联网运行的交通运输服务监督电话系统[1-2]。服务监督电话系统要达到提高服务监督质量、建立协同工作机制、提升科学决策水平的目的,必须实现呼叫中心坐席的科学安排。而话务量数据是坐席安排的关键依据,针对不同的话务量安排对应的坐席,使得在满足呼叫中心服务水平的前提下,实现人力资源最优配置。
话务量具有高度的非线性和时变特性[3],传统的经验排班模式难以准确预知话务量大小,无法满足实际生产需求。话务量分析旨在对未来话务量进行预测,以此来合理分配资源,从而进行科学的呼叫中心坐席安排。因此准确有效的话务量预测,对交通运输服务监督电话系统建设有重要意义。
现阶段,国内外很多研究机构都设计有话务量的预测模型,并且取得了丰富成果,主要有自回归移动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)[4-5]、神经网络[6-8]、灰色模型[9]、支持向量机[10]、k近邻算法[11-13]以及一些组合模型[14-15]。日话务量的预测准确度基本上可以满足实际需求,但每半小时的分时段话务量预测却缺乏相应研究,而后者在实际排班应用中具有非常重要的指導价值。针对分时段问题,本文提出一种先预测分时段话务量占当日话务量的比例,再得到分时段话务量值的间接预测思路,并以比例组成的向量作为决策树叶节点进行建模。在构建决策树过程中,考虑到话务量样本间的相关性,改进了分类和回归树(Classification and Regression Tree,CART)算法中度量划分数据集误差的方法。实验证明,应用这种思路和改进的方法进行预测相比于直接预测各时段话务量值,预测误差降低了8%。
1 决策树模型
1.1 决策树
决策树是机器学习中用于分类和回归的一种主要预测模型,代表对象属性与对象值之间的映射关系[16]。它从一组表面上看似无序的数据集中学习出决策规则,采用自顶而下的递归方式,构建出决策树模型。因此,决策树本身就是由IF-THEN组成的规则集合,从根节点到叶节点的路径对应着一条决策规则。在决策树算法中,分类和回归树是一种通用的算法,采用简洁的二叉树结构,既可用于分类,也可用于回归,目前已得到广泛研究和应用。本文将CART算法用于构建分时段话务量预测模型,并针对话务量数据的特性,对其中划分误差的度量标准进行讨论和改进。
1.2 改进的CART算法
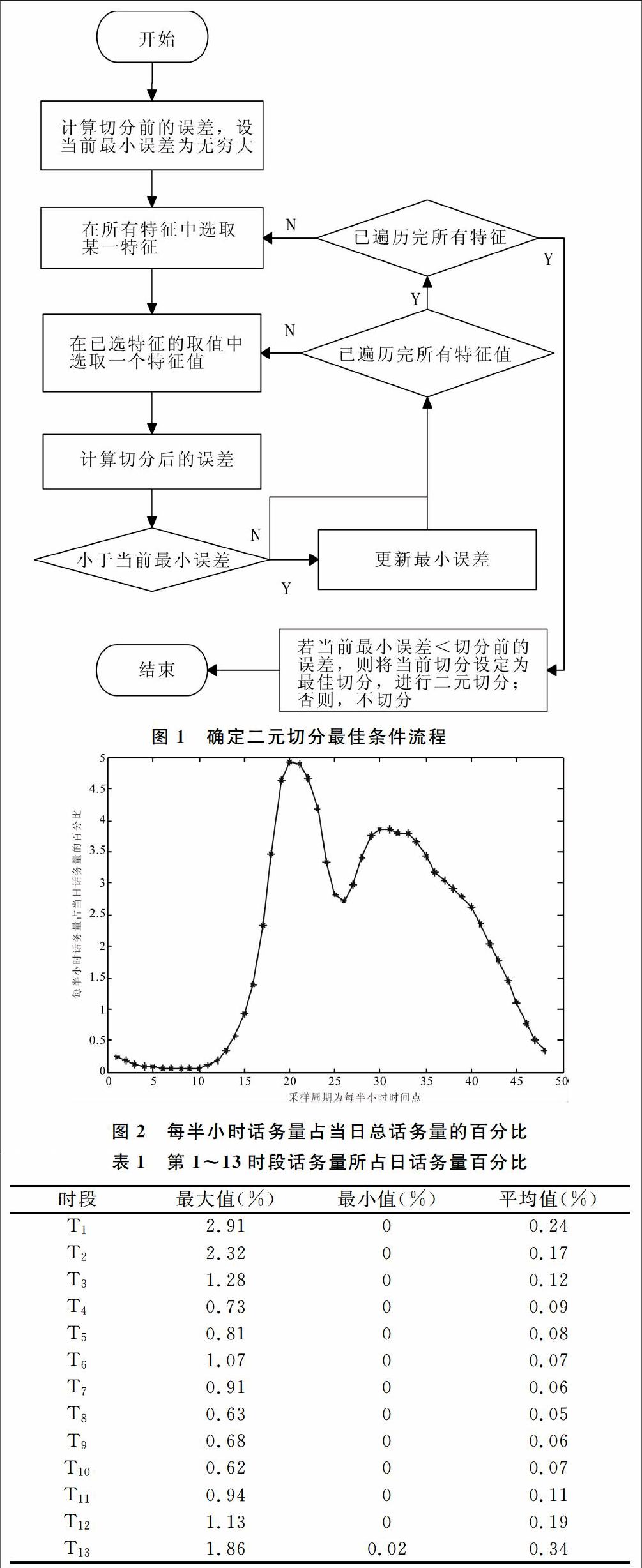
根据实际情况,选取季节、日期类型(1工作日、2周末、3节假日)、最高温、最低温、平均温、降雨、降雪、风力等因素作为影响话务量的特征,按图1所示的流程图判断是否进行二元切分以及如何确定最佳切分条件。
在构建决策树时,根据特征及特征值对数据集进行二元切分。通过遍历所有的特征及其可能的取值,找到使误差最小化的切分点,确定最佳的切分特征以及在该特征上切分的最佳位置。如果节点的特征值大于对应的切分特征值,那么该节点被划分为左子树节点,否则该节点被划分为右子树节点。然后再分别对左、右子树的数据集执行上述二元切分的操作。为了反映一次切分效果,采用式(4)的形式度量切分误差。
为了控制构建决策树过程中的切分终止条件,在决策树模型中引入两个参数,α和β。其中,参数α是容许的总方差减少量阈值,如果一次切分后,数据集的总方差减少量小于该阈值,则停止切分,否则继续切分。参数β是切分后节点中的最少样本数。如果一次切分之后,某一个节点中的样本数小于该参数,则说明该节点中的样本数量达到了设定的下限,为了防止叶子节点中的样本数量过少,停止切分。这两个参数的取值可以通过可视化视图,观察在不同取值组合下决策树模型对训练集数据的预测值与训练集中实际值的拟合情况确定。构建出决策树之后,对每个叶节点的话务量比例取均值得到该叶节点的值。因此,构建出的决策树叶节点都是1×48的向量。
1.4 决策树优化
如果决策树模型中节点过多,可能出现过拟合问题,可通过交叉验证[18]的方法来判断。在构建决策树时,已经通过参数α和β来为决策树的切分设定了终止条件,这实际上是对决策树进行了预剪枝操作。但是,在实验中发现构建出的决策树对这两个参数十分敏感。如果输入的参数过于严格,则构建出的决策树叶节点很少,甚至只有一个;反之,如果设定的参数不够严格,则构建出的决策树结构非常复杂。可见单一的预剪枝操作并不足以优化决策树,因此,进行后剪枝操作是必要的。
所谓后剪枝,就是用测试集数据验证已构建的决策树结构的合理性,如果有不合理的划分则采取相应的方法调整树结构。具体方法是从上至下遍历树中每个节点,计算将当前两个节点合并后的误差,并与合并前的误差相比较。若误差减小,则合并;否则保留原结构。将预剪枝与后剪枝操作结合使用能够有效地优化决策树的结构,解决过拟合问题。
2 分时话务量预测
2.1 历史话务量分析
呼叫中心主要承担了业务咨询、故障报修、投诉等职责[19],显然,这些业务受天气、季节、节假日以及资费政策等不确定性因素的影响,因此每天的话务量也随之变化,而各时段话务量的特性还需要进一步分析。以某省2014年12月24日至2016年11月30日的话务量为例进行分析,图2展示了这段时期内每半小时话务量占当日总话务量比例的平均值,在48个时段中出现了两个峰值,两个谷值,在某些时段内话务量占比非常小。一般在第19~22时段(上午9时~11时)达到一个峰值,通常称为早忙时,然后出现一个谷值,在第30~32时段(下午3时~4时)达到另一个峰值,通常称为晚忙时,而在第6~10时段(凌晨3时~5时)达到最低点。
以yij,j=1,2,...,48表示各个时段的话务量,yi表示日话务量,则满足yij<0.5%*yi的时段有13个,即第1~13时段。表1显示了这13个时段的话务量占当日话务量的百分比,可以看出各些时段占日话务量的百分比值最大不超过3%,最小为0,平均值在0.1%左右,分布稳定,波动范围较小。进一步分析原始数據得出,第1~13时段内的话务量之和占日话务量的平均百分比为1.6%,最大值不超过10%,且这些时段内的话务量均值都不超过50。
2.2 数据预处理
分析话务量数据时发现其中出现了一些离群点。形成离群点的原因是多种多样的,可能是在采样过程中发生的误差,如记录过程中出现笔误、计算错误等,也可能是偶然发生突发事件导致的。无论何种原因,这些离群点均会对研究整个数据集的规律产生一定影响。因此,在进行预测之前,对数据进行预处理是必要的,这个过程包括异常数据的识别和处理。
通过对日话务量的分析发现,每月的日话务量序列Z服从正态分布,记作Z~N(μ,δ2),其中,μ和δ分别为当月日话务量数据的平均值和标准差,故用[μ-2δ,μ+2δ]的区间作为判断日话务量数据是否正常的标准,落在这个区间内的数据看作是正常数据,超出这个区间的数据看作是异常数据。为了避免异常数据对构建预测模型的干扰,若识别出某天的日话务量数据为异常数据,则将当天的话务量数据剔除。
2.3 评价方法
通过2.1节对分时段话务量数据的分析,发现一天之中第1~13时段话务量相对较少,最高不到总话务量的10%,而且每天这些时段话务量分布规律非常稳定,仅在极小的误差范围内波动,所以这些时段的话务量预测绝对误差很小。而第14~48时段集中了一天中绝大部分的话务量,所以在对分时段话务量预测效果进行评价时,用这35个时段的话务量预测平均误差来反映该天分时段话务量预测的效果。误差采用常用的平均绝对相对误差(Mean Absolute Percentage Error, MAPE)[20]来衡量,则评价分时段话务量预测误差(Component Mean Absolute Percentage Error, CMAPE)的方法的形式如下:
3 实验结果及分析
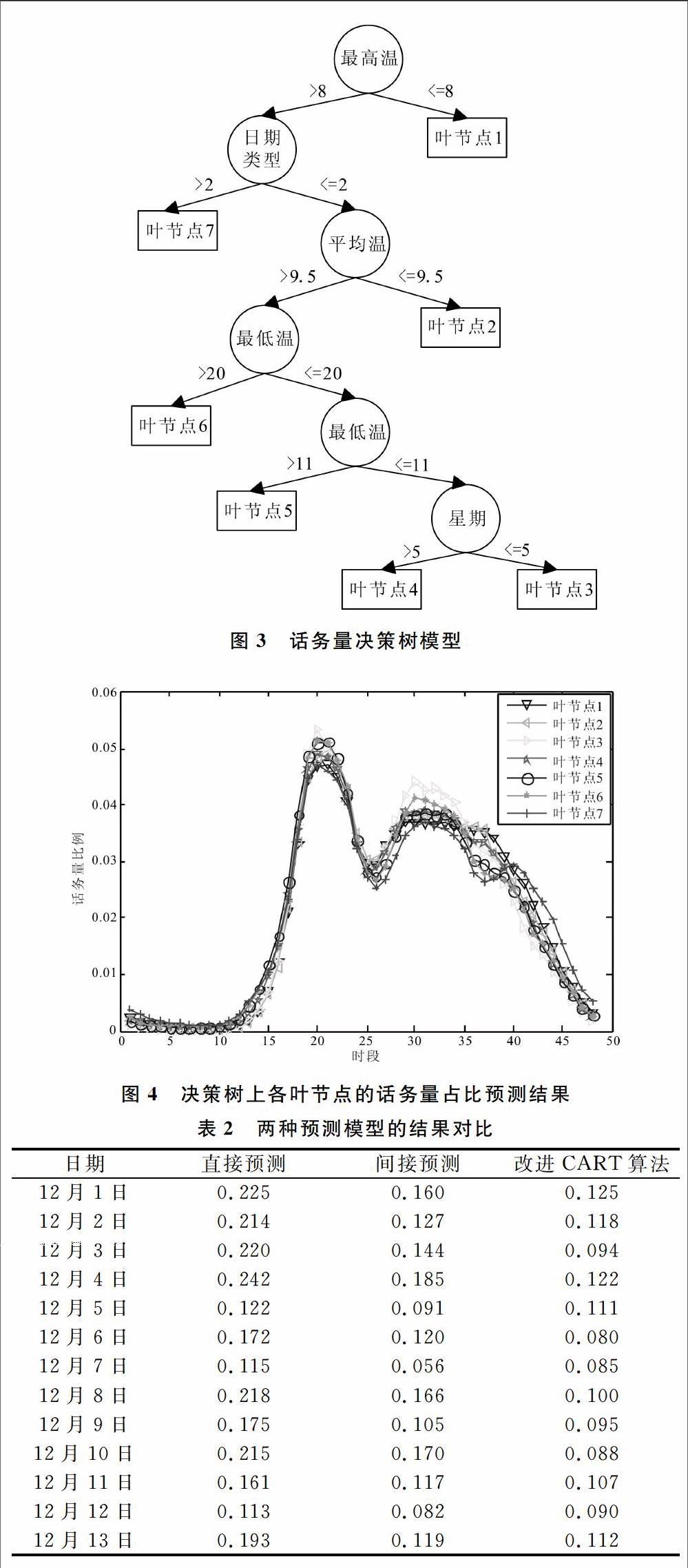
使用Python编写程序实现上文提出的分时段话务量预测思路和建模方法,以某省分时段话务量数据为例进行实验。实验中所采用的数据集包括了每天的总话务量、对应的48个时段的话务量以及话务量特征。以2014年12月24日至2016年11月10日的数据为训练集,以2016年11月11日至2016年11月30日的数据为测试集,预测2016年12月1日至2016年12月15日期间的分时段话务量,并用CMAPE的形式对预测效果进行评价。使用训练集数据学习决策树模型,再用测试集数据对模型进行剪枝,最终得到的决策树模型如图3所示。可以看出,构建的决策树模型为7层二叉树,结构简单,容易理解。温度、日期类型、星期(一周中的第几天)对话务量有很大影响。可以根据决策树模型对应的规则集推理出理论上的分时段话务量比例大小。
模型中共有7个叶节点,如图4所示,每个叶节点表示48时段占全天话务量比例的向量。从图中可以看出,在前18个时段,7个叶节点的值都很接近,接着在后面时段中出现第一个峰值时,各节点出现峰值的时段略有不同且峰值的高低也有较大的差别,接下来各节点值都有所降低,并出现一个短暂的谷值,26时段之后各节点表现出不一样的大小和变化趋势,尤其是第7个叶节点。
同时,采用直接预测分时段话务量的思路,同样使用决策树模型对相同时间段内的话务量进行预测,作为第一组对比实验。直接预测的方法是,首先将分时段话务量按照不同时段进行分类,这样就得到48个不同时段的数据集,然后再分别对每个时段的话务量进行预测。另外,采用间接预测分时段话务量的思路和改进CART算法构建决策树模型对相同时间段内的话务量进行预测,作为第二组对比实验。三种方法得到的预测误差情况如表2所示。
统计得出直接预测这15天话务量的平均误差是0.184,间接预测的平均误差是0.124,间接预测且采用改进CART算法的平均误差是0.100。间接预测的误差相比于直接预测有所降低,预测准确性提高了6%,改进CART算法后,预测准确性达到90%。
4 结语
根据分时段话务量特性,本文提出了由预测分时段话务量比例间接得到分时段话务量的思路,并用分时段话务量比例组成的向量作为叶节点构建决策树模型。在运用CART算法生成决策树时,解决了算法在度量划分误差时未考虑样本间相关性的问题。考虑到分时段话务量的分布特性以及呼叫中心的实际需求,修改了计算预测误差的方法,以更好地评价预测效果。最后通过实验验证了这种思路与改进建模方法的可行性和有效性。相比于直接预测,间接预测和改进CART算法预测分时段话务量准确性有所提高,但仍出现了个别预测准确性不理想的情况,这是下一步研究需要解决的问题。
参考文献:
[1]中华人民共和国交通运输部.交通运输部关于改进提升交通运输服务的若干指导意见[Z].中华人民共和国交通运输部,2013.
[2]李泓波,彭三城,劲波,等.一类决策树ID3改进算法探究[J].2016,15(2):30-32.
[3]邓波,李健,孙涛,等.基于神经网络的话务量预测[J].成都信息工程学院学报,2008,23(5):518-521
[4]SHULAN LI,HONGQIONG HUANG,DAQI ZHU,et al.The application of space-time ARIMA model on traffic flow forecasting[C].Proceedings of the 2009 International Conference on Machine Learning and Cybernetics.Piscataway,NJ:IEEE,2009:3408-3412.
[5]KAMARIANAKIS Y,SHEN W,WYNTER L,et al.Rejoinder:real-time road traffic forecasting using regime-switching space-time models and adaptive lasso[J].Applied Stochastic Models in Business and Industry,2012,28(4):297-315.
[6]SARDHAN,SSATSRI,VCHUTCHAVONG,et al.Improved model for traffic fluctuation prediction by neural network[C].Proceedings of the 2007 International Conference on Control,Automation and Systems.Piscataway,NJ :IEEE,2007:122-125.
[7]DANG X C,HAO Z J,LI Y,et al.Network traffic forecasting combination model based on wavelet transform and chaos algorithm[J].International Journal of Wavelets,Multiresolution and Information Processing,2014,12(03)..
[8]LONG H,YAN G.Forecasting import and export volume with a combined model based on wavelet filtering[J].International Journal of Wavelets,Multiresolution and Information Processing,2016,14(3):19-25.
[9]乐可争.基于灰色预测模型的移动话务量预测研究[D].上海:东华大学,2014.
[10]陈电波,徐福仓,吴敏.基于聚类和支持向量机的话务量预测模型[J].控制工程,2009,16(2):195-198.
[11]SHUANGSHUANG LI,ZHEN SHEN.A k_nearest neighbor locally weighted regression method for short-term traffic flow forecasting[C].//Proceedings of the 2012 IEEE International Conference on Intelligent Transportation Systems.Piscataway,NJ:IEEE,2012:1596-1601.
[12]BERNAS M,PLACZEK B,PORWIK P,et al.Segmentation of vehicle detector data for improved k-nearest neighbours-based traffic flow prediction[J].Iet Intelligent Transport Systems,2015,9(3):264-274.
[13]DELLACQUA P,BELLOTTI F,BERTA R,et al.Time-aware multivariate nearest neighbor regression methods for traffic flow prediction[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(6):3393-3402.
[14]SHEN DONG,LIGUANG SUN,TANGHSIEN CHANG,et al.Combined short-term traffic flow forecast model for beijing traffic forecast system[C].Proceedings of the 2011 International IEEE Conference on Intelligent Transportation Systems.Piscataway,NJ:IEEE,2011:638-643.
[15]何玮珊,覃锡忠,贾振红,等.基于小波变换和ARMA-LSSVM的忙时话务量预测[J].计算机工程与设计,2014,35(12):4105-4108.
[16]徐鹏,张岩江,苏森.PaaS云资源调度技术研究[J].华中科技大學学报:自然科学版,2013,41(S2):52-56.
[17]张翔,王士同.一种基于马氏距离的可能性聚类方法[J].数据采集与处理,2011,26(1):101-105.
[18]BAI JING,YANG LIHONG,ZHANG XUEYING.Parameter optimization and application of support vector machine based on parallel artificial fish swarm algorithm[J].Journal of Software,2013,8(3):673-679.
[19]夏正洪,潘卫军.呼叫中心智能排班系统关键技术[J].计算机工程与设计,2015,36(5):1332-1336.
[20]刘童,孙吉贵,张永刚.用周期模型和近邻算法预测话务量时间序列[J].吉林大学学报:信息科学版,2007,25(3):239-245.
(责任编辑:陈福时)
