涡轮增压柴油机叶轮疲劳仿真及试验
2017-07-12杨玲玲席德明
杨玲玲+席德明
【摘 要】本文以增压器叶轮为研究对象,以满足涡轮增压柴油机性能为研究目的,基于有限元法及局部应变疲劳理论,着重分析叶轮等效应力及应变的分布情况,预测叶轮的疲劳循环次数及仿真寿命计算,将增压器安装到柴油机上进行试验研究,结果表明对叶轮的仿真及疲劳分析具有可行性。
【关键词】柴油机 涡轮增压器 叶轮 疲劳 史密斯公式
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)05C-0190-03
现如今,涡轮增压器早已被大量使用在柴油机中,尤其是车用及船用发动机。增压器可以提高发动机热效率、改善发动机尾气净化排放等,在提高柴油机性能和降低空气污染方面发挥着巨大作用。在涡轮增压技术中,由于叶轮部件的高速旋转可以显著提高过滤后的空气动能,压缩更多的空气进入气缸,使燃油燃烧更充分,从而增加发动机的输出功率。叶轮作为增压器的关键部件起着举足轻重的作用。影响压气机性能的叶轮结构参数有很多,例如压气机的进口直径、叶形、叶片进出口角、叶高等。因此,在叶轮的设计中,既要满足空气动力学原理以确保良好的工作性能,同时又要保证叶轮叶片具有足够的强度及刚度以适应发动机在高原等极端环境条件下的正常工作。涡轮增壓器特别是车用增压器,由于其经常在交变载荷下工作,所以叶轮的疲劳破坏成为主要的破坏形式。本文以某型号增压器叶轮零件为研究对象,考虑其在高速运转下的载荷情况,以CAE软件为分析平台对叶轮进行仿真分析,运用疲劳理论可视程序化对疲劳寿命进行预测。最后以发动机考核试验的试验结果对理论分析进行了验证,发现此型号叶轮疲劳寿命满足发动机工作需求,为叶轮的设计工作提供理论依据。
一、叶轮工作时的低周疲劳
涡轮增压器是一种叶轮机械,涡轮和压气机叶轮是涡轮增压器的关键部件。增压器叶轮在工作时转速逐渐增大,车用涡轮增压器工作转速一般为100000r/min左右,最高转速已达300000r/min,所以无法避免会产生应力集中造成的局部应力增大。而在局部高应力处由于叶轮旋转次数不断叠加,塑性应变也在逐渐积累。这种逐渐积累的塑性应变能或塑性应变将导致低周疲劳破坏的产生。涡轮增压器在实际工况中处于高速旋转,叶轮不仅承载空气对叶片的反作用力,而且承载旋转产生的高速离心力。由高的交变应力引起的低周疲劳破坏是增压器失效的主要模式之一。因此,通过增压器低周疲劳试验考核低周疲劳寿命具有重要意义。
二、有限元模型仿真计算
(一)叶轮模型建立
本文所研究的叶轮材料为铝合金C355T61,弹性模量E=6.9x104Mpa,泊松比0.31。由于叶轮的外形结构较为复杂,本文中先在Pro/E中创建叶轮的三维模型,之后将建立好的模型导入ANSYS中。对模型进行网格划分。增压器叶轮有限元模型如图1所示。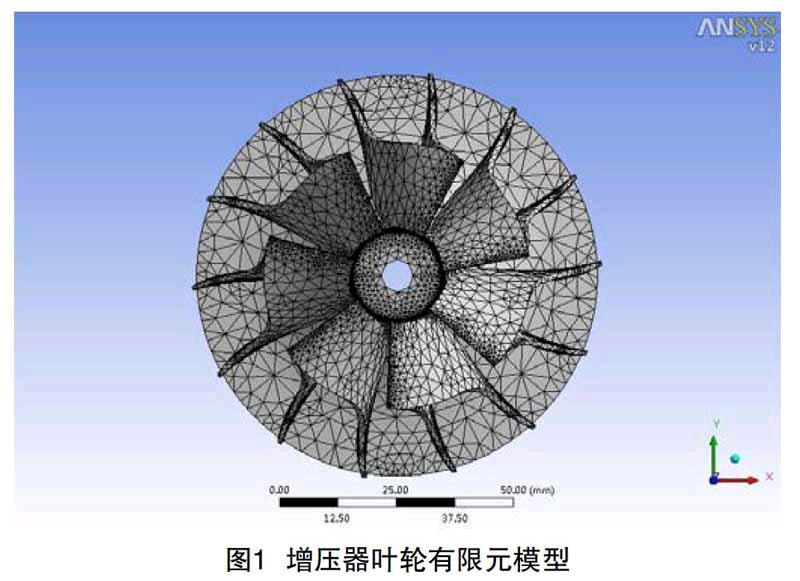
(二)叶轮强度计算及分析
在实际工作中,叶片牢固在底盘上,本次分析对叶片根部设置为全约束。叶轮前端轴向位移被约束,内径周向位移被约束。设置结束后进行强度仿真,其结果分别如图2—5所示。
从分析结果可以看出,当转速为72216r/min时,叶轮应力接近于屈服极限。在叶轮高速旋转中,导风轮最大应力位于内径底部,而叶轮根部有较为明显的应力集中点。说明离心力是使叶片在工作中遭受破坏的主要来源,且破坏点主要集中在叶片根部。最大等效应力为193.79Mpa,最大主应力为276Mpa。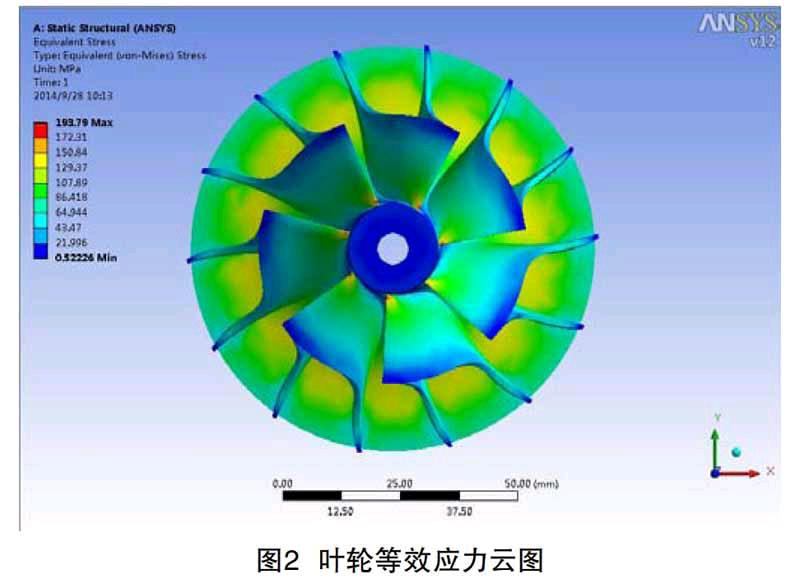
三、叶轮的疲劳仿真分析
(一)局部应变法
机械产品日常作业时,在产品的工作寿命和自身抗疲劳强度中起到决定性作用的是产品部件上所产生的局部应力及形变的最大值,零件往往是从最大局部应变处出现疲劳的。这种理论考虑的关键点是如果一个产品部件产生疲劳现象,其源头基本是位于应力变形集中处首先出现的裂纹,且在其发生之前,均伴随有一定程度上的塑性形变,这种形变行为正是导致零部件出现裂纹继而扩展的首要前提。对于车轮这种工作中承受多重复杂工况的产品而言,一些微小的应力也会触发部件出现较大的应变。零部件中应力较为集中位置的应变最大值是影响产品工作使用寿命的重要因素。此方法基于寿命与应变关系,考虑疲劳损伤的作用,被应用于机械零部件疲劳寿命计算。
其中,为局部应变幅值,为局部应力幅值,E为弹性模量,为循环强度系数,为循环应变硬化指数。
此理论在前人学者不断研究试验的基础上,有众多方法理论相应问世,其中莫罗修正理论指出在零件出现塑性形变处,应力松弛造成其效果很小。故弹性形变处是受到平均应力波及的多数位置。根据上述原因,把平均应力转化为与之等同的对称应力幅值并综合平均应力作用的寿命应变公式:
其中,为局部应变幅值;为疲劳强度系数;为疲劳延性系数;为平均应力;E为弹性模量;n为疲劳寿命;b为疲劳强度指数;c为疲劳延性指数。
(二)局部应变法中的史密斯公式
疲劳失效是一个持续的、逐步积累的过程。叶轮每旋转一圈都会产生一次应力,应力集中的部位会逐渐形成微裂纹,最终导致其失效。
在众多理论中基于平均应力的分析方法是史密斯公式。史密斯学者以试验为依据,认为平均应力不光与弹性形变幅值有着内在的紧密联系,还与塑性形变幅值存在着千丝万缕的互相关联。经过大量论证性的试验分析,史密斯总结得出其理论是使用零件中存在的最大应力与总体应变幅值二者的乘积得出其损伤系数这一重要结论。
零件的疲劳破坏都是从应变集中部位的最大局部应变处开始,并且在裂纹萌生以前,都要产生一定的塑性变形,而局部塑性变形是疲勞裂纹萌生和扩展的先决条件。因此,决定零件疲劳寿命的是应变集中处的最大局部应变。本文考虑了实际作业中零件的表面加工与尺寸等因素对高周疲劳的影响,对以上综合因素进行总结后,进一步得出改进后的史密斯公式:
其中,为最大应力值;为局部应变幅值;为疲劳强度系数;为疲劳延性系数;E为材料的弹性模量;N为疲劳寿命;c为疲劳延性指数;为考虑了零件的表面加工与尺寸影响后的疲劳强度指数。
(三)叶轮疲劳寿命预测与计算程序
疲劳失效是叶轮发生破环的主要原因。通过对改进后的史密斯公式的化简,得到疲劳寿命N的计算式。化简过程如下:
考虑到公式中存在开n次方根的根,同时需多次进行对数求解,且需代入的参数非常多,因此本文通过Visual Basic语言编程环境,将以上的计算程序化,并作可视化窗口。将有限元分析的结果输入程序中,其计算结果如图6所示。根据计算结果,预测出叶轮的疲劳寿命为58074小时,近似1319397.79次应力循环次数。
四、发动机可靠性试验
增压器在发动机上的安装是一个必须引起重视的问题,因为它既影响增压发动机的动力性,又影响可靠性。在车辆上由于动力舱空间有限,还必须保证总体布置的紧凑性。增压器在发动机上的布置牵涉涡轮增压器、中冷器以及与之相连的进排气管的布置,即关系到整个增压系统的布置。本文中发动机为V型发动机,将涡轮增压器与中冷器安放在V型夹角的中间或上方。检查发动机,进行磨合后开始试验。
对试验数据进行采集,将相关数据绘制成曲线,发现叶轮在经过考核试验后无明显裂纹,满足实际使用要求。
本文通过对叶轮模型进行有限元分析,发现叶轮工作时高速旋转产生的离心力是其疲劳发生的主要诱因,并得出叶轮根部位置是应力集中的主要部位。基于局部应变法中低周疲劳对叶轮的影响,采用改进过的史密斯公式预测了叶轮的疲劳寿命循环次数,对今后的叶轮疲劳分析提供理论依据。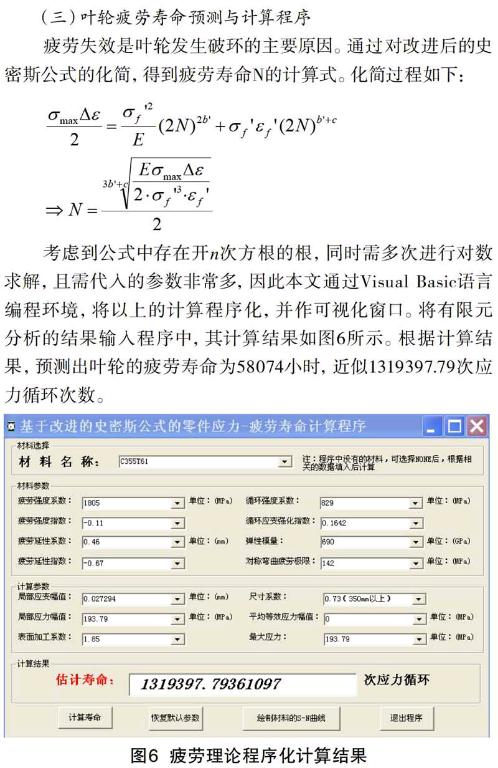
【参考文献】
[1]朱大鑫.涡轮增压与涡轮增压器[M].北京:机械工业出版社,1992
[2]徐娜,马朝臣.基于自循环方式的涡轮增压器疲劳寿命测试方法[C].昆明内燃机学会联合学术年会,2014(8)
[3]孟令广.车用涡轮增压器压气机叶轮低周疲劳研究[D].北京:北京理工大学硕士学位论文,2005
[4]裴月,薛飞,王荣桥.涡轮盘低周疲劳寿命可靠性研究[J].燃气涡轮试验与研究,2007(1)
[5]曾春华,邹十践.疲劳分析方法及应用[M].北京:国防工业出版社,1991
【作者简介】杨玲玲(1981— ),女,山东威海人,硕士,柳州铁道职业技术学院讲师,研究方向:汽车设计制造与检测维修。
