谈“奇数与偶数”的教学处理

文︳徐国强

谈“奇数与偶数”的教学处理

文︳徐国强

人教版小学数学五年级下册中有如下问题（如图所示）。该问题相对抽象，如何帮助学生理解和掌握相关结论？笔者在教学实践中总结了如下经验。

一、正确理解问题

题目是让我们研究奇数、偶数相加时，和可能存在的规律。但题目的这种设问的方式可能给人一种错觉。以“奇数与偶数的和是奇数还是偶数？”为例，它容易让我们认为答案要么是奇数，要么是偶数。尽管最终答案的确是奇数，但这是研究的结果。研究之前，我们应认识到，这一问题的答案有三种可能——或者是奇数，或者是偶数，或者不确定。若先入为主地认为答案要么是奇数，要么是偶数，将会使我们的说理变得浅尝辄止：既然正确答案或者是奇数，或者是偶数，我们只需用一个具体的例子试一下就行。比如，由1+2=3立即得到答案是奇数。如果正确理解了题目，我们面对1+2=3这个例子时，能得到的结论是：奇数加偶数，其和或者是奇数，或者不确定。

二、多角度说理

要真正理解上述结论，多角度说理是不可或缺的。常见的方式有如下几种。

1.不完全归纳。这是通过列举有限的例子得出结论的说理方式。比如，为了研究奇数与偶数的和的奇偶性，我们通过研究1+2，3+8，9+24等发现其结果均是奇数，从而得出结论：奇数+偶数＝奇数。用不完全归纳法得到结论后，要引导学生认识到这种方法的局限性：例是举不完的。我们通过对有限几个例子的考察，发现考察的对象都满足某一规律，其实并没有充分的理由确定所有的对象都满足这一规律。对这种方式的局限性的认识，是进一步考虑其他说理方式的基础。

2.以形说数。我们以图1中的图形表示奇数，用图2中的图形表示偶数。显然，一个表示奇数的图形和一个表示偶数的图形拼在一起，还是一个表示奇数的图形，从而得到“奇数+偶数＝奇数”。其他的情形类似。

3.运动变化。考虑一个人游泳，横渡一条小河。显然，他横渡小河一次到了对岸，再横渡一次，又回到了出发的地方。进一步，横渡小河奇数次，到了对岸，横渡小河偶数次，回到了出发的地方。考虑奇数+偶数，相当于先横渡奇数次，再横渡偶数次，即先到对岸，再横渡偶数次，显然还在对岸，相当于横渡奇数次。于是奇数+偶数＝奇数。考虑运动与变化还容易理解一个更一般的结论：由于在运动变化中，偶数往往意味着不变，因此，一个数加上偶数，不改变奇偶性。

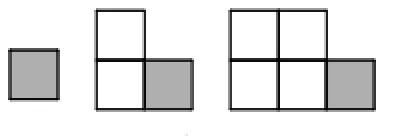
图1

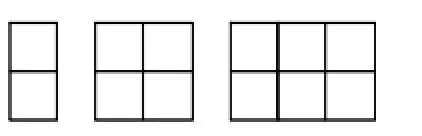
图2

三、联系与推广

1.加强联系。以下三个结论：奇数+奇数＝偶数，奇数+偶数＝奇数，偶数+偶数＝偶数，可以通过“奇数+1＝偶数，偶数+1＝奇数”建立起联系。比如，知道“偶数+偶数＝偶数”，那么，奇数+偶数＝偶数+1+偶数＝偶数+偶数+1＝偶数+1＝奇数，这就在“偶数+偶数＝偶数”与“奇数+偶数＝奇数”之间建立起了联系。其他的情形类似。

2.适当推广。推广的方向主要有两个，一是从两个到多个。得到奇数个奇数的和是奇数，偶数个奇数的和是偶数。进一步，在一个加法算式中，如果奇数的个数是奇数个，则和为奇数；如果奇数的个数为偶数个，则和为偶数。二是由加法推广到乘法。得到奇数×奇数＝奇数，奇数×偶数＝偶数，偶数×偶数＝偶数。进一步，在一个乘法算式中，只要存在偶数，结果就是偶数，否则，结果就是奇数。

（作者单位：宁乡县老粮仓镇中心小学）