以误为饵，点石成金

文︳朱天见

以误为饵，点石成金

文︳朱天见

俗话说“玉不琢不成器”。对于课堂教学来说亦是如此。学生有时会产生许多比较粗糙但又有价值的观点，就如正待雕琢的璞玉。教师要像能工巧匠，琢磨学生的语意，提炼学生的心意，才能达到点石成金的目的。数学具有高度的抽象性，学生完全接受有一定的困难，主要表现在对概念的理解肤浅，应用概念分析问题时常常依葫芦画瓢，容易产生错误。因此，教师在教学中要把握好学生学习的难点，有针对性地设计问题，促使学生独立思考、主动探究、合作交流，真正理解并掌握新知。

一位教师在教学长方体和正方体的表面积一课后，为了让学生切实把握知识的本质，出示了这样一道练习题：把2块棱长为1cm的正方体拼成一个长方体，求它的表面积。

生1（张口就答）：1块正方体的表面积是1× 1×6=6（cm2），2块正方体的表面积就是6×2=12（cm2）。（大部分学生点头表示同意）

生2（迟疑地）：他说的不对，将这两个正方体拼在一起，它们挨着的两个面重叠了，应该不算。

其他学生觉得生2的意见有道理，都认真思考起来：有的用学具摆，有的

在纸上画，还有的在议论。老

师也在黑板上画出图1、图2。

生1（不服气地）：你看，这两个面不还在中间吗，怎么可以不算？

生2：可是，长方体的表面积是指长方体6个面的总面积（边说边用手比划上下面、前后面、左右面），中间的两个面重合了，就不能算。

生1（不好意思地挠头）：哦，我没想到。（其他学生也都恍然大悟）

师：对呀！中间的2个面不能算。那2块正方体拼成的长方体表面积到底是多少呢？

生3：长方体表面积是：（2×1＋2×1＋1×1）×2=10（cm2）。

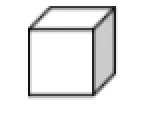
图1

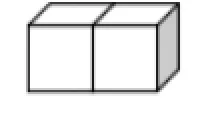
图2

生4：也可以直接用（12－2）×（1×1）=10（cm2），因为原来2块有12个面，拼起来后，中间2个面就消失了，剩下10个面，也就是10个1cm2，即10cm2。

师：那如果是用3块正方体这样拼起来呢？

由于有了前面的基础，学生纷纷动手画图、思考，很快得出（1×1）×（3×4＋2）=14（cm2）。

师：那如果把4块正方体排成一排拼起来呢？n块正方体排成一排拼起来，表面积又是多少呢？

学生经过计算和讨论，发现其中的规律：每次把左右两面单独看成2个面，1块正方体还有上下前后4个面，共有1×4＋2=6（个）面；2块正方体还有上下前后2×4个面，共有2×4＋2=10（个）面……n块正方体拼起来共有（4n＋2）个面。

以上教学片段中，学生之所以出现这样的错误，是因为他们对立体图形表面积的概念理解得不到位，这也是学生学习表面积知识必不可少的过程。只有经历了这样的过程，学生才能真正理解单一立体图形的表面积与组合立体图形的表面积之间的关系。这样的错误往往是学生思维的真实反映，蕴含着宝贵的亮点。案例中，教师让学生充分展示思维过程，探求其产生错误的内在因素，有针对性地展开教学，让学生对知识进行自主建构。有了这样的过程，学生对组合立体图形表面积的理解也更透彻。

学生的错误是课堂教学的宝贵资源，是正确的先导。在课堂上，教师不仅要宽容学生的错误，更要善于挖掘、利用，从错误中提炼有价值的问题，引导学生去探究、去交流，不断提高学生发现、分析、改正错误的能力，达到正确掌握知识、形成技能的目标。

（作者单位：浙江省义乌市香山小学教育集团）