非线性拟合LST/NDVI特征空间干湿边优于传统线性拟合方法的讨论

王行汉，丛沛桐，亢 庆，扶卿华，刘超群，王晓刚

（1. 华南农业大学水利与土木工程学院，广州 510610； 2. 珠江水利委员会珠江水利科学研究院，广州 510611；3. 水利部珠江河口动力学及伴生过程调控重点实验室，广州 510611）

·争鸣与讨论·

非线性拟合LST/NDVI特征空间干湿边优于传统线性拟合方法的讨论

王行汉1,2,3，丛沛桐1※，亢 庆2，扶卿华2，刘超群2，王晓刚2

（1. 华南农业大学水利与土木工程学院，广州 510610； 2. 珠江水利委员会珠江水利科学研究院，广州 510611；3. 水利部珠江河口动力学及伴生过程调控重点实验室，广州 510611）

地表温度/植被指数特征空间在土壤含水率、蒸散发等定量遥感反演和旱情监测、水资源管理方面有着重要的应用，但其特征空间中干湿边的拟合方式的研究目前还相对缺乏。该文以美国俄克拉荷马州为例，针对地表温度/植被指数特征空间干边和湿边的最优拟合方式展开研究，分别采用线性、指数、对数、多项式和幂函数对干边和湿边进行拟合，并采用16个土壤墒情站点的5、25和60 cm不同深度的3组实测土壤含水率数据对拟合结果进行评估。结果表明：对于干边的拟合，指数函数、线性函数、对数函数和幂函数拟合的决定系数r2分别为0.64，0.60，0.41，0.43，多项式函数拟合的r2最高（0.67）；对于湿边的拟合，指数函数、线性函数、对数函数和幂函数拟合的r2分别为0.59，0.63，0.67，0.69，多项式函数拟合的r2最高，为0.70；多项式函数拟合干边和湿边构建特征空间计算结果的均方根误差（RMSE，root mean square error）和平均绝对误差（MAE，mean absolute error）值均最小，在5、25和60 cm深度下RMSE分别为0.29、0.27和0.28，MAE分别为0.26、0.23和0.25，表明采用多项式函数拟合干边和湿边计算的结果精度最高且对25cm深度的土壤含水率最为敏感。

植被；温度；土壤水分；地表温度/植被指数；特征空间；干边；湿边

王行汉，丛沛桐，亢 庆，扶卿华，刘超群，王晓刚.非线性拟合 LST/NDVI特征空间干湿边优于传统线性拟合方法的讨论[J]. 农业工程学报，2017，33(11)：306－314. doi：10.11975/j.issn.1002-6819.2017.11.039 http://www.tcsae.org

Wang Xinghan, Cong Peitong, Kang Qing, Fu Qinghua, Liu Chaoqun, Wang Xiaogang. Discussion on method of nonlinear fitting dry and wet edges of LST/ NDVI feature space better than traditional linear fitting method [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(11): 306－314. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.11.039 http://www.tcsae.org

0 引 言

地表温度/植被指数特征空间是对象元的地表辐射温度和植被覆盖度的二维空间分布的一种解译[1]。三角形特征空间的概念是Price在研究区域尺度的蒸散发的过程中首次提出的[1-2]，当区域内植被覆盖和土壤干湿程度跨度范围较大时，遥感植被指数（vegetation index, VI）和地表温度（land surface temperature, LST）的散点图近似呈三角形分布，它包括2个极端的边界，一个是干边，代表水分严重亏缺，无水分可以用于蒸散；另一个是湿边，代表土壤水分充足，植被处于潜在蒸散状态。在早期的研究中，研究者发现遥感光谱植被指数和地表辐射温度之间有着很强的相关性[3-4]，借此用来对地表蒸散发和土壤含水率的研究，并进一步的提出了以地表温度/植被指数为代表的特征空间。特征空间方法依赖的基础理论为：1）遥感植被指数和地表温度之间有着强相关性[3-6]；2）在同等植被覆盖条件下，当作物受到水分胁迫时，叶片气孔自卫性关闭，减少了植被蒸腾作用，引起地表温度上升。不少学者对于地表温度/植被指数之间的关系进行了研究[7-13]，结果均表明其之间具有极强的负相关性[3-6]，并进一步的对地表温度/植被指数与空气气温[14]、土壤含水率[11,15]等之间的关系进行了研究，被广泛应用于蒸散发[16-17]、土壤含水率[11]、土壤盐渍化[18]、农作物生长[19]等参数的估算，对研究农业灌溉、干旱监测[20-23]、土地覆盖利用变化监测以及水资源管理与规划具有重要的意义。

利用特征空间估算蒸散发和土壤含水率的关键在于干边和湿边的确定，也就是获取充分供水及极端缺水条件下植被指数与地表温度的计算关系。过往的研究大体可以分为2种思路，一种是依赖于经验和先验知识，在干边上选择地表温度最大值[24-25]，在湿边上主要选择水体表面温度[26]、区域平均气温[27]或者地表温度最小值[24-25]。另一种思路是通过一定原理计算特征空间顶点的地表温度或者地表温度与大气温差[27-29]。对于特征空间的构建，其干边和湿边的确定尤为关键，但是目前对于干边和湿边拟合方式方面的研究还相对缺乏。在传统的地表温度/植被指数特征空间模型的构建当中，对于模型中的干边基本均采取了简单的线性负相关关系进行参数拟合，对于湿边认为与坐标轴平行的简化处理[11]。这样的处理是否恰当，精度如何是本文着重需要进行讨论的。

本文针对地表温度/植被指数特征空间干边和湿边的拟合方式展开研究，分别采用线性、指数、对数、多项式和幂函数对干边和湿边分别进行拟合，并结合美国西南部地区俄克拉荷马州的一块研究区，利用实测土壤含水率数据对拟合结果进行评估，以探讨和提高特征空间方法在大空间尺度上的适用性。

1 数据源和方法

1.1 研究区

本研究中选取美国俄克拉荷马州一块158 km× 147 km区域为研究对象，其中心位置为36°2′12.48″N、97°49′42.71″W，如图1所示。该区域内以平原为主，海拔在252～592 m之间。气候以干燥的温带大陆性气候为主，年平均气温为15.5 ℃，降雨量自东向西递减。森林覆盖率约为24%，主要分布在区域东部，研究区内的中北部主要为农业用地，植被覆盖度相对较低。

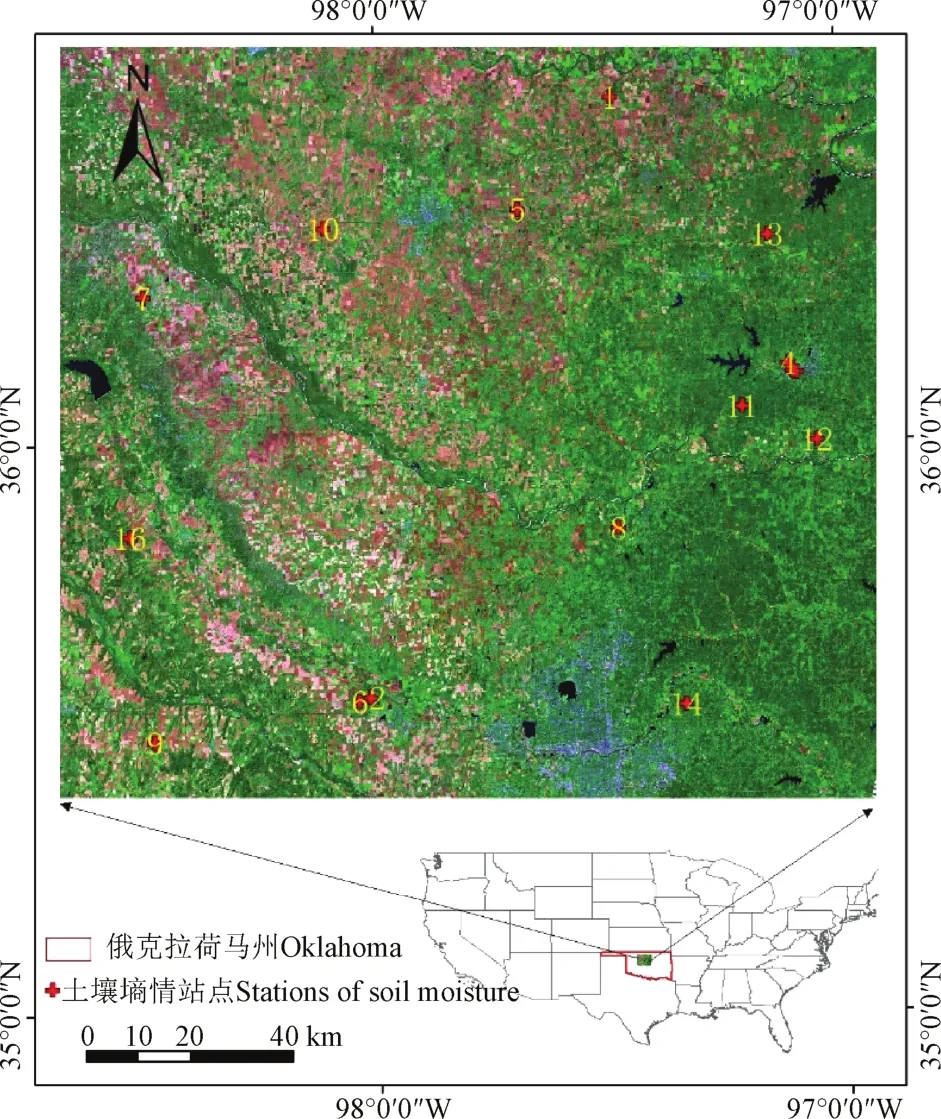
图1 研究区及土壤墒情站点分布图Fig.1 Location of study area and distribution of soil moisture stations

1.2 数据源

1）遥感数据

通过美国地质调查局（USGS）网站（http://glovis.usgs.gov/），下载获取研究区内Landsat TM5卫星数据，成像时间为2009年9月28日，影像质量为最佳等级，无云。Landsat TM5包含可见光-热红外多个光谱通道和热红外数据，空间分辨率为30 m，详细参数见表1。

表1 Landsat TM5遥感影像信息Table 1 Information of Landsat TM5 image

2）土壤墒情数据

土壤墒情数据来源于美国National integrated drought information system（https://www.drought.gov/drought/ soil-moisture-map），该系统包含了一系列深度的土壤含水率数据。在该研究区域内设有16个土壤墒情观测站（详细信息见表2），各站点的空间位置见图1。本文中使用5、25和60 cm共3种不同深度的土壤含水率数据对特征空间计算的结果进行分析。

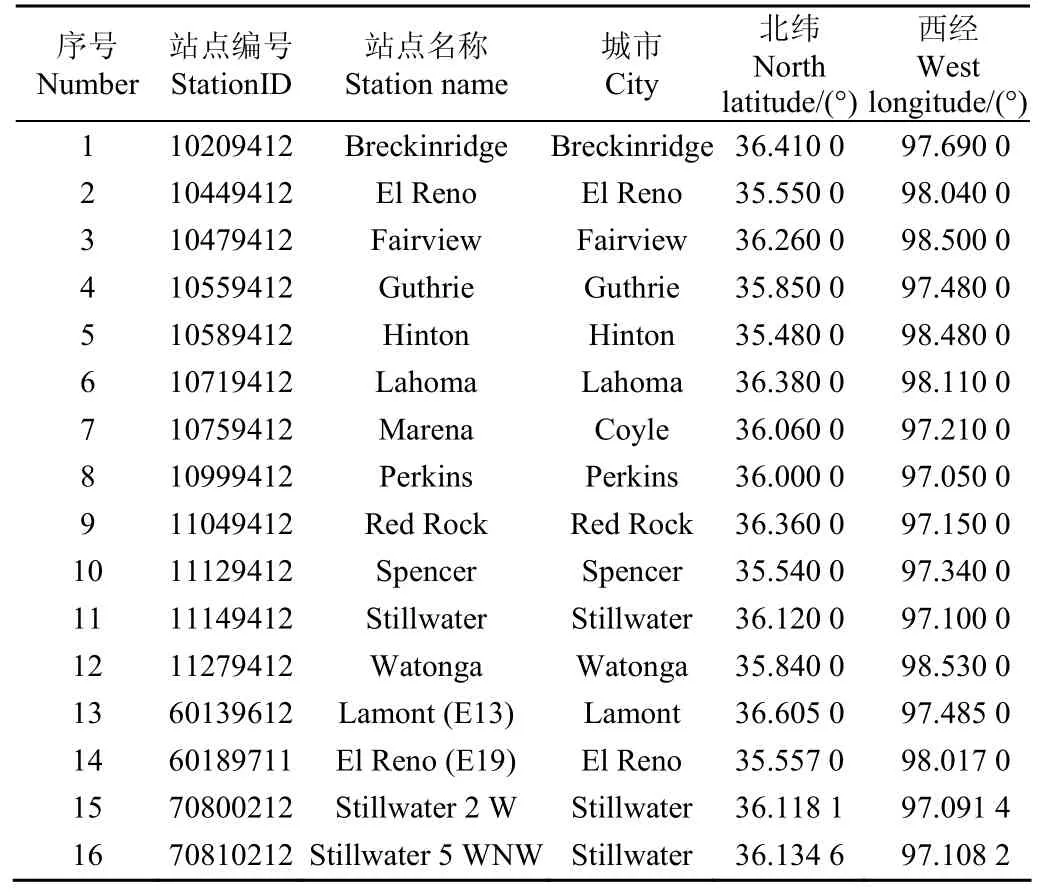
表2 土壤墒情站点信息Table 2 Information of soil moisture stations

3）土壤类型数据

土壤类型数据来源于联合国粮农组织（FAO）和维也纳国际应用系统研究所（IIASA）所构建的世界土壤数据库（Harmonized World Soil Database version 1.2）（http://webarchive.iiasa.ac.at/Research/LUC/External-Worldsoil-database）。通过查询，在该研究区内土壤类型单一，均为栗钙土（Kastanozems）。该土壤类型富含腐殖质，最初覆盖着早熟的原生草原植被，其深度在第1米内产生特征为棕色的表面层，具有与土壤颗粒结合相对高水平的可用钙离子，并且可以具有25～100 cm之间厚度的石炭蚀层。

1.3 归一化植被指数的计算

在本研究中，特征空间横坐标的植被指数的选取采用的是目前国际上使用最为广泛的植被指数——归一化植被指数（normailzed difference vegetation index, NDVI），它对于植被的生长和空间分布具有很好的指示作用，与植被覆盖度有很强的相关性[30-31]。其数学表达式为

式中ρNIR为近红外波段，ρRED为红光波段。NDVI理论值处于[-1,1]之间，负值表示地面覆盖为云、水、雪等类型，对可见光高反射；零值表示有岩石或裸土等类型，近红外波段光谱值和红波段光谱值近似相等；正值表示有植被覆盖，且随覆盖度增大而增大。但是由于受到地表湿度、太阳光照条件和大气条件等的影响，存在一些异常值，在本研究区域内负值主要为水体，在构建特征空间时对其进行了掩膜处理。

1.4 地表温度的计算

目前常用的地表温度的计算方法包括辐射传输方程算法、单通道算法和分裂窗算法，前人针对这3种计算方法开展了一系列研究[32]，结果表明辐射传输方程算法和分裂窗算法的精度相对较高，并且辐射传输方程算法的物理基础明确，反演精度较高。因此在本研究中选取了辐射传输方程算法反演地表温度，其原理是通过估计大气对地表热辐射的影响，并将大气对地表热辐射的影响从卫星传感器所观测到的热辐射总量中减去，得到地表热辐射强度，最后将热辐射强度转化为地表温度。地表温度LST计算的数学表达式为

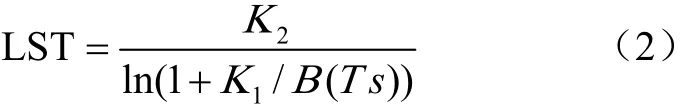
式中K1、K2为传感器的定标常数，B(Ts)指温度为Ts的黑体辐射亮度，B(Ts)计算的数学表达式为

式中Lλ为热红外辐射亮度值，ε为地表比辐射率，τ为大气在热红外波段的透过率，L↑大气向上辐射亮度，L↓大气向下辐射亮度。其中，大气在热红外波段的透过率、大气向上辐射亮度、大气向下辐射亮度可以在NASA官网（http://atmcorr.gsfc.nasa.gov/）中输入成影时间以及中心经纬度获得；地表比辐射率使用Sobrino等[33]提出的NDVI阈值法计算，数学表达式为

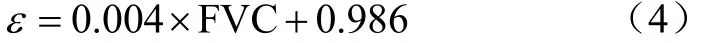
式中FVC是指植被覆盖度。对于植被覆盖度的计算采用的是基于NDVI的像元二分法模型[34-35]，计算数学表达式为

式中NDVIsoil指的是裸地像元值，NDVIvegetation指的是植被覆盖的像元值，目前常用的处理方式是根据整幅遥感影像上的NDVI的分布，以0.5%置信度[35]截取NDVI的上下阈值分别近似代表NDVIsoil和NDVIvegetation。

1.5 地表温度/植被指数特征空间构建及验证

地表温度/植被指数特征空间构建的核心是对干边和湿边的确定，传统的方法采用的是线性拟合，也就是用固定的NDVI间隔切割NDVI与LST的散点图，分别找到间隔内地表温度的最大值（LSTmax）和最小值（LSTmin），分别线性拟合NDVI值，得到干边和湿边。

本研究中采用同样的方法获取地表温度的最大值和最小值，但假定拟合方式为非线性关系（包括指数关系、线性关系、对数关系、多项式关系和幂函数关系，见图2），非线性拟合的数学表达式如下

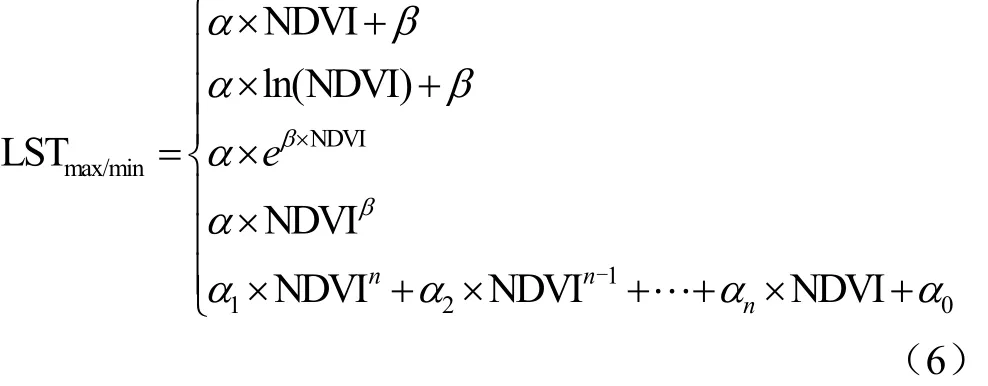
式中α和β代表干边和湿边拟合方程的拟合系数，n代表多项式的次数。

采用基于不同函数拟合方式构建的LST/NDVI特征空间，计算土壤含水率，数学表达式如下

LST/NDVI代表土壤含水率，为介于0~1之间的无量纲值，其值越接近1土壤含水率越低，越接近0其土壤含水率越高。

图2 地表温度/植被指数特征空间Fig.2 LST/NDVI feature space

为了评估不同函数拟合地表温度/植被指数特征空间计算结果的精度，本研究中采用决定系数r2、均方根误差（root mean square error, RMSE）和平均绝对误差（mean absolute error, MAE）作为评估的指标参数。均方根误差和平均绝对误差主要用来衡量观测值和模型值之间的偏差，能够很好地反映出模型计算的精确程度，其值越小，精确度越高[36]。数学表达式为

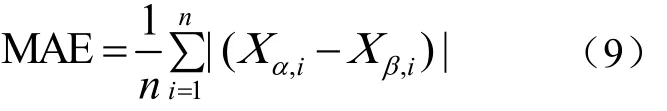
式中α,iΧ代表真实值，β,iΧ代表模型计算值，n代表真实值的个数。

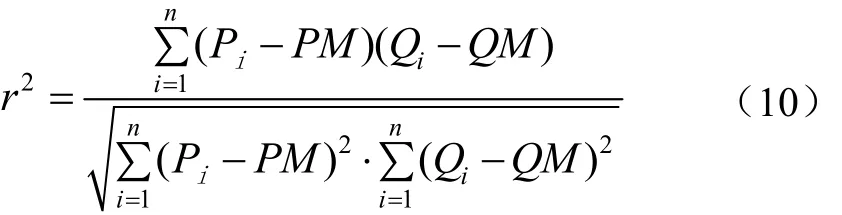
式中P和Q分别为实测值和估算值；PM和QM则分别为实测值和估算值的平均值；下标i代表n个实测值或者估算值中的第i个值。

2 结果与分析

2.1 NDVI与LST计算结果分析

NDVI和LST作为地表温度/植被指数特征空间构建的2个关键参数。其中，NDVI为特征空间的横坐标，LST为特征空间的纵坐标。在本研究中，利用Landsat TM5卫星遥感影像数据，经过大气校正、辐射定标等数据预处理后，结合公式（1）计算得到归一化植被指数NDVI，结合公式（2）－（5）计算得到地表温度LST，并借助于ENVI软件平台对其进行进行了统计，结果见图3和图4。

图3 归一化植被指数计算结果Fig.3 Calculation results of normalized differential vegetation index

由图3a可知，研究区内植被指数NDVI值空间分布存在较大差异，在中北部地区为农业用地集中分布区域，NDVI值主要集中在0.15左右，并且高植被指数与低植被指数呈现镶嵌式分布的特点；在东部地区主要为林草地覆盖区域，NDVI值主要集中在0.55左右。根据研究区内NDVI值统计曲线（图3b）可知，研究区内的NDVI值主要集中0.1～0.8之间，极大值和极小值的数量相对较少；并且NDVI值的数量在0.1～0.16和0.32～0.55两个区间内呈现不断增加的变化趋势，在0.16～0.32和0.55～0.9两个区间内呈现不断减少的变化趋势。上述结果表明了在整个研究区内体现了地表覆盖从裸土到稀疏植被再到茂密植被的变化过程，满足特征空间构建要求植被具有不同覆盖程度的要求。

由图4a可知，研究区东部地区LST值相对较低，主要集中在20～25 ℃之间，在中北部地区LST值相对较高，主要集中在25～35 ℃之间，并且25～30 ℃和30～35 ℃两个区间的LST值呈现镶嵌分布的特征。根据研究区内LST值统计曲线（图4b）可知，研究区内的LST值主要集中在20～35 ℃之间，而小于20 ℃和大于35 ℃的LST值的数量相对较少，并且LST值的变化范围较宽，能够满足特征空间的构建需要足够值域范围的地表温度变化区间的要求。

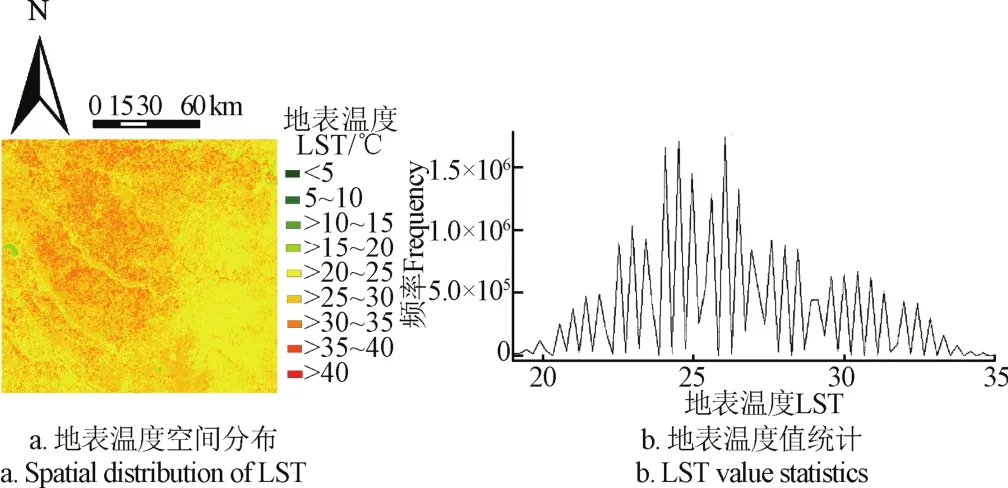
图4 地表温度计算结果Fig.4 Calculation results of land surface temperature

因此，计算得到的NDVI和LST能够满足构建地表温度/植被指数的要求，进一步的基于上述2个参数进行干边和湿边拟合。

2.2 干湿边拟合及LST/NDVI特征空间构建

基于ENVI软件平台，通过空间叠加分析，计算和统计NDVI对应地表温度的最大值和最小值，结果如图5所示。在干边上，即由最大地表温度组成的离散点，NDVI与LST呈现非线性关系，并且在NDVI为0.3～0.7区间内非线性特征关系表现尤为明显。在湿边上，即由最小地表温度组成的离散点，在NDVI介于0～0.8之间，LST随着NDVI的增加而增加，但超过0.8之后，LST值基本稳定，主要原因是在高植被覆盖区，当NDVI达到一定的值后发生了饱和的现象，这与王行汉等[37]研究的结果相一致。

图5 研究区内地表温度/植被指数特征空间构建Fig.5 Construction of LST/NDVI feature space in study area

根据上述构建的研究区内的LST/NDVI特征空间（图5），分别采用线性、多项式、对数、指数和幂5种函数方式对干边和湿边进行拟合，决定系数计算采用公式（10），结果见表3。

表3中5种不同函数拟合方式的决定系数r2介于0.4～0.7之间。对于干边，多项式函数的拟合效果最好，r2为0.67，其次是指数函数r2为0.64，对数函数和幂函数拟合效果相对较差，两者r2均不超过0.5。对于湿边，多项式拟合的效果最好，r2为0.7，幂函数次之，指数函数拟合效果最差。综合干边和湿边的拟合方式来看，多项式的拟合效果最好。

表3 干边和湿边5种函数拟合方程及其决定系数Table 3 Fitting equations of dry edge and wet edge and their determination coefficient of five functions

2.3 特征空间计算及验证分析

根据表3中线性、多项式、对数、指数和幂5种函数干边和湿边的拟合方程和地表温度/植被指数的计算方法（公式（6）、公式（7）），计算得到研究区内LST/NDVI值（图6），结果表明：

5种函数的拟合均能够体现出不同土壤含水率的空间分布，从宏观角度看整体空间分布规律存在一致性，土壤含水率较低的地区主要集中在研究区的中北部、中西部，土壤含水率相对较高的地区集中在研究区的东部地区。但对于具体计算结果值的表现上，5种函数又有所差别，指数函数的计算结果主要集中在0.5～0.6之间（图6a）；线性函数的计算结果主要集中在0.45～0.55之间，数据值的空间分布上与指数函数一致性较高（图6b）；对数函数的计算结果主要集中在0.55～0.6之间，在0.2～0.4区间内数值的空间突变性较指数函数、线性函数和幂函数更加突出（图6c）；幂函数的计算结果主要集中在0.6左右，0.2～0.6区间内数值变化呈现平缓上升趋势，无明显突变（图6d）；多项式函数的计算结果在0.2～0.8区间内的突变现象比较明显，并且数据结果主要集中在0.4～0.6之间（图6e）。由于研究区内中北部绝大部分地区为农业用地，高植被区与低植被区呈现镶嵌分布的特点，因此容易造成计算结果出现突变的现象，基于多项式函数的计算结果更加符合上述特征。

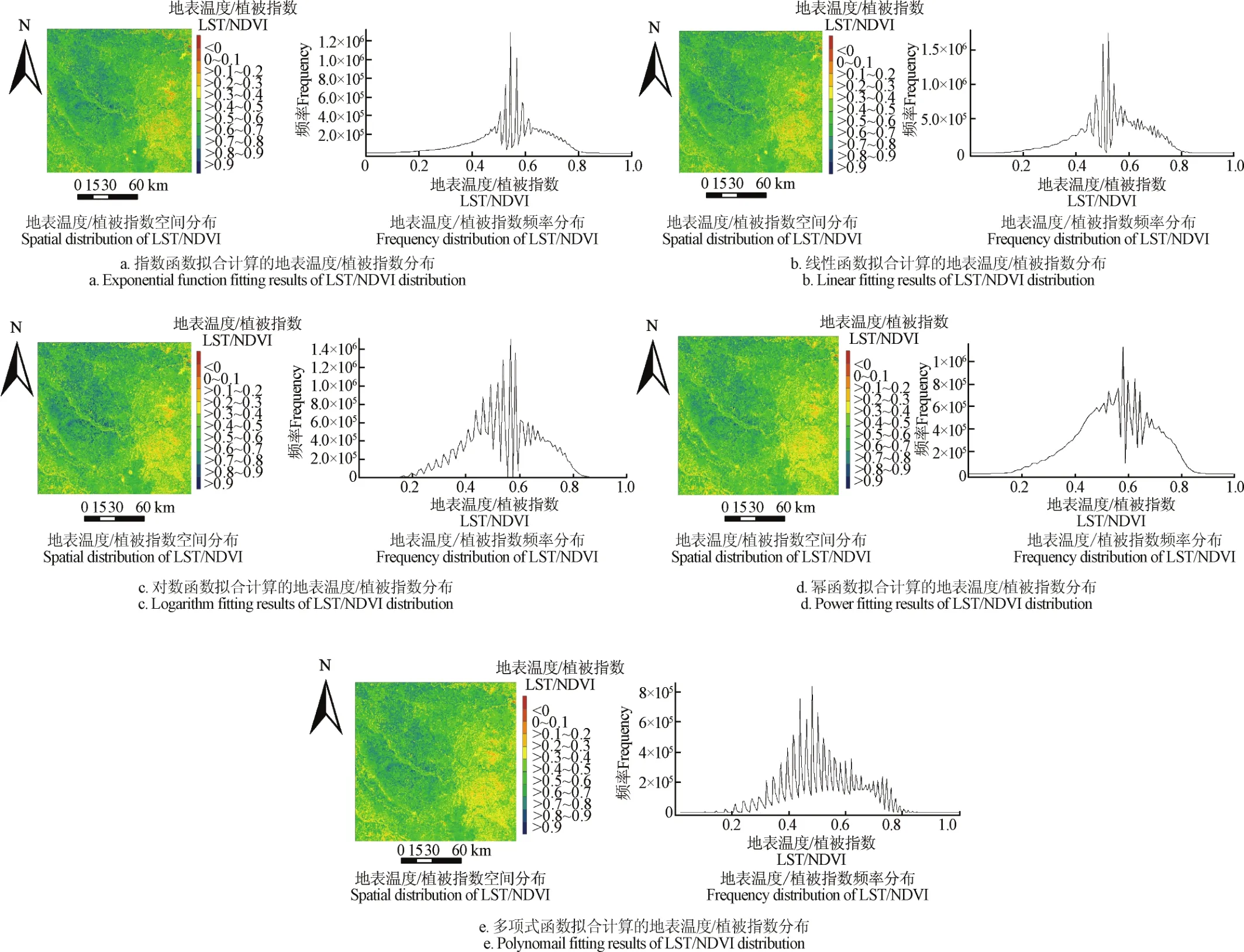
图6 研究区内5种函数拟合地表温度/植被指数计算结果Fig.6 LST/NDVI calculation results of five function fitting equations in study area

进一步为对比采用指数函数、线性函数、多项式函数、对数函数和幂函数分别拟合干边和湿边构建特征空间计算的LST/NDVI结果（图6），利用ArcGIS软件平台的空间分析模块提取16个土壤墒情站点对应的5种函数拟合干湿边计算的结果，并将该结果和土壤墒情站点的实测数据进行对比，并采用RMSE、MAE等指标参数对计算结果进行精度分析。

由于研究区内的土壤类型为栗钙土，土壤类型单一，因此可以不考虑不同土壤类型的影响。土壤墒情站点观测值为体积含水量，模型计算结果为相对含水量，在不考虑土壤质地等因素的影响，两者存在正比例关系，研究表明其之间存在一定相关性，因此可以作为精度评价的参考[11,20,22,38]。本研究中获取的16个土壤墒情站点的观测数据包含了5、25和60 cm 3种不同深度的土壤含水率值，通过利用土壤墒情站点不同深度的3组数据分别与5种函数拟合计算的结果进行对比，计算得到RMSE和MAE，结果见表4。

表4 不同深度土壤的5种函数拟合方式的均方根误差和平均绝对误差Table 4 Root mean square error and mean absolute error of five function fitting equations of different soil layers

根据表4可知，5种函数拟合的干边和湿边计算特征空间的结果精度存在一定的差异。由RMSE的结果可以看出：与5 cm深度的土壤含水率进行对比，多项式函数的RMSE值最小为0.29，其次是线性函数为0.31，对数函数为0.32，指数函数和幂函数最大；与25 cm深度的土壤含水率进行对比，多项式函数的RMSE值最小为0.27，其次是线性函数和对数函数，均为0.29，指数函数为0.30，幂函数最小为0.31；与60 cm深度的土壤含水率进行对比，多项式函数的RMSE值最小为0.28，其次是线性函数为0.30，对数函数为0.31，幂函数和指数函数最小，均为0.32。由MAE的结果可以看出：5种函数中，对于5、25和60 cm 3种不同深度，多项式函数的MAE值均为最小，分别是0.26、0.23和0.25，并且在25 cm土壤深度时取得最小值。

综合5、25和60 cm 3种土壤深度的RMSE和MAE值可以发现，5种函数中，多项式函数的RMSE和MAE在5、25和60 cm 3种土壤深度下的值均最小，表明采用多项式函数拟合干边和湿边计算的特征空间的结果精度最高，并且在25 cm深度时，RMSE和MAE值均为3组数据中的最小值，表明相对于5和60 cm土壤深度，特征空间计算的结果能够较好地反演该研究区内25 cm深度的土壤含水率。

3 讨 论

根据上述结果分析可知，在采用线性、指数、对数、多项式和幂5种函数对干边和湿边进行拟合的方式中，多项式函数的拟合效果最好，精度最高。根据表4中5种函数的RMSE和MAE值可以发现，采用多项式函数拟合计算的土壤含水率的精度较线性函数的计算结果有一定的提升。对于5 cm土壤深度，多项式函数的RMSE和MAE分别为0.29、0.26，线性函数分别为0.31、0.29；对于25 cm土壤深度，多项式函数的RMSE和MAE分别为0.27、0.23，线性函数分别为0.29、0.26；对于60 cm土壤深度，多项式函数的RMSE和MAE分别为0.28、0.25，线性函数分别为0.30、0.28；通过对比可以发现，对于3种不同土壤深度，多项式函数和线性函数之间RMSE和MAE差值较小，即误差整体相差较小，精度略有提升。在本研究案例中，采用线性函数和多项式函数分别对LST/NDVI特征空间中的干边和湿边拟合的决定系数r²差异较小（表3）。其中，线性函数拟合干边的r²为0.60，湿边r²为0.63；多项式函数拟合干边的r²为0.67，湿边r²为0.70。但并非所有的研究区域和研究时段，多项式函数和线性函数之间的差异均较小，根据王行汉等[39]的研究，在对于中国南方地区的研究中，采用线性函数拟合方式获取的干边方程拟合r²为0.946 4，湿边方程拟合r²为0.16；采用多项式函数拟合r²为0.998，湿边方程的拟合r²为0.970 5，通过对比，对于干边的拟合2种方法没有特别明显的差异r²基本处于0.9以上，但对于湿边的拟合2种方式差异较大，对模型计算的结果有较大影响。

因此，可以发现采用线性函数拟合干边和湿边方程的精度在不同的研究区域和不同的研究时间上存在一定的不确定性，从而对模型的计算结果造成一定的偏差。传统的模型构建中，一般采用线性函数的拟合方式获取干边和湿边方程，然而采用该方式趋势线可靠性无法得到保证，如果数据自身线性趋势性较好，拟合结果精度则较高；反之，如果数据自身线性趋势性较差，拟合结果精度则较低，其计算结果受数据自身影响较大，从而为计算结果带来一定的不确定性。

上述讨论表明，本论文研究提出的基于多项式函数拟合干边和湿边方程的方法相对于传统的线性函数的拟合方式稳定性强，过程关键步骤可控，对不同的研究区域和不同的研究时间均可保障模型计算结果的精确性，对提升该模型的适用性具有重要意义。

4 结 论

采用线性、多项式、对数、指数和幂函数5种不同函数分别对特征空间的干边和湿边进行了拟合，并结合土壤墒情观测站点数据对美国俄克拉荷马州进行了应用，结果表明：

1）特征空间中构建的干边，即最大地表温度组成的离散点，倾向于多项式分布，表现在多项式拟合的决定系数r2在5种拟合方式中最高，达到0.67；特征空间中构建的湿边，即最小地表温度组成的离散点，倾向于多项式分布，表现在多项式拟合的r2在5种拟合方式中最高，达到0.70。

2）通过5种函数对干边和湿边进行拟合，计算LST/NDVI特征空间值，并利用研究区内的16个土壤墒情站点5、25和60 cm不同深度的3组数据分别与5种函数拟合计算的结果进行对比，结果显示多项式拟合构建特征空间计算结果的均方根误差和平均绝对误差值均最小，表明采用多项式函数拟合干边和湿边计算的特征空间的结果精度最高，并且在25 cm深度时，RMSE和MAE值均为3组数据中的最小值，表明相对于5和60 cm土壤深度，特征空间计算的结果能够较好地反演该研究区内25 cm深度的土壤含水率。

[1] Price J C. Using spatial context in satellite data to infer regional scale evapotranspiration [J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28: 940－948.

[2] Carlson T N. An overview of the triangle method for estimating surface[J]. sensor, 2007, 7: 1612－1629.

[3] Goward S N, Cruickshanks G D, Hope A S. Observed relation between thermal emission and reflected spectral radiance of a complex vegetated landscape[J]. Remote Sensing of Environment, 1985, 18(2): 137－146.

[4] Nemani R R, Running S W. Estimation of regional surface resistance to evapotranspiration from NDVI and thermal-IR AVHRR data[J]. Journal of Applied meteorology, 1989, 28(4): 276－284.

[5] Goward S N, Hope A S. Evapotranspiration from combined reflected solar and emitted terrestrial radiation: Preliminary FIFE results from AVHRR data[J]. Advances in Space Research, 1989, 9(7): 239－249.

[6] Carlson T N, Perry E M, Schmugge T J. Remote estimation of soil moisture availability and fractional vegetation cover for agricultural fields[J]. Agricultural and Forest Meteorology, 1990, 52(1): 45－69.

[7] 田苗，王鹏新，孙威. 基于地表温度与植被指数特征空间反演地表参数的研究进展[J]. 地球科学进展，2010，25(7)：698－705. Tian Miao, Wang Pengxin, Sun Wei. A review of retrieving of land surface parameters using the land surface temperature-vegetation index feature space[J]. Advanceds in Earth Science, 2010, 25(7): 698－705. (in Chinese with English abstract)

[8] 杨曦，武建军，闫峰，等. 基于地表温度植被指数特征空间的区域土壤干湿状况[J]. 生态学报，2009，29(3)：1205－1216. Yang Xi, Wu Jianjun, Yan Feng, et al. Assessment of regional soil moisture status based on characteristics of surface temperature/vegetation index space[J]. Acta Ecologica Sinica, 2009, 29(3): 1205－1216. (in Chinese with English abstract)

[9] Gillies R, Kustas W, Humes K. A verification of the'triangle'method for obtaining surface soil water content and energy fluxes from remote measurements of the normalized difference vegetation index (NDVI) and surface[J]. International Journal of Remote Sensing, 1997, 18(15): 3145－3166.

[10] Boegh E, Soegaard H, Hanan N, et al. A remote sensing study of the NDVI–Ts relationship and the transpiration from sparse vegetation in the Sahel based on high-resolution satellite data[J]. Remote sensing of Environment, 1999, 69(3): 224－240.

[11] Sandholt I, Rasmussen K, Andersen J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status[J]. Remote Sensing of Environment, 2002, 79(2): 213－224.

[12] 于敏，高玉中，张洪玲. 地表温度-植被指数特征空间干旱监测方法的改进[J]. 农业工程学报，2010，26(9)：243－250. Yu Min, Gao Yuzhong, Zhang Hongling, et al. Improvement of Ts-NDVI space method in drought monitoring[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(9): 243－250. (in Chinese with English abstract)

[13] 李红军，郑力，雷玉平，等. 植被指数-地表温度特征空间研究及其在旱情监测中的应用[J]. 农业工程学报，2006，22(11)：170－174. Li Hongjun, Zheng Li, Lei Yuping, et al. Vegetation index-surface temperature feature space and its application in the regional drought monitoring[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(11): 170－174. (in Chinese with English abstract)

[14] Prihodko L, Goward S N. Estimation of air temperature from remotely sensed surface observations[J]. Remote Sensing of Environment, 1997, 60(3): 335－346.

[15] Otkin J A, Anderson M C, Hain C, et al. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought[J]. Agricultural and Forest Meteorology, 2016(218/219): 230－242.

[16] Stisen S, Sandholt I, Nrgaard A, et al. Combining the triangle method with thermal inertia to estimate regional evapotranspiration: Applied to MSG-SEVIRI data in the senegal river basin[J]. Remote Sensing of Environment, 2008, 112(3): 1242－1255.

[17] Minacapilli M, Consoli S, Vanella D, et al. A time domain triangle method approach to estimate actual evapotranspiration:Application in a mediterranean region using MODIS and MSG-SEVIRI products[J]. Remote Sensing of Environment, 2016, 174: 10－23.

[18] 王飞，丁建丽，伍漫春. 基于NDVI-SI 特征空间的土壤盐渍化遥感模型[J]. 农业工程学报，2010，26(8)：168－173. Wang Fei, Ding Jianli, Wu Manchun. Remote sensing monitoring models of soil salinization based on NDVI-SI feature space [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(8): 168－173. (in Chinese with English abstract)

[19] 刘云，孙丹峰，宇振荣，等. 基于NDVI-Ts特征空间的冬小麦水分诊断与长势监测[J]. 农业工程学报，2008，24(5)：147－151. Liu Yun, Sun Danfeng, Yu Zhenrong, et al. Water deficit diagnosis and growing condition monitoring of winter wheat based on NDVI-Ts feature space[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(5): 147－151. (in Chinese with English abstract)

[20] Zhao J, Xu J, Xie X, et al. Drought monitoring based on TIGGE and distributed hydrological model in Huaihe River Basin, China [J]. Sci Total Environ, 2016, 553: 358－365.

[21] Zhang T, Lin X. Assessing future drought impacts on yields based on historical irrigation reaction to drought for four major crops in Kansas[J]. Sci Total Environ, 2016, 550: 851－860.

[22] Mart nez-fernndez J, Gonz lez-zamora A, Snchez N, et al. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived soil water deficit index[J]. Remote Sensing of Environment, 2016, 177: 277－286.

[23] Assal T J, Anderson P J, Sibold J. Spatial and temporal trends of drought effects in a heterogeneous semi-arid forest ecosystem [J]. Forest Ecology and Management, 2016, 365: 137－151.

[24] Carlson T N, Gillies R R, Schmugge T J. An interpretation of methodologies for indirect measurement of soil water content[J]. Agricultural and Forest Meteorology, 1995, 77: 191－205.

[25] Jiang L, Islam S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations[J]. Geophysical Research Letters, 1999, 26: 2773－2776.

[26] Jiang L, Islam S, Guo W, et al. A satellite-based daily actual evapotranspiration estimation algorithm over South Florida[J]. Global and Planetary Change, 2009, 67(1): 62－77.

[27] Long D, Singh V P. A modified surface energy balance algorithm for land (M-SEBAL) based on a trapezoidal framework [J]. Water Resources Research, 2012, 48(2): doi:10.1029/2011WR010607.

[28] Moran M, Clarke T, Inoue Y, et al. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index[J]. Remote Sensing of Environment, 1994, 49(3): 246－263.

[29] Arnon K, Nurit A, Rachelt P, et al. Use of NDVI and land surface temperature for drought assessment: Merits and limitations[J].Journal of Climate, 2010, 23(3): 618－633.

[30] Liu Y, Mu X, Wang H, et al. A novel method for extracting green fractional vegetation cover from digital images[J]. Journal of Vegetation Science, 2012, 23(3): 406－418.

[31] Zhang X, Liao C, Li J, et al. Fractional vegetation cover estimation in arid and semi-arid environments using HJ-1 satellite hyperspectral data[J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 21: 506－512.

[32] 白洁，刘绍民，扈光. 针对 TM/ETM+ 遥感数据的地表温度反演与验证[J]. 农业工程学报，2008，24(9)：148－154. Bai Jie, Liu Shaomin, Hu Guang. Inversion and verification of land surface temperature with remote sensing TM/ETM+ data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(9): 148－154. (in Chinese with English abstract)

[33] Sobrino J A, Jim nez-mu oz J C, Paolini L. Land surface temperature retrieval from landsat tm 5[J]. Remote Sensing of Environment, 2004, 90(4): 434－440.

[34] Liu Y, Mu X, Wang H, et al. A novel method for extracting green fractional vegetation cover from digital images[J]. Journal of Vegetation Science, 2012, 23(3): 406－418.

[35] 穆少杰，李建龙，陈奕兆，等. 2001－2010 年内蒙古植被覆盖度时空变化特征[J]. 地理学报，2012，67(9)：1255－1268. Mu Shaojie, Li Jianlong, Chen Yizhao, et al. Spatial differences of variations of vegetation coverage in Inner Mongolia during 2001－2010[J]. Acta Geographica Sinica, 2012, 67(9): 1255－1268. (in Chinese with English abstract)

[36] Dennison P E, Roberts D A. Endmember selection for multiple endmember spectral mixture analysis using endmember average RMSE[J]. Remote Sensing of Environment, 2003, 87(2): 123－135.

[37] 王行汉，丛沛桐，刘超群，等. 2004－2013年珠江流域植被变化及其胁迫分析[J]. 生态学报，2017，37(19)，doi:10.5846/stxb201607111416. Wang Xinghan, Cong Peitong, Liu Chaoqun, et al. Analysis of vegetation variation and stress factors in the pearl river basin from 2004 to 2013[J]. Acta Ecologica Sinica, 2017, 37(19), doi:10.5846/stxb201607111416.

[38] Liu D, Mishra A K, Yu Z. Evaluating uncertainties in multi-layer soil moisture estimation with support vector machines and ensemble Kalman filtering[J]. Journal of Hydrology, 2016, 538: 243－255.

[39] 王行汉，亢庆，扶卿华，等. 一种农业旱情遥感监测方法：CN105929406A[P]. 2016-09-07.

Discussion on method of nonlinear fitting dry and wet edges of LST/ NDVI feature space better than traditional linear fitting method

Wang Xinghan1,2,3, Cong Peitong1※, Kang Qing2, Fu Qinghua2, Liu Chaoqun2, Wang Xiaogang2
(1. College of Water Conservancy and Civil Engineering, South China Agriculture University, Guangzhou 510610, China; 2. Pearl River Institute of Hydraulic Research, Pearl River Water Resources Commission,Ministry of Water Resources, Guangzhou 510611, China; 3. Key Laboratory of the Pearl River Estuarine Dynamics and Associated Process Regulation, Ministry of Water Resources, Guangzhou 510611, China)

Land surface temperature / vegetation index feature space has important applications in quantitative retrieval of water content in soil and crop evapotranspiration. However, at present, the research on the fitting of the dry and wet edges of the land surface temperature/vegetation index feature space was relatively lacking. In the tradition, for dry edge of the model, a simple linear negative correlation was adopted to fit the parameters, and wet edge was considered as a simplified treatment parallel to the coordinate axis. Whether it is appropriate is the focus of this paper that needs to be discussed. The study area was located in Oklahoma, the United States. Based on Landsat TM5 image data, land surface temperature (LST) and normalized difference vegetation index (NDVI) were calculated, and LST was calculated by radiation equation model and NDVI by pixel dichotomy model. And the fitting of dry edges and wet edges of LST/NDVI feature space was carried out with different functions, which included linear function, exponential function, logarithm function, power function and polynomial function. All of them were used to fit dry edges and wet edges respectively, and the results were evaluated by the measured data of water content in soil. The results showed that for the fitting of 5 different functions, r2value as a whole was between 0.4 and 0.7, and there were some differences in the fitting precision between different fitting methods. For the fitting of dry edges, r2value of exponential function fitting was 0.64, r2value of linear function fitting was 0.60, r2value of logarithm function fitting was 0.41, r2value of power function fitting was 0.43, and r2value of polynomial function fitting was 0.67 which was the best fitting way for dry edges. For the fitting of wet edges, r2value of exponential function fitting was 0.59, r2value of linear function fitting was 0.63, r2value of logarithm function fitting was 0.67, r2value of power function fitting was 0.69, and r2value of polynomial function fitting was 0.70 which was the best fitting way for wet edges. For the fitting of dry edges and wet edges, polynomial function was the best method. And the results of 5 kinds of function fitting were compared with those from the soil moisture stations in the study area. Root mean square error (RMSE) and mean absolute error (MAE) were calculated, and 5, 25 and 60 cm depth were selected. In the 3 different depths, RMSE and MAE of polynomial function were the smallest. RMSE at 5 cm depth was 0.29, RMSE at 25 cm depth was 0.27, and RMSE at 60 cm depth was 0.28; MAE at 5 cm depth was 0.26, MAE at 25 cm depth was 0.23, and MAE at 60 cm depth was 0.25. The results indicated that the LST/NDVI feature space inversion based on dry edges and wet edges fitting with the polynomial function was the most accurate for the soil surface water content in this study area, and it was most sensitive to water content at 25 cm depth in soil. For an optimal fitting, it must be an optimal solution between fitting accuracy and fitting efficiency. In the process of this study, only small amount of data were involved, so the main consideration was the accuracy of dry edges and wet edges fitting, not taking into account the time cost of computer computing process. But for the large amount of data operations in the actual application process, the time efficiency still needs to be considered.

vegetation; temperature; soil moisture; land surface temperature/vegetation index; feature space; dry edge; wet edge

10.11975/j.issn.1002-6819.2017.11.039

TP79

A

1002-6819(2017)-11-0306-09

2016-10-02

2017-05-04

广东省水利科技创新项目（2016-09）；广州市科技计划项目（201605030009）

王行汉，男，江苏东台人，工程师，博士生，主要从事植被遥感、水利遥感和农业旱情遥感监测。广州 华南农业大学水利与土木工程学院，510611。Email：rsgiswxh@126.com

※通信作者：丛沛桐，教授，博士生导师，主要研究方向为水利信息化与防灾减灾。广州 华南农业大学水利与土木工程学院，510610。

Email：congpeitong@126.com