虚拟计算环境的叠前深度偏移并行调度策略研究
2017-07-12梁宇轩韩君男
梁宇轩,祁 鑫,韩君男
(中国石油大学(华东) 计算机与通信工程学院,山东 青岛 266580)
虚拟计算环境的叠前深度偏移并行调度策略研究
梁宇轩,祁 鑫,韩君男
(中国石油大学(华东) 计算机与通信工程学院,山东 青岛 266580)
通过对地震资料处理数据进行分析,以模糊集合资源为依据,构建虚拟计算环境,并对并行任务进行有效划分,设计基于模糊聚类的并行调度算法。该算法首先对并行任务DAG图设计,然后采用模糊聚类方法将任务分配到合适的计算节点上,将资源在性能差异方面所产生的影响降到最低。研究结果证明计算节点分配任务的计算量越大,该节点的计算能力越强,表明这种方法可以最大限度的挖掘虚拟计算环境的能力,从而使成本变得更小,而效率得到提高。
虚拟计算;并行调度;模糊聚类
虚拟计算环境一般用来处理较大规模的数据计算任务,目的是利用计算环境组织异构资源协同工作来实现的,具体过程如下:首先是利用网络获取数量较多的空闲的计算资源;然后对计算资源存在的不同之处进行屏蔽;最后为各个用户分配合适的计算资源来协同工作[1-2]。地震资料处理在石油地质中有很重要的应用,是典型的大规模处理的异构环境[3],因此在对其建立的虚拟计算环境里[4],保证调度系统效率的关键所在,就是如何合理划分任务并提交到合适的节点。
1 异构环境下的并行任务划分
资源在虚拟计算环境下的基本特征是异构性,但是实际中计算性能的不同可能会造成调整策略的变动。本文研究的目的就是在虚拟计算环境中,能把地震资料叠前深度偏移数据划分到更合适虚拟计算环境,结合地震资料数据的特点以及地震资料处理的异构环境,提出了如下针对并行任务的划分算法。
(1)采用局部同构法将所有的资源分成n个梯度,通过二元组重新整合资源集合,即:
(1)
在式(1)中,有V和C两个集合,分别指的是资源性能和资源数量,所以Vi指在所有i(i=1,2,…,n)梯度时,资源的平均性能,Ci指在所有i(i=1,2,…,n)梯度的总和。由此可以得到最后梯度i(i=1,2,…,n)的计算能力为:Pi=ViCi,通过公式可以看出,某个梯度的计算能力是与这个梯度计算资源集合的最大任务计算量成正比的。
(2)依据不同个体的计算能力,进行任务的重新分配,用集合A={Ai|i=1,2,…,n}表示如下:
(2)
其中,Ai指的是最后要处理的炮集总数,nxshoti为炮集编号,梯度资源为i(i=1,2,…,n)。
(3)依据不同的梯度有着不同的任务量,计算炮数的起始和结束的数量,计算公式如下:
(a)当i=1时,
start_nxshoti=1,end_nxshoti=Pi.
(3)
(b)当i>1时,
(4)
其中,start_nxshoti和end_nxshoti分别指在整个数集里,不同梯度i(i=1,2,…,n)在所分得任务中的起始和结束的炮集编号,
(4)依据(3)中得到的各炮集数,获得起始和结束时刻的道数。
(5)
(5)对各个梯度内的任务进行二次划分。
如果Ci=1,则不需要此步骤,因为此时资源量为1。
2 基于模糊聚类的并行调度算法
2.1 并行任务DAG图设计
2.1.1 最短路径
通常情况下,在表示并行任务的DAG图里,为了能够的得到更短的执行总时间,所有的单独路径都要保证是最短的执行时间,所有的单独路径有一个相差不多的执行时间也很重要,即要保证均衡性。
依据以上两点,整个过程中每条执行路径都必须是性能最高且具有平衡性。如果整个过程中的单独路径数目为m,那么,其在x(x=1,2,…,m)的执行时间中,用区间[sx,ex]来表示,sx表示的起始时间,ex表示结束时间,这时整个系统的最高时效性与执行任务花费最长的时间路径息息相关,采用[smin,emax]表示最高时效性的调度目标,这其中:
(6)
由此得到了最短路径,也就是说在处理地震资料的过程中,对叠前深度偏移进行划分之后所得到的并行任务DAG图可以将复杂问题简单化,方便了整个调度策略的过程。
2.1.2 并行任务划分与执行时间
独立路径的数量是与并行划分后的子任务的数量相统一的,他们的起始点和结束点是一样的。调度过程的开始是在对DAG图第一层次进行任务划分和调度,这样保证了每条路径的起始时间点是一样的,此时刻设为0,得到如下公式:
smin=s1=s2=…=sm=0.
(7)
虽然在任务划分与调度层和并行执行层之间会有任务的传输开销,但其对整个过程的影响不大,这里将其忽略不计,这样在第二层时,同样认为他们的位置是起点时刻是同样的,所以整个过程就简单了,各个路径各自完成的最终执行时间可以看成三个部分的叠加,即:
(a)子任务在这条路径被并行执行所需要的计算时间;
(b)从得到这个任务的执行结果到其被送到所有结果进行叠加的节点上,这一过程需要的时间;
(c)最后所有结果被叠加,所用到的时间。
由以上的分析可知,一个并行子任务的数据规模决定这个子任务的执行时间,假设在传输数据量一样的情况下,那么传输的网络带宽就决定了需要花费的时间,在最后的结果叠加中,由此就得到了并行任务划分。
2.2 基于模糊聚类的并行调度算法
根据以上描述的调度目标,对模糊聚类的并行任务调度算法的详细表述如下:
(1)首先聚合资源节点,利用注册和信息服务,以模糊聚类方法为基础,从而得出一系列具有不同梯度的集合;
(2)得到整个梯度集合的计算能力,计算能力为梯度数量、节点数量、梯度负载等,并对优先级进行排序;
(3)将原始任务,根据其数据规模,设定其期望执行时间,任务期望的计算能力。再定义两个变量,分别为目标起始梯度和目标梯度范围;
(4)根据优先级降序,对梯度进行循环;
(5)遍历选择最合适的梯度,避免浪费,选择最合适的梯度,不需要进行跨梯度划分时,按照同构环境下的并行任务划分算法,将任务划分并调度到梯度,否则按照异构环境下的并行任务划分算法;
(6)做好任务划分和调度之后,还需要再找到另外一个可以成为结果叠加的汇总结点,这个节点可以指定之前的一个调度节点。
从以上的描述中,可以看出在各个资源虚拟计算环境里存在着微小的差别,因此在同构环境中简单化了调度算法,这样如果并行速度足够快,那么这个理论可以应用于实际中。在对资源节点的计算能力考虑时,要考虑两方面,一是其自身的静态物理属性,二是其当前的所有负载值,这样才能保证在调度过程中不会有大的偏差。综合来看算法的整个过程,如果不要求跨度调度,那么该算法可以达到理想情况;当必须要进行跨梯度划分调度时,该算法的最坏时间复杂度只有O(n2),所以可以看到这个算法与传统的DAG任务调度中的更加简单。
3 实验测试与结果分析
以叠前深度偏移应用实例进行了测试,第一步的测试分析过程针对的是原始任务串行的执行情况;第二步的测试过程针对的是按记录道数和按偏移道数两种不同方式任务进行分类。
3.1 具体应用案例
这是关于某个Fourier有限差分叠前深度偏移的应用案例,其中最重要的计算内容是素因子快速Fourier变换,主要输出来自于相关的数据体记录文件以及速度模型文件,最后的结果用偏移剖面图表示,下面是具体的表述:
记录数据:mar_ibm_1.sgy,240炮、23040道;
执行程序:sumigpreffd_sun.c,二维Fourier有限差分叠前深度偏移;
速度模型:mar_v_sun_sc_nh.sgy,249*750;
输出结果:myffd.dat;
3.2 并行任务的模糊聚类的并行调度算法测试
在并行划分和调度叠前深度偏移任务中,对处理器、内存、硬盘和网络通信四部分的按一定比例来分配,其集合为:
W={0.7,0.05,0.05,0.2}.
在整个过程中,以偏移道数模糊聚类为依据,按照记录道数和偏移道数两种不同分类的并行调度算法,执行叠前深度偏移测试。对试验结果分析后,选取合适的节点计算规模和合理的并行调度划分方式,节点选用的是2、4、8三个,对应的划分进程也为2、4、8。表1为最终执行时间的统计。 由上述结果可知,两种分类下的变化规律并不相同。按记录道数任务划分时,在节点数成倍上涨的情况下,其数据显示并不会出现执行时间的成倍减少,但按偏移道数任务划分时,在节点数成倍上涨的情况下,其数据显示执行时间基本也在成倍减少。这个原因是采用了按偏移道数的并行任务划分方法,这种分类方法,可以与叠前深度偏移的特性相适应,最后的工作时间也更短。
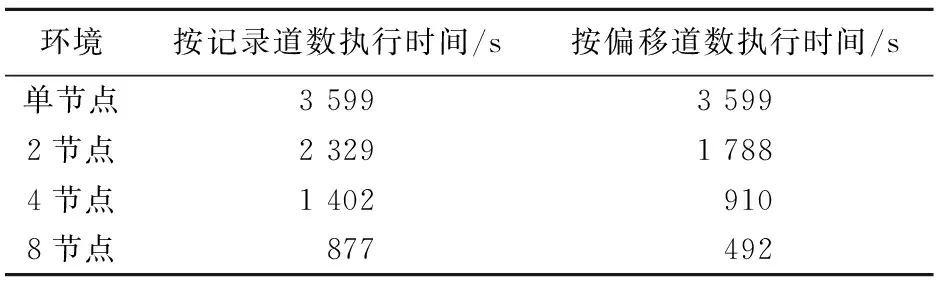
表1 两种分类所需时间的对比
4 结 论
(1)采用局部同构法将所有的资源分成n个梯度,通过二元组重新整合资源,对地震资料数据按照任务梯度进行并行任务划分,依据梯度计算炮数的起始和结束时刻的数量,实现了地震资料处理在虚拟计算环境下的任务划分。
(2)对已经划分好的叠前深度偏移并行任务进行DAG分析,得到最短路径,简化了并行任务,然后以偏移道数模糊聚类为依据,采用按偏移道数的并行任务划分方法,可以与叠前深度偏移的特性相适应,缩短了工作时间,提高了执行效率。
[1] 李伟,顾乃杰,刘振宽.三维叠前kirchhoff深度偏移软件在并行计算机上的实现技术[J].计算机工程与应用,2002(20):211-214.
[2] 张军华,仝兆岐,何潮观,等.基于HPF的地震资料并行处理系统研究与实现[J].计算机应用,2002,22(9):57-59.
[3] 马琳,陈莉.基于动态Profiling技术的流水粒度调优[J].计算机研究与发展,2005(6):163-170.
[4] 张辰,夏士雄,刘兵.一种改进的可能模糊聚类算法[J].计算机应用研究,2011,28(8):2849-2851.
[责任编辑] 董大伟
2017-03-15
国家自然科学基金项目(61671482)
梁宇轩(1996—)男,山东东营人,中国石油大学(华东)计算机与通信工程学院硕士研究生,主要从事高性能计算研究。
10.3969/j.issn.1673-5935.2017.02.012
TP338
A
1673-5935(2017)02- 0042- 03
