模糊数学在海(咸)水入侵水质评价中的应用——以寿光地区为例

付恩光,吴光伟，李同心

(1.寿光市国土资源局，山东 寿光 262700；2.山东省地质环境监测总站，山东 济南 250014；3.山东省地图院，山东 济南 250014)



模糊数学在海(咸)水入侵水质评价中的应用
——以寿光地区为例

付恩光1,吴光伟2，李同心3

(1.寿光市国土资源局，山东 寿光 262700；2.山东省地质环境监测总站，山东 济南 250014；3.山东省地图院，山东 济南 250014)

运用模糊数学的基本思想方法, 结合海(咸)水入侵的特点, 依据寿光地区2015年丰水期地下水水质监测结果,选取Cl-、矿化度、咸化系数、钠吸附比等4项水化学指标作为评价因子，构建模糊综合评价数学模型，对寿光海(咸)水入侵现状进行了模糊综合评价，并验证了此模糊综合评价结果的可靠性。

海(咸)水入侵;模糊数学;水质评价;综合评价；寿光地区

海(咸)水入侵是指由于陆地淡水位下降而引起的海(咸)水直接侵染地下淡水层的一种环境地质恶化现象，是自然和社会环境中诸多因素长期共同作用的结果。海(咸)水入侵已造成自然环境恶化，工业用水短缺，农业减产等危害，严重影响了入侵区经济的可持续发展[1-2]。由于地下淡水的过量开采，寿光市海(咸)水和地下淡水的过渡带向内陆侵染渐变，其边界具有模糊性和不易定量性。而模糊集合是对这些模糊现象或模糊概念的刻划[3],模糊综合评价是处理这类问题的理想方式。该文依据寿光海(咸)水入侵的性质和特点，运用模糊综合评价方法，对区内海(咸)水入侵进行了评价，并确定了区内海(咸)水入侵的锋线位置。

1 区域地质背景

寿光市位于山东省潍坊市西北部，属暖温带半湿润季风区，多年平均降水量605.8mm，降水的年际变化和年内变化极为悬殊。区内地势南高北低，较为平坦。南部、中部由冲积—洪积平原组成，堆积物由粘质砂土、砂质粘土、粉砂及粗砂等组成。北部沿海由滨海冲积—海积平原组成。堆积物由粉砂、粘质砂土和砂质粘土组成。该区属华北平原东缘，大地构造属胶莱地堑北段[4]。区内地下水类型以孔隙水为主，由于受地形地貌、古地理环境及人为因素的控制，地下水分布较为复杂。根据地下水水化学特征、含水层结构和成因，分为3个水质结构区。

(1)南部全淡区：位于区域南部，河流冲积—洪积平原的中上部，含水层由粗砂及中细砂组成，富水性强，径流通畅，水化学类型以HCO3-Ca(Ca·Mg)型水为主，矿化度小于1000mg/L。

(2)中部淡咸水过渡区，位于冲洪积平原前缘与滨海平原交接地带，含水层岩性以中砂、粉细砂为主，地下水径流条件差，补给条件较弱。在垂向上含水层呈犬牙交错状，由于咸水体向淡水体楔入，将淡水层分成浅层和深层两部分，咸水体顶底板呈喇叭状向北展布[5-6]。

(3)北部全咸区，位于滨海平原，含水层由粉细砂、中细砂组成，呈上细下粗的二元相结构特点。水化学类型Cl-Na。沿海岸地带宽度15～20km范围内，含有丰富的地下卤水，分3层赋存于松散沉积物中[7]。区内古河道密布，构成了海(咸)水入侵的优势通道。晚更新世以来，沧州、献县、黄骅3次海侵，南侧最大界线至寿光—寒桥—昌邑一带，在区内形成了3套海陆相地层相互叠置，与区内古海水的赋存及咸水入侵有密切关系[8]。

2 海(咸)水入侵模糊数学综合评价

模糊综合评价是以模糊数学方法为基础,将一些边界不清,不易定量化的因素定量化。根据模糊数学的基本原理,将该次综合评判归纳为以下几个步骤:①选取评价指标；②建立评价(判据集)集；③建立模糊关系评价矩阵；④确定评价因子权重；⑤计算评价指标；⑥归一化处理[9-10]。

2.1 评价指标选取

对海(咸)水入侵的模糊综合评价研究中,国内外尚存在诸多不同的指标体系。地下水化学特征是判断海(咸)水入侵的直接依据,选用合适的评价指标，对评价海(咸)水入侵及入侵程度至关重要。该次结合寿光地区水文地质特征，选取Cl-、矿化度、咸化系数、钠吸附比4项水化学指标作为评价因子。

Cl-在地下水中广泛分布，其溶解度大，不易沉淀析出，是地下水中最稳定的离子,海水中最主要的稳定常量元素，反映海(咸)水入侵最为敏感，测定也十分简便,因此将其作为首选指标[11]。

矿化度(M)反应的是地下水中的总盐量水平,基于海(咸)水和淡水在矿化度上具有的明显差异性,因此将其作为评价指标[11]；

Na+是海(咸)水中首要阳离子，其含量比淡水高出2～4个数量级。Ca2+，Mg2+是区域地下淡水的主要阳离子。受海(咸)水侵染的地下水中，Na+含量升高，超过一定限度，则会导致土壤次生碱化。选用钠吸附比(SAR)为海(咸)水入侵判断指标，既可以从咸—淡水中主要阳离子比值角度判断海(咸)水入侵程度，又可以从土壤环境化学方面考察海(咸)水侵染的影响[12]，因此将SAR作为评价指标。其表达式为[13]：

式中：c为括号内单元的浓度(mol/L)。

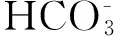
式中：c为括号内单元的浓度(mol/L)。

2.2 建立评价集

参照《地下水质量标准》(GB/T14848-1993)，根据寿光地区地下水水质特点及实际监测情况，结合相关的专业研究，考虑到海(咸)水入侵本身界线具有模糊性的特点，对其过渡带加以细化，突出反映海(咸)水入侵前缘的变化。据此，将海(咸)水入侵程度划分为3个级别(表1)，通常所说的海(咸)水入侵锋线处于Ⅰ级和Ⅱ级之间[14]。

表1 寿光地区海(咸)水入侵程度等级划分

根据海(咸)水入侵区地下水水化学特征,对选用的4项评价因子同时使用3级评价标准。结合相关的水质标准,参考已有的海(咸)水入侵等级划分,具体指标评价等级范围及代表值如表2所示。

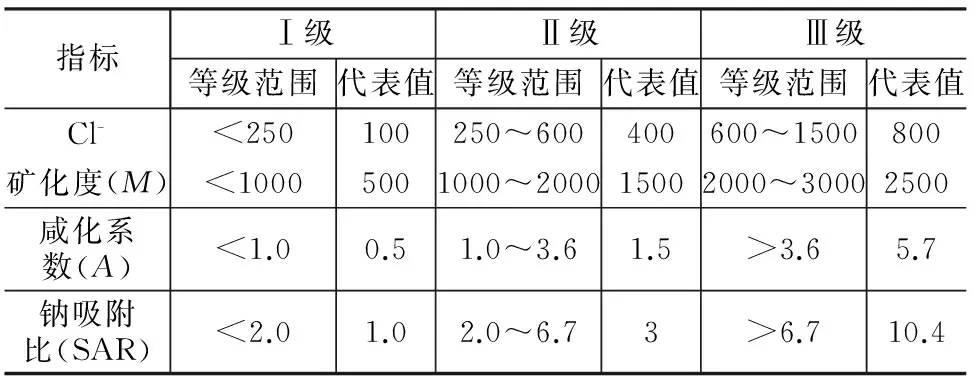
表2 寿光地区海(咸)水入侵具体指标

2.3 海水入侵模糊关系矩阵

对每一个水质监测点，建立各评价因子对应寿光地区海(咸)水入侵程度等级的隶属函数U，U为矩阵R的隶属函数，i(i=1，2，3，4)为评价因子的隶属度，按式(1)～(3)计算，求出隶属矩阵R[15-16]。

(1)

(2)

(3)

式中：U1i,U2i,U3i为i评价因子对Ⅰ～Ⅲ级质量标准(表2)的隶属度;Xi为i评价因子的实测值；a1,a2,a3,a4为i评价因子对应3级的代表值(表2)；计算所得隶属矩阵R为一个4×3的矩阵。

2.4 确定评价因子权重

指标权重是表示各单项指标在决定该评价点水质上所起的比重。由于各单项评价因子在指标权重上存在差别，且对评价点水质的贡献度也不同，因此需要对每个评价点各单项指标的权重进行分别计算，i(i=1，2，3，4)评价因子的指标权重计算如下：

(4)

(5)

2.5 计算评价指标

根据计算得出的权重模糊矩阵和各评价因子的隶属矩阵，对各评价点进行加权和合成，按公式(6)求得各评价点所属各级别的综合矩阵B。利用矩阵B中的数值大小，判断海(咸)水入侵程度等级。

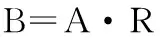
(6)

由式(6)求得的综合矩阵B是个1×4的矩阵，将其进行归一化处理，然后把综合矩阵B数值量化，得模糊评价集，则海(咸)水入侵的等级即为此评价集中的最大数值。

2.6 归一化处理

根据熊德国，鲜学福等人对模糊数学方法的改进，再对综合矩阵B进行归一化处理，以bi的下标作为量化指标[16]：

(7)

式中：H表示对评价集进行重新量化的一个指标；bi表示综合矩阵B的第i列。因B是归一化的结果，所以在式(7)就有1≦H≦3。这样，根据H的数值就可以判断该评价点海(咸)水入侵的级别，即H值最接近1～3数值中的哪个，就属于哪一级别。

2.7 在寿光海(咸)水入侵评价中的应用

2.7.1 水质资料统计

该次评价所选用的数据资料来源于山东省地质环境监测总站和寿光市国土资源局联合开展的“山东省寿光市海(咸)水入侵调查与自动化监测技术研究”项目2015年度丰水期水质监测成果。监测点的布设是依托前期工作成果，在历史海(咸)水入侵锋线两侧布设的。布设原则是垂直于历史入侵锋线，在西部的台头镇，中部的田柳镇和东部的候镇布设3条监测剖面29个监测点(图1、表3)。

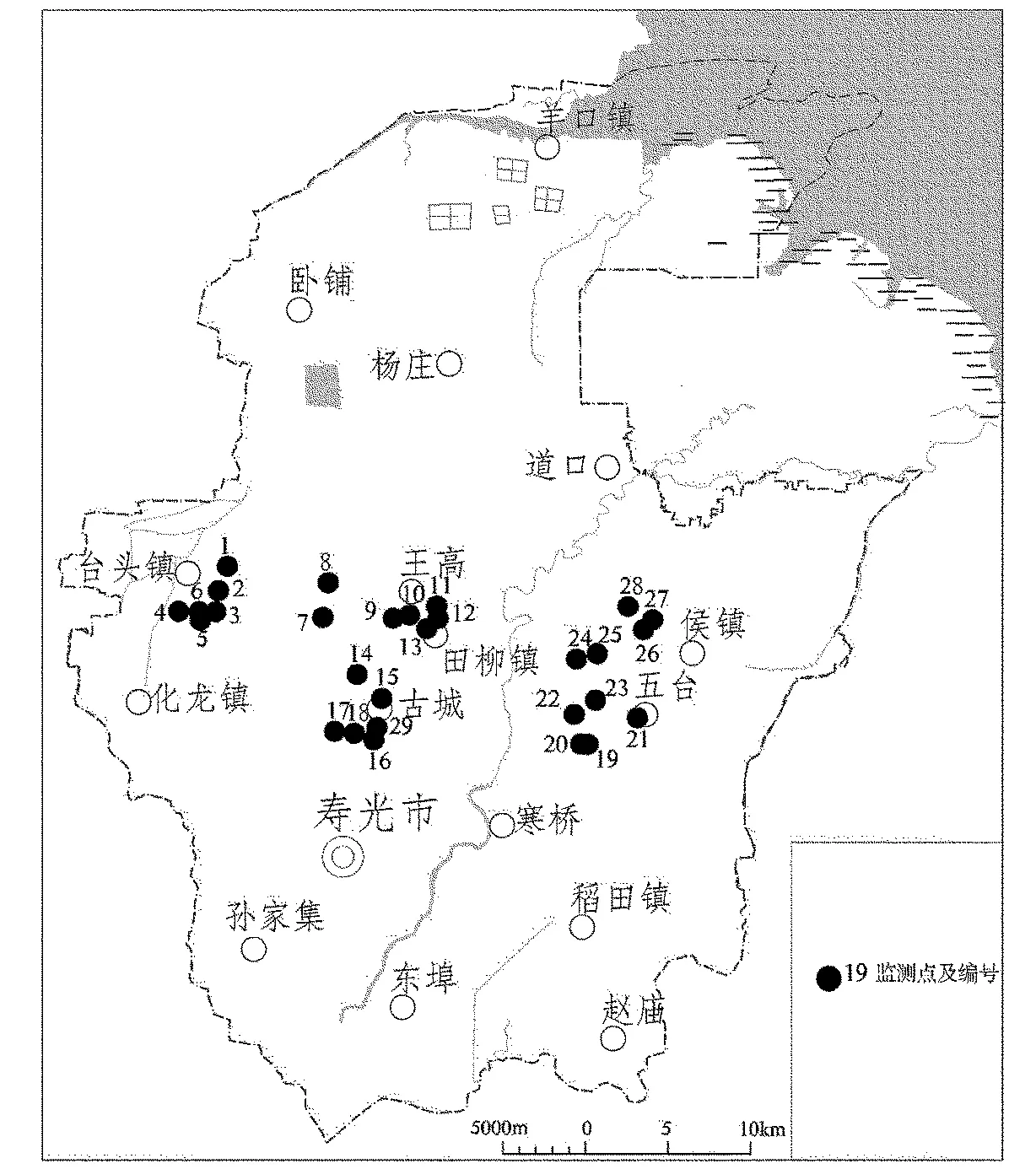
图1 地下水监测点分布图

2.7.2 模糊综合评价

对各监测点按照上述步骤进行模糊综合评价，最后得出各评价点的海(咸)水入侵等级(表4)，入侵级别Ⅰ级点20处，Ⅱ级点9处。

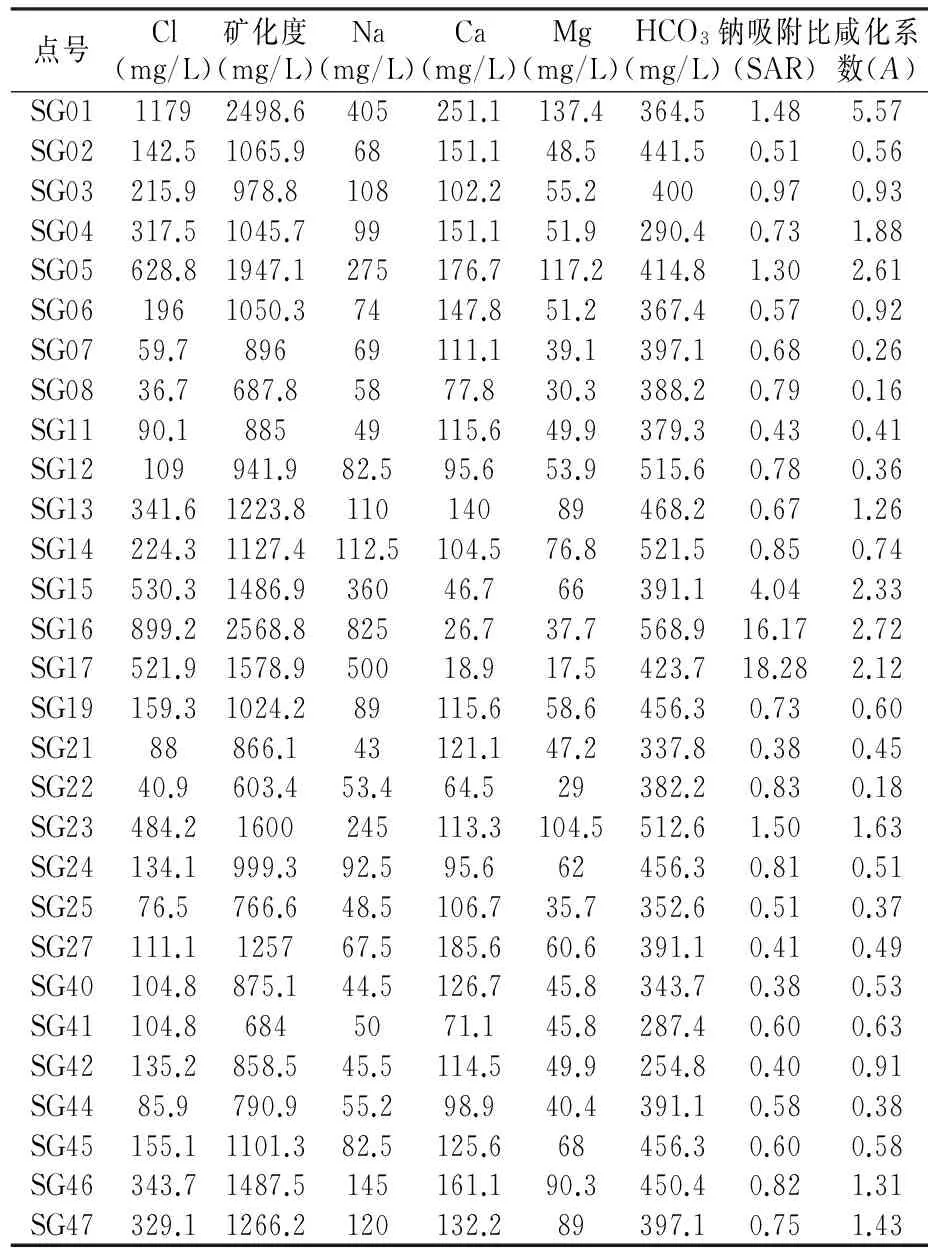
表3 寿光市海(咸)水入侵监测点水质(2015年丰水期)

表4 寿光海(咸)水入侵模糊综合评价结果

2.8 结果分析与应用

根据模糊综合评价结果，绘制2015年寿光市海(咸)水入侵综合评价锋线分布图(图2)，可以看出，海(咸)水入侵锋线沿寿光市台头—田柳—上口—五台一线分布，入侵线呈弧形曲线延伸。经和历年入侵锋线对比分析(图3)，较为符合真实情况。

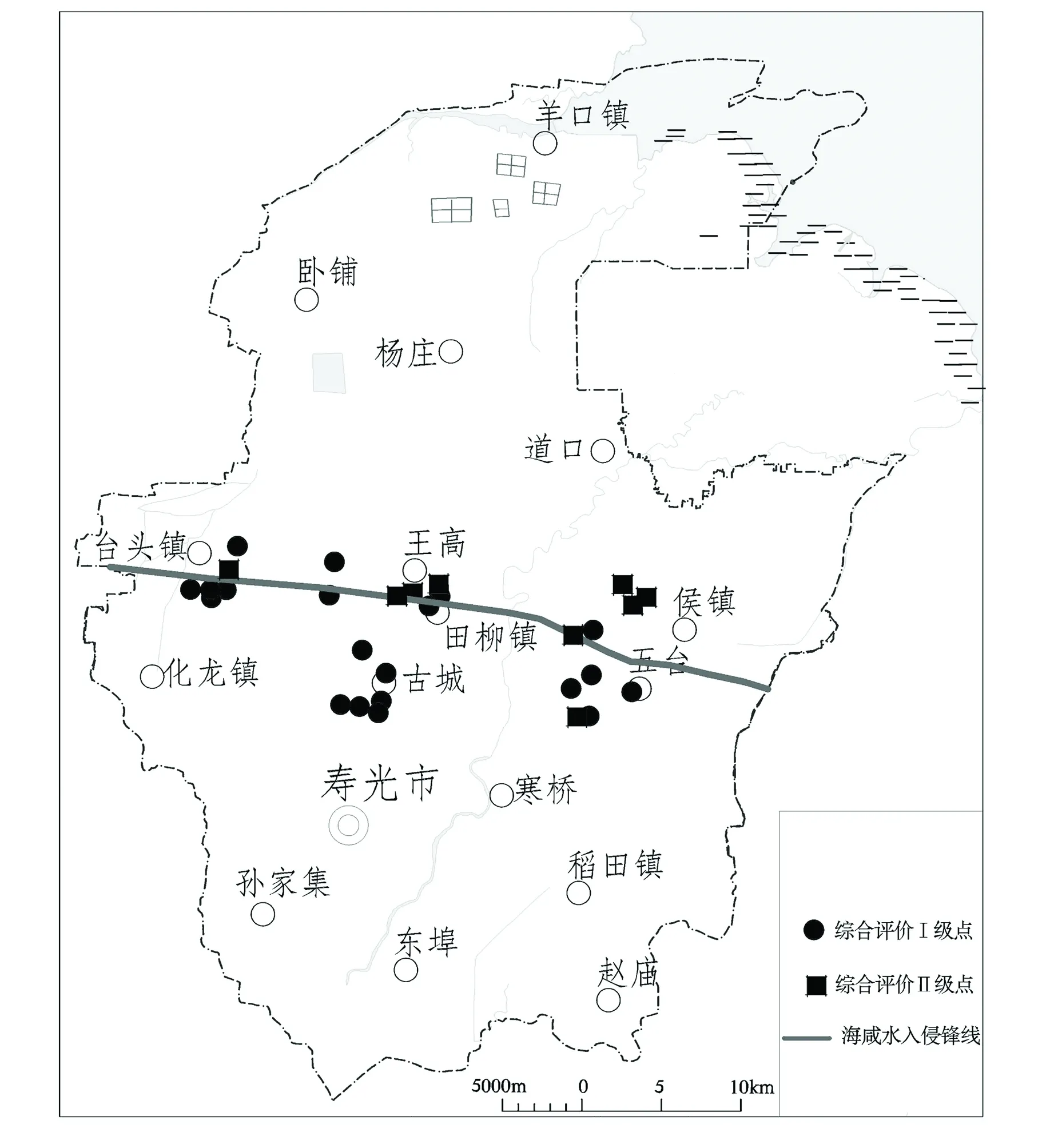
图2 综合评价入侵锋线分布图

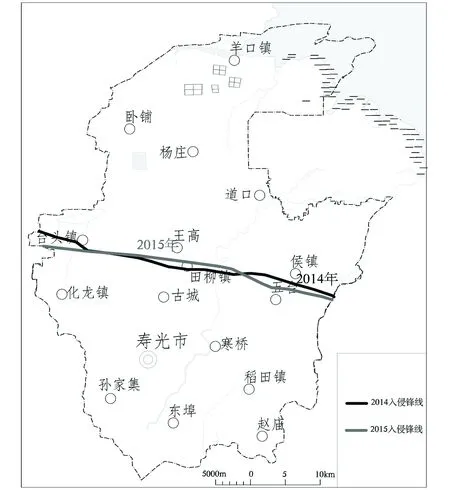
图3 2014年、2015年入侵锋线对比图

3 结论

海(咸)水入侵从发生和发展，地下水中的化学离子存在着迁移、吸附和汇集的过程，并且表现出一定的规律性。目前尚没有统一的监测指标，用的较多的为单指标评价。但是，由于区域水文地质条件的复杂性及人类活动的影响，单凭单一指标评判是不全面的，实际中往往产生偏差。而通过建立模糊数学模型综合评判方法，突出主要因素，兼顾其他次要因素，合理选择评价指标，正确赋予各因子权重，其评价结果能够较好的反映客观实际,方法简便、易操作。模糊数学模型综合评判方法是区域海(咸)水入侵程度和等级评价较为理想的评价方法。

[1] 刘宏伟,马震,陈社明,等.基于水化学与地球物理法的莱州湾南岸海(咸)水入侵勘查[J].现代地质,2015,29(2):337-343.

[2] 孙宗勋,陈军,谢强.珠江口西岸海水入侵现象调查分析[J].环境科学技术,2011,34(8):81-84.

[3] 涂向阳,高学平.模糊数学在海水入侵地下水水质评价中的应用[J].水利学报,2003,(8):64-69.

[4] 苗青,陈广泉,刘文全,等.莱州湾地区海水入侵灾害演化过程及成因[J].海岸工程,2013,32(2):69-78.

[5] 蒙永辉,傅建,王志成,等.潍坊北部海咸水入侵特征及现状评价[J].山东国土资源,2014,30(6):62-66.

[6] 孙晓明,徐建国,杨齐青,等.环渤海地区海(咸)水入侵特征与防治对策[J].地质调查与研究,2006,29(3):203-211.

[7] 刘桂仪.莱州湾南岸海咸水入侵的原因分析及防治对策[J].中国地质灾害与防治学报,2000,2(11)：1-4.

[8] 韩美.莱州湾地区海水入侵与地貌的关系[J].海洋与湖沼,1996,27(4):414-420.

[9] 刘宏伟,陈社明,郭旭,等.潍北平原海(咸)水入侵现状评价[J].地质科技情报,2017,36(1):213-218.

[10] 章斌,宋献方,韩冬梅,等.运用数理统计和模糊数学评价秦皇岛洋戴河平原的海(咸)水入侵程度[J].地理科学,2013,33(3):342-348.

[11] 茹湘兰.地下水污染的早期指示:以海水入侵为例[J].地质科技动态,1998,(11)：12-14.

[12] 俞仁培,杨道平,石万普.土壤碱化及其防治[M].北京:农业出版社,1984.

[13] 中国地质调查局.水文地质手册(第二版)[M].北京：地质出版社,2012.

[14] 乔吉果,龙江平,许冬,等.基于模糊数学的长江三角洲滨海地区海(咸)水入侵现状评价[J].海洋学研究,2011,29(4):57-64.

[15] 赵建.海水入侵水化学指标及侵染程度评价研究[J].地理科学,1998,18(1)：16-24.

[16] 熊德国,鲜学福.模糊综合评价方法的改进[J].重庆大学学报,2003,26(6):93-95.

Application of Fuzzy Mathematics in Water Quality Evaluation the Sea (salty) Water Intrusion——Taking Shouguang Area as an Example

FU Enguang1, WU Guangwei2, LI Tongxin3

(1. Shouguang Bureau of Land and Resources, Shandong Shouguang 262700, China; 2. Shandong Monitoring Station of Geological Environment, Shandong Jinan 250014, China; 3. Shandong Cartographic Institute, Shandong Jinan 250014, China)

According to the theory of fuzzy mathematics method, combinING with the characteristics of sea (saline) water intrusion, on the basis of groundwater quality monitoring results in Shouguang area flood period in 2015 , selecting four water chemical indicators as evaluation indexes, such as Cl-, mineralization degree, salty coefficient and sodium adsorption ratio, the fuzzy mathematics comprehensive evaluation model has been set up. Present situation of water and sea (salt) intrusion in Shouguang area has been evaluated, and the reliability of the fuzzy comprehensive evaluation results has been identified.

Sea water intrusion; fuzzy mathematics; water quality evaluation; comprehensive evaluation; Shouguang area

2016-11-16；

2017-04-11；编辑：陶卫卫

山东省寿光市海(咸)水入侵调查与自动化监测技术研究

付恩光 (1969—)，男，山东寿光人，工程师，主要从事水文地质、环境地质及管理工作；E-mail:sgkczy@163.com

付恩光,吴光伟，李同心.模糊数学在海(咸)水入侵水质评价中的应用——以寿光地区为例[J].山东国土资源，2017,33(7)：66-70.FU Enguang, WU Guangwei, LI Tongxin.Application of Fuzzy Mathematics in Water Quality Evaluation the Sea (salty) Water Intrusion——Taking Shouguang Area as an Example[J].Shandong Land and Resources, 2017,33(7)：66-70.

X824

B