用对立统一的眼光看“方法的方法”

郜舒竹

【摘 要】研究解决问题的一个重要课题就是“方法是从哪里来的？”这种“元方法”的思考中蕴含着辩证唯物主义对立统一的思想。运用这样的思想，思考问题中诸如多与少、乱与齐、局部与整体、动态与静态的矛盾，并将其相互转化，就可以得到解决问题的方法。

【关键词】辩证唯物主义 解题方法 数学课程 对立统一

数学课程内容作为千百年来人类智慧的结晶，其中必然蕴含着大量人类富于智慧的思想，在数学教学研究中挖掘这样的思想，并将其融入到教学与学习活动的设计中，无疑是体现数学课程内容人文性的重要方面。

比如，研究解决问题的一个重要课题就是“方法是从哪里来的？”数学教师经常会教导学生“要掌握方法”，但又很难说清楚“方法的来源”是什么，这种对于“方法的方法”的思考可以叫作“元方法（Meta-method）”的思考。如果把“学会学习”视为教育教学的目标之一，那么让学生经历并体验“元方法”的思考，就应当成为数学教学的重要内容。

一个数学问题通常由问题的目标、问题的障碍和已知的信息构成。故此，问题解决实质上就是超越已知信息与问题目标之间的障碍，建立已知信息与问题目标之间联系的过程。

所谓“障碍”，往往产生于思维中某种矛盾的对立状态。辩证唯物主义关于对立统一的基本规律告诉我们，矛盾的双方在一定的条件下可以互相转化。因此，为了超越障碍，首先需要识别产生障碍的主要矛盾，并发现使得矛盾双方实现统一的条件。这样的思维方式应该成为思考解决问题方法的方法。

一、 多与少

一些数学问题呈现出研究对象“多”的特点，比如：在平面上画10条直线，每两条直线都不重合。那么最多可以形成多少个交点？缺少数学经验的小学生遇到这样一个问题时，通常都是在纸上尝试去画出10条直线，而后试图数出交点的个数，这样的做法很难得到正确答案，原因就是要数的交点太多。因此，“多”就成为解决这个问题的障碍。

事实上，如果只有2条直线或3条直线，一般都不会感觉困难。现在就出现了这样的现象，“少”就会，“多”就不会。因此，“多”与“少”的矛盾就成为产生这个问题障碍的基本矛盾。如何处理这一对矛盾就成为解决这个问题的关键。

鉴于矛盾的双方在一定的条件下可以互相转化的启示，因此应该去建构“多”与“少”的转化模式，借助这种模式的建构过程，就会得到解决问题的方法。

首先从最少的1条直线的情况入手，发现没有交点。

再考虑2条直线的情况，由于问题的已知信息要求“每两条直线都不重合”，所以这2条直线的位置关系有两种，一种是平行，另一种是相交。而平行的情况没有交点，不符合已知信息中的“最多”。所以，2条直线的情况最多形成1个交点。

对于3条直线的情况，为了使得这种情况与前面的情况紧密联系，应该把3条直线的情况看作在2条直线的基础上添加1条直线。依据前面的启发，第三条直线不能与前面的任何一条直线平行。即使如此，第三条直线的添加还会出现两种情况，一种是经过前面2条直线的交点[见图1（a）]，另一种是不经过前面2条直线的交点[见图1（b）]。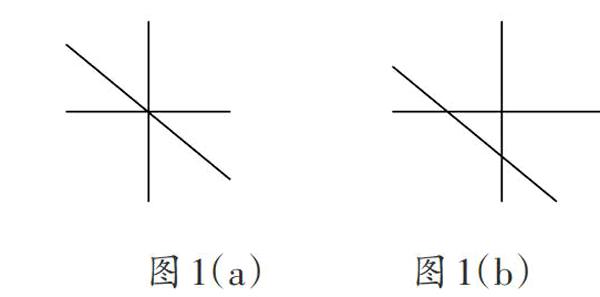

显然，为了使得交点个数最多，第三条直线不能够经过前面2条直线的交点。这样就可以知道，第三条直线与前面2条直线各有1个交点，所以3条直线的情况最多形成（1+2）=3个交点。

至此，已经可以归纳出新的已知信息。为了满足交点个数最多，所画的直线必须符合如下两个条件：

l 每2条直线不能平行。

l 每3条直线不能共点。

现在已经建构出了联系“多”与“少”的模式，这一模式可以从下表中清晰地看出来。

解决这个问题所用到的方法，可以称之为“从特殊到一般”或“难的不会，想简单的”的方法。其实，它的思想基础就是用辩证唯物主义对立统一的观点处理诸如“多”与“少”“大”与“小”“远”与“近”这样的矛盾。

因此就可以归纳出一种思考问题解决的方法，可以称之为“多的不会，想少的”，这也是辩证唯物主义方法论中“化难为易”的具體体现。

二、 乱与齐

数学中的一些问题还可能表现为研究对象的“乱”，比如：两位数中十位数字大于个位数字的数共有多少个？

随意列举一些满足问题要求的两位数并不困难，比如32，96，74等。但要数出准确的个数，并非轻而易举的。如果要数出全体两位数的个数，并不会感觉困难，而满足问题要求的两位数的个数肯定少于全体两位数的个数，为什么对象少了反而感觉困难了呢？这说明问题的主要障碍不在于“多”。更主要的原因是这些两位数在思维中的状态是“混乱”的，这才是问题的主要障碍。

“混乱”的对立一方应该是“整齐”。所以产生这个问题障碍的主要矛盾就应该是“混乱”与“整齐”的对立。如何把“混乱”的状态转化为“整齐”的状态，形成矛盾双方的统一，就成为解决这个问题的关键。

所谓“整齐”具有两方面的含义，一是“类属明确”，二是“排列有序”。好比日常生活中收拾房间时所做的“书进书柜、衣入衣柜”等，而且书在书柜中不能胡乱堆放，衣在衣柜中不能放得乱七八糟，而应该有序排列。因此，解决这个问题的过程实际上就是把十位数字大于个位数字的两位数按照某种规则“分类、排序”。

“分类、排序”也是一种模式的建构，是抽象思维的产物。凡抽象思维的产物就具有一定的“自由度”，表现出来的是模式的多样性。比如关于十位数字大于个位数字的两位数的分类与排序，可以建构出如下不同的模式。

模式一

[十位数字 十位数字大于个位数字的两位数 个数 1 10 1 2 20，21 2 3 30，31，32 3 4 40，41，42，43 4 5 50，51，52，53，54 5 6 60，61，62，63，64，65 6 7 70，71，72，73，74，75，76 7 8 80，81，82，83，84，85，86，87 8 9 90，91，92，93，94，95，96，97，98 9 合计 45 ]

模式二

[个位数字 十位数字大于个位数字的两位数 个数 0 10，20，30，40，50，60，70，80，90 9 1 21，31，41，51，61，71，81，91 8 2 32，42，52，62，72，82，92 7 3 43，53，63，73，83，93 6 4 54，64，74，84，94 5 5 65，75，85，95 4 6 76，86，96 3 7 87，97 2 8 98 1 合计 45 ]

模式一的分类依据是“十位数字相同归为同一类”，模式二的分类依据是“个位数字相同归为同一类”。所有的排序都依据“从小到大”。可以概括地说，“分类与排序”是对“整齐模式”的建构。模式虽然不同，但“整齐”的效果是一致的。由此就可以得到一种思考问题的方法，不妨叫作“变乱为齐”。

三、 局部与整体

先看一个例子：如图2， ABC是任意一个三角形，D是AB边上的中点，E是BC边上的中点。连接CD和AE两条线段，将三角形ABC分为了四个部分。如果假设三角形ABC的面积为1，那么这四个部分的面积分别是多少？

把整个三角形ABC看作一个整体，那么三角形ACO、三角形ADO、三角形CEO和四边形BEOD就是相对于这一整体的四个局部。学习数学过程中习惯的问题是已知局部求整体，而这个问题恰好是反过来，是已知整体求局部的问题。

在一般情况下，局部一旦确定，则整体也就随之确定。反过来，整体确定，局部却未必确定。这个问题恰恰就是“已知整体求局部”，因此问题的思维障碍就在于这种“不确定”。产生障碍的基本矛盾自然就是“整体”与“局部”的对立。解决问题的关键就在于统一整体与局部之间的矛盾，这种统一依赖于二者之间的数量关系。

所谓“不确定”体现的是一种动态，而制约这种动态的基本元素就是D点和E点的位置，这两个点的位置一旦确定，这种动态就转变为静态了。问题的已知信息告诉我们，D点和E点分别是所在边上的中点，从而四个局部之间的关系也就确定了，要想发现局部与整体之间的数量关系，应该从发现局部与局部之间的关系入手。

首先不难看出，整个三角形图形中有4个面积为三角形ABC面积[12]的三角形，分别是三角形ACD、CDB、ACE和AEB。由于三角形AEB和CDB的面积都是[12]，同时去掉它们的公共部分ODBE就可以知道三角形OCE和AOD的面积相等。这时的关键问题在于建立四边形ODBE与这两个三角形之间的关系，可以连接OB画出一条辅助线，见图3。

利用 “等底等高的三角形面积相等”这一结论，立刻知道三角形AOD和OBD面积相等，三角形OCE和OEB面积相等。又由于三角形OCE和AOD面积相等，所以AOD、OBD、OEB和OCE这4个三角形面积相等，而且其中3个三角形的面积之和为原三角形ABC的[12]，因此现在就可以求出三角形AOD和OCE的面积分别为：

[12÷3=16]

四边形ODBE的面积为：

[16×2=3]

进而就可以求出三角形ACO的面积为：

1[-16×2-13=13]

至此四个部分的面积就都求出来了。

关于“局部”与“整体”之间的矛盾，在不同领域可以有不同的意义。这个问题中反映出来的实际上是“动态”与“静态”之间的对立统一。

四、 动态与静态

日常生活中开玩笑的时候，形容一个长着“八字眉”的人的眉毛就像“8点20分”一样（见图4）。

这是非常形象的描述，但仔细想一想会发现，这个形容并不精确。事实上，用钟表上的时针和分针描述“八字眉”时，时针与分针应该处于对称位置（见图5）。

也就是说，两针应该以钟表上“6”和“12”两点的连线为对称轴。而“8点20分”时分针指向“4”，时针指向“8”与“9”之间距“8”的三分之一处，这时显然两针并不处于对称位置（见图6）。

日常语言描述“八字眉”的不精确，促使人产生了解“八字眉”到底应该是8点多少分的欲望。因此“问题”就产生了。用数学的语言叙述这个问题就是：8点多少分时，时针与分针关于“6”与“12”的连线对称？

钟表是描述时间的工具，时间的“动态”是永恒的。钟表上所谓“八字眉”的状态是一种“静态”。而这种静态的时刻，直观上又不能準确地确定。因此需要把 “静态”融入到“动态”之中，实现二者的统一。

时间的动态，在钟表上反映出来的是指针的运动。所谓“八字眉”的静态实质上就是指针运动过程中的一个“瞬间”。时间的动态无始无终，因此需要截取一个时间段，也就是规定两个“瞬间”分别作为时间段的“起点”和“终点”。当然，这个时间段的截取有一定的随意性，需要考虑怎样截取有益于问题的解决。

如果把8点整作为“起点”，把“八字眉”的时刻作为“终点”，那么问题就变成了从起点到终点经过了多少分钟？这样就把时间的“动态”与“八字眉”的“静态”有机地联系起来了。

为了借助“行程问题”的解决方法，就需要“路程”和“速度”这样的量，前提是需要有“路程单位”。比如，可以规定时针1小时转过的1格为1个路程单位，这样，时针的转动速度就是每分钟[160]格，分针的转动速度是每分钟[15]格。

直观上不难看出，“八字眉”的时刻应该是8点15分至8点20分之间。所谓时针与分针处于对称位置，实际上就是8点多钟的某一时刻，时针、分针所指向的位置与钟表上数字“6”所在位置的距离相等。

从8点整开始想，时针指向“8”，分针指向“12”，假设从这时到两针所指位置与数字“6”的位置距离相等用了x分钟，分别将时针与分针过x分钟后与数字“6”的距离表示出来，就可以列出如下方程：

2+[x60]=6-[x5]

解方程得：x=[18613]

因为两针与“6”的距离相等，也就是与“12”的位置距离相等，所以还可以分别将两针经过x分钟后与“12”的距离以列方程的形式表示出来：

4-[x60=][x5]

同样可以解得：x=[18613]

最后需要说明，虽然通过识别问题的障碍进行矛盾分析是发现解决问题方法的有效途径，但由于问题的障碍具有相对性，也即面对同样的问题或不同的问题解决者，问题的障碍可能是不同的，所以问题解决的矛盾分析具有相当的复杂性。

（首都师范大学初等教育学院 100048）